Perspectives on Differential Privacy
From Online Learning to Hypothesis Testing
Victor Sanches Portella
July 2023
cs.ubc.ca/~victorsp
Thesis Proposal Defense
Previous Work
Online Optimization and Stochastic Calculus
Stabilized OMD
ICML 2020, JMLR 2022
Relative Lipschitz OL
NeurIPS 2020
Fixed time 2 experts
ALT 2022
p_t
1 - p_t
Continuous time \(n\) experts
Under review - JMLR
Online Optimization and Stochastic Calculus
Preconditioner Search for Gradient Descent
Under review - NeurIPS 2023
Online Learning
Differential Privacy
Probability Theory
Expected Norm of continuous martingales
\displaystyle \sup_{\tau} \frac{\mathbf{E}[\lVert X_{\tau} \rVert_{\infty}]}{\mathbf{E}[\sqrt{\tau}]}
Under review - Stoc. Proc. & App.
Feedback and Suggestion Welcome!
Unbiased DP Mechanisms
Positive Definite Mechanisms
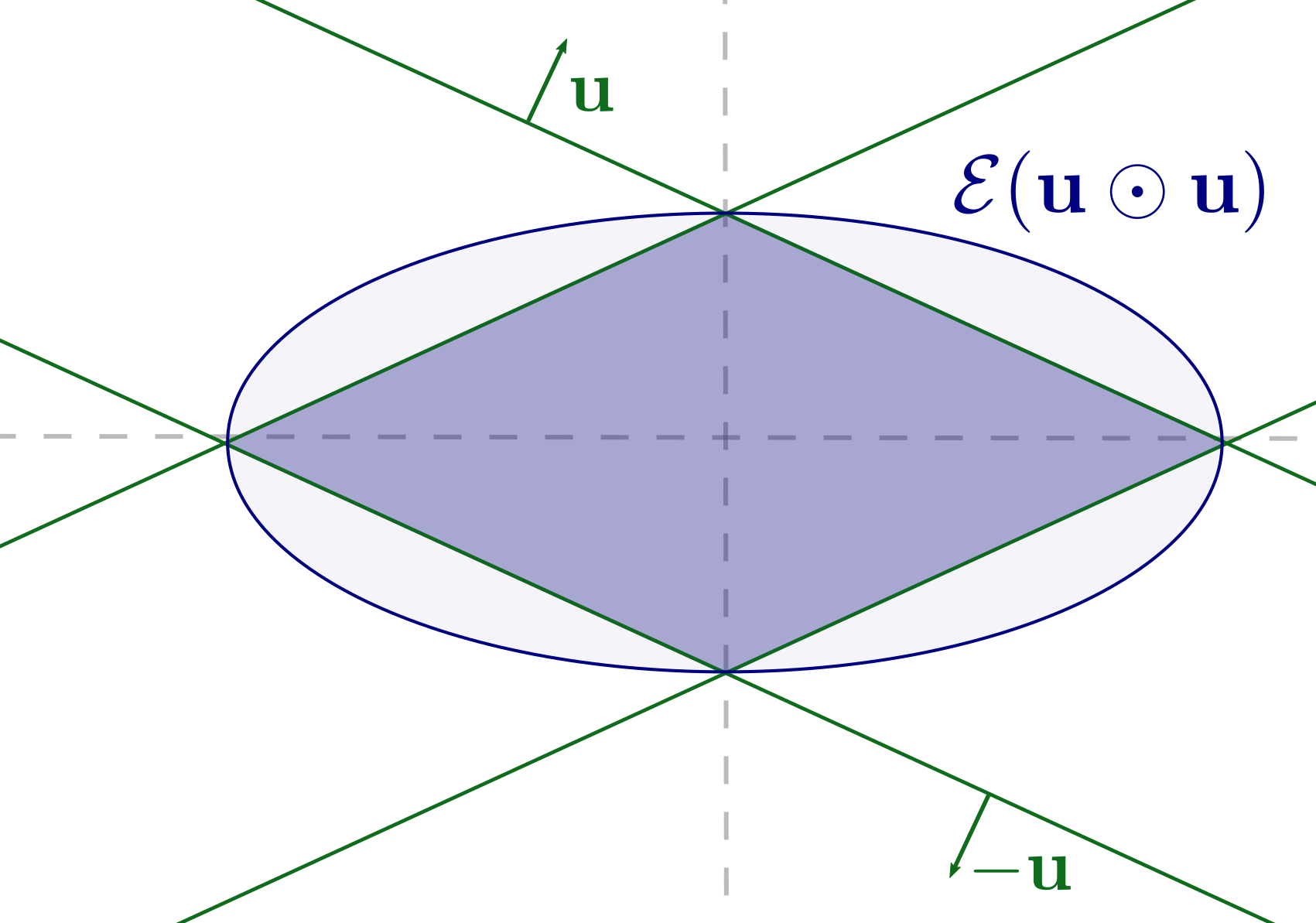
Goal: release the following query with differential privacy
\displaystyle
x_i \in \mathbb{R}^d~\text{with}~\lVert x_i\rVert_2 \leq 1
Classical Solution:
but we may have \(\mathcal{M}(x) \not\succeq 0\)
We had
\displaystyle
Q(x) \succeq 0
\displaystyle
\mathcal{M}(x) = Q(x) + (G + G^T)
Question: Can we have \(\mathcal{M}(x) \succeq 0\) while being DP in a more "natural" way?
We can truncate the eigenvalues (post-processing of DP)
\displaystyle
Q(x) = \frac{1}{n} \sum_{i = 1}^n x_i x_i^{T}
Gaussian Mechanism (similar to vector case)
1D Case - Positive Mechanisms
1D Case:
\displaystyle
q(x) = \frac{1}{n} \sum_{i = 1}^n x_i
DP Mechanism
\displaystyle
x_i \in [1,2]~\text{for each}~i
\displaystyle
\mathcal{M}(x) = q(x) + Z
Gaussian or Laplace noise
Making it positive:
\displaystyle
\mathbf{E}\big[[\mathcal{M}(x)]_+\big] \neq q(x)
Question: Can we have \(\mathcal{M}(x)\) DP, non-negative, and unbiased?
Noise with Bounded Support
\displaystyle
\mathcal{M}(x) = q(x) + Z
Idea: Use \(Z\) with bounded support
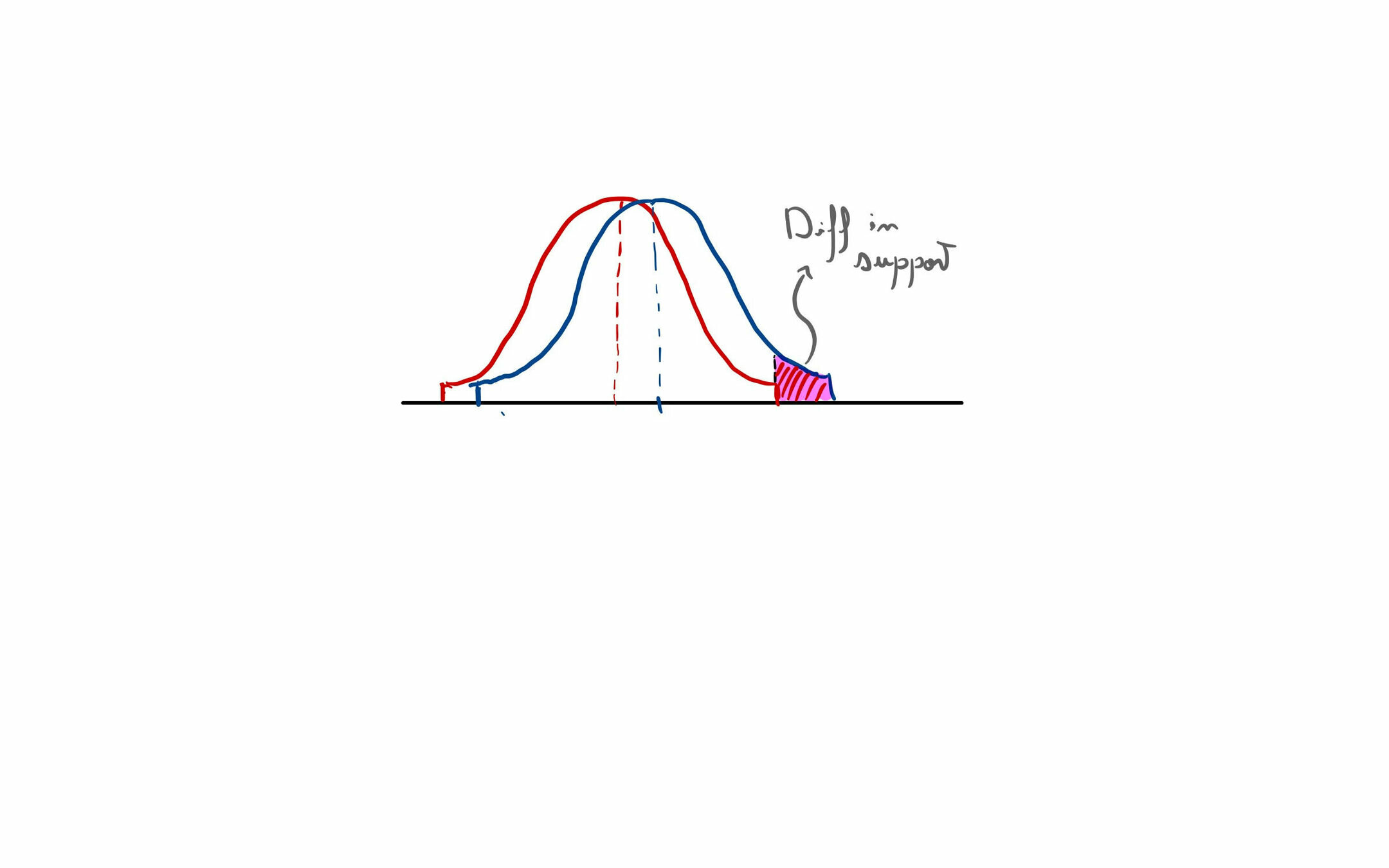
Approach 1: Design continuous densities that go to 0 at boundary
Simple proof, noise with width \( \approx \ln (1/\delta)/\varepsilon\)
Approach 2: Truncate Gaussian/Laplace density
We have general conditions for a density to work
Noise width needs to be \(\gtrsim \ln(1/\delta)/\varepsilon\)
Can compose better
Dagan and Kur (2021)
\Bigg\}
Unbiased and non-negative if \(q(x)\) far from 0
Back to the Matrix Case
\displaystyle \mathcal{E} = \Big\{\lambda_{\min}(G + G^T) \gtrsim \frac{\sqrt{d \ln(1/\delta)}}{\varepsilon} + \frac{\ln(1/\delta)}{\varepsilon}\Big\}.
Large probability of \(\mathcal{E}\) comes from random matrix theory
Similar argument is also used to argue about error in the Gaussian mechanism for matrices.
Is the error optimal?
Proposition: \(\mathcal{M}\) is \((\varepsilon, \delta)\)-DP and \(\mathcal{E}\) an event on the rand. of \(\mathcal{M}\).
\(\mathbf{P}(\mathcal{E}) \geq 1 - \delta \implies \) \(\mathcal{M}\) conditioned on \(\mathcal{E}\) is \((\varepsilon, 4 \delta)\)-DP
Error for DP Covariance Matrix Estimation
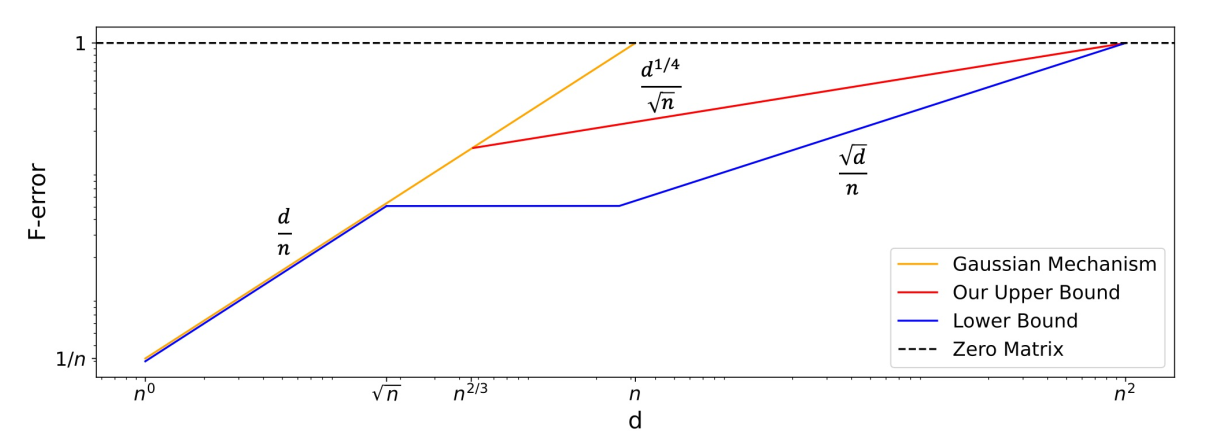
Dong, Liang,Yi, "Differentially Private Covariance Revisited" (2022).
Project idea: Work on closing the gap in error for \(\sqrt{n} \lesssim d \lesssim n^2\)
Pontentially related to work on Gaussian Mixture Models by Nick and co-authors.
Hypothesis Testing View of DP
High-level idea of DP
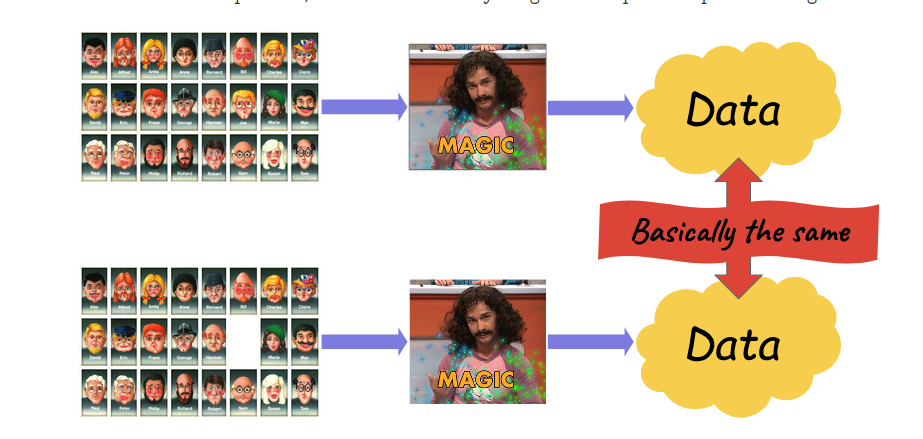
Ted's blog: https://desfontain.es/privacy/differential-privacy-in-more-detail.html
The Definition of DP and Its Interpretation
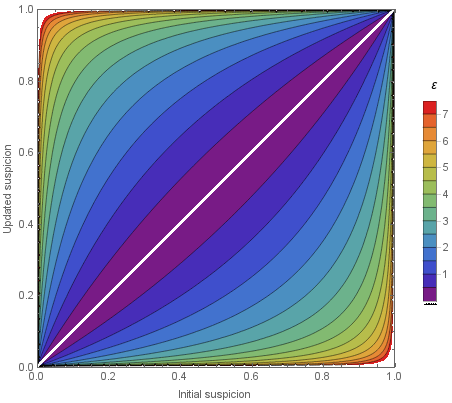
Definition of Approximate Differential Privacy
\mathbf{P}(\mathcal{M(x)} \in S) \leq e^{\varepsilon} \cdot
\mathbf{P}(\mathcal{M(x')} \in S) + \delta
We have \(e^\varepsilon \approx 1 + \varepsilon\) for small \(\varepsilon\)
A curve \((\varepsilon, \delta(\varepsilon))\) provides a more detailed description of privacy loss
"neighboring"
Hard to interpret
Pointwise composition
It is common to use \(\varepsilon \in [2,10]\)
The Definition of DP and Its Interpretation
Hypothesis Testing Definition
or
x
x'
\displaystyle \mathcal{M}
s
Output
Null Hypothesis
Alternate Hypothesis
H_0
H_1
With access to \(s\) and \(\mathcal{M}\), decide whether we are on \(H_0\) on \(H_1\)
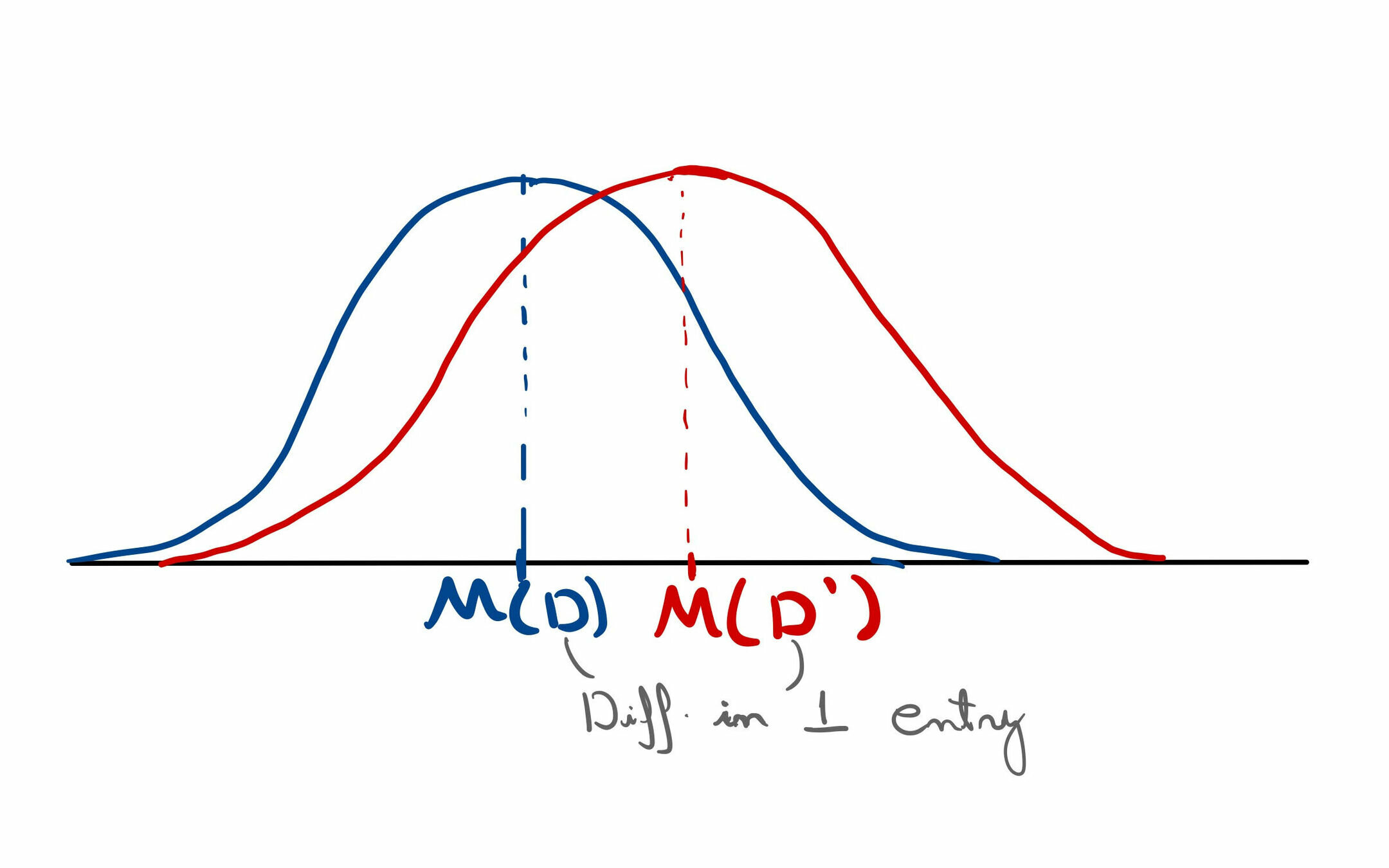
Statistical test:
False Negative rate
False Positive rate
\displaystyle \phi(s) =
\begin{cases}
1 & \text{if believes}~H_0\\
0 & \text{if believes}~H_1
\end{cases}
\mathrm{FN}(\phi) =
\mathrm{FP}(\phi) =
Trade-off Function
Statistical test:
False Negative rate
False Positive rate
\displaystyle \phi(s) =
\begin{cases}
1 & \text{if believes}~H_0\\
0 & \text{if believes}~H_1
\end{cases}
\mathrm{FN}(\phi) =
\mathrm{FP}(\phi) =
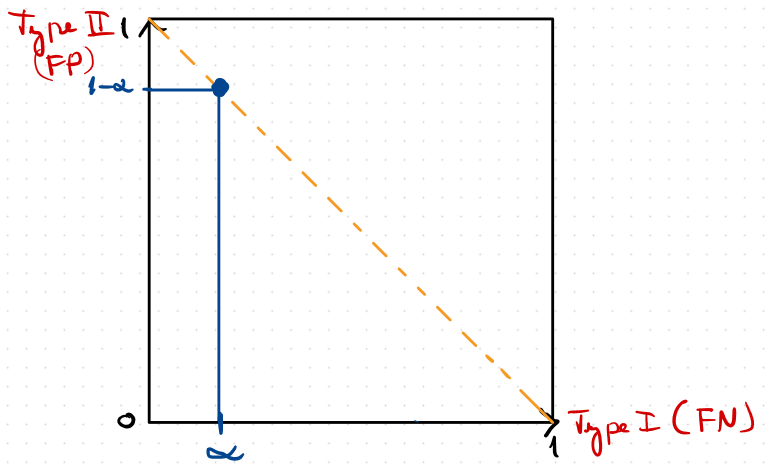
Trade-off function
\displaystyle T(\mathcal{M}(x), \mathcal{M}(x'))(\alpha) = \inf_{\phi}\{\mathrm{FP}(\phi) \colon \mathrm{FN}(\phi) \leq \alpha\}
Hypothesis Testing Definition
\(f\)-DP:
\displaystyle f(\alpha) \leq T(\mathcal{M}(x), \mathcal{M}(x'))(\alpha)
for all neigh.
x,x'
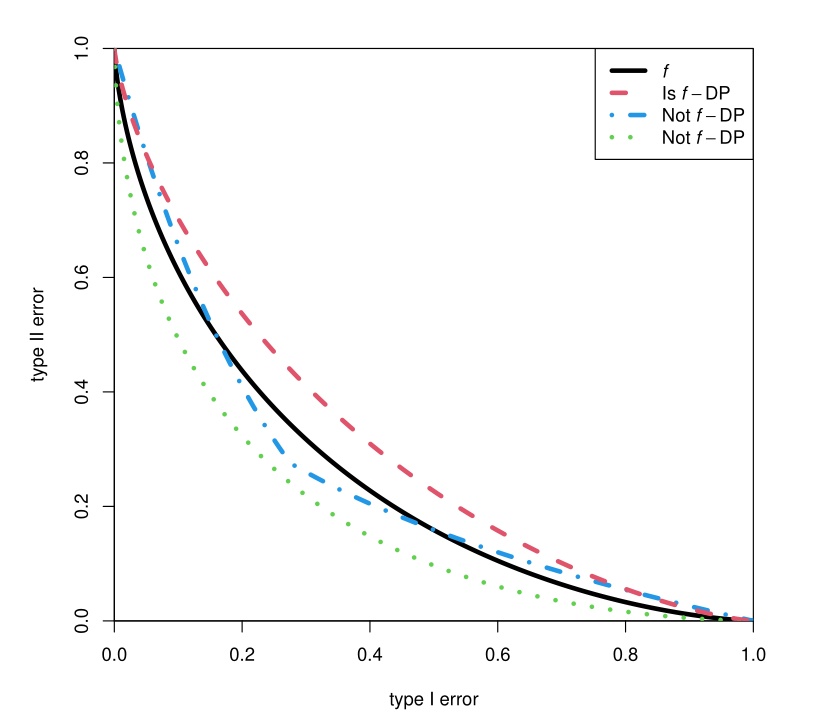
FP
FN
Composition of \(f\)-DP
Composition of a \(f\)-DP and a \(g\)-DP mechanism
f = T(\mathcal{N}(0,1) , \mathcal{N}(\mu_1, 1))
g = T(\mathcal{N}(0,1) , \mathcal{N}(\mu_2, 1))
f \otimes g = T\big(\mathcal{N}(0,I) , \mathcal{N}((\mu_1, \mu_2), I)\big)
= T\big(\mathcal{N}(0,1) , \mathcal{N}(\sqrt{\mu_1^2 + \mu_2^2}, 1)\big)
Product distributions
Example: Composition of Gaussian mechanism
f \otimes g = T(P_f \times P_g, Q_f \times Q_g)
f = T(P_f , Q_f)
g = T(P_g, Q_g)
where
\displaystyle \Bigg\{
Composition of \(f\)-DP - Central Limit Theorem
Central Limit Theorem for \(f\)-DP composition
f_1 \otimes f_2 \otimes \cdots \otimes f_n \approx T(\mathcal{N}(0,1), \mathcal{N}(\mu, 1))
Berry-Essen gives a \(O(1/\sqrt{n})\) convergence rate
Dong et al. give a \(O(1/n)\) convergence rate when each \(f_i\) is pure DP
Simpler composition for mixture of Gaussian and Laplace?
Can knowledge of the mechanism (e.g., i.i.d. noise) help with composition?
CLT is too general
Project idea: Analyze composition of \(f\)-DP beyond CLT arguments
Hypothesis Testing Tools and Semantics
Project idea: Use hypothesis testing tools to better understand low-privacy regime
What is the meaning of \((\varepsilon, \delta)\)-DP for large values of \(\varepsilon\)?
There are DP algorithms with large \(\varepsilon\) that are far from private
Per-attribute DP gives a white-box view of DP
Not clear how it would work in ML
A curve of \((\varepsilon, \delta(\varepsilon))\)-DP guarantees sometimes helps
Renyi DP, zero Concentrated DP
Beyond membership inference
Online Learning Meets DP
Connections Between DP and OL
Online Learning and PAC DP Learning are equivalent
Online Learning algorithms used in DP
Differentially Private Online Learning
Differentially Private lens of Online Learning
Several connections between
Differential Privacy and Online Learning
Differentially Private Online Learning
\ell_1, \ell_2, \dotsc, \ell_t, \dotsc, \ell_T
\ell_1, \ell_2, \dotsc, \ell_t', \dotsc, \ell_T
or
DP OL Algorithm
DP OL Algorithm
Shoul be "basically the same"
Project Idea:
Unified algorithm for adaptive & oblivious cases
Lower-bounds for \(d \leq T\)
Optimal DP algorithm with few experts
Differential Privacy Lens of Online Learning
DP can be seen as a form of algorithm stability
Analysis of Follow the Perturbed Leader (Abernethy et al. 2019)
There are connections of FTPL to convex duality, but via smoothing
\displaystyle x_t = \mathrm{arg~min} \sum_{s < t }\ell_s(x) + \langle x, \mathbf{p} \rangle
x
Random linear perturbation
Project idea: Further connect FTPL and DP lens with convex duality
Project Assesment
Project Assesment
DP Covariance Estimation
Study of composition of \(f\)-DP
Semantics of DP in the "low-privacy regime"
Online Learning analysis via DP lens
DP Online Learning
Personal Interest
Uncertainty
Backup Slides
Positive Average of Positive Numbers
Standard Approach:
\displaystyle
\mathcal{M}(D) = \frac{1}{n} \sum_{i = 1}^n x_i + Z
Always Positive Version:
\displaystyle
\mathcal{M}'(D) = \Big[\mathcal{M}'(D)\Big]_+
Biased
Still DP
Question: Are there positive unbiased DP algorithms?
Assumption: True average is bounded away from 0
Differentially Private Online Learning
Follow the Regularized Leader vs Switching cost
Lower-bounds for adaptive adversaries (\(d > T\))
\displaystyle \Bigg \{
Linear regret if \(\varepsilon < 1/\sqrt{T}\) and \(\delta > 0\)
Linear regret if \(\varepsilon < 1/10\) and \(\delta = 0\)
Project Idea:
Unified algorithm for adaptive & oblivious cases
Lower-bounds for \(d \leq T\)
Optimal DP algorithm with few experts
\ell_1, \ell_2, \dotsc, \ell_t, \dotsc, \ell_T
\ell_1, \ell_2, \dotsc, \ell_t', \dotsc, \ell_T
or
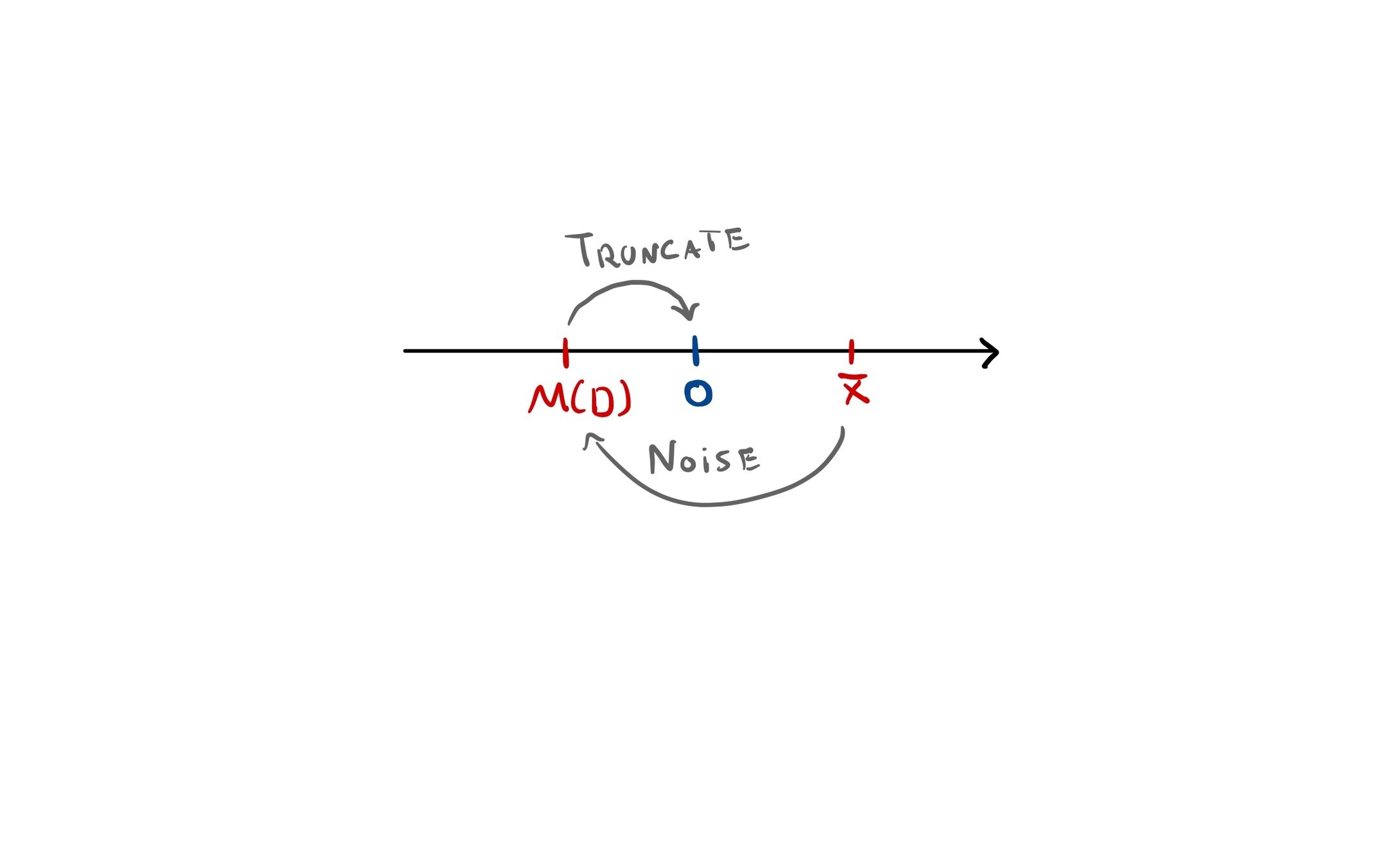
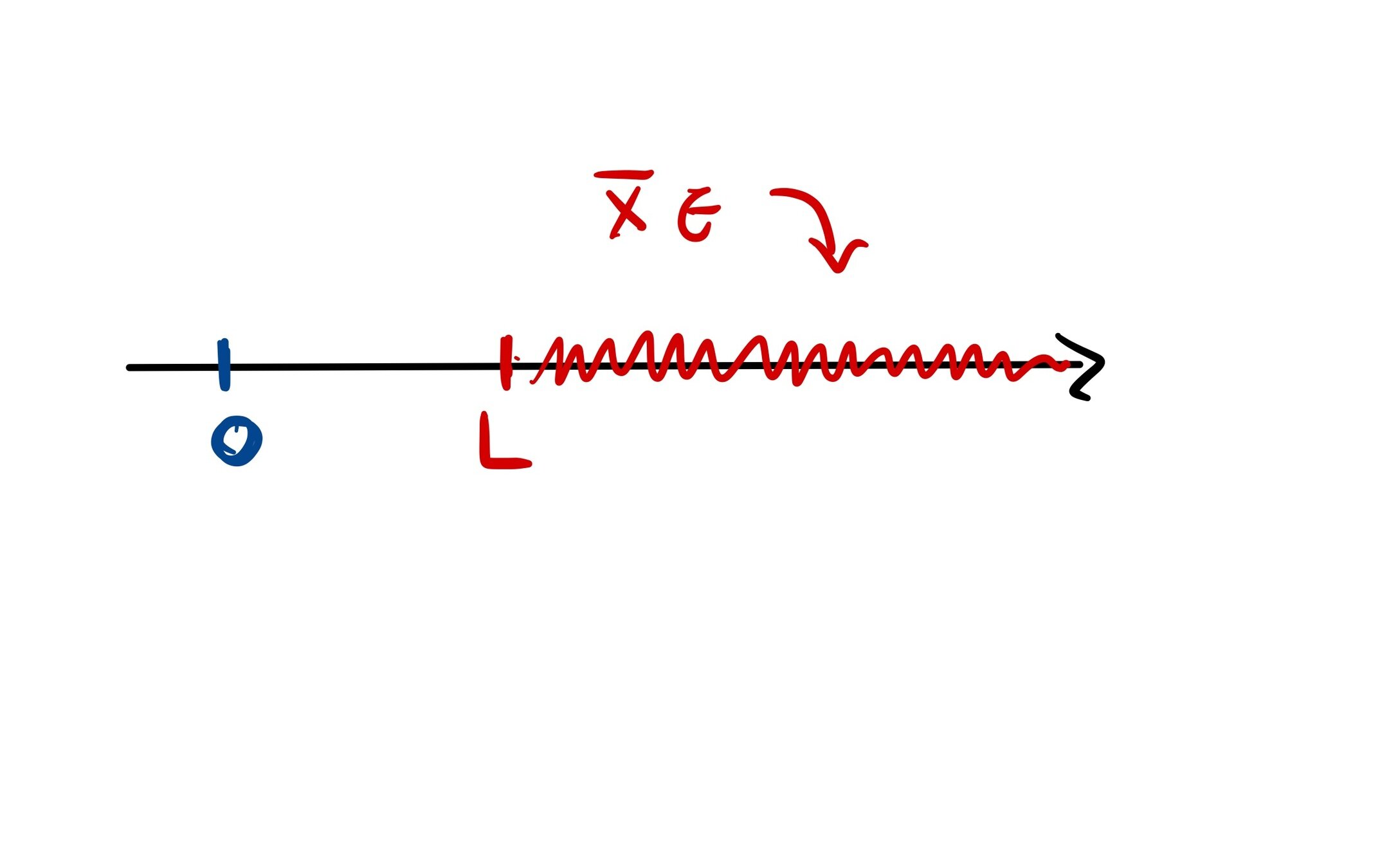
The Effect of Truncation on Bias
"Differential Privacy and Fairness in Decisions and Learning Tasks: A Survey", 2022, Fioretto et al.
More Details in Case There is Time
\displaystyle
Z
\displaystyle
\eta \cdot
g(z)
with density
Density on \([-1,1]\)
Noise scale
\(g\) symmetric \(\implies\) unbiased
Thesis Proposal Defense
By Victor Sanches Portella
