Searching for
Optimal Per-Coordinate Step-sizes with
Frederik Kunstner, Victor S. Portella, Nick Harvey, and Mark Schmidt
Multidimensional Backtracking
Adaptive algorithms in optimizaton
"Adaptive" step-sizes for each parameter
One formal definition from Online Learning (AdaGrad)
Hypergradient
Adam, RMSProp, RProp
Aprox. 2nd Order Methods
Designed for adversarial and non-smooth optimization
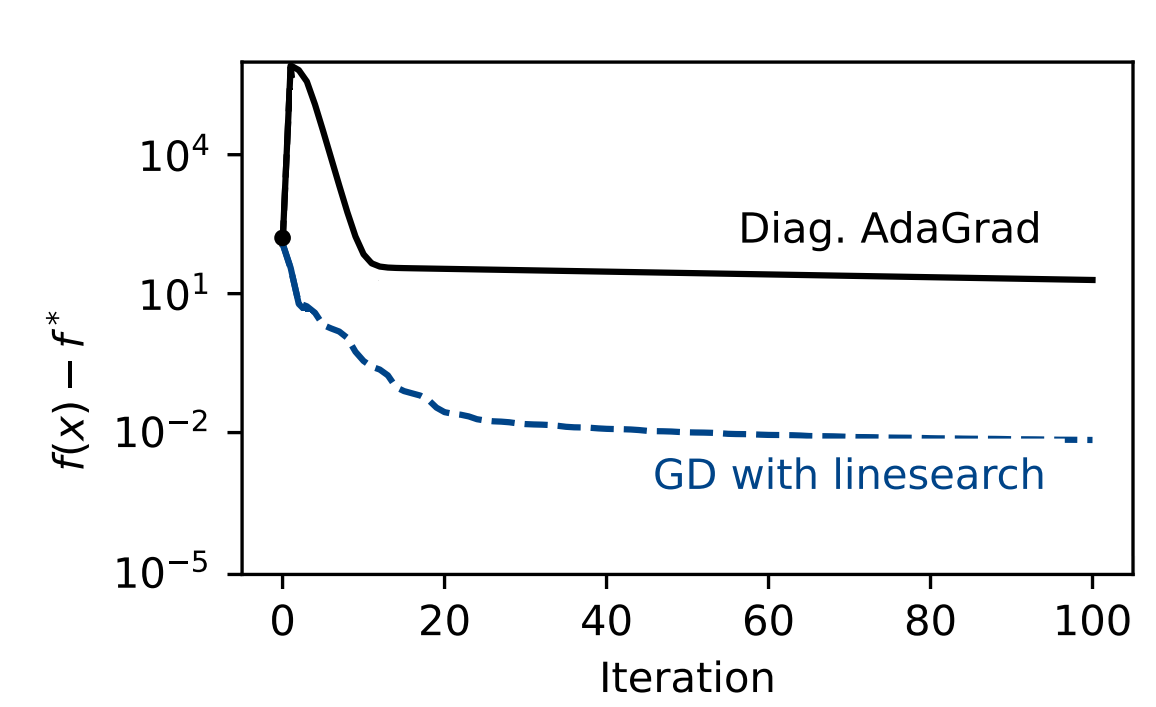
Classical line-search is better in simpler problems
But what does adaptive mean?
Definition of an Optimal Preconditioner
\displaystyle \kappa(\nabla^2 f(\mathbf{x})) \gg 1
\displaystyle \displaystyle \kappa(\mathbf{P}_*^{1/2} \nabla^2 f(\mathbf{x}) \mathbf{P}_*^{1/2}) = \kappa_*
\displaystyle \kappa_*
\displaystyle f(\mathbf{x}_{t+1}) - f^* \leq \left( 1 - \frac{1}{\phantom{\kappa_{*}}}\right) (f(\mathbf{x}_t) - f^*)
\displaystyle \mathbf{x}_{t+1} = \mathbf{x}_t - \eta \nabla f(\mathbf{x}_t)
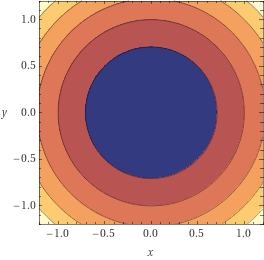
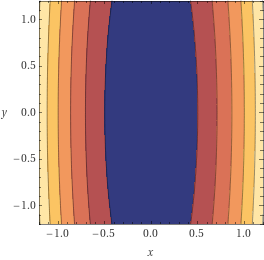
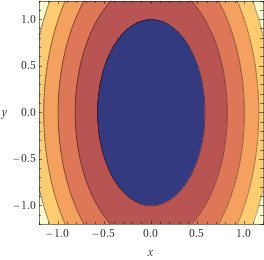
Adaptivity for
smooth
strongly convex
problems
\displaystyle \kappa(\mathbf{P}^{1/2} \nabla^2 f(\mathbf{x}) \mathbf{P}^{1/2}) > 1
\displaystyle \kappa_{\mathbf{P}}
\displaystyle f(\mathbf{x}_{t+1}) - f^* \leq \left( 1 - \frac{1}{\phantom{\kappa_{*}}}\right) (f(\mathbf{x}_t) - f^*)
\displaystyle \kappa_{}
\displaystyle f(\mathbf{x}_{t+1}) - f^* \leq \left( 1 - \frac{1}{\phantom{\kappa_{*}}}\right) (f(\mathbf{x}_t) - f^*)
Multidimensional Backtracking
\displaystyle f(\mathbf{x}_{t+1}) - f^* \leq \left( 1 - \frac{1}{\phantom{\color{red}\sqrt{2d}}} \frac{1}{\phantom{\color{blue}\kappa_{*}}}\right) (f(\mathbf{x}_t) - f^*)
\displaystyle \sqrt{2d}
\displaystyle \kappa_*
\displaystyle \mathbf{x}_{t+1} = \mathbf{x}_t - \phantom{\color{blue}\mathbf{P}_{\!*}} \nabla f(\mathbf{x}_t)
\displaystyle
{\mathbf{P}_{\!*}}
\displaystyle \mathbf{x}_{t+1} = \mathbf{x}_t - \phantom{\color{red}\mathbf{P}} \nabla f(\mathbf{x}_t)
\displaystyle {\mathbf{P}}
High level Idea
f(\mathbf{x}_t - \mathbf{P} \nabla f(\mathbf{x}_t))
\mathbf{x}_{t+1} = \mathbf{x}_t - \mathbf{P} \nabla f(\mathbf{x}_t)
In each iteration
If
If
makes
enough progress
Update \(\mathbf{x}\):
Else
Update \(\mathbf{P}\)
Classical Line Search
Backtracking line search
0
\alpha_{0}
\tfrac{\alpha_{0}}{2}
\mathrm{\alpha^*}
\tfrac{\alpha_{0}}{4}
\displaystyle f(\mathbf{x}_{t+1}) \leq f(\mathbf{x}_t) - \alpha \; \tfrac{1}{2} \lVert \nabla f(\mathbf{x}_t) \rVert_2^2
Armijo condition
\displaystyle \Big\{
Within a factor of 2
on
smooth functions
Diagonal Preconditioner Search
\displaystyle f(\mathbf{x}_{t+1}) \leq f(\mathbf{x}_t)
- \tfrac{1}{2} \lVert \nabla f(\mathbf{x}_t) \rVert_P^2
Armijo condition
Generalized
Set of Candidate
Preconditioners
\mathbf{P}
"Too Big"
Volume removed is exponentially small with dimension
Diagonal Preconditioner Search
\displaystyle f(\mathbf{x}_{t+1}) \leq f(\mathbf{x}_t)
- \tfrac{1}{2} \lVert \nabla f(\mathbf{x}_t) \rVert_P^2
Armijo condition
Generalized
\mathbf{P}
"Too Big"
Key idea: w.r.t. \(\mathbf{P}\) yields a
Hypergradient
separating hyperplane
Set of Candidate
Preconditioners
Cutting Planes Methods and Performance
Design efficient cutting plane methods that guarantee
\displaystyle f(\mathbf{x}_{t+1}) - f^* \leq \left( 1 - \frac{1}{\phantom{\color{red}\sqrt{2d}}} \frac{1}{\phantom{\color{blue}\kappa_{*}}}\right) (f(\mathbf{x}_t) - f^*)
\displaystyle \sqrt{2d}
\displaystyle \kappa_*
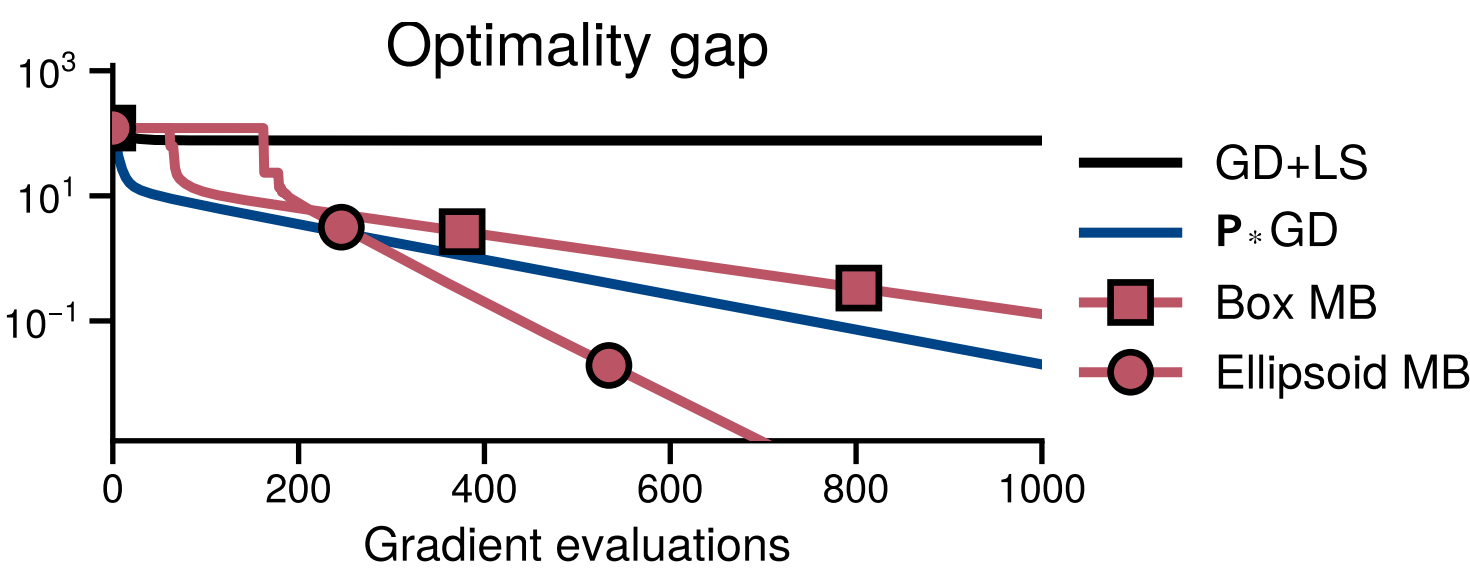
Cutting Planes Methods and Performance
Design efficient cutting plane methods that guarantee
\displaystyle f(\mathbf{x}_{t+1}) - f^*) \leq \left( 1 - \frac{1}{\phantom{\color{red}\sqrt{2d}}} \frac{1}{\phantom{\color{blue}\kappa_{*}}}\right) (f(\mathbf{x}_t) - f^*)
\displaystyle \sqrt{2d}
\displaystyle \kappa_*
Old Slides to the Right
Definition of an Optimal Preconditioner
Preconditioned Condition Number
\displaystyle \kappa_{*} =
\kappa(\mathbf{P}_*^{1/2} \nabla^2 f(\mathbf{x}) \mathbf{P}^{1/2})
\displaystyle \kappa_*
\displaystyle f(\mathbf{x}_{t+1}) - f(\mathbf{x}_t) \leq \left( 1 - \frac{1}{\phantom{\kappa_{*}}}\right) (f(\mathbf{x}_t) - f(\mathbf{x}_{t-1})
Definition of adaptivity for problems
smooth
strongly convex
\displaystyle \mathbf{x}_{t+1} = \mathbf{x}_t - \mathbf{P}_* \nabla f(\mathbf{x}_t)
Preconditioned GD
\displaystyle \kappa(\nabla^2 f(\mathbf{x})) \gg 1
\displaystyle \kappa(\nabla^2 f(\mathbf{x})) = 1
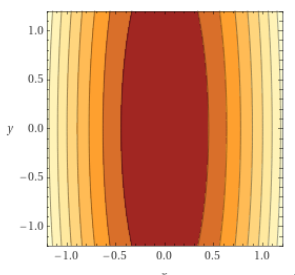
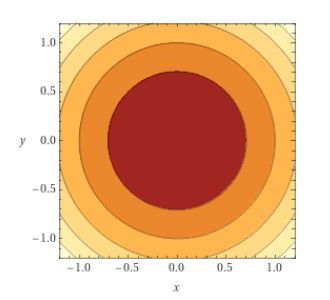
Condition Number
\displaystyle \kappa(\nabla^2 f(\mathbf{x}))
Diagonal Preconditioner Search
\displaystyle f(\mathbf{x}_{t+1}) \leq f(\mathbf{x}_t)
- \tfrac{1}{2} \lVert \nabla f(\mathbf{x}_t) \rVert_P^2
Armijo condition
Generalized
Set of Candidate
Preconditioners
\mathbf{P}
Gradient of
f(\mathbf{x}_{t+1}) - f(\mathbf{x}_t)
+ \tfrac{1}{2} \lVert \nabla f(\mathbf{x}_t) \rVert_P^2
\displaystyle h(\mathbf{P}) =
Use of Hypergradients with formal guarantees
Also Fail the Armijo Condition
Almost no overhead by exploiting symmetry
Adaptive First-Order Methods
Finding Good Step-Sizes on the Fly
\displaystyle \implies
f(x_t) - f(x_*) \displaystyle \lesssim \left( 1 - \frac{1}{\kappa} \right)^t
\displaystyle \alpha = \tfrac{1}{L}
\displaystyle \kappa = L/\mu
What if we don't know \(L\)?
Line-search!
"Halve your step-size if too big"
f(x_t) - f(x_*) \displaystyle \lesssim \left( 1 - \phantom{\frac{1}{2}} \cdot \frac{1}{\kappa} \right)^t
\displaystyle \frac{1}{2}
\(\mu\)-strongly convex
\(f\) is
\(L\)-smooth
and
\preceq \nabla^2 f(x) \preceq
L \cdot I
\mu \cdot I
"Easy to optimize"
x_{t+1} = x_t - \alpha \nabla f(x_t)
Gradient Descent
"Adaptive" Methods
We often can do better if we use a (diagonal) matrix preconditioner
x_{t+1} = x_t - \phantom{P} \nabla f(x_t)
P
x_{t+1} = x_t - \phantom{P} \nabla f(x_t)
We often can do better if we use a (diagonal)
(Quasi-)Newton Methods
Hypergradient Methods
Hyperparameter tuning as an opt problem
Unstable and no theory/guarantees
Online Learning
Formally adapts to adversarial and changing inputs
\displaystyle \Bigg \{
\displaystyle \Bigg \{
\displaystyle \Bigg \{
Super-linear convergence close to opt
What is a good \(P\)?
May need 2nd-order information.
Too conservative in this case (e.g., AdaGrad)
"Fixes" (e.g., Adam) have few guarantees
State of Affairs
"AdaGrad inspired an incredible number of clones, most of them with similar, worse, or no regret guarantees.(...) Nowadays, [adaptive methods] seems to denote any kind of coordinate-wise learning rates that does not guarantee anything in particular."
Orabona, F. (2019). A modern introduction to online learning.
adaptive methods
f(x_t) - f(x_*) \displaystyle \lesssim \left( 1 - O\Big(\frac{1}{\kappa}\Big) \right)^t
only guarantee (globally)
In Smooth
and Strongly Convex optimization,
Should be better if there is a good Preconditioner \(P\)
Can we get a line-search analog for diagonal preconditioners?
State of Affairs
"AdaGrad inspired an incredible number of clones, most of them with similar, worse, or no regret guarantees.(...) Nowadays, [adaptive methods] seems to denote any kind of coordinate-wise learning rates that does not guarantee anything in particular."
Orabona, F. (2019). A modern introduction to online learning.
Online Learning
Smooth Optimization
1 step-size
\(d\) step-sizes
(diagonal preconditioner )
Backtracking Line-search
Diagonal AdaGrad
Multidimensional Backtracking
Scalar AdaGrad
(and others)
(and others)
Preconditioner Search
Optimal (Diagonal) Preconditioner
\displaystyle \frac{1}{\kappa} P^{-1} \preceq \nabla^2 f(x) \preceq P^{-1}
Optimal step-size: biggest that guarantees progress
Optimal preconditioner: biggest (??) that guarantees progress
\displaystyle P = \tfrac{1}{L} I
\displaystyle \kappa = \tfrac{L}{\mu}
\(L\)-smooth
\(\mu\)-strongly convex
\(f\) is
and
\preceq \nabla^2 f(x) \preceq
L \cdot I
\mu \cdot I
Optimal Diagonal Preconditioner
\(\kappa_* \leq \kappa\), hopefully \(\kappa_* \ll \kappa\)
Over diagonal matrices
\displaystyle P_*
minimizes \(\kappa_*\) such that
\displaystyle \frac{1}{\kappa_*} P^{-1} \preceq \nabla^2 f(x) \preceq P^{-1}
From Line-search to Preconditioner Search
Line-search
\displaystyle \Bigg\{
Worth it if \(\sqrt{2d} \kappa_* \ll 2 \kappa\)
\displaystyle f(x_t) - f(x_*) \leq\Big(1 - \phantom{\frac{1}{2}} \cdot \frac{1}{\kappa}\Big)^t (f(x_0) - f(x_*))
\displaystyle
\frac{1}{2}
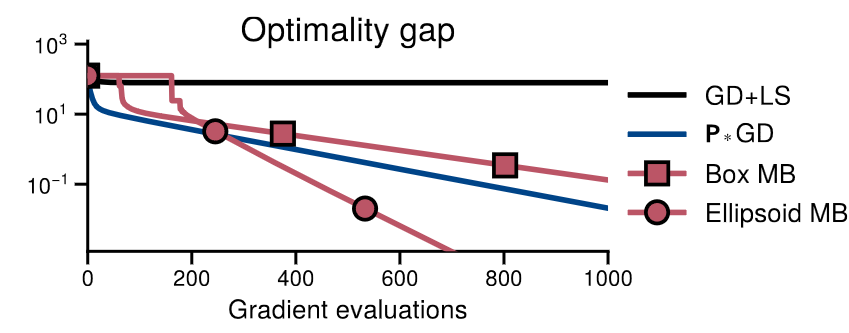
Multidimensional Backtracking
\displaystyle \Bigg\{
(our algorithm)
# backtracks \(\lesssim\)
\displaystyle d \cdot \log\Big( \alpha_0 \cdot L\Big)
\displaystyle f(x_t) - f(x_*) \leq\Big(1 - \phantom{\frac{1}{\sqrt{2d}}} \cdot \frac{1}{\phantom{\kappa_*}}\Big)^t (f(x_0) - f(x_*))
\displaystyle\frac{1}{\sqrt{2d}}
\displaystyle \kappa_*
# backtracks \(\leq\)
\displaystyle \log\Big(\alpha_{0} \cdot L \Big)
Multidimensional Backtracking
Why Naive Search does not Work
Line-search: test if step-size \(\alpha_{max}/2\) makes enough progress:
\displaystyle f(x_{t+1}) \leq f(x_t) - \tfrac{\alpha_{\max}}{2} \tfrac{1}{2} \lVert \nabla f(x_t) \rVert_2^2
Armijo condition
If this fails, cut out everything bigger than \(\alpha_{\max}/2\)
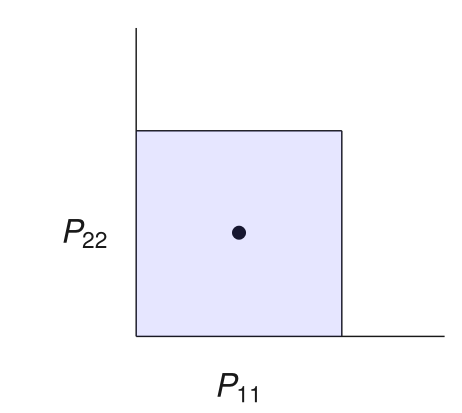
Preconditioner search:
0
\alpha_{0}
\tfrac{\alpha_{0}}{2}
\tfrac{1}{L}
\tfrac{\alpha_{0}}{4}
Test if preconditioner \(P\) makes enough progress:
Candidate preconditioners: diagonals in a box/ellipsoid
If this fails, cut out everything bigger than \(P\)
\displaystyle f(x_{t+1}) \leq f(x_t)
- \tfrac{1}{2} \lVert \nabla f(x_t) \rVert_P^2
Why Naive Search does not Work
Line-search:
\displaystyle f(x_{t+1}) \leq f(x_t) - \tfrac{\alpha_{\max}}{2} \tfrac{1}{2} \lVert \nabla f(x_t) \rVert_2^2
"Progress if \(f\) were
\(\frac{2}{\alpha_{\max}}\)-smooth"
If this fails, cut out everything bigger than \(\alpha_{\max}/2\)
0
\alpha_{\max}
\tfrac{\alpha_{\max}}{2}
\tfrac{1}{L}
\tfrac{\alpha_{\max}}{4}
Test if step-size \(\alpha_{\max}/2\) makes enough progress:
Candidate step-sizes: interval \([0, \alpha_{\max}]\)
Why Naive Search does not Work
Preconditioner search:
Test if preconditioner \(P\) makes enough progress:
Candidate preconditioners: diagonals in a box/ellipsoid
If this fails, cut out everything bigger than \(P\)
"Progress if \(f\) were
\(P\)-smooth"
\displaystyle f(x_{t+1}) \leq f(x_t)
- \tfrac{1}{2} \lVert \nabla f(x_t) \rVert_P^2
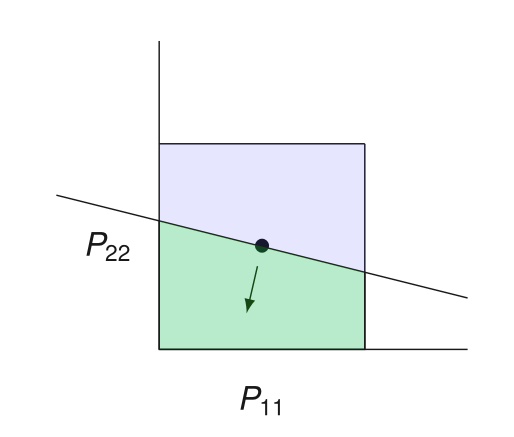
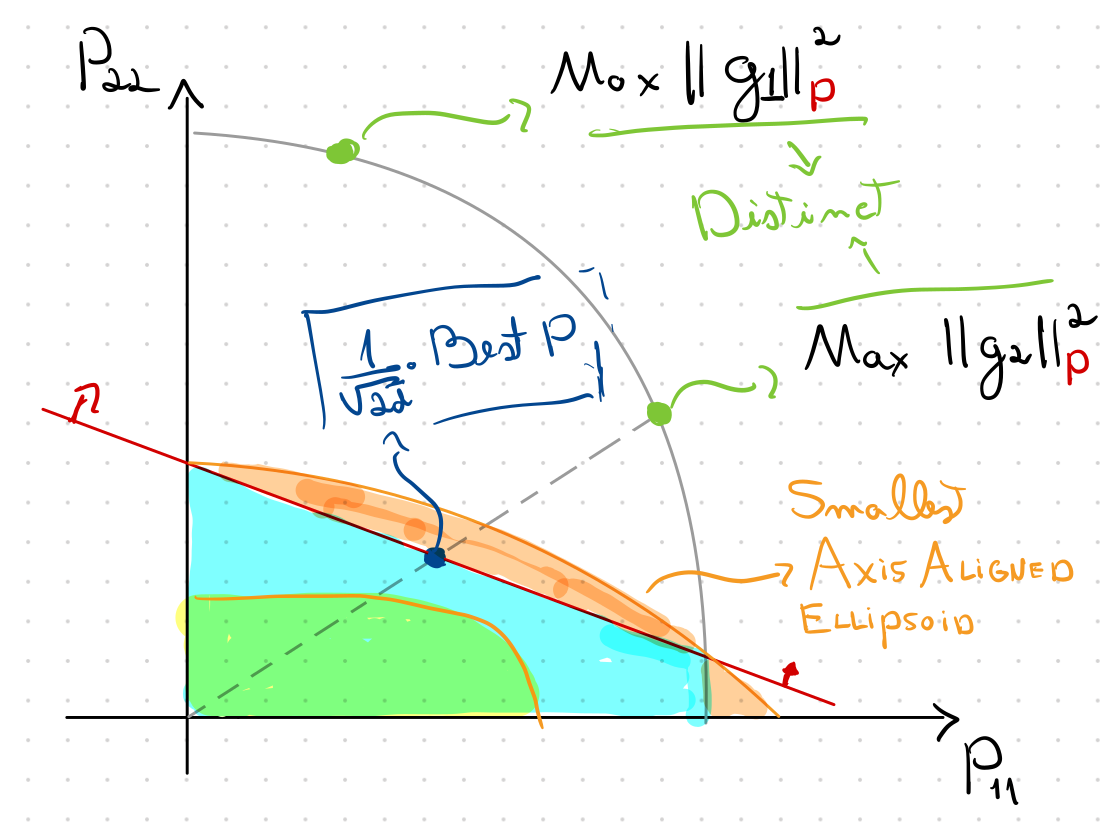
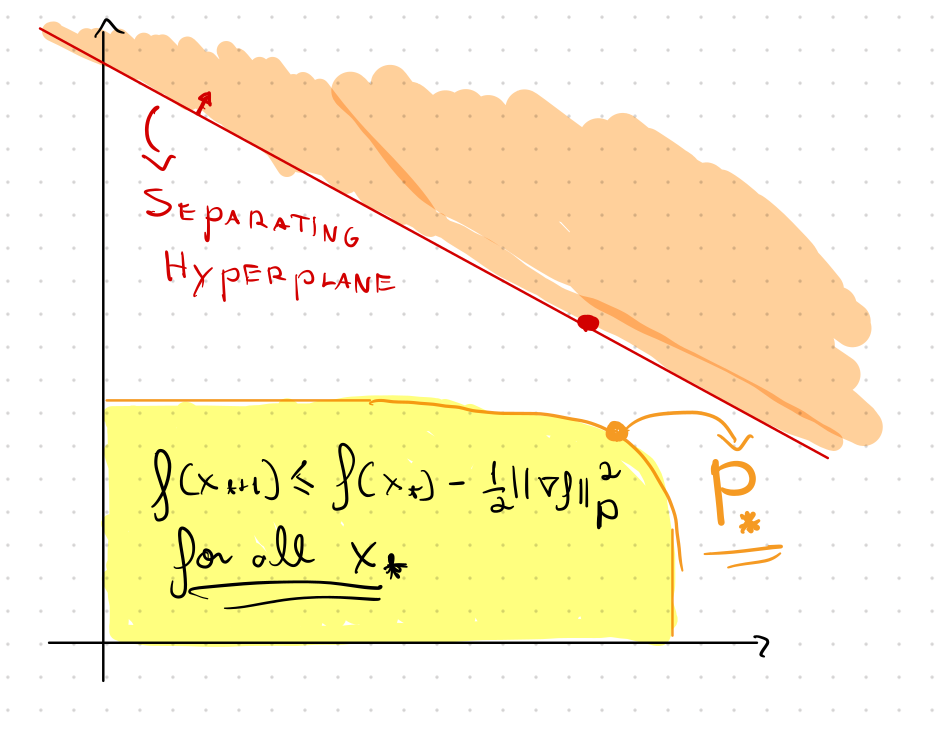
Convexity to the Rescue
\(P\) does not yield sufficient progress
Which preconditioners can be thrown out?
\(P \) yields sufficient progress \(\iff\) \(h(P) \leq 0\)
\displaystyle \nabla h(P)
Convexity \(\implies\)
induces a separating hyperplane!
"Hypergradient"
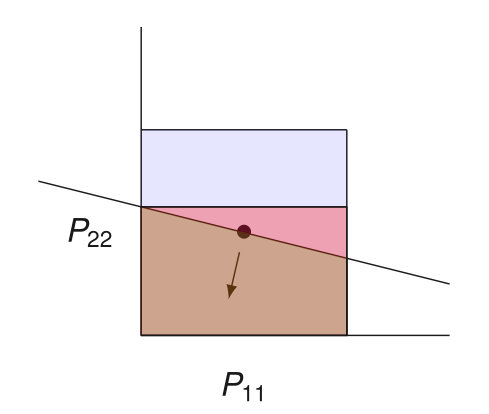
Main technical Idea
\displaystyle
h(P) = \phantom{f(x - P \nabla f(x)) - (f(x) - \tfrac{1}{2} \lVert \nabla f(x) \rVert_P^2)}
\displaystyle
\phantom{h(P) = f(x - P \nabla f(x)) }- (f(x) - \tfrac{1}{2} \lVert \nabla f(x) \rVert_P^2)
\displaystyle
\phantom{h(P) = }f(x - P \nabla f(x))\phantom{ - (f(x) - \tfrac{1}{2} \lVert \nabla f(x) \rVert_P^2)}
Boxes vs Ellipsoids
Box case: query point needs to be too close to the origin
\displaystyle f(x_t) - f(x_*) \lesssim\Big(1 - \phantom{\frac{1}{d}} \cdot \frac{1}{\kappa_*}\Big)^t
\displaystyle
\frac{1}{d}
Volume decrease \(\implies\) query points close to the origin
Good convergence rate \(\implies\) query point close to the boundary
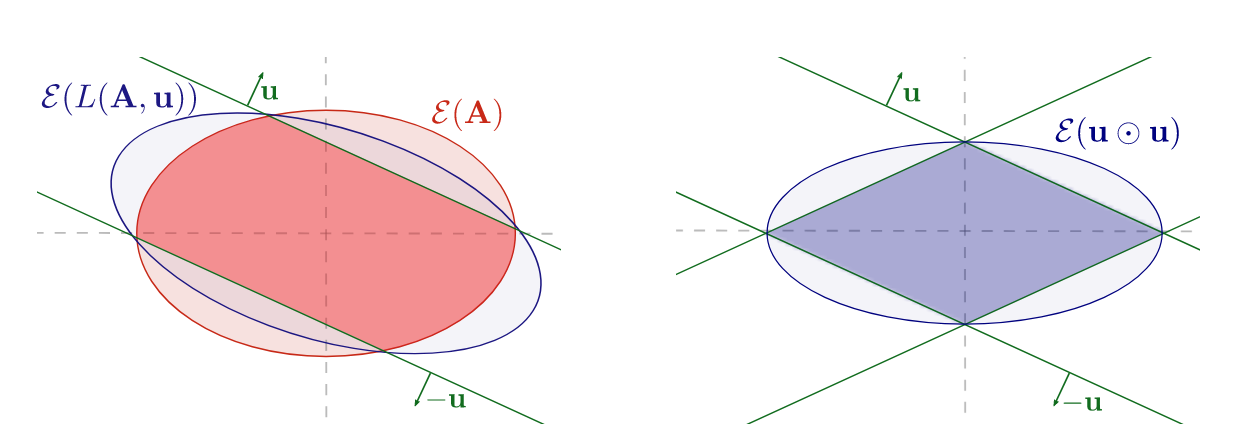
Ellipsoid method might be better.
\(\Omega(d^3)\) time per iteration
Ellipsoid Method with Symmetry
We want to use the Ellipsoid method as our cutting plane method
\(\Omega(d^3)\) time per iteration
We can exploit symmetry!
\(O(d)\) time per iteration
Constant volume decrease on each CUT
\displaystyle f(x_t) - f(x_*) \lesssim\Big(1 - \phantom{\frac{1}{\sqrt{2d}}} \cdot \frac{1}{\kappa_*}\Big)^t
\displaystyle
\frac{1}{\sqrt{2d}}
Query point \(1/\sqrt{2d}\) away from boundary
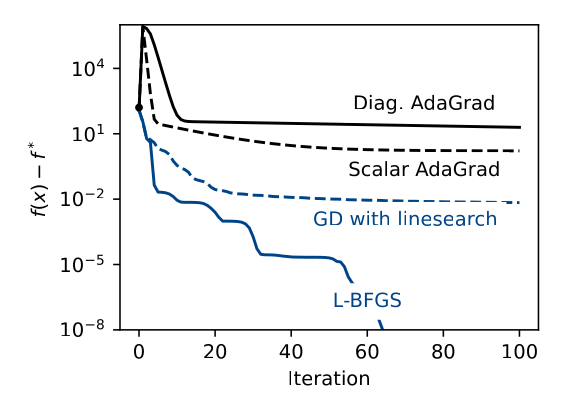
Experiments
\kappa \approx 10^{13}
\kappa_* \approx 10^{2}
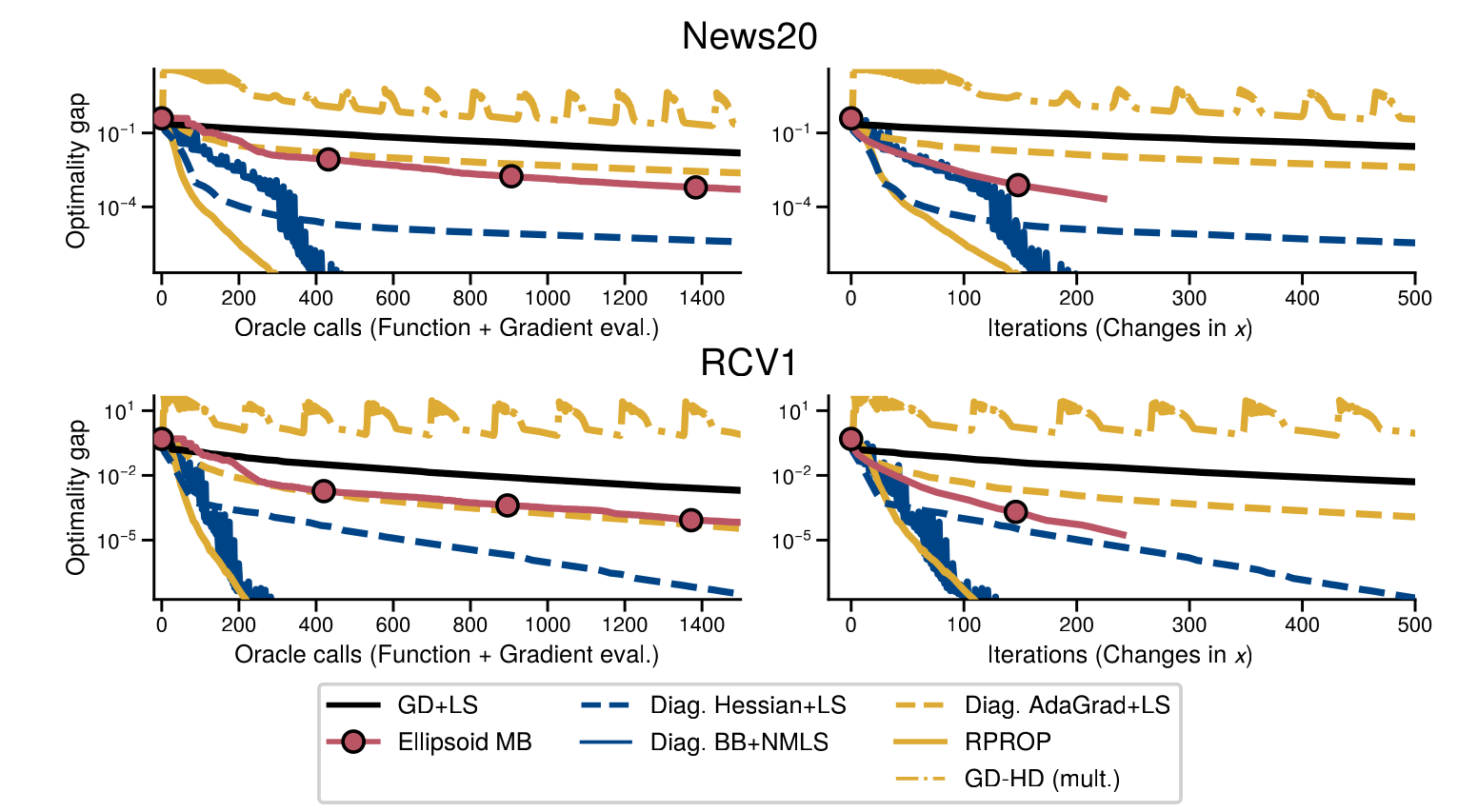
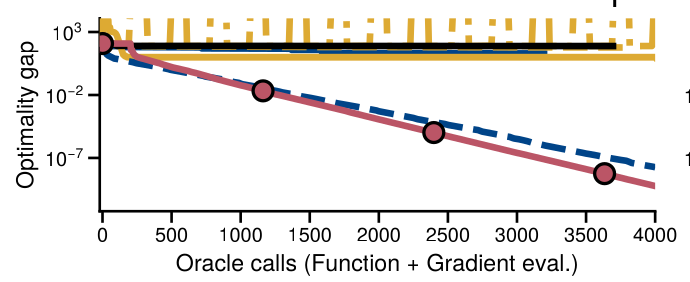
Experiments
Conclusions
Theoretically principled adaptive optimization method for smooth strongly convex optimization
A theoretically-informed use of "hypergradients"
ML Optimization meets Cutting Plane methods
Thanks!
arxiv.org/abs/2306.02527
Additional Slides
Box as Feasible Sets
How Deep to Query?
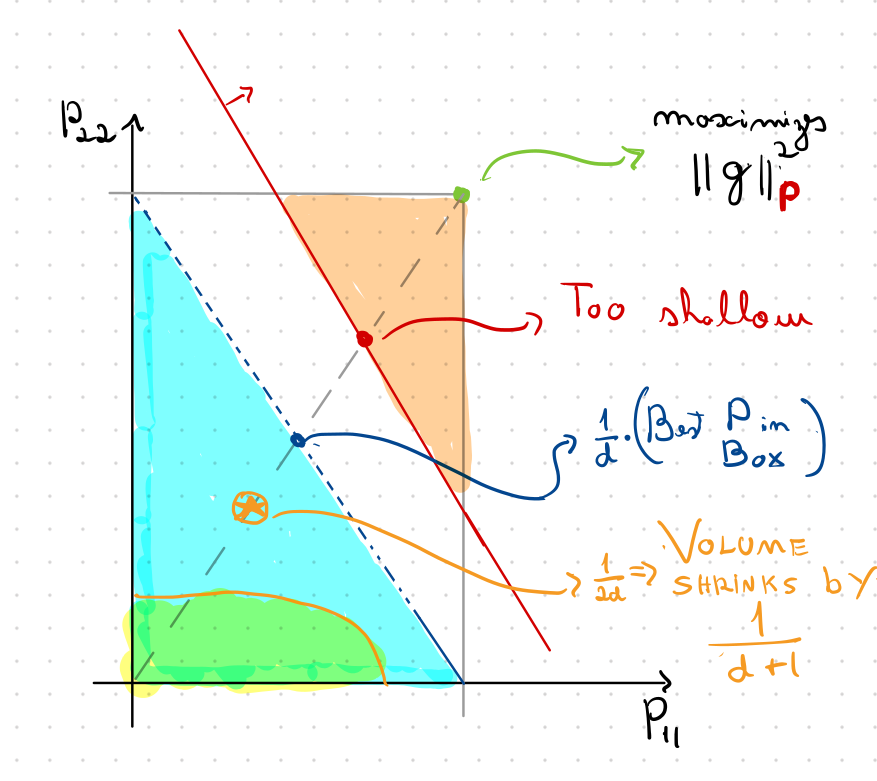
Ellipsoid Method to the Rescue
Convexity to the Rescue
Gradient Descent and Line Search
Why first-order optimization?
Training/Fitting a ML model is often cast a (uncontrained) optimization problem
Usually in ML, models tend to be BIG
\displaystyle \min_{x \in \mathbb{R}^{d}}~f(x)
\(d\) is BIG
Running time and space \(O(d)\) is usually the most we can afford
First-order (i.e., gradient based) methods fit the bill
(stochastic even more so)
Usually \(O(d)\) time and space per iteration
Convex Optimization Setting
\displaystyle f(y) \geq f(x) + \langle \nabla f(y), x - y\rangle + \frac{L}{2}\lVert x - y \rVert_2^2
\(f\) is convex
Not the case with Neural Networks
Still quite useful in theory and practice
\displaystyle \Bigg\{
More conditions on \(f\) for rates of convergence
\(L\)-smooth
\displaystyle \min_{x \in \mathbb{R}^{d}}~f(x)
\(\mu\)-strongly convex
\displaystyle f(y) \leq f(x) + \langle \nabla f(y), x - y\rangle + \frac{\mu}{2}\lVert x - y \rVert_2^2
Gradient Descent
\displaystyle x_{t+1} = x_t - \alpha \nabla f(x_t)
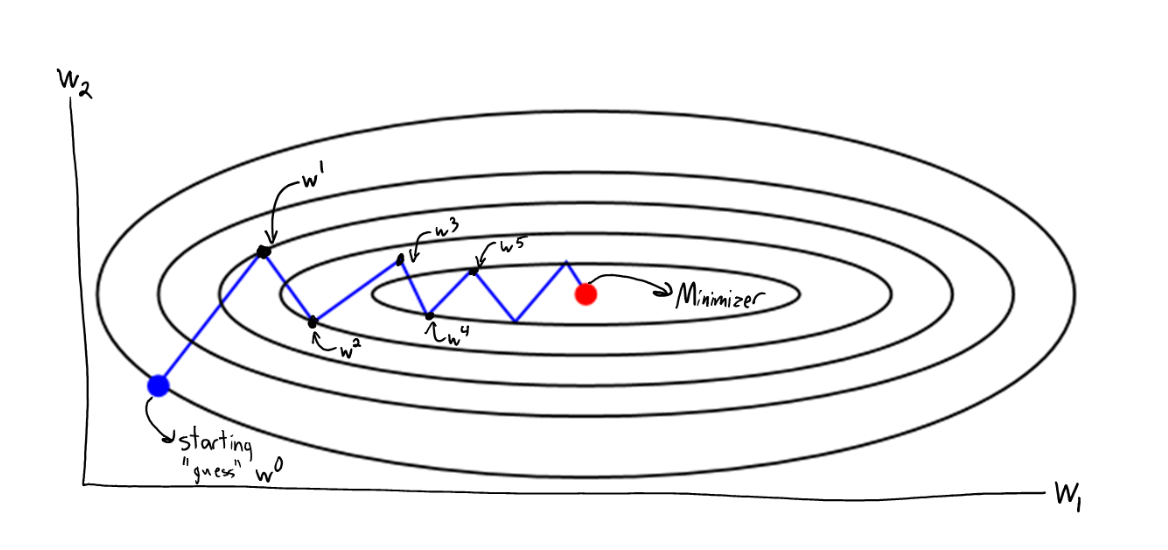
Which step-size \(\alpha\) should we pick?
\displaystyle \implies
\displaystyle f(x_t) - f(x_*) \leq \left( 1 - \frac{\mu}{L} \right)^t (f(x_0) - f(x_*))
Condition number
\displaystyle \alpha = \frac{1}{L}
\displaystyle \kappa = \frac{L}{\mu}
\(\kappa\) Big \(\implies\) hard function
What Step-Size to Pick?
If we know \(L\), picking \(1/L\) always works
and is worst-case optimal
What if we do not know \(L\)?
Locally flat \(\implies\) we can pick bigger step-sizes
\displaystyle x_{t+1} = x_t - \tfrac{1}{L} \nabla f(x_t)
If \(f\) is \(L\) smooth, we have
\displaystyle f(x_{t+1}) \leq f(x_t) - \tfrac{1}{L} \tfrac{1}{2} \lVert \nabla f(x_t) \rVert_2^2
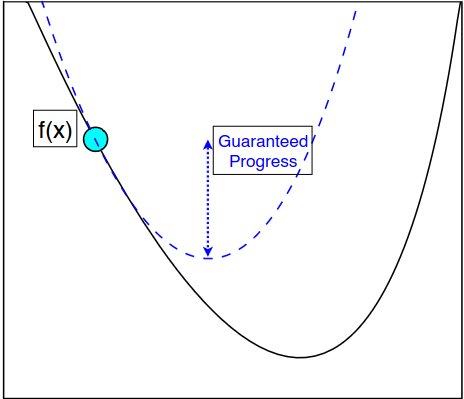
"Descent Lemma"
Idea: Pick \(\eta\) big and see if the "descent condition" holds
(Locally \(1/\eta\)-smooth)
Beyond Line-Search?
\displaystyle f(x) = x^T A x
\displaystyle A =
\begin{pmatrix}
1000 & 0 \\
0 & 0.001
\end{pmatrix}
\displaystyle \kappa = 10^{-6}
\displaystyle x_{t+1} = x_t -
\begin{pmatrix}
0.001 & 0 \\
0 & 1000
\end{pmatrix}
\nabla f(x_t)
Converges in 1 step
\(P\)
\(O(d)\) space and time \(\implies\) \(P\) diagonal (or sparse)
Can we find a good \(P\) automatically?
"Adapt to \(f\)"
Preconditioer \(P\)
"Adaptive" Optimization Methods
Adaptive and Parameter-Free Methods
\displaystyle x_{t+1} = x_t - P_t \cdot \nabla f(x_t)
Preconditioner at round \(t\)
AdaGrad from Online Learning
\displaystyle P_t = \Big( \sum_{i \leq t} \nabla f(x_i) \nabla f(x_i)^T \Big)^{1/2}
\displaystyle \mathrm{Diag}\Big( \sum_{i \leq t} \nabla f(x_i) \nabla f(x_i)^T \Big)^{1/2}
or
Better guarantees if functions are easy
while preserving optimal worst-case guarantees in Online Learning
Attains linear rate in classical convex opt (proved later)
But... Online Learning is too adversarial, AdaGrad is "conservative"
In OL, functions change every iteration adversarially
"Fixing" AdaGrad
But... Online Learning is too adversarial, AdaGrad is "conservative"
"Fixes": Adam, RMSProp, and other workarounds
"AdaGrad inspired an incredible number of clones, most of them with similar, worse, or no regret guarantees.(...) Nowadays, [adaptive] seems to denote any kind of coordinate-wise learning rates that does not guarantee anything in particular."
Francesco Orabona in "A Modern Introduction to Online Learning", Sec. 4.3
Hypergradient Methods
Idea: look at step-size/preconditioner choice as an optimization problem
Gradient descent on the hyperparameters
How to pick the step-size of this? Well...
Little/ No theory
Unpredictable
... and popular?!
Second-order Methods
P_t = \nabla^2 f(x_t)
Newton's method
is usually a great preconditioner
Superlinear convergence
...when \(\lVert x_t - x_*\rVert\) small
Newton may diverge otherwise
Using step-size with Newton and QN method ensures convergence away from \(x_*\)
Worse than GD
\displaystyle f(x_t) - f(x_*) \leq \left( 1 - \frac{1}{\kappa^2} \right)^t (f(x_0) - f(x_*))
\displaystyle \phantom{\kappa}^2
\(\nabla^2 f(x)\) is usually expensive to compute
P_t \approx \nabla^2 f(x_t)
should also help
Quasi-Newton Methods, e.g. BFGS
State of Affairs
(Quasi-)Newton: needs Hessian, can be slower than GD
Hypergradient methods: purely heuristic, unstable
Online Learning Algorithms: Good but pessimistic theory
at least for smooth optimization it seems pessimistic...
Online Learning
Smooth Optimization
1 step-size
\(d\) step-sizes
(diagonal preconditioner )
Backtracking Line-search
Diagonal AdaGrad
Coordinate-wise
Coin Betting
(non-smooth opt?)
Multidimensional Backtracking
Scalar AdaGrad
Coin-Betting
What does it mean for a method to be adaptive?
Preconditioner Search - NeurIPS 5 min
By Victor Sanches Portella
