Seminario AGCO
Victor Sanches Portella
October, 2025
ime.usp.br/~victorsp
for lower bounds in Differential Privacy
Fingerprinting Techniques
and a New Fingerprinting Lemma
Who am I?
Postdoc at USP - Brazil
ML Theory
Optimization
Randomized Algs
Optimization
p_t
1 - p_t
My interests according to a student:
"Crazy Algorithms"
Privacy? Why, What, and How
What do we mean by "privacy" in this case?
Informal Goal: Output should not reveal (too much) about any single individual
Different from security breaches (e.g., server invasion)
Output
Data Analysis
Trivial if output does not need to have information about the population
Real-life example - Netflix Dataset
Take Away from Examples
Privacy is quite delicate to get right
Hard to take into account side information
"Anonymization" is hard to define and implement properly
Different use cases require different levels of protection
Differential Privacy
Anything learned with an individual in the dataset
can (likely) be learned without
\displaystyle
\mathcal{M}
\displaystyle
\mathcal{M}
Indistinguishible
Differential Privacy (Formally)
\forall S
Any pair of neighboring datasets: they differ in one entry
\(\mathcal{M}\) is \((\varepsilon, \delta)\)-Differentially Private if
\mathbb{P}(\mathcal{M}(X) \in S)
\leq
e^{\varepsilon} \cdot \mathbb{P}(\mathcal{M}(X') \in S) + \delta
Definition:
\forall S
\((\varepsilon, \delta)\)-DP
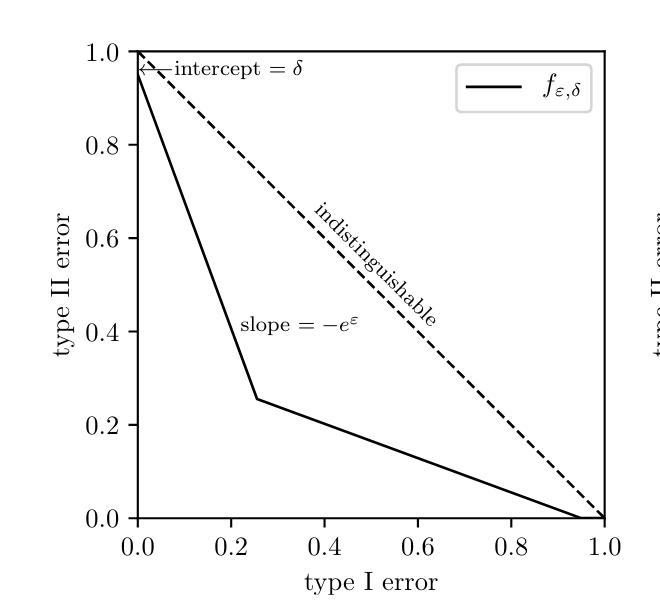
\(\varepsilon \equiv \) "Privacy leakage", constant (in theory \(\leq 1\))
\(\delta \equiv \) "Chance of catastrophic privacy leakage"
usually \(\ll 1/|X|\)
\displaystyle
\Bigg \{
Definition is a bit cryptic, but implies limit on power of hypothesis test of an adversary
\(\mathcal{M}\) needs to be randomized to satisfy DP
Interpretation of DP: Hard to Hypothesis Test
\(H_0:\) Output is from \(\mathcal{M}(X)\)
\(H_1:\) Output is from \(\mathcal{M}(X')\)
Some Advantages of Differential Privacy
Worst case: No assumptions on the adversary
Composable: DP guarantees compose nicely
Loose!
\mathcal{M}_1
\mathcal{M}_2
\((\varepsilon_1, \delta_1)\)-DP
\((\varepsilon_2, \delta_2)\)-DP
\(\implies\)
Both together are
\((\varepsilon_1 +\varepsilon_2, \delta_1 + \delta_2)\)-DP
DP and Other Areas of ML and TCS
Online Learning
Adaptive Data Analysis and Generalization in ML
Robust statistics
An Example: Computing the Mean
Goal:
is small
\mathcal{M}
\((\varepsilon, \delta)\)-DP such that approximates the mean:
Algorithm:
\displaystyle
\mathcal{M}(x) = \mathrm{Mean}(x) + Z
Gaussian or Laplace noise
X = (x_1, \dotsc, x_n)
x_i \in [-1,1]^d
with
\mathbb{E}\Big[\lVert \mathcal{M}(X) - \mathrm{Mean}(x)\rVert \Big]
Example 2: Computing the Mean of Gaussian
Goal:
is small
\mathcal{M}
\((\varepsilon, \delta)\)-DP such that approximates the mean \(\mu\):
X = (x_1, \dotsc, x_n)
x_i \sim \mathcal{N}(\mu, 1)
with
\mathbb{E}\Big[\lVert \mathcal{M}(X) - \mu\rVert \Big]
DP guarantee is still worst-case
Accuracy is good only for Gaussian input
Lower Bounds: How many samples \(n\) do we need to get \(\alpha\) error with privacy?
Fingerprinting Codes
A Lower Bound Strategy
Assume \(\mathcal{M}\) is
accurate
Adversary can detect some \(x_i\)
with high probability
Feed to \(\mathcal{M}\) a marked input \(X\)
\((\varepsilon,\delta)\)-DP implies adversary detects \(x_i\) on \(\mathcal{M}(X')\) with
\(X' = X - \{x_i\} + \{z\}\)
CONTRADICTION
(false positive)
Avoiding Pirated Movies via Fingerprinting
Movie may leak!
Movie Owner
Can we detect one ?
?
Idea: Mark some of the scenes (Fingerprinting)
Fingerprinting Codes
\(d\) scenes
\(n\) copies of the movie
1 = marked scene
0 = unmarked scene
Code usually randomized
We can do with \(d = 2^n\). Can \(d\) be smaller?
Example of pirating:
\begin{pmatrix}
1 \\
0 \\
1
\end{pmatrix}
\begin{pmatrix}
1 \\
1 \\
0
\end{pmatrix}
\begin{pmatrix}
1 \\
0 \\
0
\end{pmatrix}
\(0\) or \(1\)
\(0\) or \(1\)
Only 1
\displaystyle \Bigg (
\displaystyle \Bigg )
Goal of fingerprinting
Given a copy, trace back one with prob. false positive \(\ll 1/n\)
\begin{pmatrix}
1\\
0 \\
0 \\
\vdots\\
1 \\
\end{pmatrix}
\begin{pmatrix}
1\\
1 \\
0 \\
\vdots\\
1 \\
\end{pmatrix}
\begin{pmatrix}
1\\
1 \\
0 \\
\vdots\\
1 \\
\end{pmatrix}
\begin{pmatrix}
0\\
0 \\
1 \\
\vdots\\
0 \\
\end{pmatrix}
\cdots
\begin{pmatrix}
1\\
0 \\
1 \\
\vdots\\
1 \\
\end{pmatrix}
Fingerprinting Codes for Lower Bounds
Assume \(\mathcal{M}\) is
accurate
Adversary can detect some \(x_i\)
with high probability
Feed to \(\mathcal{M}\) a marked input \(X\)
\((\varepsilon,\delta)\)-DP implies adversary detects \(x_i\) on \(\mathcal{M}(X')\) with
\(X' = X - \{x_i\} + \{z\}\)
CONTRADICTION
FP codes with \(d = \tilde{O}(n^2)\)
Output -> Pirated Movie
Breaks False Positive Guarantee
[Tardos '08]
The Good, The Bad, and The Ugly of Codes
The Ugly:
Black-box use of FP codes \(\implies\) hard to adapt to specific use cases
The Bad:
Very restricted to binary inputs
The Good:
Leads to optimal lower bounds for a variety of problems
Fingerprinting Lemmas
Fingerprinting Lemma - Mean Estimation
\displaystyle
\mathbb{E}[(\mathcal{M}(X) - \mu) \cdot (x_i - \mu)]
If \(\mathcal{M}\) is accurate (approximates \(\mu\))
is large (on average)
\displaystyle
\mu
\displaystyle
x_3
\displaystyle
x_2
\displaystyle
x_4
\displaystyle
\mathcal{M}(X)
\displaystyle
x_1
Not true for all \(\mathcal{M}\) if \(x_i\) and \(\mu\) are not randomized
Idea: For some distribution on the input,
the output is highly correlated with the input
(\(\mathcal{M}\) can "memorize" the input \(X\) or the anwer \(\mu\))
"Correlation" of output \(\mathcal{M}(X)\) and input \(x_i\)
\mathbb{E}[x_i] = \mu
Fingerprinting Lemma - Picture
\displaystyle
\mathbb{E}[\mathcal{A}(x_i, \mathcal{M}(X))]
If \(\mathcal{M}\) is accurate
large
\displaystyle
\mathbb{E}[|\mathcal{A}(z, \mathcal{M}(X))|]
If \(z\) indep. of \(X\)
small
\mathcal{A}(z, \mathcal{M}(X)) = (\mathcal{M}(X) - \mu) \cdot (z - \mu)
\displaystyle
\mu
\displaystyle
\mathcal{M}(X)
\displaystyle
z
\displaystyle
z
\displaystyle
z
\displaystyle
z
\displaystyle
\mu
\displaystyle
x_3
\displaystyle
x_2
\displaystyle
x_4
\displaystyle
\mathcal{M}(X)
\displaystyle
x_1
Depends on distribution of \(X\) and \(\mu\)
Fingerprinting Lemmas
Idea: For some distribution on the input,
the output is highly correlated with the input
Lemma (A 1D Fingerprinting Lemma, [Bun, Stein, Ullman '16])
\(\mu \sim \mathrm{Unif}(\{-1,1\})\)
\(x_1, \dotsc, x_n \in \{\pm 1\}\) with \(\mathbb{E}[x_i] = \mu\)
\displaystyle \mathbb{E}\Big [\sum_{i = 1}^n (\mathcal{M}(X) - \mu) \cdot (x_i - \mu) \Big ] \geq \frac{1}{10}
"Correlation" between \(x_i\) and \(\mathcal{M}(X)\)
\(\mathcal{A}(x_i, \mathcal{M}(X))\)
If \(\mathcal{M}\) estimates \(\mu\) well,
From 1D Lemma to a Code(-Like) Object
Fingerprinting Lemma leads to a kind of fingerprinting code
Bonus: quite transparent and easy to describe
Key Idea: Make \(d = \tilde{O}(n^2)\) independent copies
\(\mu \sim \mathrm{Unif}(\{-1,1\})^d\) a random vector
\(x_1, \dotsc, x_n \in \{\pm 1\}^d\) such that \(\mathbb{E}[x_i] = \mu\)
\displaystyle \mathbb{P}\Big [\sum_{i = 1}^n \mathcal{A}(x_i, \mathcal{M}(X)) \leq d/20 \Big ] \leq \frac{1}{n^3}
for \(d = \Omega(n^2 \log n)\)
Insight: we do not need to go back to codes to get lower bounds
From Lemma to Lower Bounds
\displaystyle \mathbb{E}\Big [\sum_{i = 1}^n \mathcal{A}(x_i, \mathcal{M}(X)) \rangle \Big ] \gtrsim d
\displaystyle \mathbb{E}\Big [\sum_{i = 1}^n \mathcal{A}(x_i, \mathcal{M}(X)) \Big ] \lesssim
n \varepsilon \cdot
\sqrt{\mathbb{E}[{\lVert\mathcal{M}(X) - p\rVert_2^2}]}
\displaystyle \mathbb{E}[ \mathcal{A}(x_i, \mathcal{M}(X))] \approx \mathbb{E}[\mathcal{A}(x_i, \mathcal{M}(X_{-i}))]
\displaystyle \implies\frac{d}{n} \lesssim \sqrt{\mathbb{E}[{\lVert\mathcal{M}(X) - p\rVert_2^2}]}
If \(\mathcal{M}\) is accurate, correlation is high
If \(\mathcal{M}\) is \((\varepsilon, \delta)\)-DP, correlation is low
Independence of coordinates of \(\mu\) helps a lot here
Lower Bound to Distribution Estimation
Different from codes, structure of input is clear in FP Lemmas
\(\mu \sim \mathrm{Unif}(\{-1,1\})^d\) a random vector
\(x_1, \dotsc, x_n \in \{\pm 1\}^d\) such that \(\mathbb{E}[x_i] = \mu\)
Implies lower bounds for Radamacher inputs (easier than worst-case)
We can adapt to other settings!
Example:
\(\mu \sim \mathcal{N}(0, I_{d \times d})\) a random vector
\(x_1, \dotsc, x_n \in \mathcal{N}(\mu, I_{d \times d})\)
Lower Bounds for Gaussian
Covariance Matrix Estimation
Work done in collaboration with Nick Harvey
Privately Estimating a Covariance Matrix
\displaystyle
x_1, x_2, \dotsc, x_n \sim \mathcal{N}(0, \Sigma)
\displaystyle
\Sigma \succ 0
Unknown Covariance Matrix
\displaystyle
X \in \mathbb{R}^{d \times n}
\((\varepsilon, \delta)\)-differentially private \(\mathcal{M}\) to estimate \(\Sigma\)
on \(\mathbb{R}^d\)
Goal:
Required even without privacy
Required even for \(d = 1\)
Is this tight?
Exists \((\varepsilon, \delta)\)-DP \(\mathcal{M}\) such that
\displaystyle
n = \tilde O\Big(\frac{d^2}{\alpha^2} + \frac{\log(1/\delta)}{\varepsilon} + \frac{d^2}{\alpha \varepsilon}\Big)
\displaystyle
\mathbb{E}[\lVert\mathcal{M}(X) - \Sigma\rVert_F^2] \leq \alpha^2
samples
Known algorithmic results
with
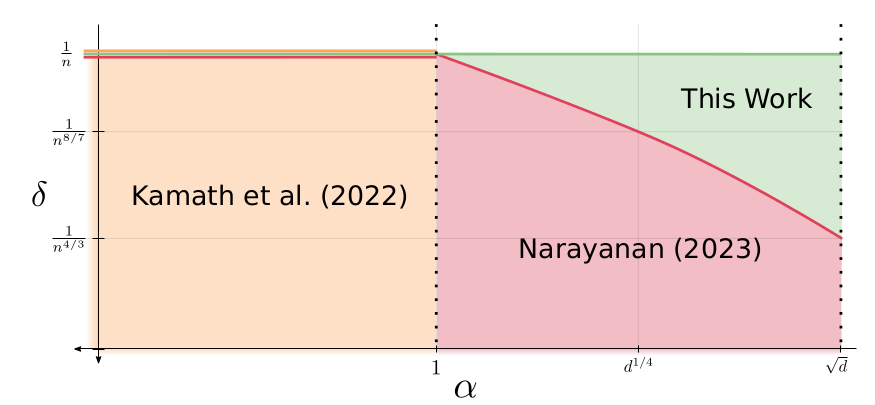
Our Results - New Lower Bounds
Theorem
For any \((\varepsilon, \delta)\)-DP algorithm \(\mathcal{M}\) such that
\displaystyle
\mathbb{E}\big[\lVert\mathcal{M}(X) - \Sigma\rVert_F^2\big] \leq \alpha^2 = O(d)
and
\displaystyle
\delta = O\Big( \frac{1}{n \ln n}\Big)
we have
\displaystyle
n = \Omega\Big(\frac{d^2}{\alpha\varepsilon}\Big)
Above 1/n, DP may not be meaningful
Previous
\displaystyle
n = \Omega\big(\tfrac{d^2}{\alpha\varepsilon}\big)
Lower Bounds
\displaystyle
\tilde{O}(\tfrac{1}{n})
\displaystyle
\delta
\displaystyle
O(1)
\displaystyle
O(d)
Accuracy \(\alpha^2\)
New Fingerprinting Lemma using
Stokes' Theorem
Follow up:
LBs for other problems
[Lyu & Talwar ´25]
Roadblocks to Fingerprinting Lemmas
\displaystyle
x_1, x_2, \dotsc, x_n \sim \mathcal{N}(0, \Sigma)
\displaystyle
\Sigma \succ 0
Unknown Covariance Matrix
on \(\mathbb{R}^d\)
To get a Fingerprinting Lemma, we need random \(\Sigma\)
How can we make \(\Sigma\) random, \(\succeq 0\), and with independent entries?
[Kamath, Mouzakis, Singhal '22]
Diagonally dominant matrices!
Problem: 0 matrix has error \(O(1)\)
\mathbb{E}[\lVert \mathcal{M}(X) - 0 \rVert_F^2 ] = O(1)
Can't lower bound accuracy of algorithms with \(\omega(1)\) error
Diagonal
= \frac{3}{4} \pm \frac{1}{4d}
Off-diagonal
= \pm \frac{1}{2d}
How to avoid independent entries?
Which Distribution to Use?
Wishart Distribution
Our results use a very natural distribution:
\displaystyle
\Sigma = \frac{1}{2d} \; G \; G^{T}
\(d \times 2d\) random Gaussian matrix
\displaystyle
\succeq 0
Natural distribution over PSD matrices
Entries are highly correlated
A Different Correlation Statistic
\displaystyle
\mathcal{A}(z, \mathcal{M}(X)) = \big\langle\mathcal{M}(X) - \Sigma, \mathrm{Score}(z \;|\; \Sigma))\big\rangle
Gaussian Score function
Score Attack Statistic
"Usual" choice
\displaystyle
\mathcal{A}(z, \mathcal{M}(X)) = \langle\mathcal{M}(X) - \Sigma, z z^{\intercal} - \Sigma \rangle
\displaystyle
zz^{\intercal}
\displaystyle
\mathcal{M}(X)
\displaystyle
\Sigma
[Cai et al. 2023]
\displaystyle
I
\displaystyle
\mathcal{M}(X)
\displaystyle
zz^{\intercal}
\displaystyle
\Sigma^{-1/2}
\displaystyle
\Sigma^{-1/2}
\displaystyle
\Sigma^{-1/2}
\displaystyle
\Sigma^{-1/2}
Original paper does not handle dependent entries!
But Why this \(\mathcal{A}\)?
Key Property in 1 Dimension for Estimating Mean
\displaystyle \mathbb{E}\Big [\sum_{i = 1}^n \mathcal{A}(M(X), x_i) \Big ] = g'(\mu)
\displaystyle g(\mu) = \mathbb{E}_{X}[\mathcal{M}(X) | \mu]
If \(g(\mu) = \mu\), done!
If \(\mathcal{M}(X)\) is accurate, we should have \(g(\mu) \approx \mu\)
Key Property in d Dimensions
\displaystyle \mathbb{E}\Big [\sum_{i = 1}^n \mathcal{A}(M(X), x_i) \Big ] =
\displaystyle
\sum_{i,j }\frac{\partial}{\partial\Sigma_{ij}} \; g(\Sigma)_{ij}
\displaystyle g(\Sigma) = \mathbb{E}_{X}[\mathcal{M}(X) | \Sigma]
Divergence of \(g\)
Final Ingredient: Stein's identity
Key Step in 1D:
Stein's Identity
\displaystyle \mathbb{E}[g'(\mu)] = \mathbb{E}[g(\mu) \mu]
for \(\mu \sim \mathcal{N}(0, 1/2)\)
Something similar holds for \(\mu\) uniform
Follows from Integration by Parts
\displaystyle \mathbb{E}\Big[
\sum_{i,j }\partial_{ij} \; g(\Sigma)_{ij}\Big]
Going to High Dimensions
Integration by Parts in High Dimensions
Stokes' Theorem
\(\Sigma \sim\) Wishart leads to elegant analysis
Stein-Haff Identity
Takeaways
Differential Privacy is a mathematically formal definition of private algorithms
Interesting connections to other areas of theory
Fingerprinting Codes lead to many optimal lower bounds for DP
Fingerprinting Lemmas are more versatile for lower bounds and can be adapted to other settings
New Fingerprinting Lemma escaping the need to bootstrap a 1D result to higher dimensions with independent copies
Thanks!
Seminario AGCO
for Lower Bounds
Differential Privacy
An Introduction to
Fingerprinting Techniques
and
Victor Sanches Portella
October, 2025
ime.usp.br/~victorsp
Real-life example - NY Taxi Dataset
Summary: License plates were anonymized using MD5
Easy to de-anonymize due to lincense plate structure
By Vijay Pandurangan
https://www.vijayp.ca/articles/blog/2014-06-21_on-taxis-and-rainbows--f6bc289679a1.html
An Example: Computing the Mean
\mathbb{E}\Big[\lVert \mathcal{M}(X) - \mathrm{Mean}(x)\rVert \Big]
Goal:
is small
\mathcal{M}
\((\varepsilon, \delta)\)-DP such that approximates the mean:
Algorithm:
\displaystyle
\mathcal{M}(x) = \mathrm{Mean}(x) + Z
Gaussian or Laplace noise
X = (x_1, \dotsc, x_n)
x_i \in [-1,1]^d
with
OPTIMAL?
Theorem
\(Z \sim \mathcal{N}(0, \sigma^2 I)\) with
\sigma \approx \frac{d}{n} \frac{\sqrt{\ln(1/\delta)}}{\varepsilon}
\(\mathcal{M}\) is \((\varepsilon, \delta)\)-DP and
\mathbb{E}\Big[\lVert \mathcal{M}(X) - \mathrm{Mean}(x)\rVert_2\Big]
\leq \sigma \approx \frac{d}{n} \frac{\sqrt{\ln(1/\delta)}}{\varepsilon}
Talk Fingerprinting - Chile
By Victor Sanches Portella
