35o Colóquio Brasileiro de Matemárica
for the Distinct Elements Problem
Privacy Guarantees
Intrinsic
Stable Random Projections
of
Victor Sanches Portella
July, 2025
ime.usp.br/~victorsp
Joint work with Nick Harvey and Zehui (Emily) Gong
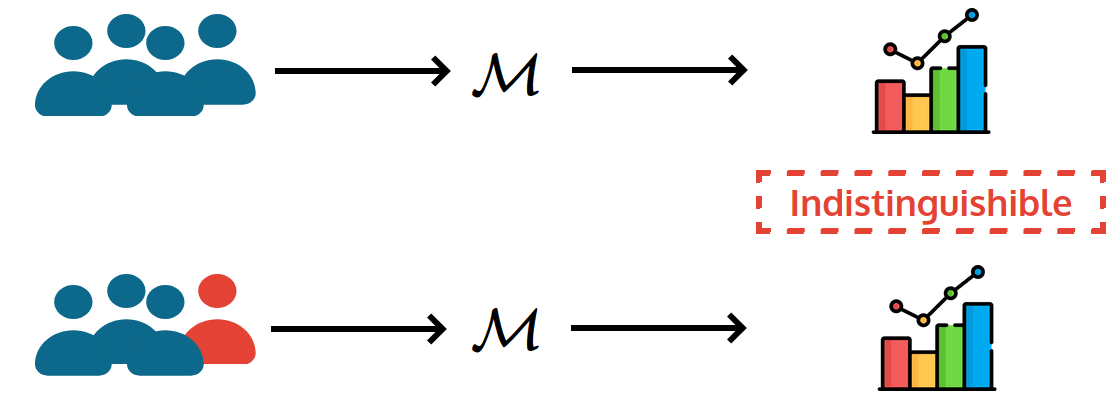
Privacy? Why, What, and How
What do we mean by "privacy" in this case?
Informal Goal: Output should not reveal (too much) about any single individual
Different from security breaches (e.g., server invasion)
Output
Data Analysis
Trivial if output does not need to have information about the population
Real-life example - Netflix Dataset
Differential Privacy
Anything learned with an individual in the dataset
can (likely) be learned without
\displaystyle
\mathcal{M}
\displaystyle
\mathcal{M}
Indistinguishible
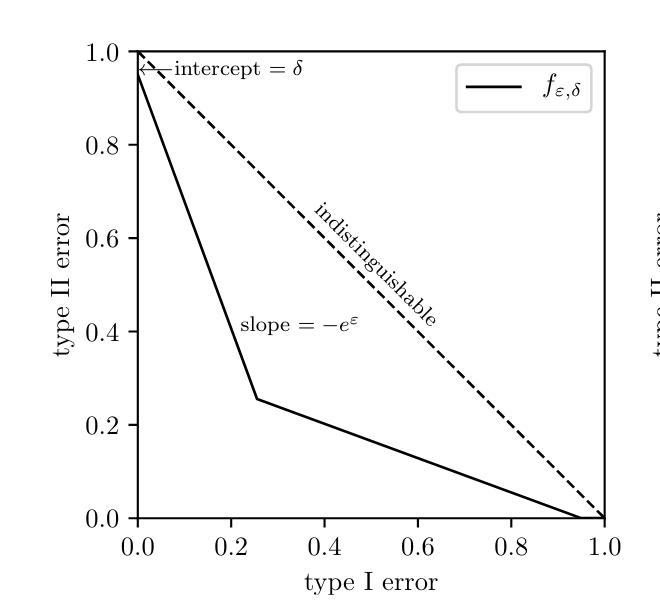
Differential Privacy (Formally)
Any pair of neighboring datasets: they differ in one entry
\(\mathcal{M}\) is \((\varepsilon, \delta)\)-Differentially Private if
\mathbb{P}(\mathcal{M}(X) \in S)
\leq
e^{\varepsilon} \cdot \mathbb{P}(\mathcal{M}(X') \in S) + \delta
Definition:
\forall S
\((\varepsilon, \delta)\)-DP
\(\varepsilon \equiv \) "Privacy leakage", constant (in theory \(\leq 1\))
\(\delta \equiv \) "Chance of catastrophic privacy leakage"
usually \(\ll 1/|X|\)
\displaystyle
\Bigg \{
Definition is a bit cryptic, but implies limit on power of hypothesis test of an adversary
\(\mathcal{M}\) needs to be randomized to satisfy DP
Interpretation of DP: Hard to Hypothesis Test
\(H_0:\) Output is from \(\mathcal{M}(X)\)
\(H_1:\) Output is from \(\mathcal{M}(X')\)
Some Advantages of Differential Privacy
Worst case: No assumptions on the adversary
Composable: DP guarantees compose nicely
Loose!
\mathcal{M}_1
\mathcal{M}_2
\((\varepsilon_1, \delta_1)\)-DP
\((\varepsilon_2, \delta_2)\)-DP
\(\implies\)
Both together are
\((\varepsilon_1 +\varepsilon_2, \delta_1 + \delta_2)\)-DP
A Few Topics I am Interested in DP
Learning Theory
Deep Ideas in Lower Bounds via Fingerprinting
Proof uses Ramsey's Theory
We are starting work on this
In this Talk: Revisiting Randomized Algorithms
Ongoing extension to optimization problems
Counting Distinct Elements
Counting Distinct Elements in a Stream
The problem:
Count (approx.) the number of distinct elements in a stream of \(N\) items of \(n\) types
Want to use \(o(n)\) space
Example: Counter of # of listeners of a song
Items arrive sequentially
\(N\) and \(n\) are LARGE
[Pokemon Icons by Roundicon Freebies at flaticon.com]
Distinct Elements via Sketching
Frequency vector \(f(x)\) of size \(n\)
Stream \(x\) of length \(N\)
3
2
1
1
Instead, use Small sketch
Allow us to track
# distinct elements of \(x\)
in small space
Stable Random Projections
Warm-up: Estimating the \(F_2\) norm
Goal:
Estimate \(\lVert f(x)\rVert_2^2 = f(x)_1^2 + f(x)_2^2 + \dotsm + f(x)_n^2\) of a stream \(x\)
3
2
1
1
2
2
2
2
+
+
+
\(\mathbb{E}\big [(Z^{\mathsf{T}} f(x))^2\big]= \lVert f(x)\rVert_2^2\)
but \(Z^{\mathsf{T}} f(x)\) maybe far from its expectation
Solution: Repeat \(r\) times and take the average
Key observation:
If \(Z \sim \mathcal{N}(0,I)\), then \(Z^{\mathsf{T}} f(x) \sim \mathcal{N}(0, \lVert f(x)\rVert_2^2\))
Warm-up: Estimating the \(F_2\) norm
\(r \times n\) Gaussian matrix
\(f(x)\)
\(=\)
\(\mathsf{sk}(x)\)
Sketch of size \(r\) to approximate \(\lVert f(x)\rVert_2^2\)
Matrix is too large
For each new item, we only need one column of the matrix
We can generate this matrix implicitly with low space using
pseudorandom generators
(Closely related to Johnson–Lindenstrauss)
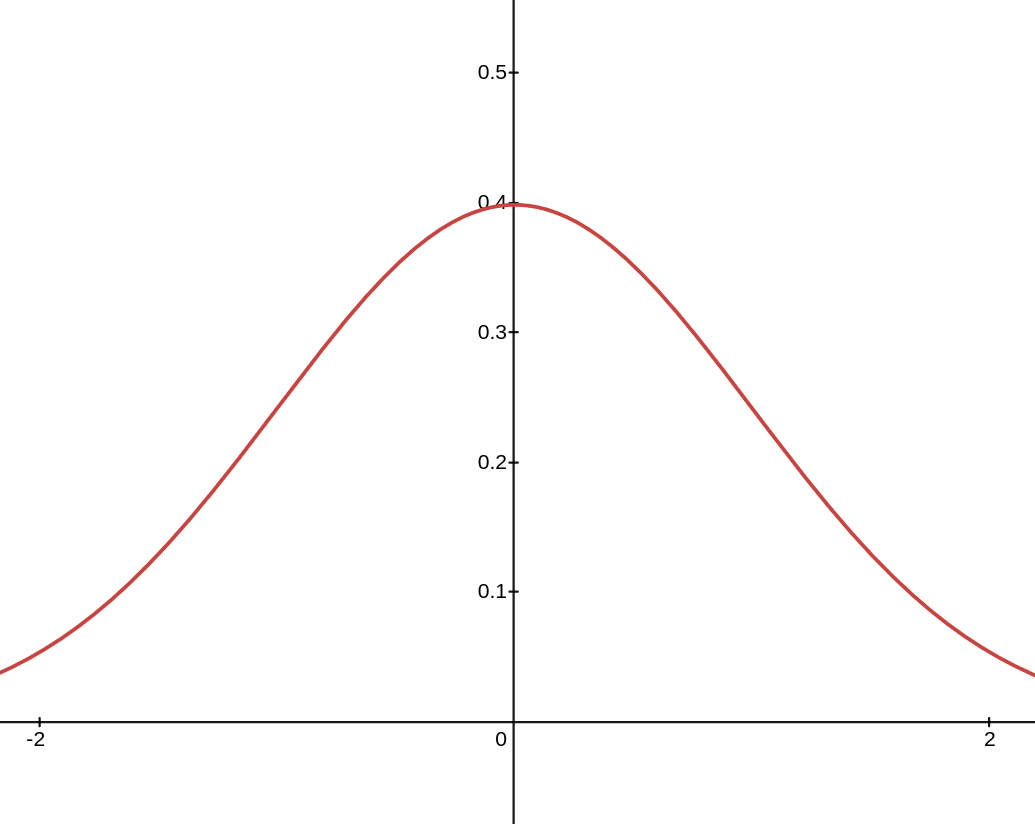
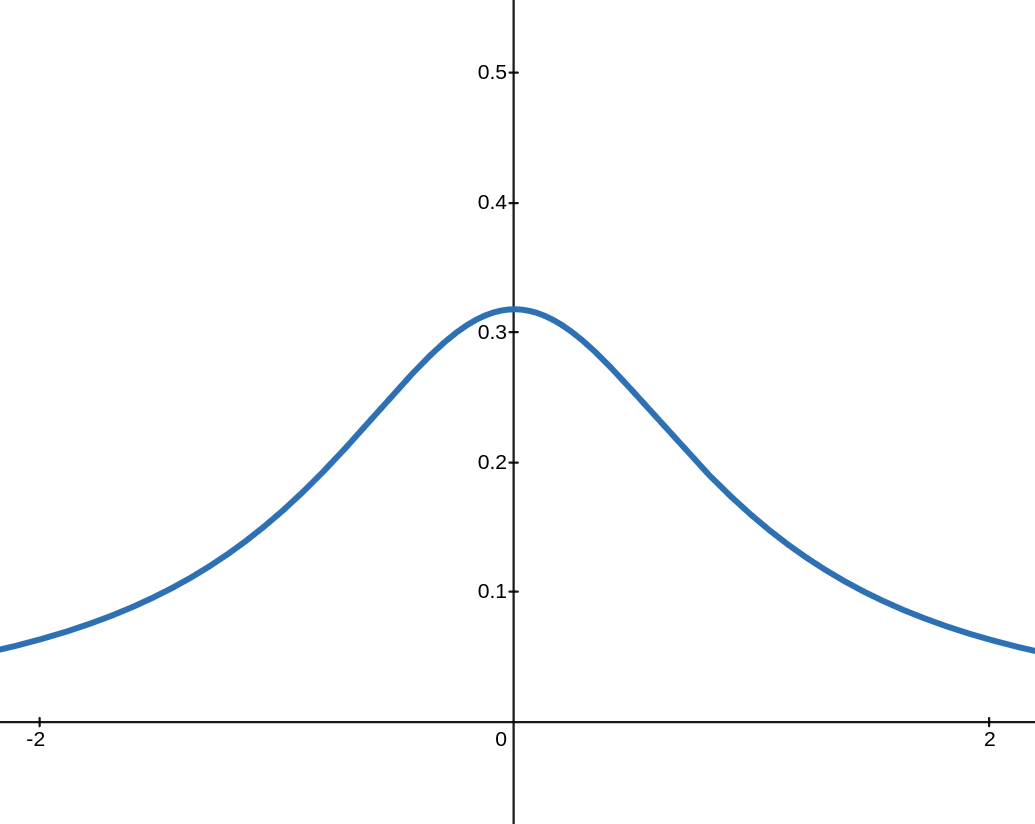
Stable Distributions
Stability of Gaussians:
a Z + b Y \sim (a^2 + b^2)^{1/2} \cdot \mathcal{N}(0,1)
If \(Z,Y \sim \mathcal{N}(0,1)\) are independent
a Z + b Y \sim (a^{\phantom{p}} + b^{\phantom{p}})^{1/\phantom{p}} \cdot \mathcal{D}_p
\(p\)-Stable Distribution \(\mathcal{D}_p\):
If \(Z,Y \sim \mathcal{D}_p\) are independent,
{}^{p}
{}^{p}
{}^{p}
Gaussian (\(p = 2\))
Cauchy (\(p = 1\))
Stable Projections
\(r \times n\)
\(p\)-Stable Matrix
\(f(x)\)
\(=\)
\(\mathsf{sk}(x)\)
Skecth of size \(r\) to approximate \(\lVert f(x)\rVert_p^p\)
For \(p\) small (\(p \leq 1/\lg n\)), \(\lVert f(x)\rVert_p^p \approx\) # distinct elements
Supports removals in the stream
Different sketches can be combined
3
2
1
1
\(p\)
\(p\)
\(p\)
\(p\)
+
+
+
Intrinsic Privacy of
Random Projections
Intrinsic DP Guarantees of Randomized Algorithms
Do some randomized algorithms intrinsically enjoy
privacy guarantees?
Usually, we inject noise/randomness into an algorithm to get DP Guarantees
But many algorithms are already randomized!
Neighboring inputs =
exchange one entry in the stream
DP Guarantees of Stable Projections
\mathcal{M}(x) = Z^{\mathsf{T}}f(x)
What are the privacy guarantees of random projections when sketch size is 1?
\(p\)-stable random vector
\(p = 2\)
[Blocki, Blum, Datta, Sheffet ´12]
If \(\lVert f(x) \rVert_2^2 \geq 2 \log(1/\delta)/\varepsilon\) we get \((\varepsilon, \delta)\)-DP
\(p \in (0,1]\)
\(\mathcal{M}\) is \((\Theta(1/p),0 )\)-DP
Pure DP!
Guarantee blows up for \(p \to 0\)
Unclear accuracy guarantees
[Wang, Pinelis, Song 21']
DP Guarantees of \(p\)-Stable for Small \(p\)
Our results:
\((\varepsilon,0 )\)-DP guarantees even for \(p\) small
(Work in progress)
Follows from improving analysis of previous work
\mathcal{M}(x) = Z^{\mathsf{T}}f(x)
\(p\)-stable random vector
Can we do better if we allow \(\delta > 0\)?
If number of distinct elements \(\geq 1/ \varepsilon p \approx (\log n)/\varepsilon\)
\(\implies \mathcal{M}\) is \((\varepsilon,0)\)-DP
DP Guarantee:
Beyond \(\delta = 0\): Approximating the Density
Showing DP guarantees boils down to bounding the ratio of densities with different variances
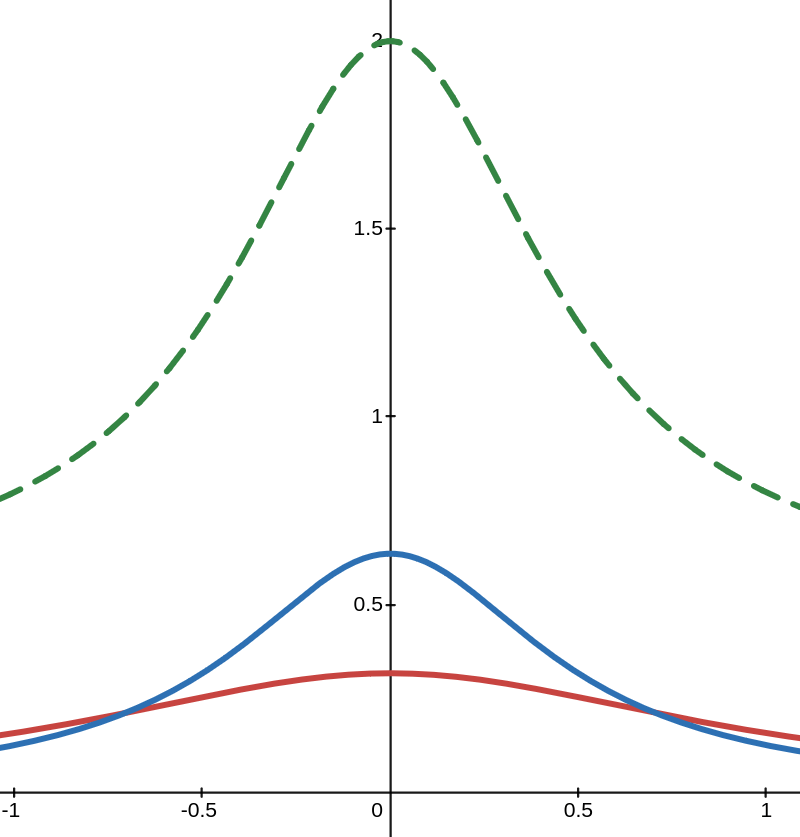
Issue: no closed form for the densities
Main tool: Careful non-asymptotic approximations to the density
const. \(\varepsilon\) unconditionally
constant \(\delta\)
[Emily's MSc Thesis]
\(p \lesssim 1/\lg n\)
\((12, \phantom{0.82})\)-DP
\(0.82\)
Looking at at limit \(p \to 0\)
Behavior at the limit is known:
|\mathcal{D}_{p}|^p \longrightarrow \frac{1}{\mathsf{Exp}(1)}
\((\varepsilon, 0)\)-DP if # distinct elements \(\geq 1/ \varepsilon p \approx (\log n)/\varepsilon\)
For p-stable
Thus, allowing \((\varepsilon, \delta)\)-DP instead of \((\varepsilon, 0)\)-DP may not give us much
p \to 0
DP Guarantee
"in the limit"
\((\varepsilon, \delta)\)-DP If # distinct elements \(\geq \log (1/\delta)/\varepsilon\)
\(\gtrsim \log (n)/\varepsilon\)
Summary
We maybe able to improve guarantees
but not by much
Details being worked on
Thanks!
Our results: If # distinct elements is not small, estimating with stable projections already satisfies Pure DP
Stable Projections are a classical and effective way to estimate \(F_p\) norms and approximate
distinct elements
[This study was financed, in part, by FAPESP, Brasil (2024/09381-1)]
Backup
An Example: Computing the Mean
Goal:
is small
\mathcal{M}
\((\varepsilon, \delta)\)-DP that approximates the mean:
Algorithm:
\displaystyle
\mathcal{M}(x) = \mathrm{Mean}(x) + Z
Gaussian or Laplace noise
X = (x_1, \dotsc, x_n)
x_i \in [-1,1]
with
\mathbb{E}\Big[\lvert \mathcal{M}(X) - \mathrm{Mean}(x)\rvert \Big]
A Peek Into the Analysis
Showing DP guarantees boils down to bounding the ratio of densities with different variances
\frac{\phantom{\mathcal{D}_{p,1}(\phantom{Z})}}{\mathcal{D}_{p, \Delta}(\phantom{Z})}
\mathcal{D}_{p,1}(\phantom{Z})
Z
Z
Privacy Loss =
Z \sim \mathcal{D}_p
Bounded with probability \(\delta\)
\implies
(\varepsilon, \delta)\text{-DP}
Issue: \(p\)-stable distributions don't have a closed form for the densities
Looking at at limit \(p \to 0\)
Behavior at the limit is known:
|\mathcal{D}_{p}|^p \longrightarrow \frac{1}{\mathsf{Exp}(1)}
\((\varepsilon, 0)\)-DP if # distinct elements \(\geq 1/ \varepsilon p \approx (\log n)/\varepsilon\)
For p-stable
Thus, allowing \((\varepsilon, \delta)\)-DP instead of \((\varepsilon, 0)\)-DP may not give us much
p \to 0
So, what DP guarantees can we get for a random projection using this distribution?
\Big(\frac{1}{\mathsf{Exp}(1)}\Big)^{1/p}
DP Guarantee:
\((\varepsilon, \delta)\)-DP If # distinct elements \(\geq \log (1/\delta)/\varepsilon\)
\(\gtrsim \log (n)/\varepsilon\)
2025 Brazilian Math Colloquium Talk
By Victor Sanches Portella
