Lower Bounds for Private Estimation of
Victor Sanches Portella
July 2, 2025
joint work with Nick Harvey (UBC)
under All Reasonable Parameter Regimes
Gaussian Covariance Matrices
ime.usp.br/~victorsp
Private Covariance Estimation
\displaystyle
x_1, x_2, \dotsc, x_n \sim \mathcal{N}(0, \Sigma)
\displaystyle
\Sigma \succ 0
Unknown Covariance Matrix
\displaystyle
X \in \mathbb{R}^{d \times n}
\((\varepsilon, \delta)\)-differentially private \(\mathcal{M}\) to estimate \(\Sigma\)
on \(\mathbb{R}^d\)
Goal:
Required even without privacy
Required even for \(d = 1\)
[Karwa & Vadhan '18]
Is this tight?
\((\varepsilon, \delta)\)-DP \(\mathcal{M}\) with accuracy
\displaystyle
n = \tilde O\Big(\frac{d^2}{\alpha^2} + \frac{\log(1/\delta)}{\varepsilon} + \frac{d^2}{\alpha \varepsilon}\Big)
\displaystyle
\mathbb{E}[\lVert\mathcal{M}(X) - \Sigma\rVert_F^2] \leq \alpha^2
samples
Known algorithmic results
with
(Output of \(\mathcal{M}(X)\) does not change much if switch one \(x_i\))
Our Results - New Lower Bounds
Theorem
For any \((\varepsilon, \delta)\)-DP algorithm \(\mathcal{M}\) such that
\displaystyle
\mathbb{E}\big[\lVert\mathcal{M}(X) - \Sigma\rVert_F^2\big] \leq \alpha^2 = O(d)
and
\displaystyle
\delta = O\Big( \frac{1}{n \ln n}\Big)
we have
\displaystyle
n = \Omega\Big(\frac{d^2}{\alpha\varepsilon}\Big)
Above 1/n, DP may not be meaningful
Previous
\displaystyle
n = \Omega\big(\tfrac{d^2}{\alpha\varepsilon}\big)
Lower Bounds
\displaystyle
\tilde{O}(\tfrac{1}{n})
\displaystyle
\delta
\displaystyle
O(1)
\displaystyle
O(d)
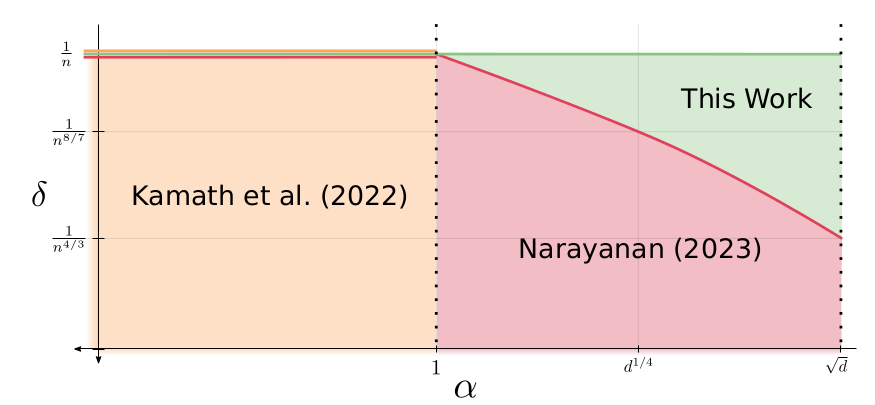
Accuracy \(\alpha^2\)
New Fingerprinting Lemma using
Stokes' Theorem
Follow up:
LBs for other problems
[Lyu & Talwar ´25]
Lower Bounds via Fingerprinting
Measures correlation between and
Correlation statistic
\displaystyle
\mathcal{C}(\phantom{z}, \phantom{\mathcal{M}(X)})
\displaystyle
\mathbb{E}[|\mathcal{C}(z, \mathcal{M}(X))|]
If \(z \sim \mathcal{N}(0, \Sigma)\) indep. of \(X\)
small
\displaystyle
\mathbb{E}[\mathcal{C}(x_i, \mathcal{M}(X))]
If \(\mathcal{M}\) is accurate
large
Fingerprinting Lemma
Approx. equal by privacy
Approx. equal by privacy
z
z
\mathcal{M}(X)
\mathcal{M}(X)
\displaystyle
\Sigma
\displaystyle
zz^{\intercal}
\displaystyle
zz^{\intercal}
\displaystyle
zz^{\intercal}
\displaystyle
zz^{\intercal}
\displaystyle
\mathcal{M}(X)
\displaystyle
\Sigma
\displaystyle
x_3 x_3^{\intercal}
\displaystyle
x_1 x_1^{\intercal}
\displaystyle
x_2 x_2^{\intercal}
\displaystyle
\mathcal{M}(X)
Example:
\displaystyle
\mathcal{C}(z, \mathcal{M}(X)) = \langle\mathcal{M}(X) - \Sigma, z z^{\intercal} - \Sigma \rangle
Randomizing \(\Sigma\)
To get a FP lemma, we need to randomize \(\Sigma\)
How to choose the distribution of \(\Sigma\)?
Narayanan (2023) drops independence with a Bayesian argument
otherwise, there is \(\mathcal{M}\) that knows \(\Sigma\) and ignores \(X\)
Most FP Lemma take independent coordinates
1 dim. FP Lemma and apply to each coord.
For covariance works only for high-accuracy \(\mathcal{M}\) (Kamath et al. 2022)
\displaystyle
\Bigg \{
Our idea: Many FP Lemmas use Stein's identity (Integration by parts)
How to do something similar in high-dimensions?
Score Statistic
\displaystyle
\mathcal{C}(z, \mathcal{M}(X)) = \big\langle\mathcal{M}(X) - \Sigma, \mathrm{Score}(z \;|\; \Sigma))\big\rangle
Gaussian Score function
Score Attack Statistic
First step: Pick a different correlation statistic
\displaystyle
\mathcal{C}(z, \mathcal{M}(X))
"Usual" choice
\displaystyle
\mathcal{C}(z, \mathcal{M}(X)) = \langle\mathcal{M}(X) - \Sigma, z z^{\intercal} - \Sigma \rangle
\displaystyle
zz^{\intercal}
\displaystyle
\mathcal{M}(X)
\displaystyle
\Sigma
[Cai et al. 2023]
\displaystyle
I
\displaystyle
\mathcal{M}(X)
\displaystyle
zz^{\intercal}
\displaystyle
\Sigma^{-1/2}
\displaystyle
\Sigma^{-1/2}
\displaystyle
\Sigma^{-1/2}
\displaystyle
\Sigma^{-1/2}
New Fingerprinting Lemma
\(\Sigma \sim\) Wishart leads to elegant analysis
Stein-Haff Identity
Want to "Move the derivative" with integration by parts
Stokes' Theorem
\displaystyle \sum_{j,k} \frac{\partial}{\partial \Sigma_{jk}} \mathbb{E}[\mathcal{M}(X) \; | \; \Sigma]
\displaystyle
\sum_{i} \mathcal{C}(x_i, \mathcal{M}(X)) =
Divergence of \(\Sigma \mapsto \mathbb{E}[\mathcal{M}(X) \; | \; \Sigma]\)
Large If \(\mathbb{E}[\mathcal{M}(X) \; | \; \Sigma]\approx \Sigma\)
Main property:
\displaystyle
= \int ( \mathrm{div} \, \mathbb{E}[\mathcal{M}(X) \; | \; \Sigma] )\, \phantom{p(\Sigma)} \mathrm{d}\Sigma
\displaystyle \mathbb{E}\;\Big[ \mathrm{div}\, \mathbb{E}[\mathcal{M}(X) \; | \; \Sigma] \Big]
\(\Sigma\) is random with density \(p\)
\displaystyle
p(\Sigma)
\displaystyle \Sigma \sim p
Summary
Our results
Score Attack Statistic
Tight lower bounds private covariance estimation
over a broad parameter regime
\displaystyle
\int ( \mathrm{div} \, \mathbb{E}[\mathcal{M}(X) \; | \; \Sigma] )\, \phantom{p(\Sigma)} \mathrm{d}\Sigma
\displaystyle
p(\Sigma)
\displaystyle
zz^{\intercal}
\displaystyle
\Sigma^{-1/2}
\displaystyle
\Sigma^{-1/2}
\displaystyle
I
\displaystyle
\mathcal{M}(X)
\displaystyle
\Sigma^{-1/2}
\displaystyle
\Sigma^{-1/2}
Stein-Haff Identify
Thanks!
Technical Secret Sauce:
New Fingerprinting Lemma
Lower Bounds for Private Estimation of
Victor Sanches Portella
July 2, 2025
joint work with Nick Harvey (UBC)
under All Reasonable Parameter Regimes
Gaussian Covariance Matrices
ime.usp.br/~victorsp
Randomizing \(\Sigma\)
To get a FP lemma, we need to randomize \(\Sigma\)
\(\Sigma\) with "small variance" \(\implies\)
FP Lemma only for high-accuracy \(\mathcal{M}\)
\(\Sigma\) with "large variance" \(\implies\)
hard to upper bound \(\mathbb{E}[|\mathcal{C}(z, \mathcal{M}(X))|]\) for independent \(z\)
\displaystyle
\mathbb{E}[\mathcal{C}(x_i, \mathcal{M}(X))]
If \(\mathcal{M}\) is accurate
large
Fingerprinting Lemma
\displaystyle
\Sigma
\displaystyle
x_3 x_3^{\intercal}
\displaystyle
x_1 x_1^{\intercal}
\displaystyle
x_2 x_2^{\intercal}
\displaystyle
\mathcal{M}(X)
\displaystyle
\mathcal{M}(X) = \mathbb{E}[\Sigma]
is accurate and ignores \(X\)
otherwise, there is \(\mathcal{M}\) that knows \(\Sigma\) and ignores \(X\)
Randomizing \(\Sigma\)
\displaystyle
I
\displaystyle
\mathcal{M}(X)
\displaystyle
zz^{\intercal}
\displaystyle
\Sigma^{-1/2}
\displaystyle
\Sigma^{-1/2}
\displaystyle
\Sigma^{-1/2}
\displaystyle
\Sigma^{-1/2}
\displaystyle
\int ( \mathrm{div} \, \mathbb{E}[\mathcal{M}(X) \; | \; \Sigma] )\, \phantom{p(\Sigma)} \mathrm{d}\Sigma
\displaystyle
p(\Sigma)
New Fingerprinting Lemma
\(\Sigma \sim\) Wishart leads to elegant analysis
Stein-Haff Identity
Want to "Move the derivative" with integration by parts
\displaystyle
= \int ( \mathrm{div} \, \mathbb{E}[\mathcal{M}(X) \; | \; \Sigma] )\, \phantom{p(\Sigma)} \mathrm{d}\Sigma
Stokes' Theorem
\displaystyle
\sum_{i = 1}^n \mathbb{E}[\mathcal{C}(x_i, \mathcal{M}(X))]
\displaystyle
\geq \Omega(d^2)
\displaystyle
O(n \alpha \varepsilon) \geq
FP Lemma
Upper Bound
\displaystyle \mathbb{E}\;\Big[ \mathrm{div}\, \mathbb{E}[\mathcal{M}(X) \; | \; \Sigma] \Big]
\(\Sigma\) is random with density \(p\)
\displaystyle
p(\Sigma)
\displaystyle \Sigma \sim p
Score Statistic
\displaystyle
\mathcal{C}(z, \mathcal{M}(X)) = \big\langle\mathcal{M}(X) - \Sigma, \mathrm{Score}(z \;|\; \Sigma))\big\rangle
Gaussian Score function
Score Attack Statistic
First step: Pick a different correlation statistic
\displaystyle
\mathcal{C}(z, \mathcal{M}(X))
"Usual" choice
\displaystyle
\mathcal{C}(z, \mathcal{M}(X)) = \langle\mathcal{M}(X) - \Sigma, z z^{\intercal} - \Sigma \rangle
\displaystyle
zz^{\intercal}
\displaystyle
\mathcal{M}(X)
\displaystyle
\Sigma
\displaystyle \sum_{j,k} \frac{\partial}{\partial \Sigma_{jk}} \mathbb{E}[\mathcal{M}(X) \; | \; \Sigma]
\displaystyle
\sum_{i} \mathcal{C}(x_i, \mathcal{M}(X)) =
Divergence of \(\Sigma \mapsto \mathbb{E}[\mathcal{M}(X) \; | \; \Sigma]\)
Large If \(\mathbb{E}[\mathcal{M}(X) \; | \; \Sigma]\approx \Sigma\)
Main property:
\displaystyle
I
\displaystyle
\mathcal{M}(X)
\displaystyle
zz^{\intercal}
\displaystyle
\Sigma^{-1/2}
\displaystyle
\Sigma^{-1/2}
\displaystyle
\Sigma^{-1/2}
\displaystyle
\Sigma^{-1/2}
COLT 2025 Talk
By Victor Sanches Portella
