Векторная алгебра
11 класс
vkrysanov320@gmail.com
version 4.1 not-fixed, 16-01-2024Понятие вектора
Вектором называется направленный отрезок.
B
A
\overline{a}
Если даны начало вектора (точка ) и его конец (точка ), то вектор обозначается . Также обозначается малыми латинскими буквами с чертой сверху: или жирным шрифтом: .
\overline{AB}
A
B
\mathbf{a}
\overline{a}
Нуль-вектором называется вектор, у которого конец совпадает с началом, обозначается: или . Можно считать, что нуль-вектор имеет любое желаемое в данный момент направление.
\mathbf{0}
\overline{0}
\overline{a}
Модулем вектора называется его длина. Модуль вектора обозначается .
|\overline{a}|
Очевидно, что .
|\overline{0}| = 0
Основные определения вектора
\overline{a}
Векторы и называются сонаправленными, если они коллинеарны и направлены в одну сторону. Обозначается:
\overline{b}
\overline{a} \upuparrows \overline{b}.
\overline{a}
Векторы и называются противоположными, если они коллинеарны и направлены в разные стороны. Обозначается:
\overline{b}
\overline{a} \uparrow \downarrow \overline{b}.
\overline{a}
Векторы и называются коллинеарными, если они расположены на параллельных прямых или на одной прямой. Обозначается:
\overline{b}
\overline{a} \parallel \overline{b}.
\overline{a}
Векторы и называются равными, если они сонаправлены и имеют одинаковую длину. Обозначается:
\overline{b}
\overline{a} = \overline{b}.
\overline{a}
\overline{b}
\overline{a}
\overline{b}
\overline{a}
\overline{b}
\overline{a}
\overline{b}
Линейные операции над векторами
*Линейными называют операции сложения, вычитания векторов и умножения вектора на число
Сложение векторов
\overline{a} + \overline{b}
Суммой двух векторов называется вектор, полученный:
- по правилу «треугольника»: второй вектор откладывается так, чтобы его начало совпадало с концом первого вектора :
\overline{a}
\overline{b}
\overline{b}
\overline{a}
\overline{a} + \overline{b}
Суммой будет являться «замыкающий» вектор , начало которого совпадает с началом первого вектора , а конец — с концом второго вектора .
\overline{a} + \overline{b}
\overline{a}
\overline{b}
- по правилу «параллелограмма»: второй вектор откладывается из начала первого вектора , на этих векторах строится параллелограмм и суммой в этом случае является диагональ этого параллелограмма.
\overline{b}
\overline{a}
\overline{a} + \overline{b}
\overline{a}
\overline{b}
\overline{a} + \overline{b}
\overline{b}
\overline{a}
Сложения векторов. Свойства
\overline{a} + \overline{b} = \overline{b} + \overline{a}.
1. Коммутативный закон сложения:
(\overline{a} + \overline{b}) + \overline{c} = \overline{a} + (\overline{b} +\overline{c}).
2. Ассоциативный закон сложения:
3.
\overline{a} + \overline{0} = \overline{a}.
Разность векторов
\overline{a} - \overline{b}
Разностью двух векторов называется сумма вектора векторов и противоположного к :
\overline{a}
\overline{a} - \overline{b} = \overline{a} + (- \overline{b}).
\overline{a}
\overline{b}
Противоположным к вектору называется такой вектор, что его сумма с равна нуль-вектору. Обозначается
\overline{a}
-\overline{a}: -\overline{a} + \overline{a} = \overline{0}.
Одним из векторов будет, например, такой, что его начало совпадает с концом вектора , а конец с началом .
-\overline{a}
\overline{a}
\overline{a}
\overline{a}
-\overline{a}
\overline{a}
\overline{b}
\overline{a} + \overline{b}
\overline{a} - \overline{b}
-\overline{b}
Строим противоположный к вектор, «переворачивая» его в противоположную сторону и, откладывая его от конца вектора , строим сумму векторов и .
\overline{b}
\overline{a}
\overline{a}
-\overline{b}
Умножение вектора на число
\lambda
Произведением вектора на действительное число называется вектор , коллинеарный вектору , имеющий длину сонаправленный с , если , и противонаправленный с , если
\overline{a}
\overline{c}
\overline{a}
|\overline{c}| = |\lambda| \cdot |\overline{a}|
\overline{a}
\lambda > 0
\overline{a}
\lambda < 0.
Противоположный вектор можно рассматривать как результат умножения вектора на число
-\overline{a}
\lambda = -1: -\overline{a} = (-1)\overline{a}.
\overline{a}
\overline{a}
2\overline{a}
\frac{1}{2}\overline{a}
-\frac{1}{2}\overline{a}
Легкие задачки...
2. Найти угол между векторами и , если вектор их разности образует с ними углы и .
40^{\circ}
\overline{a}
\overline{b}
|\overline{a} + \overline{b} + \overline{c} + \overline{d} |
60^{\circ}
1. Найти .
\overline{a}
\overline{b}
\overline{c}
\overline{d}
\overline{a} - \overline{b}
3. Человек хочет переплыть реку так, чтобы оказаться на другом ее берегу строго напротив того места, где он зашёл в воду. Под каким углом к берегу ему необходимо плыть, если его скорость относительно воды в два раза больше скорости течения реки?
Легкие задачки. Решение
\overline{a}
\overline{b}
\overline{a} - \overline{b}
40^{\circ}
60^{\circ}
\varphi = 180^\circ - 40^\circ - 60^\circ = 80^\circ.
\varphi
|\overline{a} + \overline{b} + \overline{c} + \overline{d} |
1. Найти .
\overline{a}
\overline{b}
\overline{c}
\overline{d}
\overline{b}
\overline{c}
\overline{d}
* Осуществляется параллельный перенос для выполнения правил сложнее векторов. Искомый вектор — пурпурный.
\Rightarrow |\overline{a} + \overline{b} + \overline{c} + \overline{d} | = 1.
2. Найти угол между векторами и , если вектор их разности образует с ними углы и .
40^{\circ}
\overline{a}
\overline{b}
60^{\circ}
\overline{a} - \overline{b}
3. Человек хочет переплыть реку так, чтобы оказаться на другом ее берегу строго напротив того места, где он зашёл в воду. Под каким углом к берегу ему необходимо плыть, если его скорость относительно воды в два раза больше скорости течения реки?
\overline{v_1}
\overline{v_1} + \overline{v_2}
\overline{v_2}
\overline{v_2}
|\overline{v_1} + \overline{v_2}| = 2|\overline{v_1}|
|\overline{v_1} |
2|\overline{v_1}|
\varphi
A
B
C
D
30^{\circ}
\Rightarrow \varphi = 60^\circ
* из условия
Еще одна простая задачка...
4. Самолёт пролетел сначала 5 км на северо-запад, а потом 10 км на во-сток. На каком расстоянии от начала своего движения он оказался?
* пренебречь шарообразной формой Земли, то есть можно считать ее плоской при перемещениях на небольшие расстояния.
Еще одна простая задачка. Решение
4. Самолёт пролетел сначала 5 км на северо-запад, а потом 10 км на во-сток. На каком расстоянии от начала своего движения он оказался?
* пренебречь шарообразной формой Земли, то есть можно считать ее плоской при перемещениях на небольшие расстояния.
\overline{p_{NW}}
\overline{p_{E}}
\overline{p}
5
10
45^{\circ}
N
|\overline{p}| = \sqrt{|\overline{p_{NW}}|^2 + |\overline{p_{E}}|^2 - 2 \cdot |\overline{p_{NW}}| \cdot |\overline{p_{E}}|
\cdot \cos \angle(\overline{p_{NW}}; \overline{p_{E}})}
= \sqrt{5^2 + 10^2 - 2 \cdot 5 \cdot 10 \cdot \cos 45^\circ} =
\sqrt{125 - 50 \cdot \sqrt{2}}.
Решение:
Ответ:
\sqrt{125 - 50 \cdot \sqrt{2}}.
Задача 1
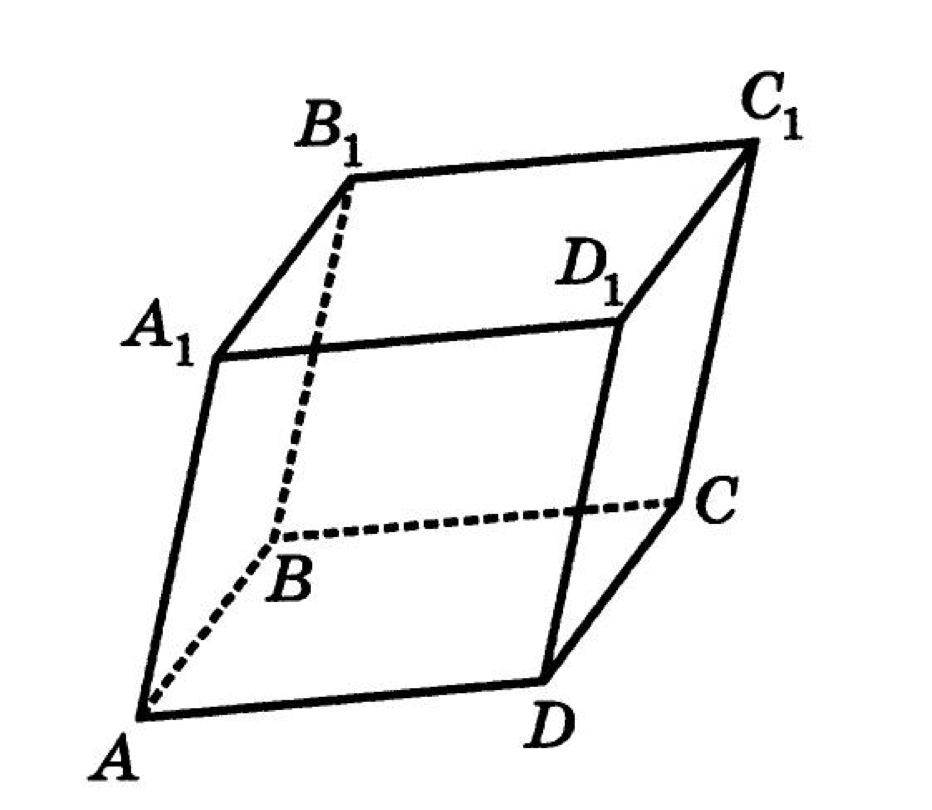
Пусть — параллелепипед. Найти алгебраическую сумму векторов:
ABCDA_1B_1C_1D_1
\overline{AB} + \overline{AD} - \overline{AA_1};
1.
2.
3.
4.
5.
\overline{AB} - \overline{AD} + \overline{AA_1};
-\overline{AB} - \overline{AD} + \overline{AA_1};
\overline{AB} - \overline{AD} - \overline{AA_1};
-\overline{AB} + \overline{AD} - \overline{AA_1}.
Задача 1. Решение
Пусть — параллелепипед. Найти алгебраическую сумму векторов:
ABCDA_1B_1C_1D_1
\overline{AB} + \overline{AD} - \overline{AA_1} = \overline{AC} - \overline{AA_1} = \overline{A_1C};
1.
2.
3.
4.
5.
\overline{AB} - \overline{AD} + \overline{AA_1} = \overline{DB} + \overline{AA_1} =
-\overline{AB} - \overline{AD} + \overline{AA_1} = \overline{CA} + \overline{AA_1} =
\overline{AB} - \overline{AD} - \overline{AA_1} = \overline{DB} - \overline{DD_1} = \overline{D_1B};
-\overline{AB} + \overline{AD} - \overline{AA_1}= \overline{BD} - \overline{AA_1} = \overline{BD} - \overline{BB_1} = \overline{B_1D}.
= \overline{CA_1};
= \overline{DB} + \overline{BB_1} = \overline{DB_1};
Задача 2
Дан куб . Выразить данную алгебраическую сумму векторов через вектор, начало и конец которого есть вершины куба.
ABCDA_1B_1C_1D_1
\overline{a} + \overline{b} - \overline{c};
1.
2.
3.
4.
5.
\overline{a} - \overline{b} + \overline{c};
\overline{a} + \overline{b} - \overline{c};
-\overline{a} + \overline{b} - \overline{c};
-\overline{a} + \overline{b} + \overline{c}.
\overline{B_1A_1} = \overline{a}, \overline{B_1B} = \overline{b}, \overline{B_1C_1} = \overline{c},
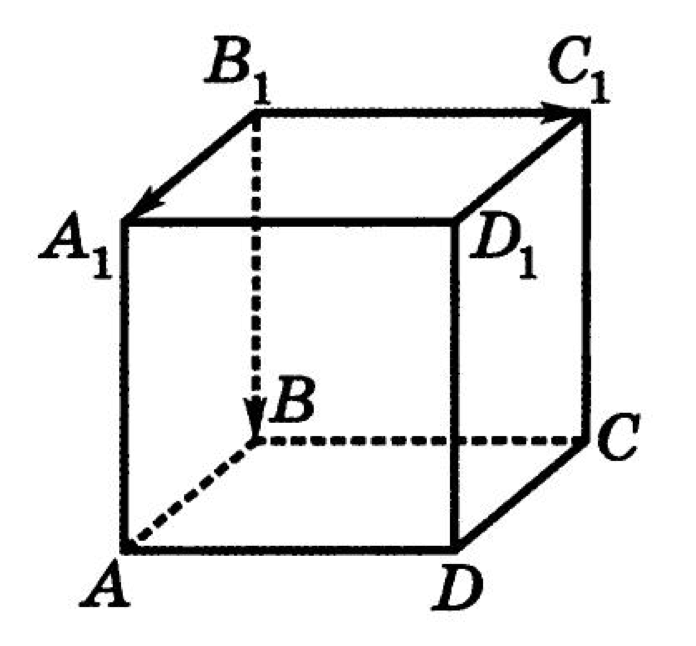
где — общее начало данных векторов.
B_1
базисные векторы
* Базис — упорядоченный (конечный или бесконечный) набор векторов в векторном пространстве, такой, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого набора. Векторы базиса называются базисными векторами.
Задача 3
В параллелепипеде точки — середины ребер. Пусть
ABCDA_1B_1C_1D_1
\overline{K_3T_1};
\overline{AA_1} = \overline{a}, \overline{AB} = \overline{b}, \overline{AD} = \overline{c}
P_1, P_2, ..., P_4, K_1, K_2, ... K_4
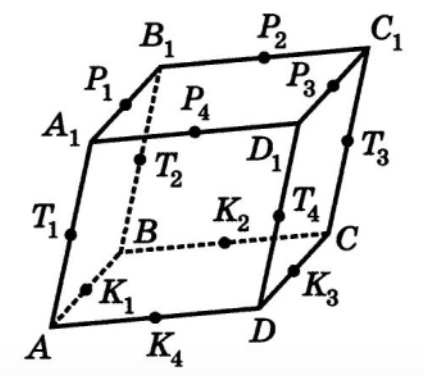
— базисные векторы.
\overline{a}, \overline{b}, \overline{c}
1. Выразить заданные векторы через базисные ( ):
a)
\overline{DP_1};
б)
\overline{P_2K_3};
в)
\overline{A_1K_2};
г)
\overline{T_4K_1}.
д)
2. Доказать, что:
\overline{P_2K_3} = \overline{P_1K_4};
a)
\overline{K_1P_2} = \overline{K_4P_3};
б)
\overline{P_1T_3} = \overline{T_1K_3};
в)
\overline{K_1C_1} = \overline{AP_3};
г)
2\overline{T_2P_2} = \overline{K_1P_3}.
д)
Скалярное произведение векторов
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:
\overline{a} \cdot \overline{b} = |\overline{a}| \cdot |\overline{b}| \cdot \cos\angle(\overline{a}; \overline{b}).
Следствие I: Для ненулевые векторов и :
\overline{a}
\overline{b}
\overline{a} \upuparrows \overline{b}
\overline{a} \cdot \overline{b} = |\overline{a}| \cdot |\overline{b}| .
если , то
\overline{a} \cdot \overline{b} = -|\overline{a}| \cdot |\overline{b}| .
если , то
\overline{a} \uparrow \downarrow \overline{b}
\overline{a} \cdot \overline{b} = |\overline{a}|^2
если , то , тогда
\overline{a} = \overline{b}
Следствие II: Для ненулевые векторов и :
\overline{a}
\overline{b}
\cos\angle(\overline{a}; \overline{b}) = \frac{\overline{a} \cdot \overline{b}}{|\overline{a}| \cdot |\overline{b}|}.
Теорема: Для того, чтобы два ненулевых вектора были взаимно перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение равнялось нулю.
|\overline{a}| = \sqrt{\overline{a}^2}.
Скалярное произведение векторов. Св-ва
\overline{a} \cdot \overline{b} = \overline{b} \cdot \overline{a}.
1. Коммутативность:
(\lambda \cdot \overline{a}) \cdot \overline{b} = \lambda(\overline{a} \cdot \overline{b}).
2. Ассоциативный закон умножения:
3. Дистрибутивность относительно сложения и умножения векторов:
(\overline{a} + \overline{b}) \cdot \overline{c} = \overline{a}\cdot\overline{c} + \overline{b}\cdot\overline{c}.
4. ; Если , то .
\overline{a}^2 \ge 0
\overline{a} \ne 0
\overline{a}^2 > 0
Задача 1
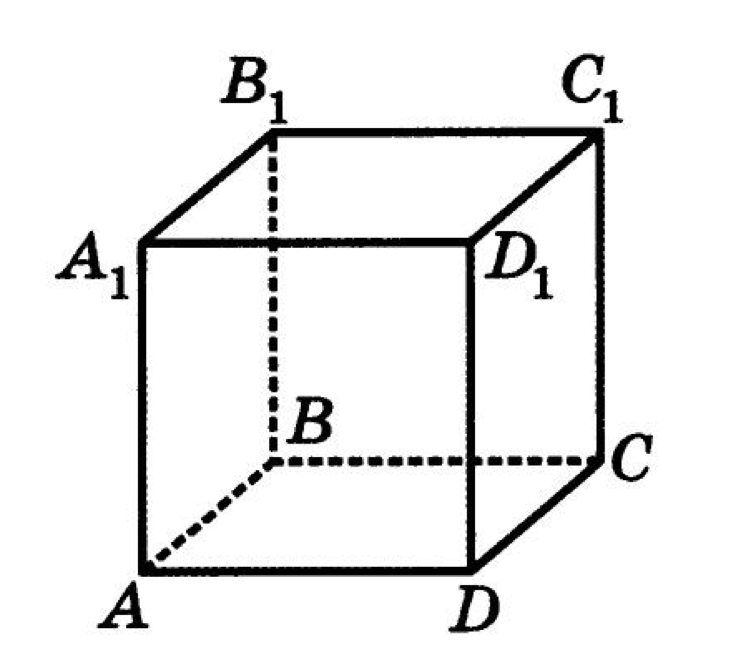
Дан куб со стороной . Базисные векторы
ABCDA_1B_1C_1D_1
Найти:
t
\overline{AA_1} = \overline{a}, \overline{AB} = \overline{b}, \overline{AD} = \overline{c},
|\overline{a}| = |\overline{b}| = |\overline{c}| = t, \angle(\overline{a}, \overline{b}) = \angle(\overline{a}, \overline{c}) =
\angle(\overline{c}, \overline{b}) = 90^\circ.
где
\overline{AB_1} \cdot \overline{BC};
1.
2.
3.
4.
5.
\overline{CD_1} \cdot \overline{AC_1};
\angle(\overline{DC_1} ; \overline{CB_1});
\angle(\overline{A_1C} ; \overline{D_1B_1});
\rho(A_1D ; AB_1).
Задача 2
Дан правильная треугольная пирамида , все ребра которой равны между собой. Известно, что — середины ребер. Базисные векторы:
и
DABC
Найти:
P, K, N, M
|\overline{a}| = |\overline{b}| = |\overline{c}| = t,
\angle(\overline{a}, \overline{b}) = \angle(\overline{a}, \overline{c}) =
\angle(\overline{c}, \overline{b}) = 60^\circ.
1.
2.
3.
\angle(\overline{AD} ; \overline{CB});
\angle(\overline{CP} ; \overline{AK});
\rho(CP ; AK).
|\overline{AD}| = |\overline{a}|,
|\overline{AB}| = |\overline{b}|,
|\overline{AC}| =|\overline{c}|,
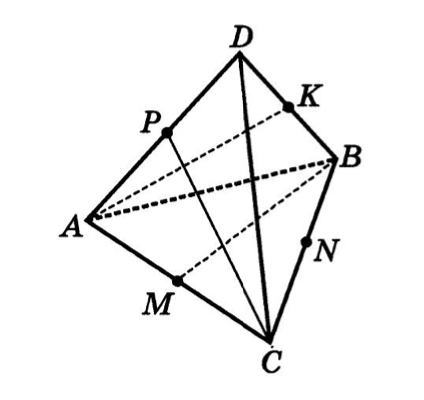
Задача 3
— пирамида, все ребра которой равны .
SABC
m
\overline{AS} = \overline{a},
\overline{AB} = \overline{b},
\overline{AD} = \overline{c}
1.
2.
\rho(K_4T_4; K_3T_3);
\angle(\overline{T_4A} ; \overline{DT_3}).
T_1, T_2, T_3, T_4, K_5, K_2, K_3, K_4
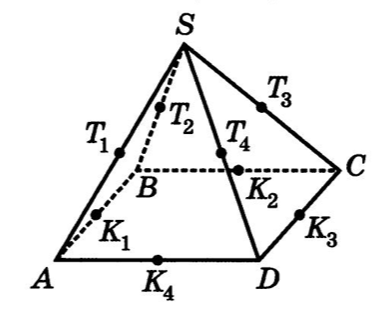
— середины ребер. Полагая, что , найти:
Координатно-векторный метод
Прямоугольная система координат в пространстве
x
y
z
абсцисса
ордината
аппликата
O
Если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление (оно обозначается стрелкой) и выбрана единица измерения отрезков, то говорят, что задана прямоугольная система координат в пространстве.
M(x_0; y_0; z_0)
Разложение вектора на составляющие по осям координат
x
y
z
O
\overline{j}
\overline{i}
\overline{k}
\overline{a}
M
P
M_2
M_1
M_3
— единичный вектор по оси
\overline{i}
— единичный вектор по оси
\overline{j}
— единичный вектор по оси
\overline{k}
Ox
Oy
Oz
|\overline{i}| = |\overline{j}| = |\overline{k}| = 1.
три единичных вектора (орты), образуют декартов ортогональный базис.
\overline{a} = a_x \cdot |\overline{i}| + a_y \cdot |\overline{j}| + a_z \cdot |\overline{k}|
Ф-ла разложения вектора на составляющие по осям координат
\overline{a} = \{a_x; a_y; a_z \}
Основные теоремы
Напоминание: Пусть Тогда:
\overline{a}\{x_1; y_1; z_1\},
\overline{b}\{x_2; y_2; z_2\}.
k\overline{a}\{x_1; y_1; z_1\} = \{kx_1; ky_1; kz_1\};
\overline{a}\{x_1; y_1; z_1\}+
\overline{b}\{x_2; y_2; z_2\}=
\{x_1+x_2; y_1+y_2; z_1+z_2\};
|\overline{a}|
= \sqrt{x_1^2 + y_1^2 + z_1^2}.
* Если известны координаты вектора, то линейные операции над векторами можно заменить соответствующими арифметическими действиями над координатами
Скалярное произведение векторов в координатной форме на плоскости
\overline{a}(x_1; y_1), \overline{b}(x_2; y_2)
Теорема: Для векторов, записанных в координатной форме на плоскости — , верно равенство:
\overline{a} \cdot \overline{b} = x_1 \cdot x_2 + y_1 \cdot y_2.
Следствие I: Если , то , тогда
\overline{a} = \overline{b}
\overline{a}^2 = x_1^2 + y_1^2
|\overline{a}| = \sqrt{x^2_1 + y^2_1}.
Следствие II: Если , тогда
\overline{a} \ne 0, \overline{b} \ne 0, \overline{a} \perp \overline{b}
x_1 \cdot x_2 + y_1 \cdot y_2 = 0.
Следствие III: Для :
\overline{a} \ne 0, \overline{b} \ne 0
\cos\angle(\overline{a}; \overline{b}) =
\frac{x_1\cdot x_2 + y_1 \cdot y_2}{\sqrt{x^2_1 + y^2_1} \cdot \sqrt{x^2_2 + y^2_2}}.
Скалярное произведение векторов в координатной форме в пространстве
\overline{a}(x_1; y_1, z_1), \overline{b}(x_2; y_2, z_2)
Теорема: Для векторов, записанных в координатной форме в пространстве — , верно равенство:
\overline{a} \cdot \overline{b} = x_1 \cdot x_2 + y_1 \cdot y_2 + z_1 \cdot z_2.
Следствие I: Если , то , тогда
\overline{a} = \overline{b}
\overline{a}^2 = x_1^2 + y_1^2 + z_1^2
|\overline{a}| = \sqrt{x^2_1 + y^2_1 + z^2_1}.
Следствие II: Если , тогда
\overline{a} \ne 0, \overline{b} \ne 0, \overline{a} \perp \overline{b}
x_1 \cdot x_2 + y_1 \cdot y_2 + z_1 \cdot z_2= 0.
Следствие III: Для :
\overline{a} \ne 0, \overline{b} \ne 0
\cos\angle(\overline{a}; \overline{b}) =
\frac{x_1\cdot x_2 + y_1 \cdot y_2 + z_1 \cdot z_2}{\sqrt{x^2_1 + y^2_1 + z^2_1} \cdot \sqrt{x^2_2 + y^2_2 + z^2_2}}.
Задача
Дано:
Найти
\overline{a}\{-2; 1; -1\},
\overline{b}\{1; -3; 2\}.
|\overline{a} + 2\overline{b}|
.
Задача. Решение
Дано: Найти
\overline{a}\{-2; 1; -1\},
\overline{b}\{1; -3; 2\}.
|\overline{a} + 2\overline{b}|
.
2\overline{b} = \{2\cdot1; 2\cdot(-3); 2\cdot 2 \}
= \{2; -6; 4\};
\overline{a} + 2\overline{b} = \{-2 + 2; 1-6; -1 + 4\}
= \{0; -5; 3\};
|\overline{a} + 2\overline{b}| = \sqrt{0^2 + (-5)^2 + 3^2} = \sqrt{34}.
Ответ:
\sqrt{34}.
Коллинеарные векторы
Два ненулевых вектора называются коллинеарными, если с точностью до параллельного переноса их можно одновременно разместить на одной прямой. Обозначение:
Теорема: Два ненулевых вектора и являются коллинеарными тогда и только тогда, когда существует число , такое, что или когда пропорциональны их координаты.
\overline{a}
\overline{b}
k \ne 0
\overline{a} = k\overline{b},
\overline{a} \upuparrows \overline{b}.
\overline{a}
\overline{b}
Задача
Коллинеарны ли векторы
\overline{a}\{3;1;4\},
\overline{b}\{-3;-1;-4\}?
Задача. Решение
Коллинеарны ли векторы
\overline{a}\{3;1;4\},
\overline{b}\{-3;-1;-4\}?
\overline{a} = k\overline{b} \Rightarrow
\overline{a}\{3;1;4\} = k\overline{b}\{-3;-1;-4\} \Rightarrow
\Rightarrow
\overline{a}\{3;1;4\} = \overline{b'}\{-3k;-1k;-4k\}
\Rightarrow
\begin{cases}
-3k = 3;\\
-k=1;\\
-4k=4;
\end{cases}
\Rightarrow k = -1.
Из этого следует, что векторы коллинеарны.
Решение:
Компланарные векторы
Три ненулевые вектора называются компланарными, если с точностью до параллельного переноса их можно одновременно разместить в одной плоскости.
B_1
\overline{a}
\overline{b}
D
C
B
O
A
E
\overline{c}
Теорема: Для того, чтобы три ненулевых вектора , , и были компланарны, необходимо и достаточно, чтобы существовала пара чисел и , таких, что и
\overline{a}
\overline{b}
\overline{c}
x
y
xy \ne 0
\overline{c} = x\overline{a} + y\overline{b}.
Какие векторы компланарные?
Задача
Компланарны ли векторы
\overline{a}\{1;-3;2\},
\overline{b}\{4;2;-2\},
\overline{c}\{-3;-5;3\}?
Задача. Решение
Компланарны ли векторы
\overline{a}\{1;-3;2\},
\overline{b}\{4;2;-2\},
\overline{c}\{-3;-5;3\}?
Решение:
\overline{c} = x\overline{a} + y\overline{b},
Пусть т.е.
x\overline{a} = \{1;-3;2\} = \overline{a'} \{x;-3x;2x\}
y\overline{b} = \{4;2;-2\} = \overline{b'}\{4y;2y;-2y\};
\Rightarrow
x\overline{a} + y\overline{b} = \overline{c'}\{x+4y;-3x+2y;2x-2y\} = \overline{c}\{-3;-5;3\}.
\Rightarrow \begin{cases}
x+4y=-3;\\
-3x+2y=-5;\\
2x-2y;
\end{cases}
\Rightarrow \begin{cases}
x+4y=-3;\\
-x=-2;\\
2x-2y;
\end{cases}
\Rightarrow \begin{cases}
4y=-5;\\
x=2;\\
2y=1;
\end{cases}
\Rightarrow \begin{cases}
y=-1{,}25;\\
x=2;\\
y = 0{,}5;
\end{cases}
\Rightarrow \varnothing
Таких чисел не существует, следовательно векторы не компланарны.
Разложение вектора по трем некопланарным векторам
Если вектор представлен в виде , где — некоторые числа, говорят, что вектор разложен по векторам Числа называются коэффициентами разложения.
\overline{q}
\overline{q} = x\overline{a} + y\overline{b} + z\overline{c}
x,y,z
\overline{q}
\overline{a}, \overline{b}, \overline{c}.
x,y,z
Теорема: Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.
Задача
Разложить вектор
\overline{n}\{1;-1;2\}
по трем некомпланарным векторам
\overline{a}\{-2;1;-1\}, \overline{b}\{1;-3;2\}, \overline{c}\{2;-3;0\}.
Задача. Решение
Разложить вектор
\overline{n}\{1;-1;2\}
по трем некомпланарным векторам
\overline{a}\{-2;1;-1\}, \overline{b}\{1;-3;2\}, \overline{c}\{2;-3;0\}.
Решение:
Так как векторы некомпланарны, то существуют числа , не равные нулю, такие, что
\overline{a}, \overline{b}, \overline{c}
x,y,z
\overline{n} = x\overline{a} + y\overline{b} + z\overline{c}.
\Rightarrow \begin{cases}
1 = -2x + y + 2z;\\
-1 = x - 3y - 3z;\\
2 = -x + 2y + 0z;
\end{cases}
\Rightarrow \begin{cases}
-5y - 4z = -1;\\
-y - 3z = 1;\\
-x + 2y = 2;
\end{cases}
\Rightarrow \begin{cases}
11z = -6;\\
-y - 3z = 1;\\
-x + 2y = 2;
\end{cases}
\Rightarrow \begin{cases}
z = -\frac{6}{11};\\
y = \frac{7}{11};\\
x = -\frac{8}{11}.
\end{cases}
\Rightarrow \overline{n} = -\frac{8}{11}\overline{a} +
\frac{7}{11}\overline{b} -
\frac{6}{11}\overline{c}.
Задача (на дом)
\triangle ABC
В вершины имеют координаты . Найти:
A(0;2;-1), B(2;0;1), C(4;2;-2)
1. Длину медианы
2. Угол
3. Координаты точки , если — параллелограмм.
m_{AC} = BM;
C;
D
ABCD
Деление отрезка в данном отношении
Отрезок определен своими концами
Если делит делит отрезок в отношении тогда координаты точки вычисляются по следующему принципу:
M_1M_2
M_1(x_1;y_1; z_1), M_2(x_2;y_2; z_2).
M
M_1M_2
\frac{M_1M}{MM_2} = \lambda
M
M(\frac{x_1 + \lambda x_2}{1+\lambda}; \frac{y_1 + \lambda y_2}{1+\lambda}; \frac{z_1 + \lambda z_2}{1+\lambda}).
Пример: Даны точки Найти координаты точки — середины .
Решение:
M_1(1;2;3), M_2(2;1;1).
M
M_1M_2
\frac{M_1M}{MM_2} = \lambda = 1 \Rightarrow M(\frac{1 + 1 \cdot 2}{1+1}; \frac{2 + 1 \cdot 1}{1+1}; \frac{3 + 1 \cdot 1}{1+1})
\Rightarrow M(1{,}5; 1{,}5; 2).
Расстояние между двумя точками
d(M_1; M_2) = |\overline{M_1M_2}| = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2 + (z_2 - z_1)^2}
y
z
O
M_2
M_1
параллельный перенос
Задача 1
ABCDEFA_1B_1C_1D_1E_1F_1
В правильной шестиугольной призме отношение длин ребер, исходящих из одной вершины, равно , где — наибольшее ребро. Точки — середины, соответственно, ребер Найти:
1) ;
2) ;
3) ;
4) ;
3:2:2
AA_1
N, K, T, P
B_1C_1, D_1E_1, CD, FE.
\angle(PD_1; DN)
\rho(D; FA_1)
\rho(FE_1; EB_1).
\angle(FA_1; AB_1)
\angle(NT; PK)
\angle(TF_1; BK)
5) ;
6)
Задача 2
ABCDEFA_1B_1C_1D_1E_1F_1
В правильной шестиугольной призме отношение длин ребер, исходящих из одной вершины, равно , где — наибольшее ребро. Точки — середины, соответственно, ребер Найти:
1) ;
2) ;
3) ;
4) ;
3:2:2
AA_1
N, K, T, P
B_1C_1, D_1E_1, CD, FE.
\angle(PD_1; DN)
\rho(D; FA_1)
\rho(FE_1; EB_1).
\angle(FA_1; AB_1)
\angle(NT; PK)
\angle(TF_1; BK)
5) ;
6)
Уравнение плоскости
Пусть задана прямоугольная система координат и дана некоторая поверхность , например плоскость. Уравнение с тремя переменными называется уравнением поверхности , если этому уравнению удовлетворяют координаты любой точки поверхности и не удовлетворяют координаты никакой точки, не лежащей на этой поверхности.
F
Oxyz
x,y,z
F
F
\overline{n}\{A;B;C\}
M_0(x_0; y_0;z_0)
M(x; y;z)
\alpha
\overline{n} \perp \alpha
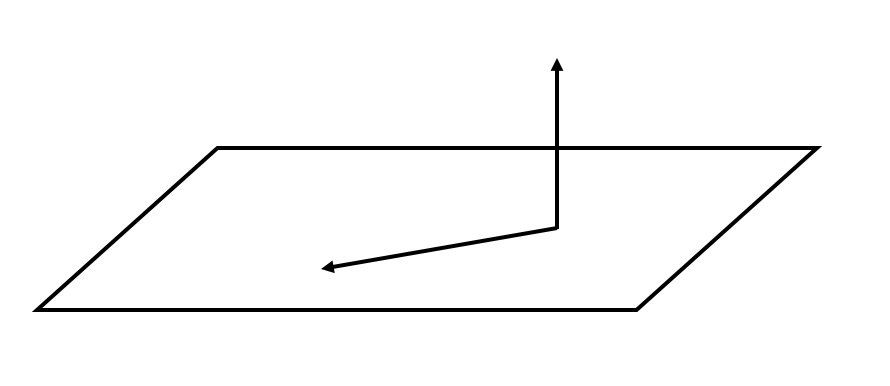
, где
\overline{n}\{A;B;C\}
M_0 \in \alpha
M \in \alpha
, где
, где
M_0(x_0; y_0;z_0)
M(x; y;z)
Уравнение плоскости (2)
\overline{n}\{A;B;C\}
M_0(x_0; y_0;z_0)
M(x; y;z)
\alpha
\overline{n} \perp \alpha
, где
\overline{n}\{A;B;C\}
M_0 \in \alpha
M \in \alpha
, где
, где
M_0(x_0; y_0;z_0)
M(x; y;z)
\Rightarrow
\overline{M_0M} = \{x-x_0;y-y_0;z-z_0\}
причем
\overline{n} \cdot \overline{M_0M} = 0 (\overline{n} \perp \alpha)
\Rightarrow
A(x-x_0) + B(y-y_0) + C(z-z_0) = 0
Уравнение плоскости, которой принадлежит точка
M_0(x_0; y_0;z_0)
Ax + By + Cz - (Ax_0 + By_0 + Cz_0) = 0
D
Ax + By + Cz + D = 0
Общий вид уравнения плоскости:
Задача 1
N_1(1;1;-1),
N_2(2;-1;1),
N_3(-1;1;1)
\Rightarrow -\frac{2}{3}Dx - Dy - \frac{2}{3}Dz + D = 0; (\cdot 3) (: (-D))
Точки принадлежат плоскости . Написать уравнение данной плоскости.
\alpha
\begin{cases}
Ax_1 + By_1 + Cz_1 + D = 0;\\
Ax_2 + By_2 + Cz_2 + D = 0;\\
Ax_3 + By_3 + Cz_3 + D = 0;
\end{cases}
\Rightarrow
\begin{cases}
A + B - C + D = 0;\\
2A - B + C + D = 0; 2 \cdot(1) - (2)\\
-A + B + C + D = 0; (1) + (3)
\end{cases}
\Rightarrow
\begin{cases}
A + B - C + D = 0;\\
0 + 3B - 3C + D = 0; \\
0 + 2B + 0 + 2D = 0;
\end{cases}
Составим систему трех уравнений с тремя неизвестными, используя уравнение плоскости и подставляя в него координаты данных точек:
\Rightarrow
\begin{cases}
A + B - C + D = 0;\\
-3D - 3C + D = 0; \\
B = -D;
\end{cases}
\Rightarrow
\begin{cases}
A = -\frac{2}{3}D;\\
B = -D;\\
C = -\frac{2}{3}D.
\end{cases}
\Rightarrow 2x + 3y + 2z - 3 = 0.
Решение:
Задача 2
A(1;2;-7)
Найти расстояние от точки до плоскости , заданной уравнением .
\alpha
12x + 4y + 3z - 4 = 0
M_0
A
\overline{n}
\alpha
Решение:
Из условия задачи следует, что .
\overline{n}\{12;4;3\}
\overline{AM_0} \parallel \overline{n}, M_0 \in \alpha, M_0(x_0; y_0; z_0)
\Rightarrow \overline{AM_0}\{x_0-1; y_0-2; z_0+7\}.
\overline{AM_0} \parallel \overline{n}
Т.к. , то существует
такое , что . Значит:
p \ne 0
\overline{AM_0} = p\overline{n}
\begin{cases}
x_0 - 1 = 12p;\\
y_0 - 2 = 4p;\\
z_0 + 7 = 3p;
\end{cases}
\Rightarrow
\begin{cases}
x_0 = 12p + 1;\\
y_0 = 4p + 2;\\
z_0 = 3p - 7.
\end{cases}
Если учесть, что , а значит, выполн. равенство
M_0 \in \alpha
12x_0 + 4y_0 + 3z_0 - 4 = 0.
подставляя получим уравнение относительно
p
\Rightarrow 12(12p+1) + 4(4p+2) + 3(3p-7)- 4 = 0 \Rightarrow p =\frac{5}{169}.
Задача 2 (2)
\overline{AM_0} = \sqrt{(x_0 - 1)^2 + (y_0 - 2)^2 + (z_0 + 7)^2} =
\sqrt{(12p)^2 + (4p)^2 + (3p)^2} = 13|p|.
p =\frac{5}{169}
Т.к. и , то
\overline{AM_0} = 13|p|
\overline{AM_0} = 13\cdot \frac{5}{169} = \frac{5}{13}.
\rho(A; \alpha) = |\overline{AM_0}| = \frac{5}{13}.
Ответ:
M_0
A
\overline{n}
\alpha
или можно воспользоваться формулой...
\rho(Q; \alpha) = \frac{|AQ_x + BQ_y + CQ_z + D|}{\sqrt{A^2 + B^2 + C^2}},
M_0
Q
\overline{n}
\alpha
\alpha :: Ax + By + Cz + D = 0
где
A(1;2;-7)
Найти расстояние от точки до плоскости , заданной уравнением .
\alpha
12x + 4y + 3z - 4 = 0
\rho(A; \alpha) = \frac{|AA_x + BA_y + CA_z + D|}{\sqrt{A^2 + B^2 + C^2}}
=
\frac{|12\cdot 1 + 4\cdot 2 + 3\cdot(-7) + (-4)|}{\sqrt{12^2 + 4^2 + 3^2}}
= \frac{|-5|}{\sqrt{169}} = \frac{5}{13}.
\rho(A; \alpha) = \frac{5}{13}.
Ответ:
и тогда предыдущая задача решается так:
Задачи
AB = \sqrt{10}
4. В основании прямоугольного параллелепипеда лежит прямоугольник со сторонами , . Высота параллелепипеда . Найти расстояние от точки до плоскости
5. В кубе с ребром 2 точка — середина ребра . Найти расстояние от точки до плоскости . (Решить двумя способами)
AD = 3\sqrt{10}
AA_1 = \frac{6}{\sqrt{5}}
ABCDA_1B_1C_1D_1
ABCD
A
A_1DB.
ABCDA_1B_1C_1D_1
M
A_1D_1
C
AB_1M
1. В единичном кубе найти расстояние от точки до плоскости
A...D_1
B
ACD_1.
2. В правильной шестиугольной призме , все ребра которой равны , найти расстояние от точки до плоскости
A...F_1
B
ACB_1.
1
3. В правильной треугольной призме , все ребра которой равны , найти расстояние от точки до плоскости
A...С_1
A
A_1B_1C.
1
Угол между плоскостями
\varphi
\overline{n_1}
\overline{n_2}
\cos \varphi = \frac{|\overline{n_1} \cdot \overline{n_2}|}{|\overline{n_1}|\cdot | \overline{n_2}|}
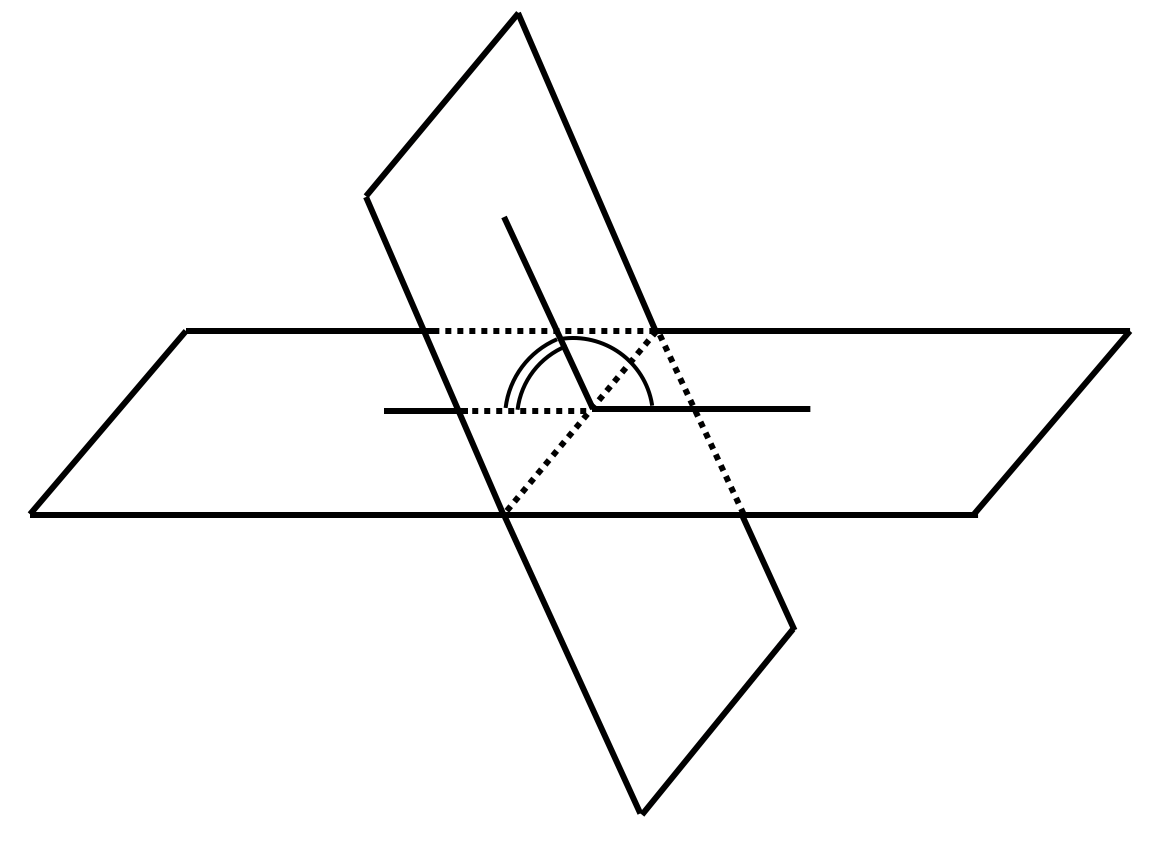
* Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла. Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
Задачи
2. В кубе точки и — середины ребер и соответственно . Найти угол между плоскостями и .
ABCDA_1B_1C_1D_1
E
F
AEF
BDD_1
A_1B_1
A_1D_1
1. В единичном кубе найти угол между плоскостями и .
A...D_1
AB_1D_1
BA_1C_1
Угол между прямой и плоскостью
\overline{n}
m
\overline{a}
\alpha
\varphi
\theta
\sin \varphi = \displaystyle{\frac{|\overline{n} \cdot \overline{a}|}{|\overline{n}|\cdot | \overline{a}|}} = \Bigl|\cos\bigl(\angle(\overline{a}; \overline{n})\bigr)\Bigr|
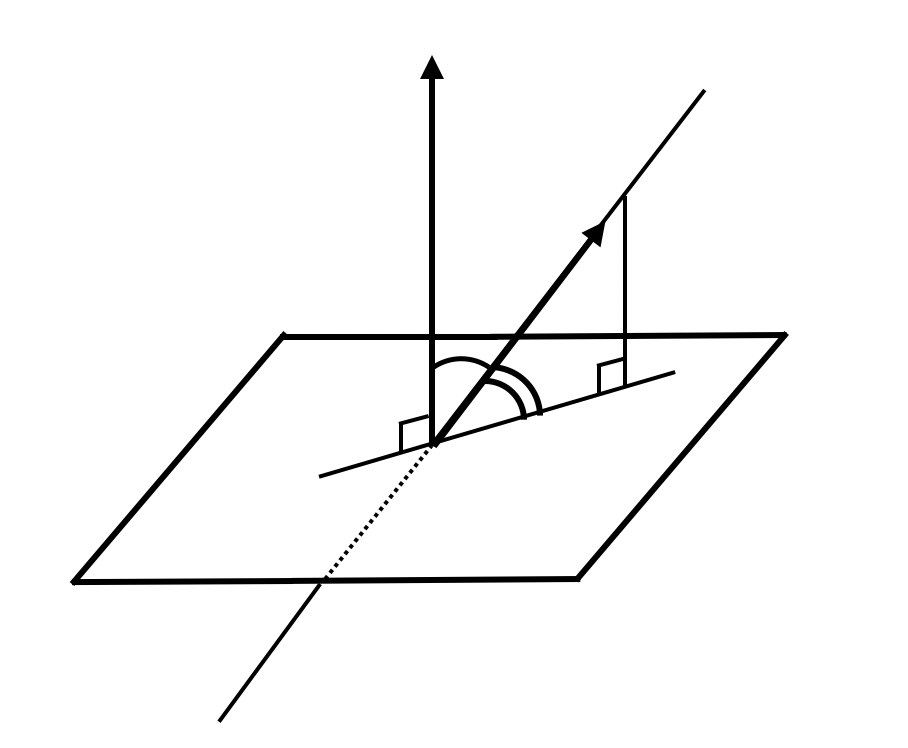
Задачи
1. В кубе точка — середина ребра . Найти синус угла между прямой и плоскостью .
ABCDA_1B_1C_1D_1
E
A_1B_1
AE
BDD_1
2. В кубе все рёбра равны 4. На его ребре отмечена точка так, что . Через точки и построена плоскость , параллельная прямой . , где — точка пересечения плоскости с ребром . Найти угол наклона плоскости к плоскости грани .
ABCDA_1B_1C_1D_1
BB_1
K
KB=3
K
C_1
\alpha
BD_1
A_1P : PB_1 = 2 : 1
P
\alpha
A_1B_1
\alpha
BB_1C_1C
Расстояние между скрещивающимися прямыми
a \parallel \alpha, b \subset \alpha, P \in a \Rightarrow
\rho(a; b) = \rho(P; \alpha) = \displaystyle{\frac{|AP_x + BP_y + CP_z + D|}{\sqrt{A^2 + B^2 + C^2}}},
Способ I. Ищем расстояние между одной из этих прямых и плоскостью, проходящей через вторую прямую параллельно первой.
\alpha :: Ax + By + Cz + D = 0.
где
a
b
\rho(a; b)
\begin{cases}
\\
\\
\\
\end{cases}
P
\alpha
P'
Способ II. Поиск расстояния между параллельными плоскостями, в которых находятся скрещивающиеся прямые.
=\rho(\alpha; \beta) = \displaystyle{\frac{|D_\alpha - D_\beta|}{\sqrt{A^2 + B^2 + C^2}}},
\alpha :: Ax + By + Cz + D_\alpha = 0,
где
\beta :: Ax + By + Cz + D_\beta = 0.
Расстояние между скрещивающимися прямыми (2)
a
b
\alpha
\beta
\begin{cases}
\\
\\
\\
\end{cases}
M_1
\rho(a; b)
M_2
\alpha \parallel \beta
\begin{cases}
\\
\\
\\
\end{cases}
\rho(a; b) =
\Leftarrow
a \in \alpha, b \subset \beta
a ∸ b
Способ III. Поиск расстояния между проекциями этих прямых на плоскость, которая перпендикулярна одной из этих прямых.
Расстояние между скрещивающимися прямыми (3)
a
b
\begin{cases}
\\
\\
\end{cases}
\rho(a; b)
b \perp \alpha
\alpha
a
— наклонная к
\alpha
M
Q
H
P
T
PH
— проекция на
a
\alpha
MH \perp \alpha, M \in \alpha
\begin{cases}
\\
\\
\\
\end{cases}
\rho(a; b) = \rho(PH; T) .
\Leftarrow
проекция перпендикулярной к плоскости прямой на на эту плоскость — точка
... но тут уже проще решить классическим способом.
Задачи (решить методом координат)
1. Дана правильная треугольная призма , ребра которой равны 2. Точка — середина ребра .
а) Доказать, что прямые и перпендикулярны.
б) Найти расстояние между прямыми и .
2. В кубе все рёбра равны 4. На его ребре отмечена точка так, что . Через точки и построена плоскость , параллельная прямой .
, где — точка пересечения плоскости с ребром .
Найдите угол наклона плоскости к плоскости грани .
3. В правильной шестиугольной призме
а) Докажите, что прямые и перпендикулярны.
б) Найдите расстояние между прямыми и .
ABCDEA_1B_1C_1D_1E_1
CE
BG
G
AD
AD
BG
ABCDA_1B_1C_1D_1
BB_1
K
KB=3
K
C_1
\alpha
BD_1
A_1P : PB_1 = 2 : 1
P
BB_1C_1C
ABCDEA_1B_1C_1D_1E_1
AB = 2, AA_1 = 3.
AC_1
BE
AC_1
BE
\alpha
\alpha
A_1B_1
Г1. Векторы
By vkrysanov320
