Элементарные функции. Элементарные преобразования графиков
11 класс
vkrysanov320@gmail.com
version 3.1, 26-08-2025; not fixed«Математический анализ не менее всеобъемлющ, чем сама природа: он определяет все ощутимые взаимосвязи, измеряет времена, пространства, силы, температуры.»
Жан-Батист Жозеф Фурье

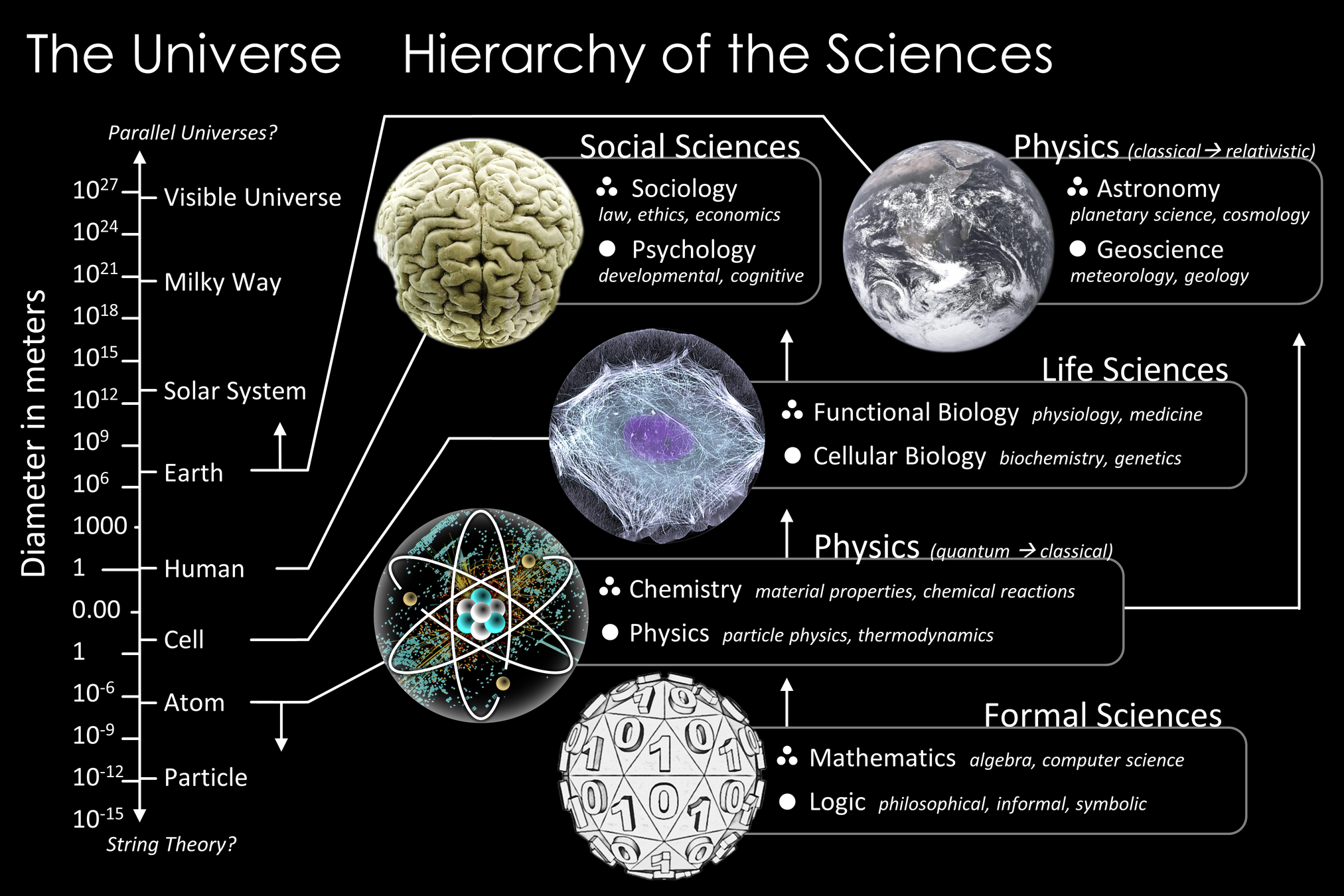
Maтематика в системе наук

Что изучает матанализ?

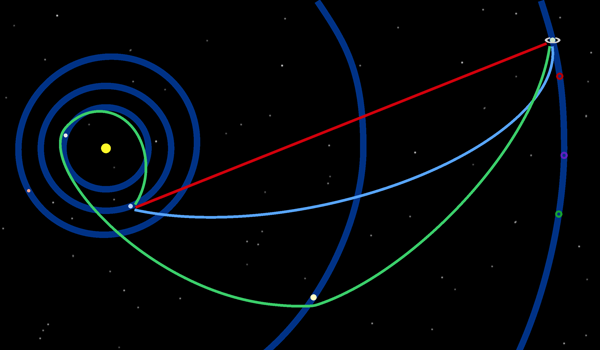
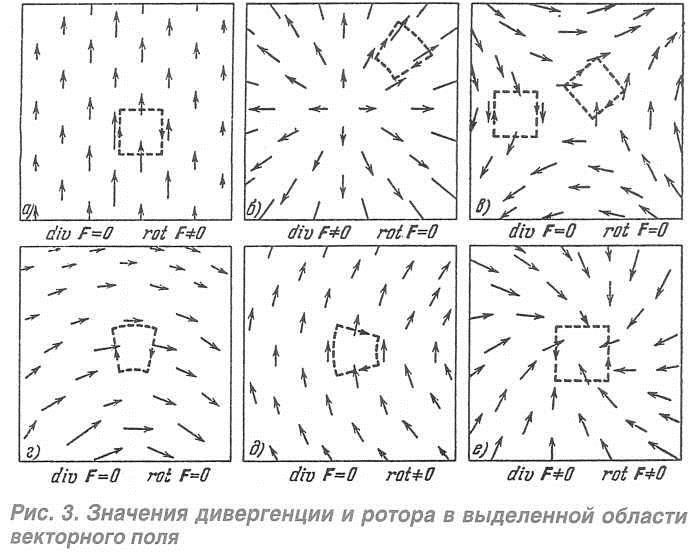
Интегральное исчисление
Дифференциальное исчисление
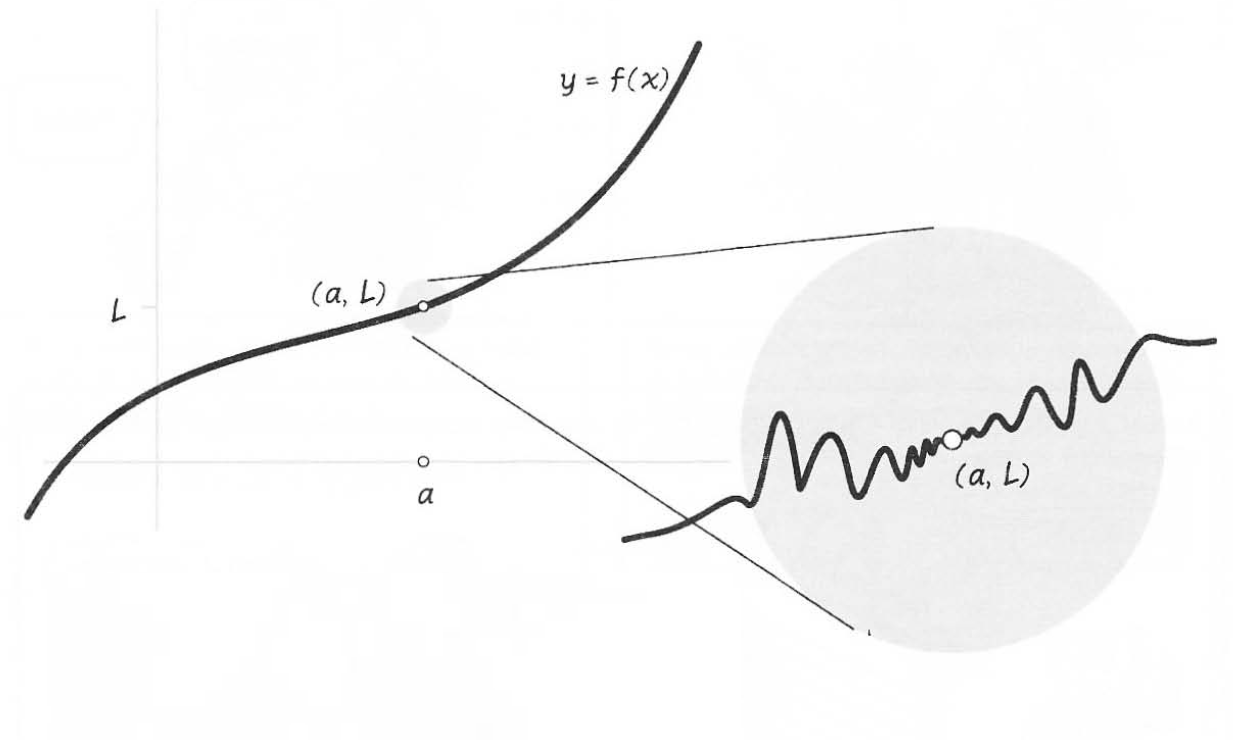
Теория пределов
Математический анализ — совокупность разделов математики, соответствующих историческому разделу под наименованием «анализ бесконечно малых», объединяет дифференциальное и интегральное исчисления.
Движение, переменные величины и их взаимосвязи окружают нас повсюду. Различные виды движения и их закономерности составляют основной объект изучения конкретных наук: физики, геологии, биологии, социологии и др. Поэтому точный язык и соответствующие математические методы описания и изучения переменных величин оказались необходимыми во всех областях знания примерно в той же степени, в какой числа и арифметика необходимы при описании количественных соотношений.
Что изучает матанализ? (2)
Так вот, математический анализ и составляет основу языка и математических методов описания переменных величин и их взаимосвязей.
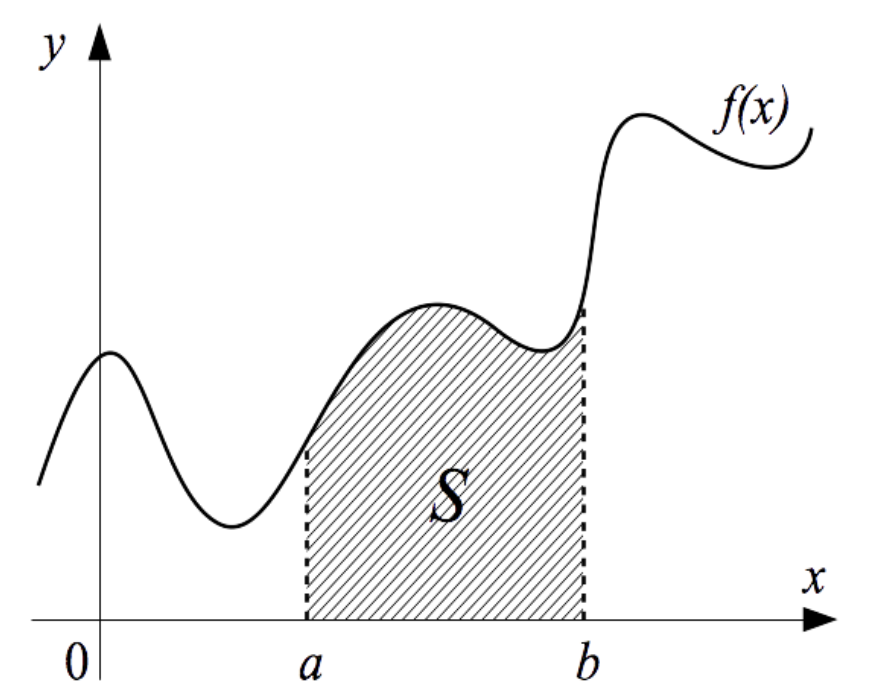
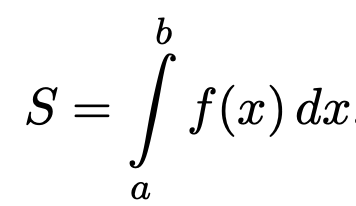
Понятие числовой функции
Числовой (вещественной) функцией называется соответствие между элементами двух числовых множеств и , в котором каждому элементу из множества соответствует один элемент из .
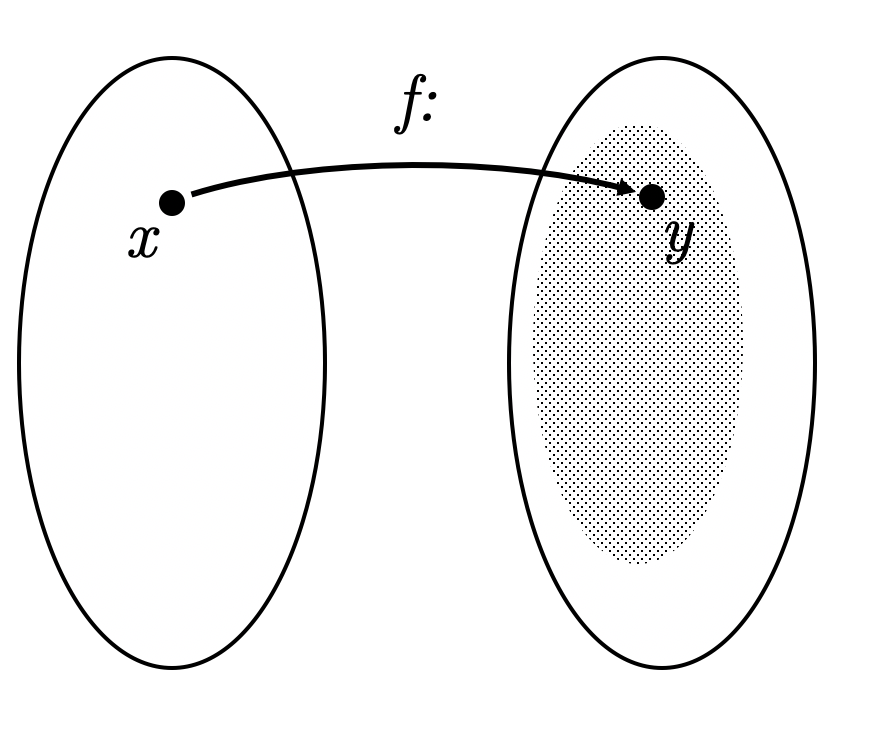
(заштрихованная часть)
Обозначение:
где обозначает закон, определяющий соответствие
— независимая переменная (аргумент)
— зависимая переменная (функция)
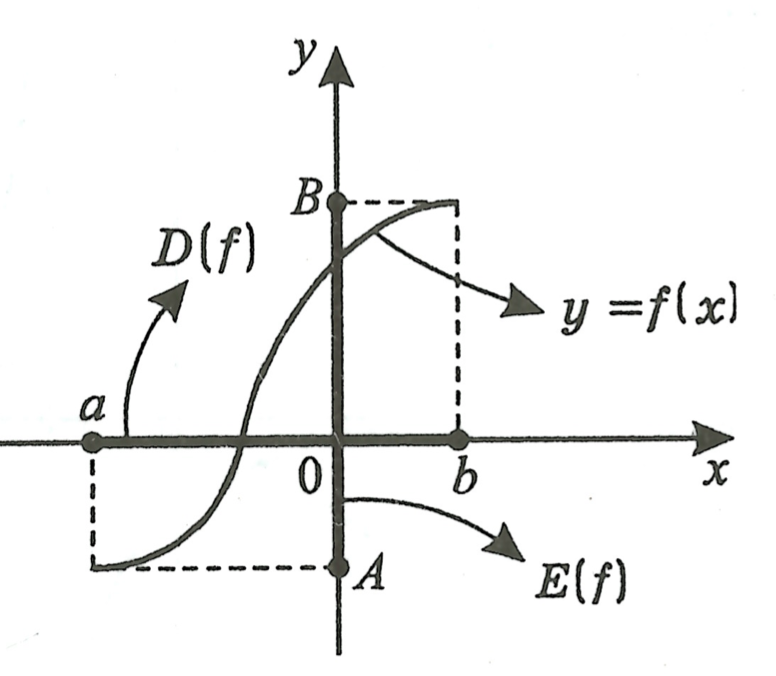
Способы задания функции
(1) Табличный способ задания функции
При табличном способе функция задается таблицей ряда значений аргумента и соответствующих значений функции.
Способы задания функции (2)
При аналитическом способе функция посредством формул. При этом функция может быть задана в декартовых или полярных координатах, в явном, неявном виде или параметрическом виде.
(2) Аналитический способ задания функции
Функция в неявном виде
Уравнение вида на некотором числовом множестве , если для каждого существует единственное число , удовлетворяющему данному уравнению.
Пример:
Функция в явном виде
Если в уравнении , определяющем функцию, закон соответствия задается конкретным аналитическим выражением, зависящим от .
Пример:
А что можно сказать о
?
Способы задания функции (2.2)
При аналитическом способе функция посредством формул. При этом функция может быть задана в декартовых или полярных координатах, в явном, неявном виде или параметрическом виде.
(2) Аналитический способ задания функции
Функция в параметрическом виде
При параметрическом задании функции значение функции и ее аргумента задаются как функции от некоторой переменной из множества :
Если эти функции вычислить при одном и том же значении параметра , получим получим координаты на плоскости (когда параметр пробегает все значения из множества , тогда точка описывает некоторую линию в плоскости ).
Способы задания функции (3)
При графическом способе функция задается с помощью графика.
(3) Графический способ задания функции
Замечание: Множество точек на координатной плоскости является графиком некоторой функции только в том случае, когда каждая параллельная оси прямая пересекает его не более чем в одной точке.
График числовой функции — это множество точек, на плоскости с координатами .
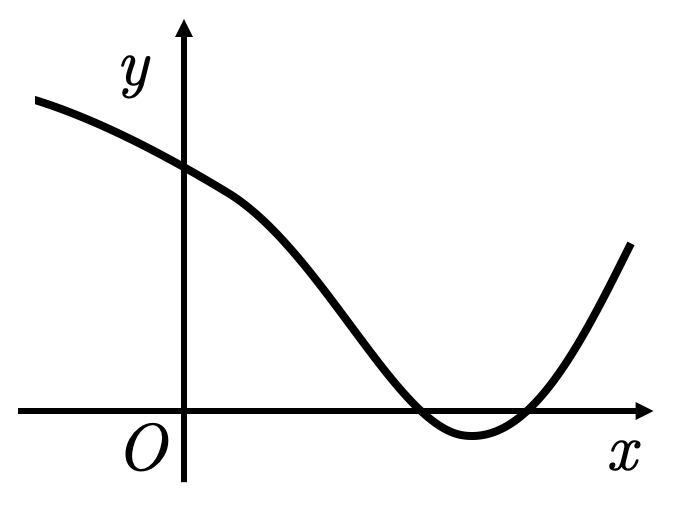
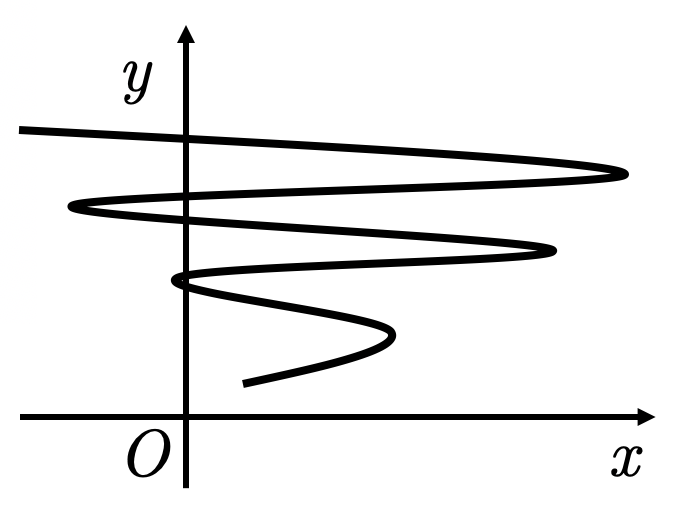
График функции
Не является графиком функции
*График функции иногда можно построить с помощью элементарных преобразований графика, некоторой уже известной функции.
Элементарные преобразования графиков функций
(1) Параллельный сдвиг вдоль осей координат
Параллельный сдвиг вдоль оси Oy
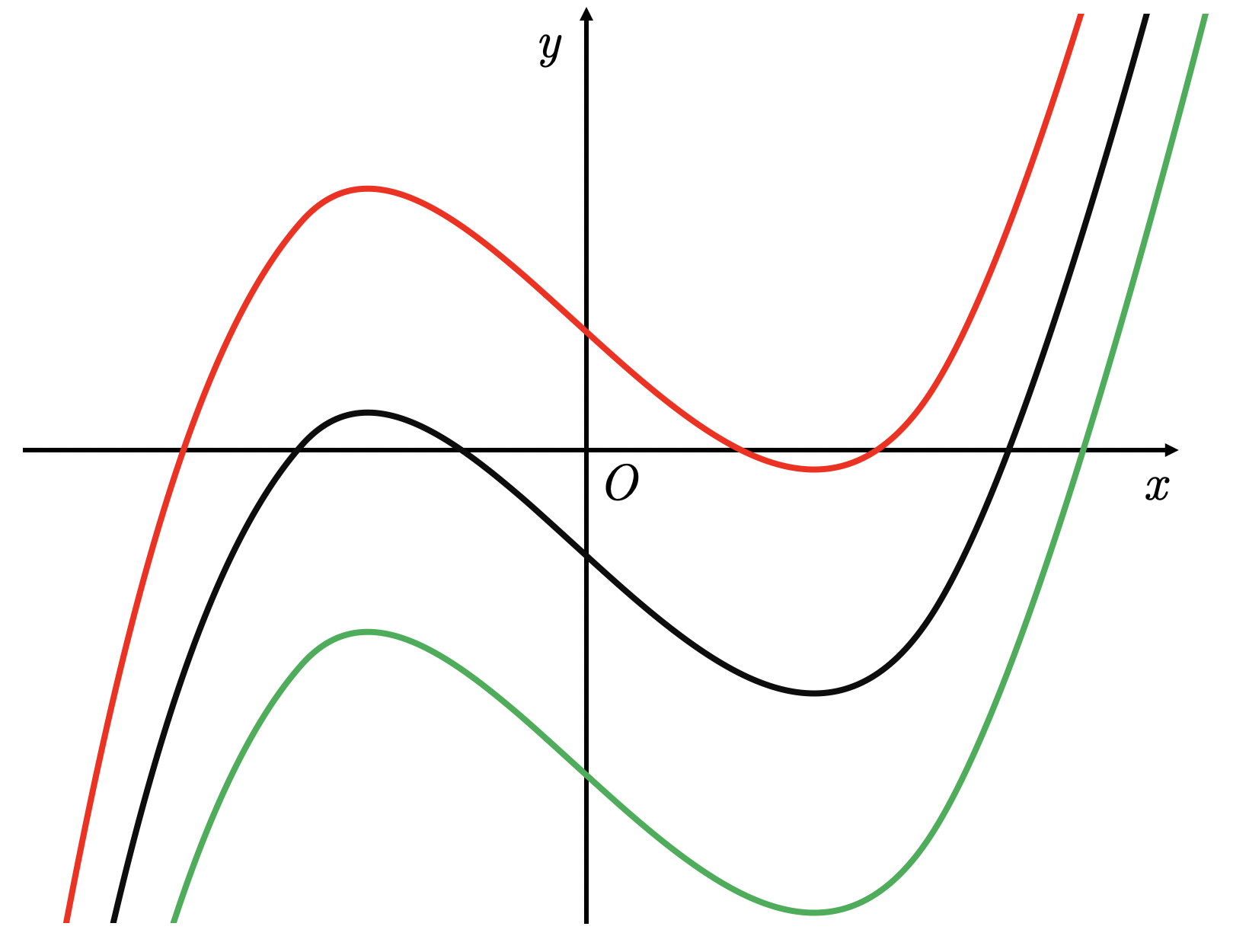
График функции
получается из графика
сдвигом вдоль оси
на
единиц:
- вверх, если
- вниз, если
Параллельный перенос вдоль Ox
вправо, если :
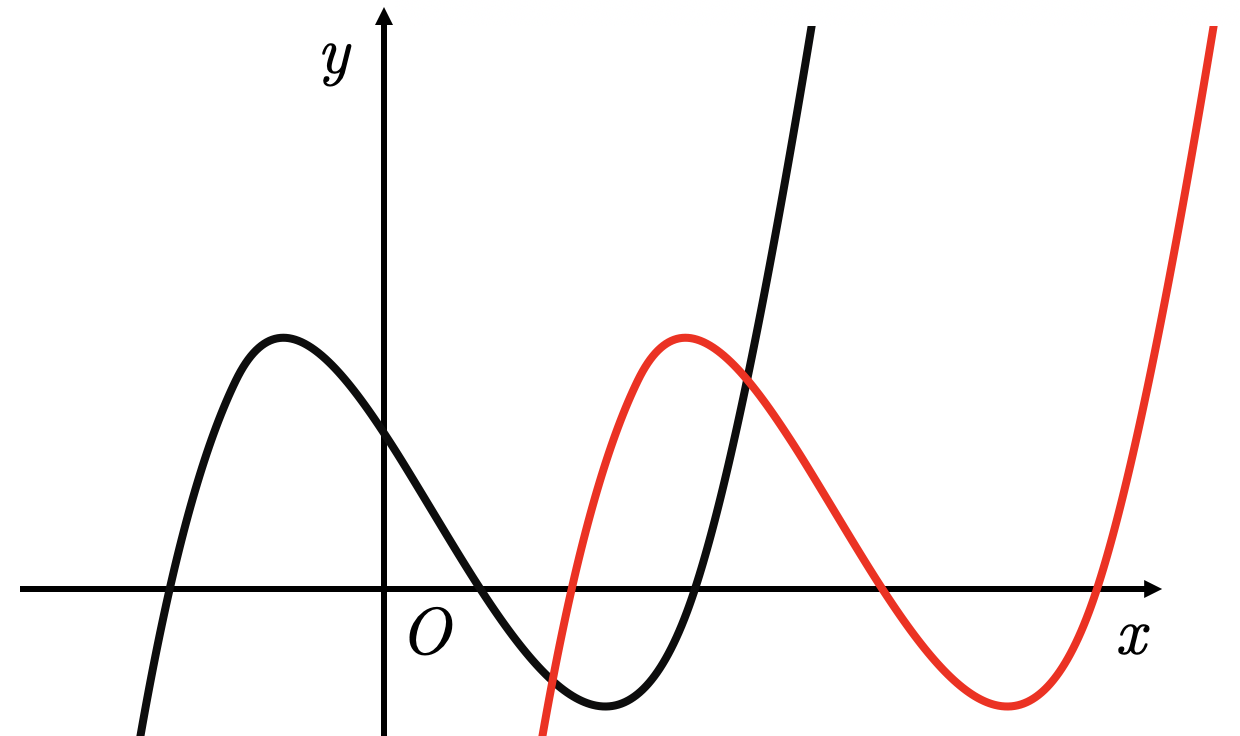

График функции
получается из графика
влево, если :
сдвигом вдоль оси
на
единиц:
(2) Растяжение (сжатие) вдоль осей координат
Растяжение (сжатие) вдоль оси Oy
График функции
получается из графика
растяжением (сжатием) вдоль оси
в:
- растяжением в раз, если
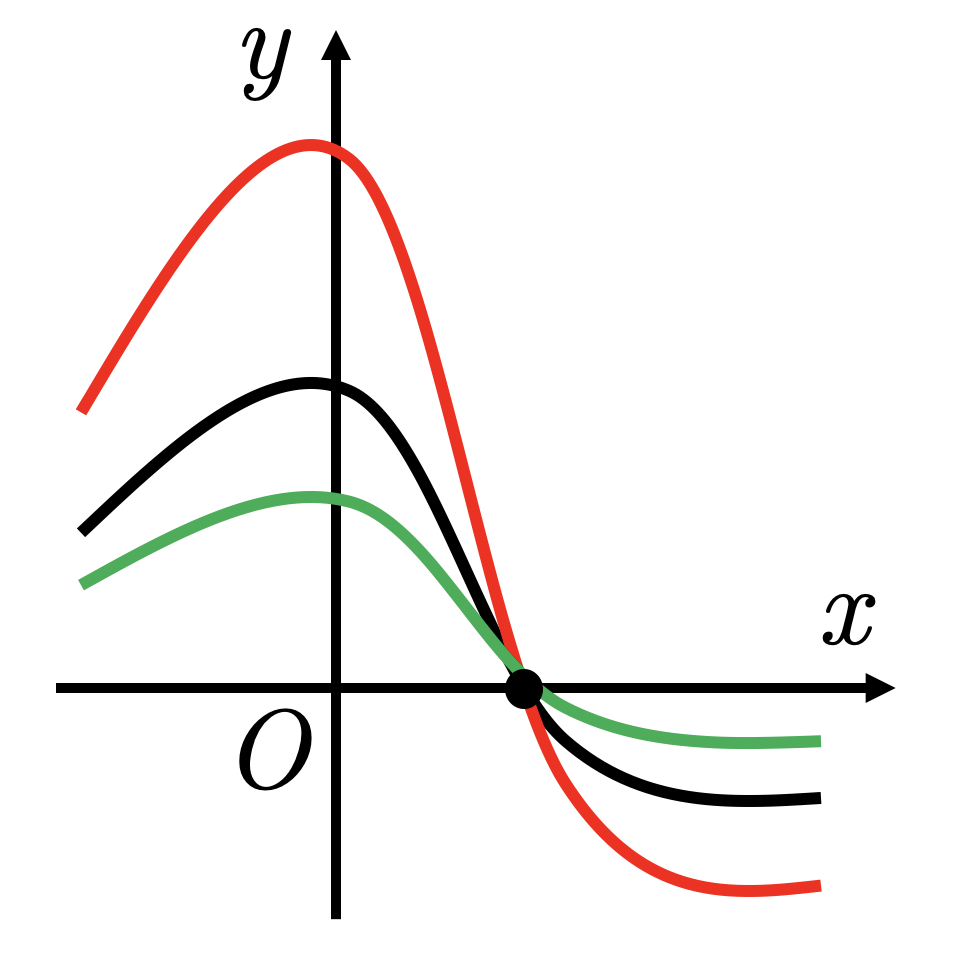
- сжатием в раз, если
Растяжение (сжатие) вдоль оси Ox
График функции
получается из графика
растяжением (сжатием) вдоль оси :
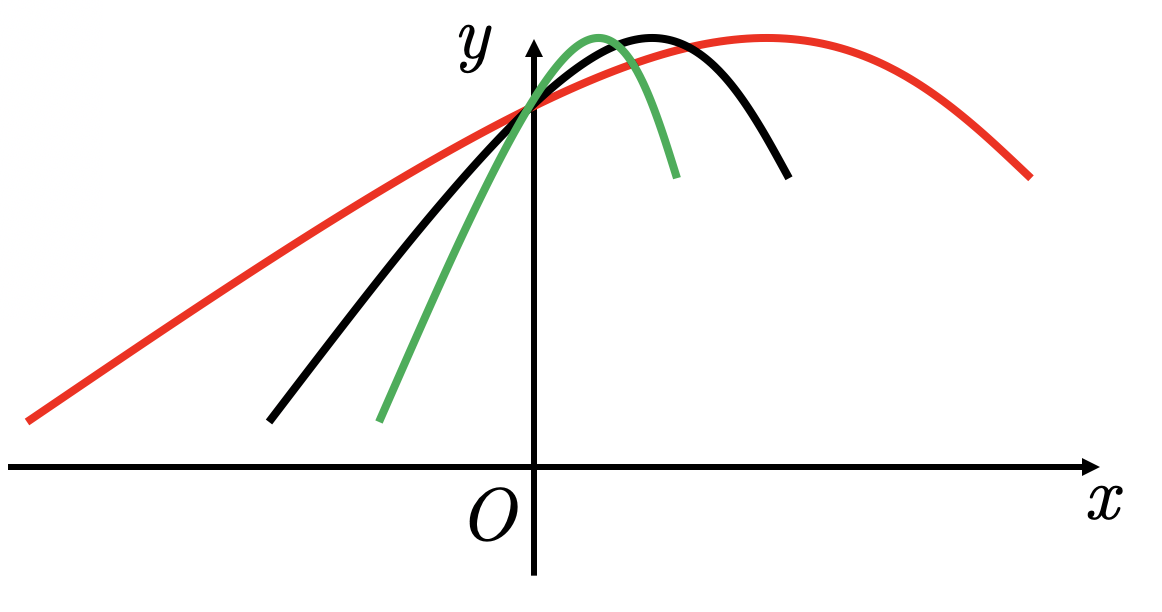
- сжатием в раз, если
- растягиванием в раз, если
(3) Симметричное отражение относительно осей координат
Симметричное отражение отн. Ox
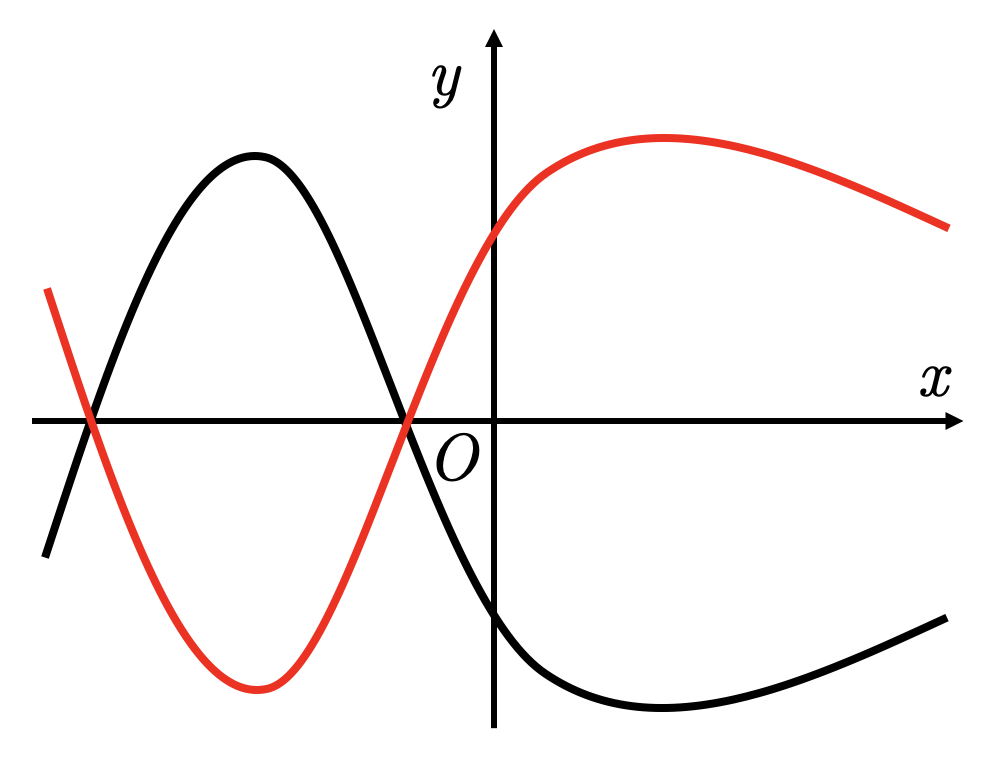
График функции
получается из графика
симметричным отражением относительно оси :
Симметричное отражение отн. Oy
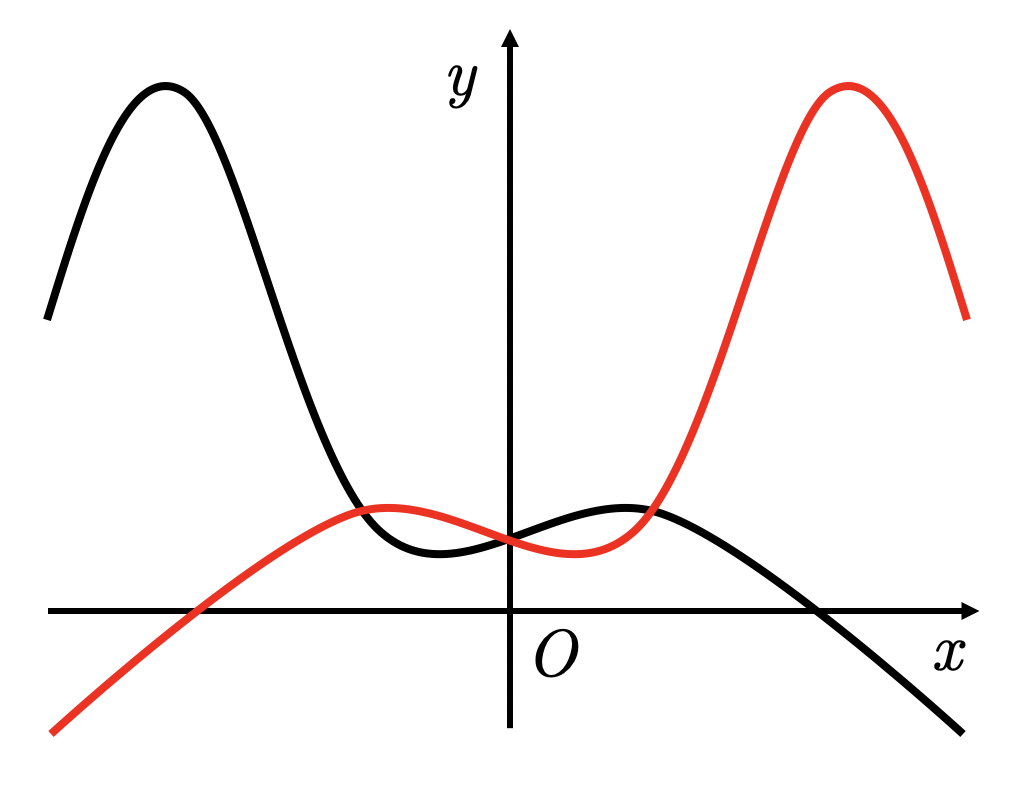
График функции
получается из графика
симметричным отражением относительно оси :
(4) Преобразования, связанные с модулем
Преобразования вида
График функции
получается из графика
следующим образом:
часть графика, расположенная ниже оси , симметрично отражается относительно этой оси, остальная его часть остается без изменения.
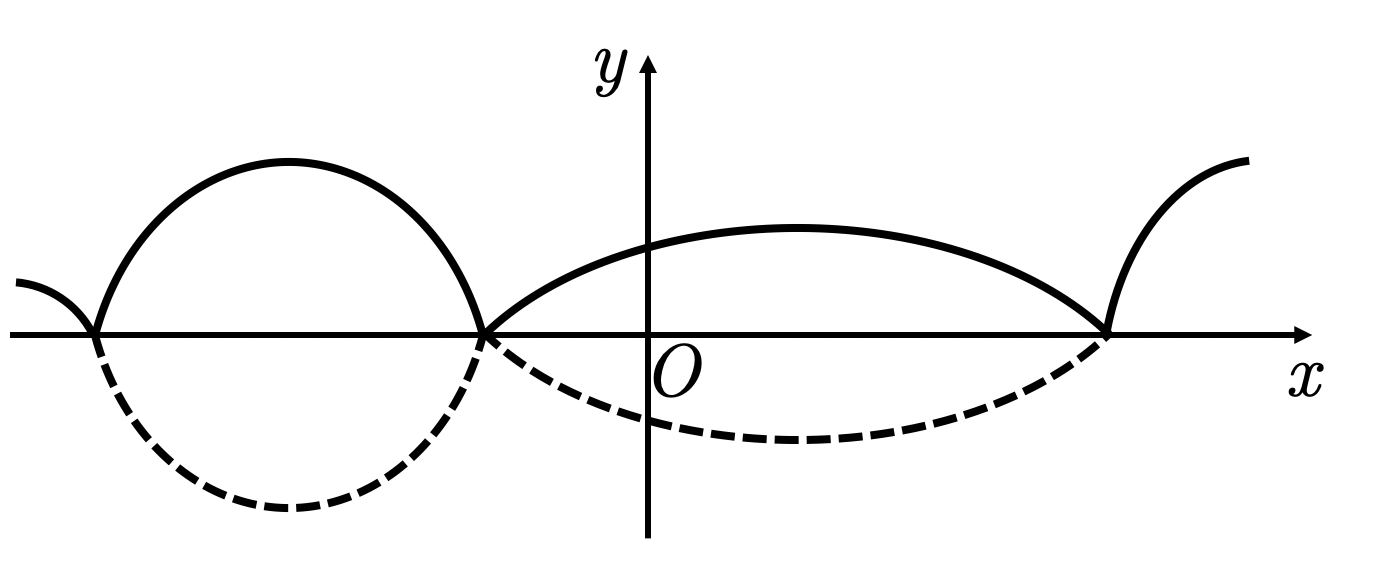
Преобразования вида
График функции
получается из графика
следующим образом:
часть графика, расположенная в области остается без изменений, а его часть в области удаляется и заменяется симметричным отображением относительно оси части графика области .
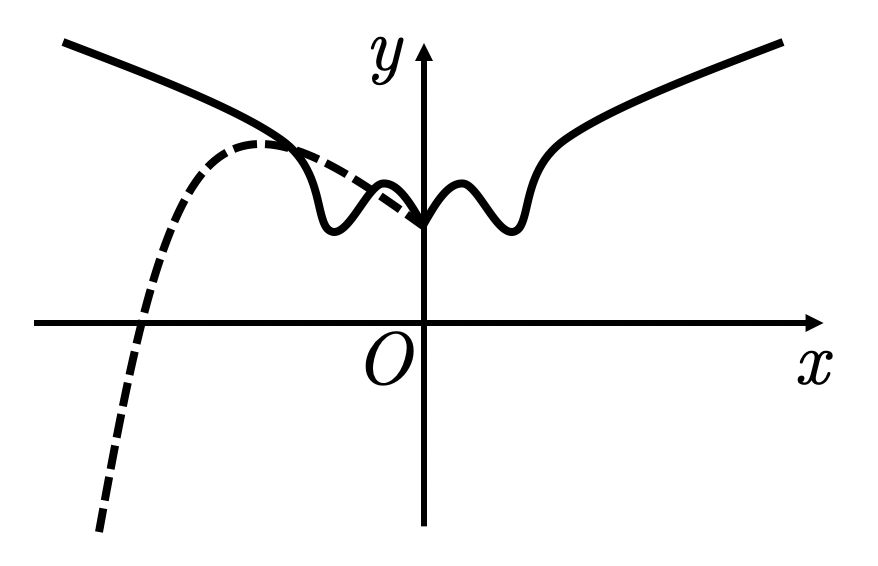
Арифметические операции над функциями
Арифметические операции над ф-ями
Пусть даны две функции и и области определения
и соответственно.
Определим новую функцию .
Тогда ОДЗ для каждой операции:
Композиция функций
Пусть область значений функции содержится в области значений функции :
Тогда функция называется сложной функцией или композицией и .
внешняя функция
внутренняя функция
Обозначение:
Свойства функции
Чётные и нечетные функции
Числовая функция называется чётной, если ее область определения симметрична относительно начала координат и для всех
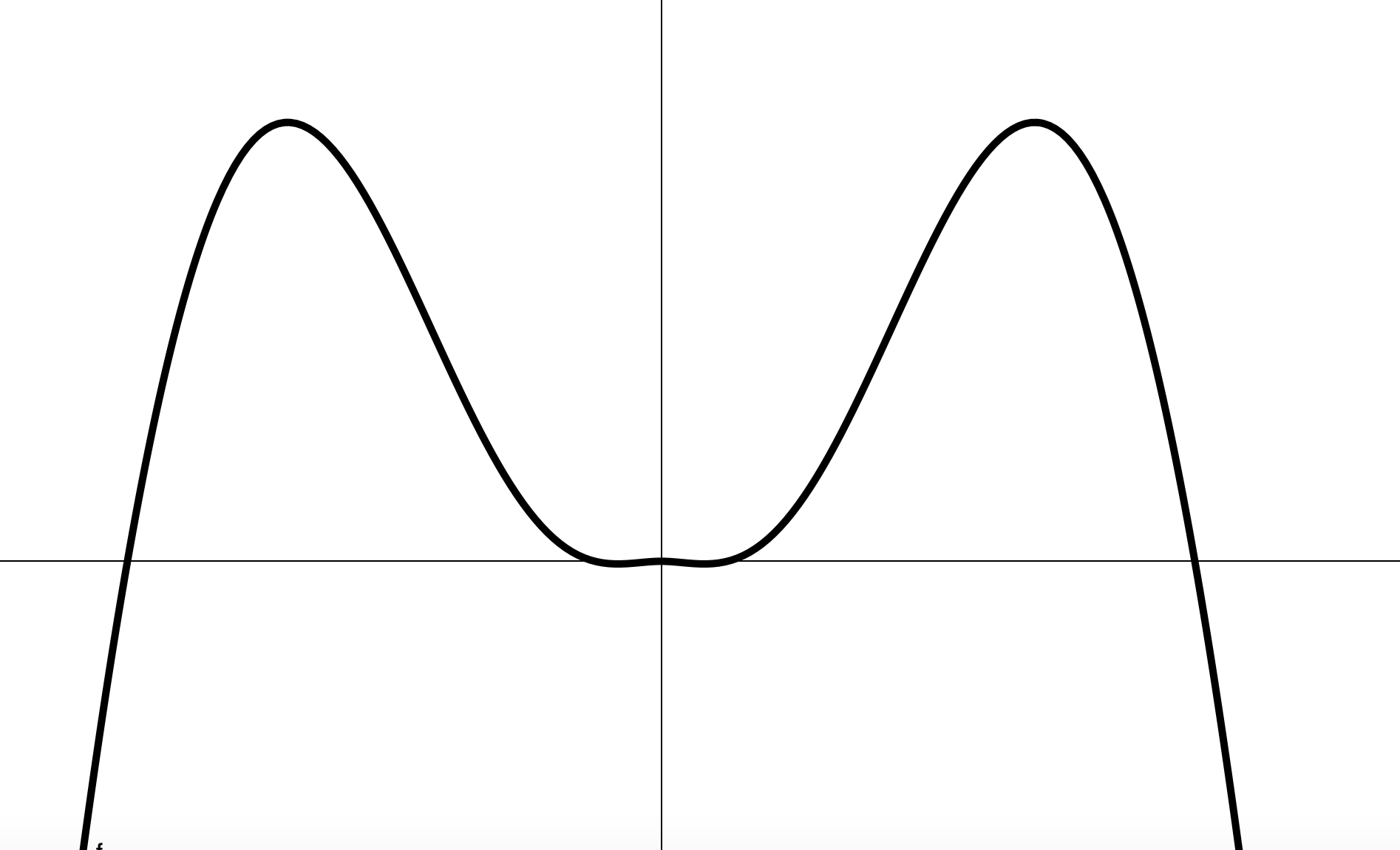
График четной функции
Числовая функция называется нечётной, если ее область определения симметрична относительно начала координат и для всех
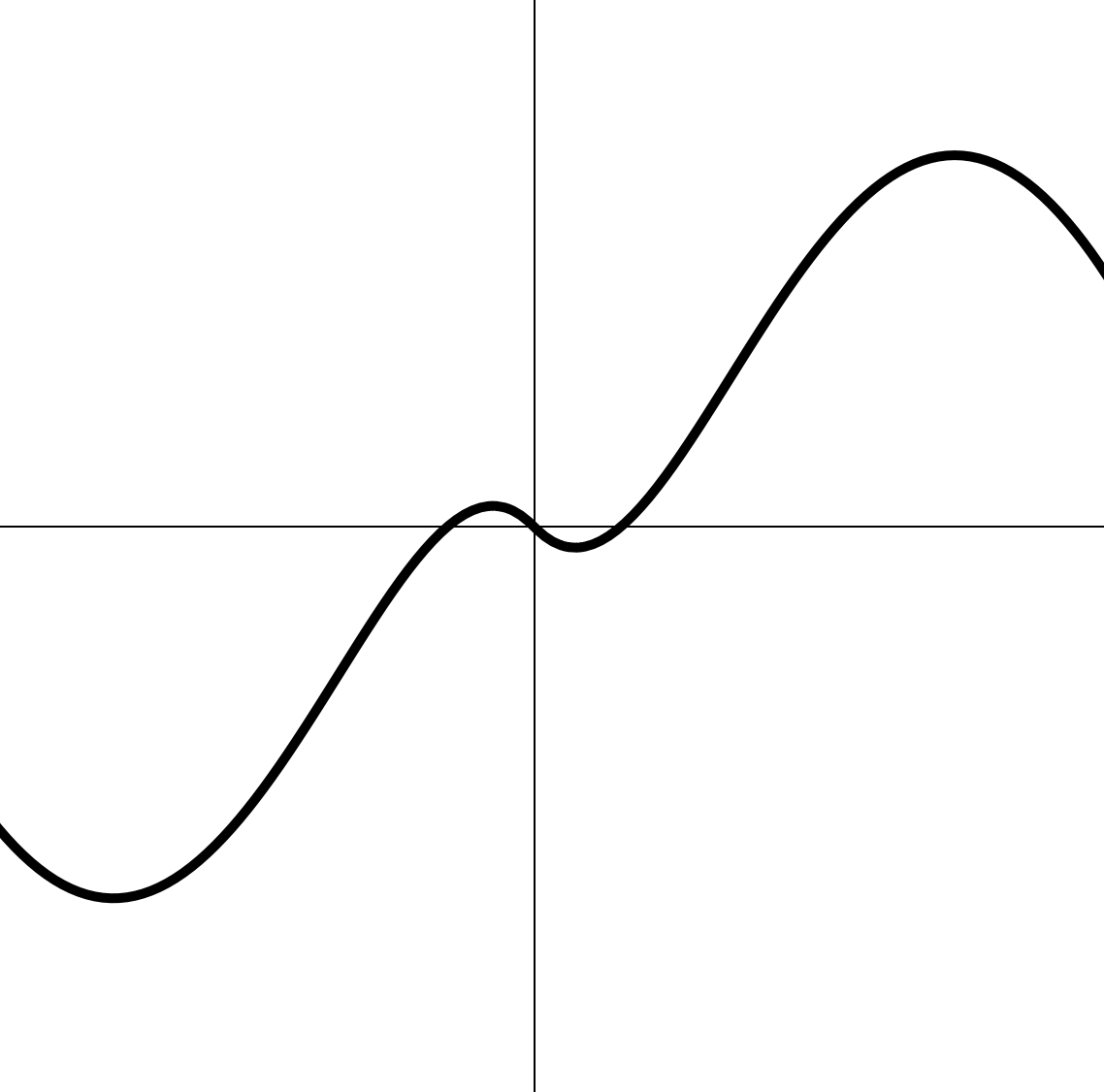
График нечетной функции
Если функция не является ни четно, ни нечетной, то такая ф-я называется функцией общего вида.
Периодичность функции
Функция называется периодической с периодом если,
и принадлежит области определения функции и
для любого .
- Все периоды кратны наименьшему :
- Сумма, разность, произведение и частное периодических функций с периодом является периодическая функция с периодом .
- Если ф-я периодическая с периодом , то ее график переходит сам в себя при сдвиге вдоль на единиц влево или вправо.

Периодичность функции (2)
Теорема: Если функция периодическая с периодом , то функция
будет так же периодической с периодом:
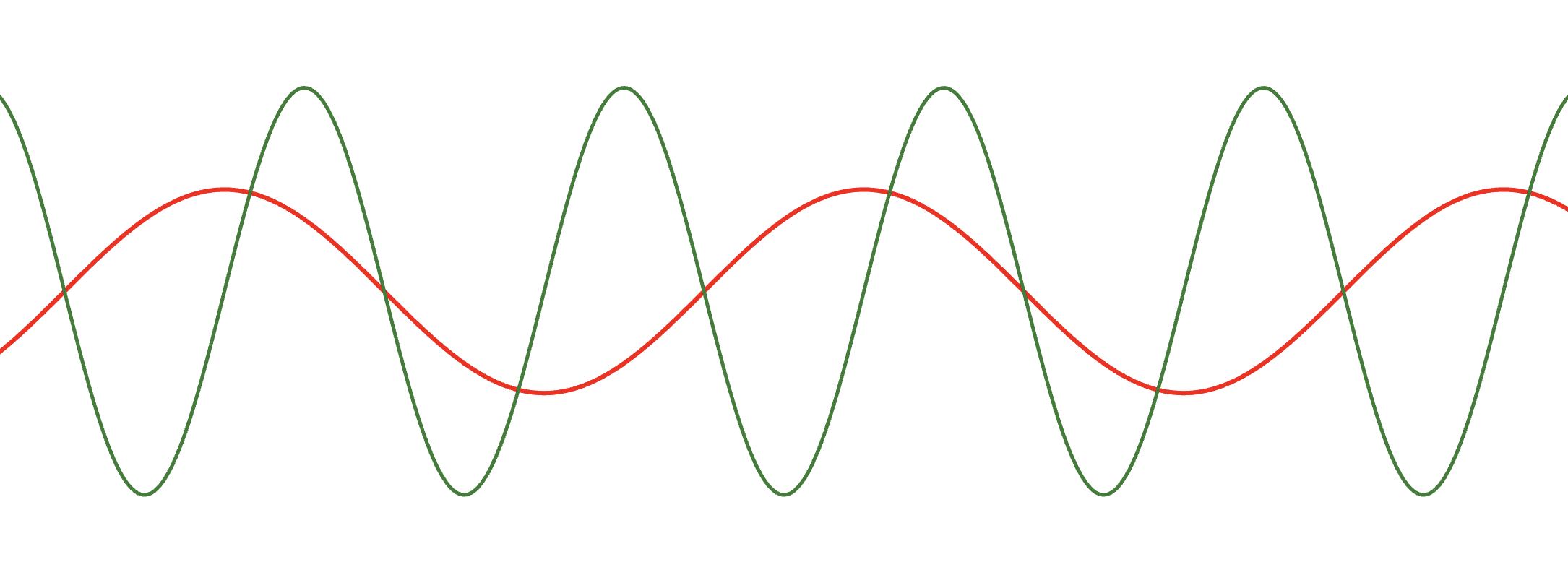
Ограниченность функции
Функция , определенная на множестве , называется ограниченной, если множество её значений ограниченно как сверху, так и снизу.
Функция , определенная на множестве , называется ограниченной сверху, если множество её значений ограниченно сверху. Иначе говоря, функция ограничена сверху, если существует такая постоянная , что для каждого выполняется неравенство
Функция , определенная на множестве , называется ограниченной снизу, если множество её значений ограниченно снизу. Иначе говоря, функция ограничена снизу, если существует такая постоянная , что для каждого выполняется неравенство
Ограниченность функции (2)
Монотонность функции
Функция называется возрастающей на множестве , если для любых из неравенства следует неравенство
Функция называется убывающей на множестве , если для любых из неравенства следует неравенство
строго!!!
Функция называется монотонной на множестве (области монотонности), если она является либо возрастающей, либо убывающей на этом множестве.
Монотонность функции (2)
Функция называется невозрастающей на множестве , если для любых из неравенства следует неравенство
Функция называется неубывающей на множестве , если для любых из неравенства следует неравенство


Максимумы минимумы функции
Точка называется точкой максимума/минимума функции на некотором множестве , если для всех выполняются неравенства:
для максимума:
для минимума:
Если указанное множество представляет собой некоторую окрестность точки , то в этом случае называют точкой локального максимума/минимума.
точки локального максимума или минимума называют точками экстремума.
— точка лок. максимума
— точка лок. минимума
Асимптота графика функции
Асимптотой называют прямую линию, если график функции неограниченно сближается с этой прямой при удалении точки графика в бесконечность.
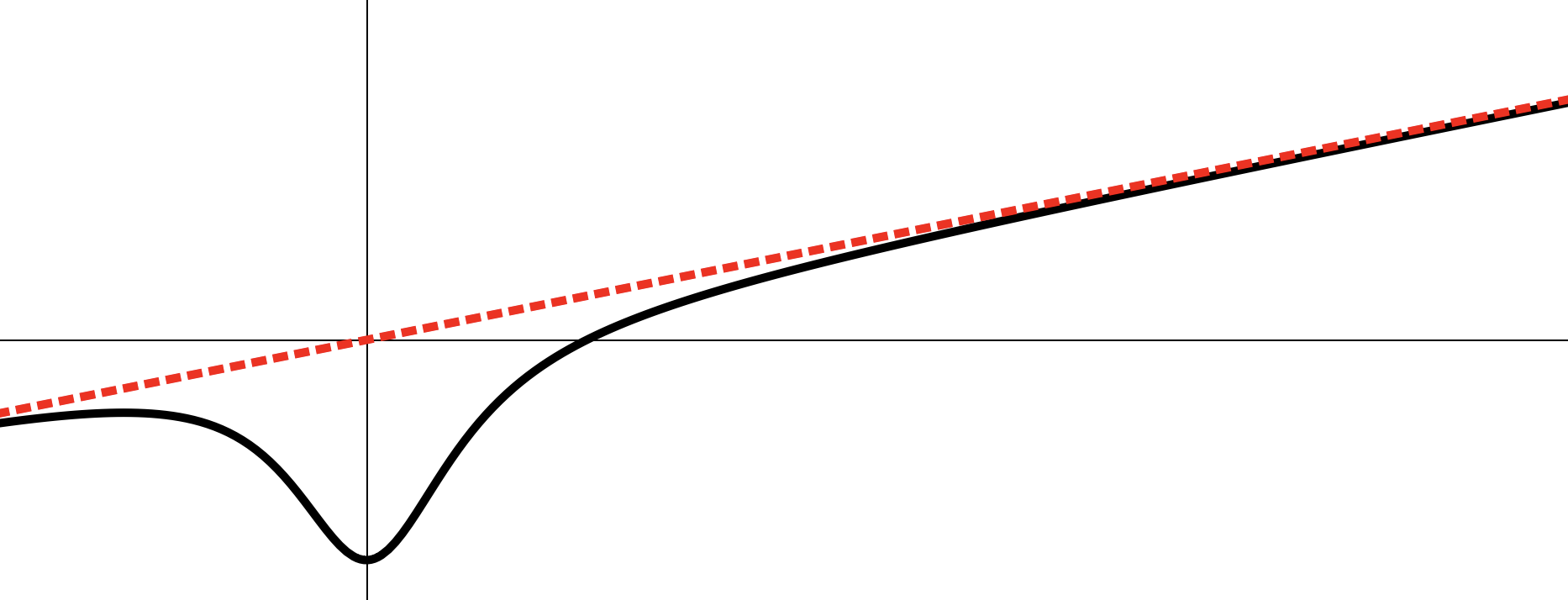
Обратимость ф-ии и понятие обратной ф-ии
Обратимая функция — это функция, которая принимает каждое своё значение в единственной точке области определения.
Две функции и являются взаимно обратными, если выполняются два условия:
Обратная функция может существовать только для обратимой функции.
для всех в области определения ;
для всех в области определения .
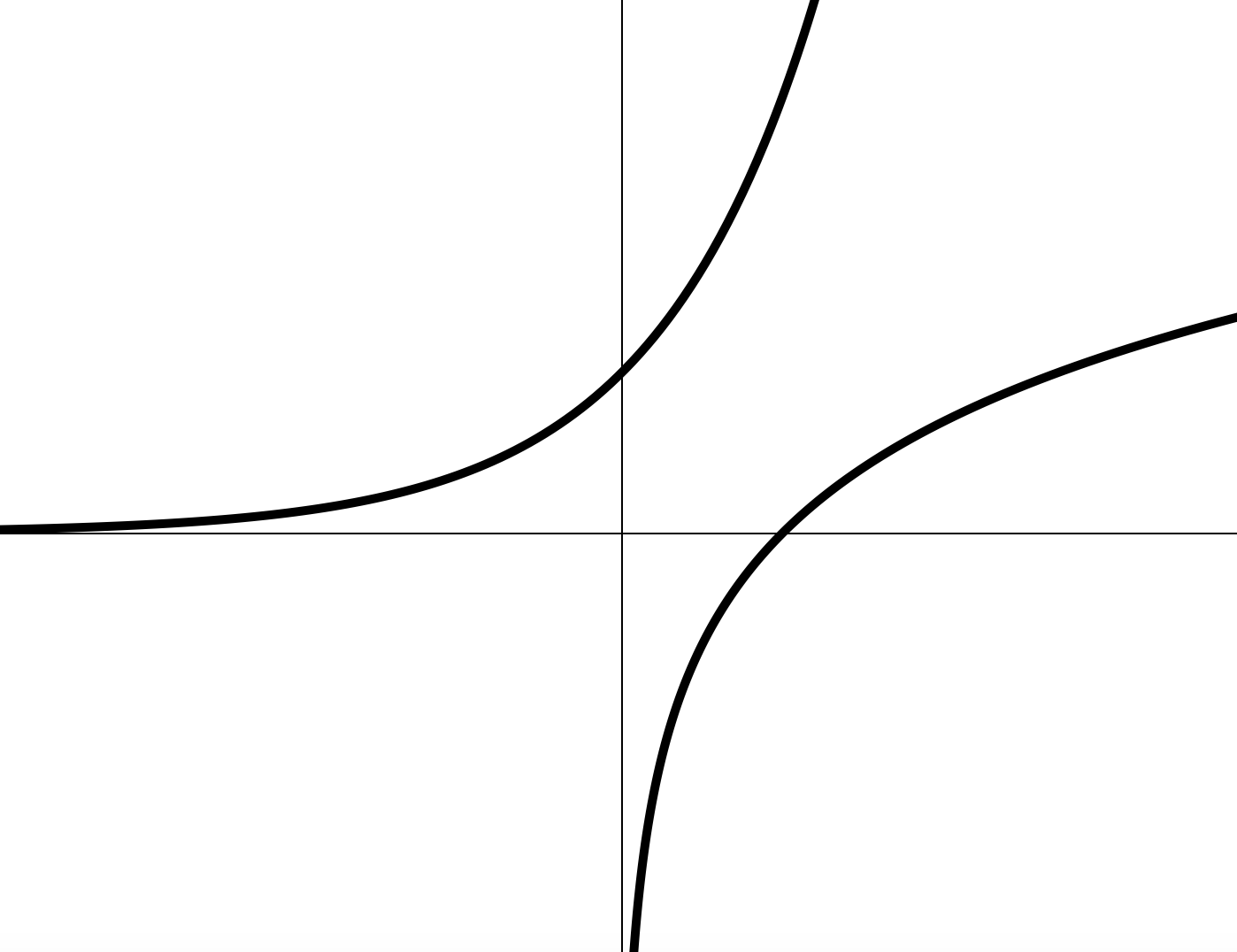
1) График взаимно обратных функций симметричен относительно прямой
2)
3) Если — возрастающая/убывающая функция, то она имеет обратную функцию, которая также является возрастающей/убывающей.
обозначение взаимно обратной ф-ии
Типы отображений
Инъективное отображение (инъекция)
Отображение называется инъективным, если для любых из неравенства следует неравенство .
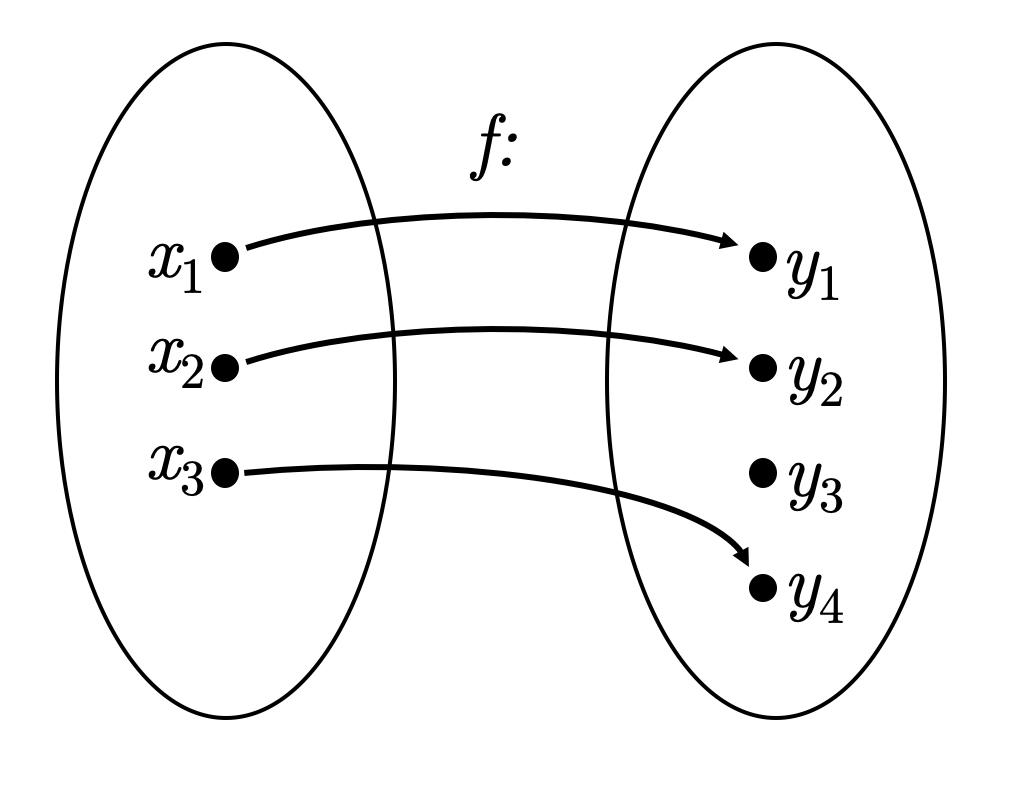
Примеры:
— отображение инъективно.
— отоб-е не инъективно.
Контрпример:
Сюръективное отображение (сюръекция)
Отображение называется сюръективным, если для всех существует такой, что .
Примеры:
— отображение сюръективно.
— отоб-е не сюръективно.
Контрпример: не найдется такого , что
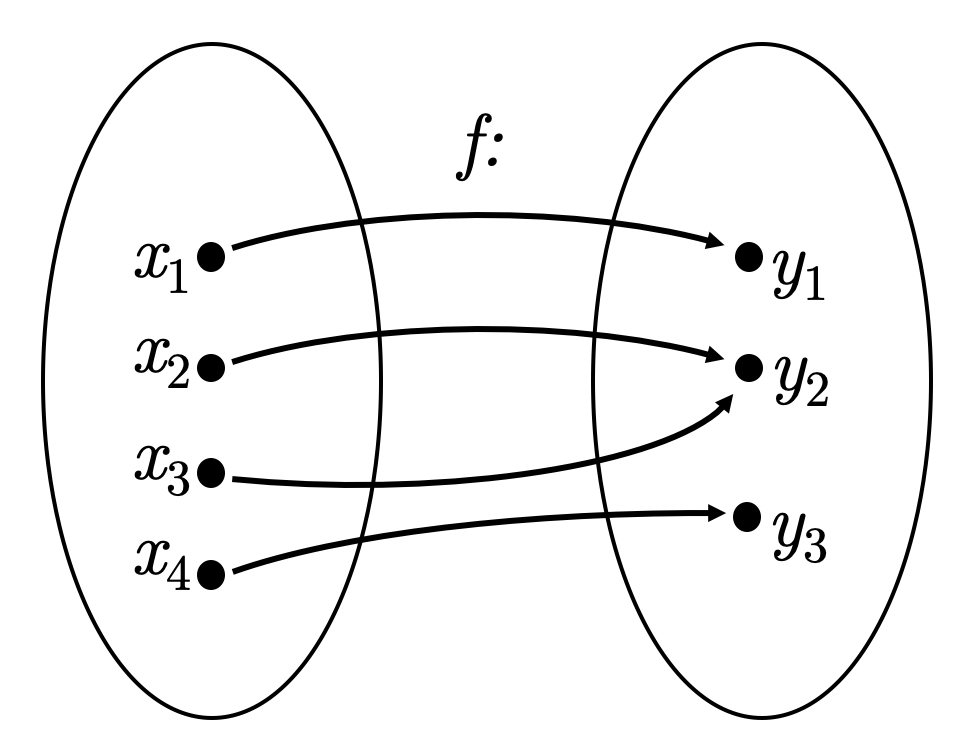
Биективное отображение (биекция)
Отображение называется биектиыным, если оно сюръективно и инъективно одновременно.
Примеры:
— отображение биективно.

— отображение биективно.
Элементарные функции и их свойства
I. Степенная функция
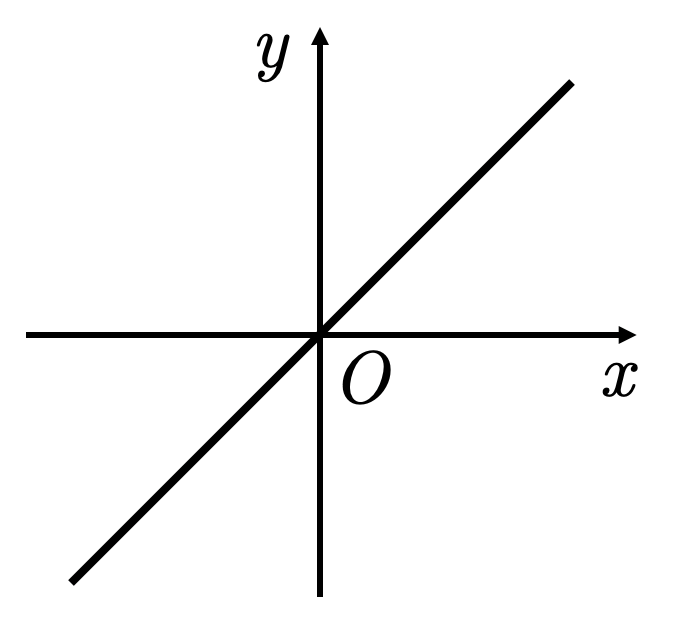
1. Линейная функция
- ;
- ;
- точка пересечения с осями координат: ;
- неограниченная;
- непериодическая;
- нечетная (график симметричен относительно начала координат);
- возрастающая;
- обратимая (функция обратна сама себе);
- графиком функции является прямая.
I. Степенная функция (2)
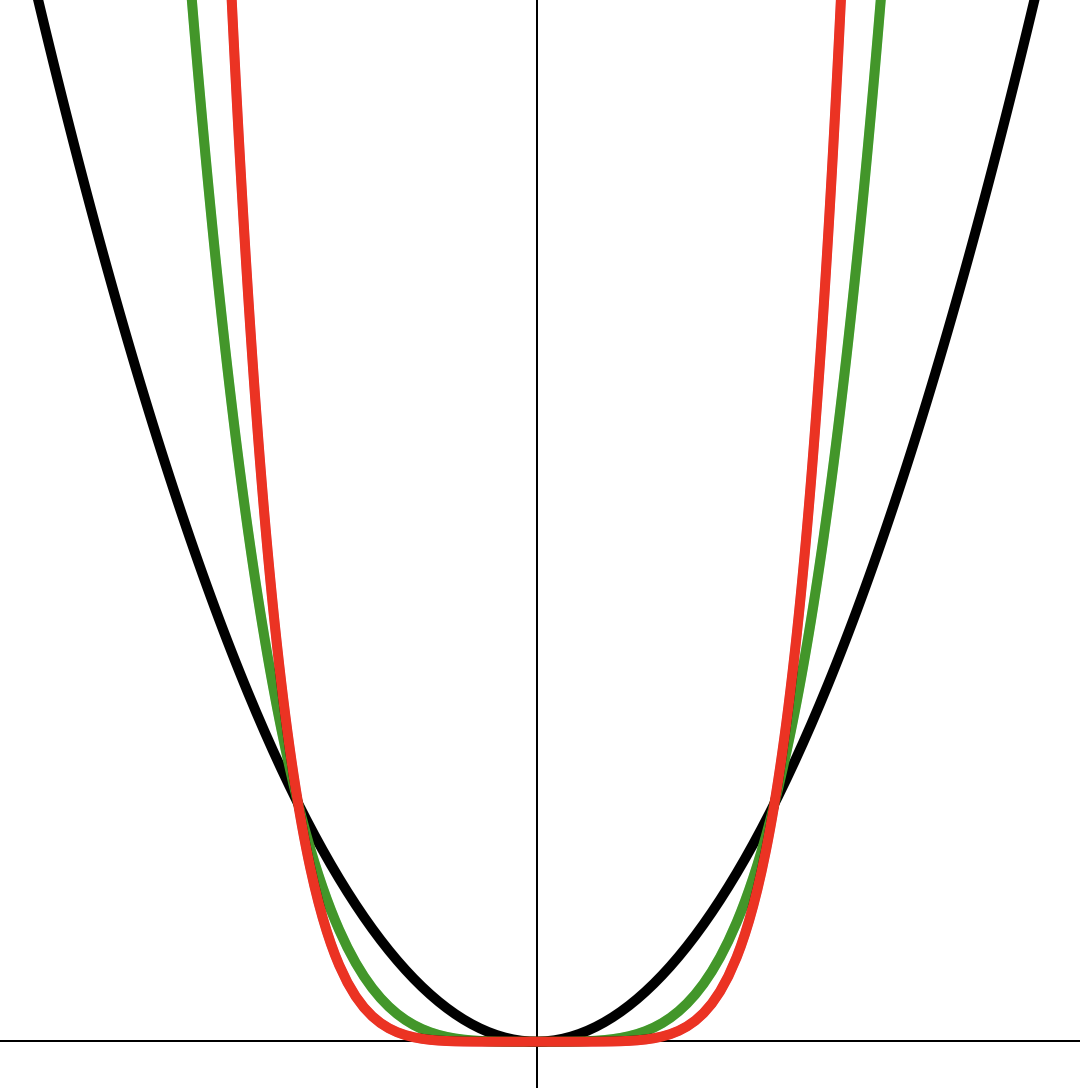
2. Функция вида
- ;
- ;
- точка пересечения с осью : ;
- ограниченна снизу числом ;
- непериодическая;
- четная;
- функция убывает на ;
- функция возрастает на ;
- функция необратимая.
— четное
I. Степенная функция (3)
Функция вида
- точек пересечения с осями нет
- неограниченная
- непериодическая
- четная
- асимптоты графика — оси координат
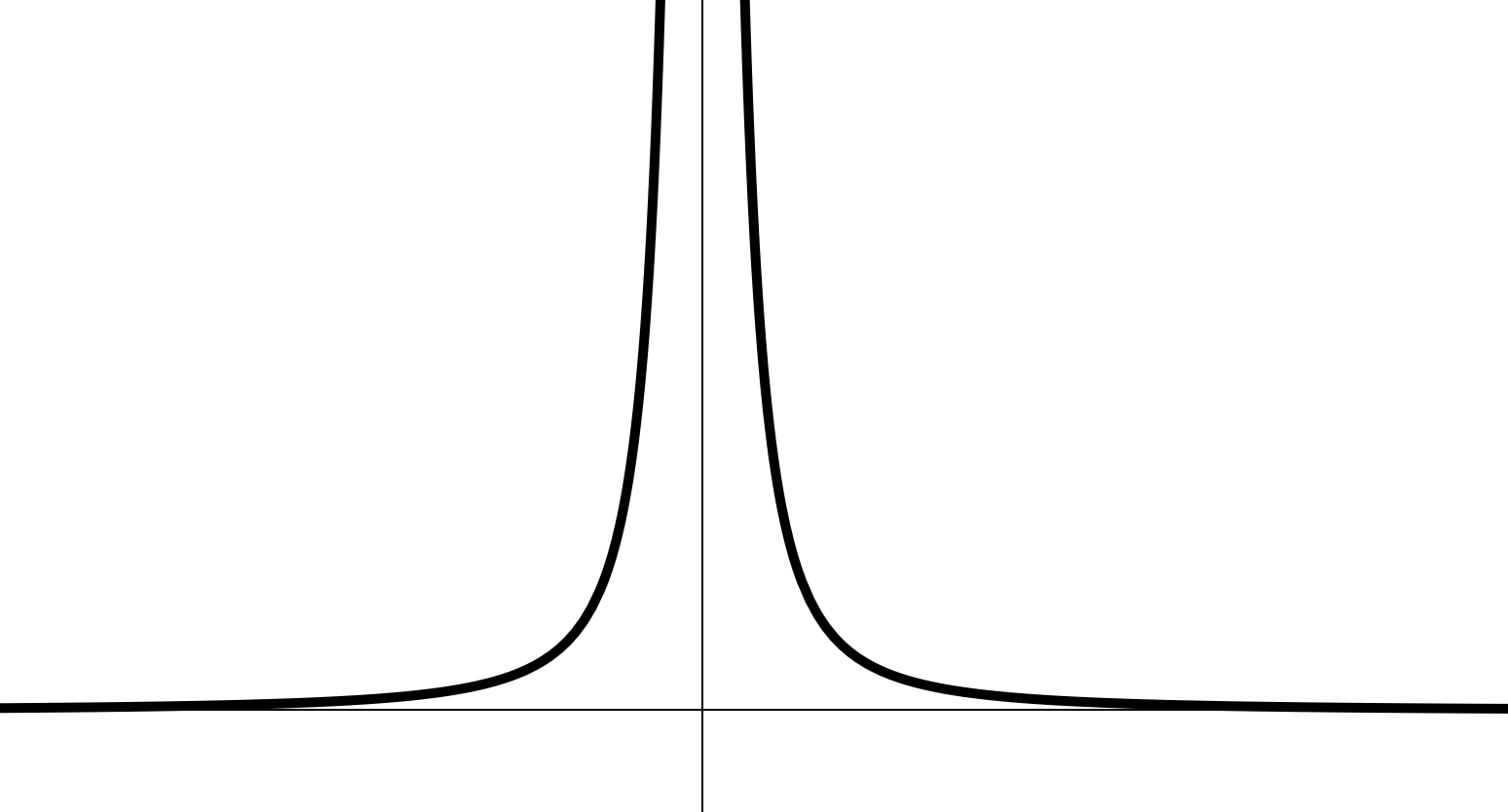
— четное:
- точек пересечения с осями нет
- неограниченная
- непериодическая
- нечетная
- асимптоты графика — оси координат
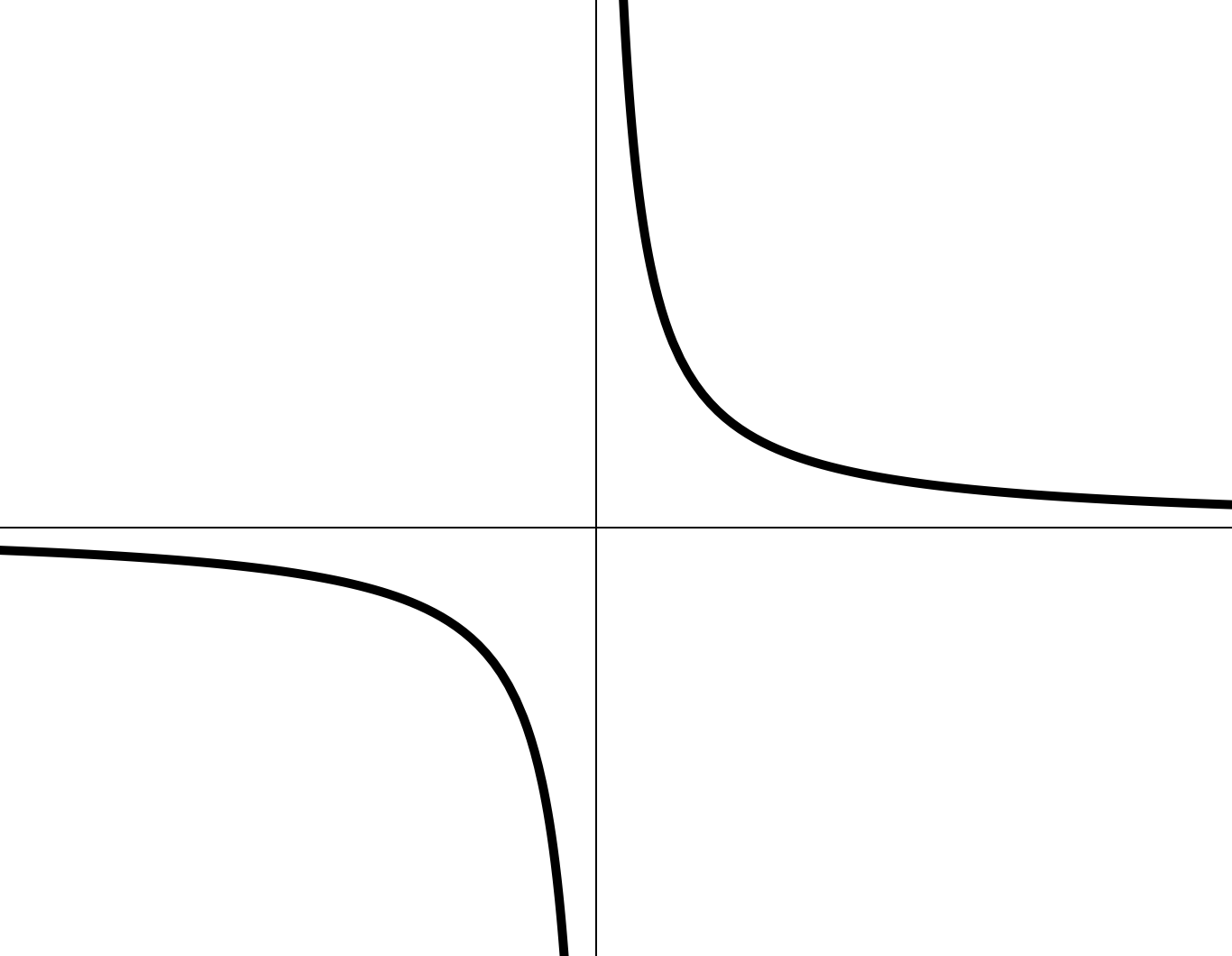
— нечетное:
I. Степенная функция (4)
Функция вида
— четное:

— нечетное:
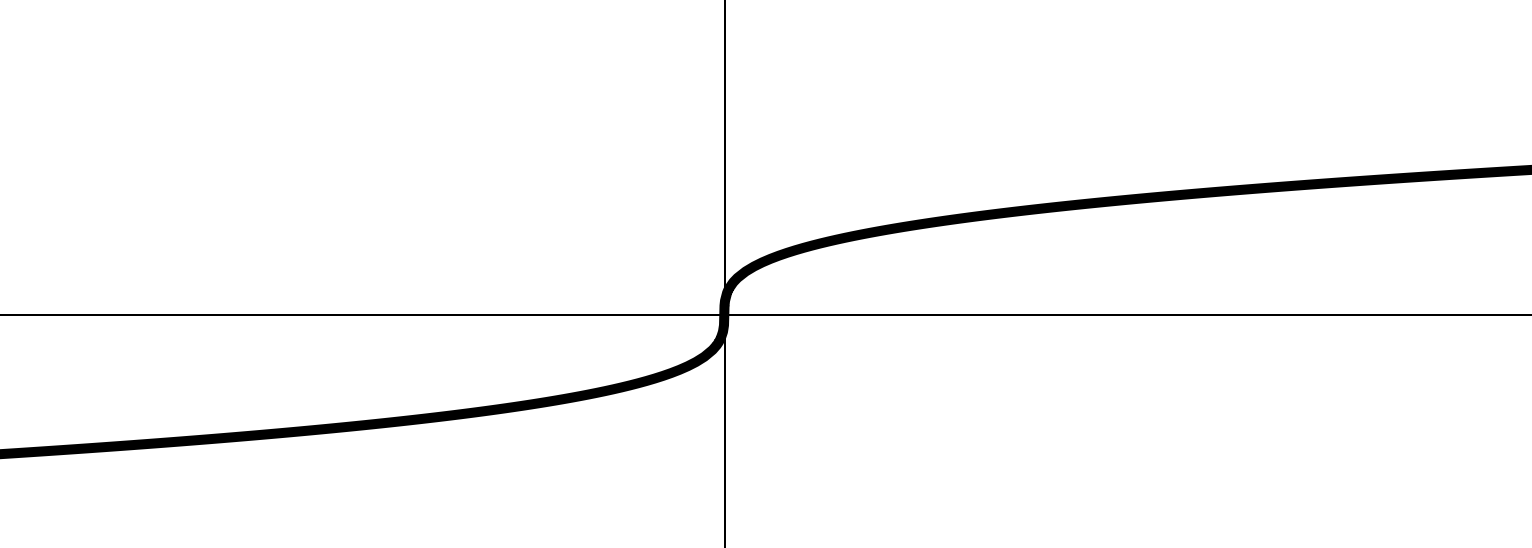
- т-ка пересеч. с осями координат:
- неограниченная
- непериодическая
- нечетная
- возрастающая
- функция обратимая
- т-ка пересеч. с осями координат:
- ограничена нулем снизу
- непериодическая
- нечетная
- возрастает на
- функция обратимая
II. Показательная функция
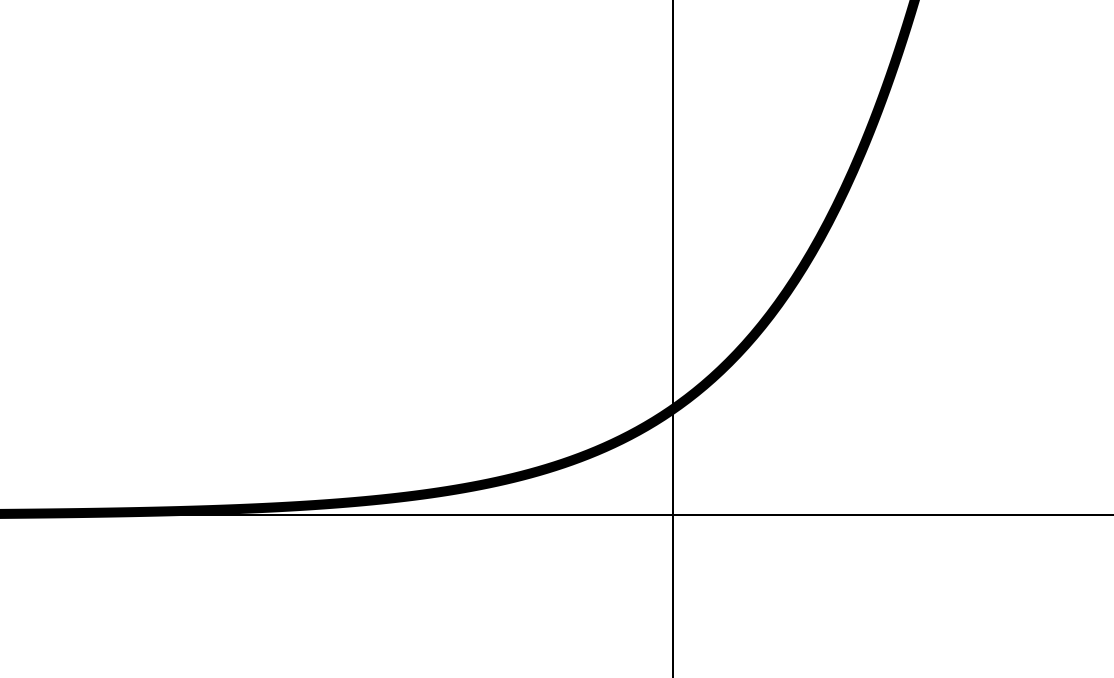
1.
- ;
- ;
- точка пересечения с осью ординат: ;
- непериодическая;
- возрастающая;
- обратимая;
- асимптота графика — ось абсцисс.
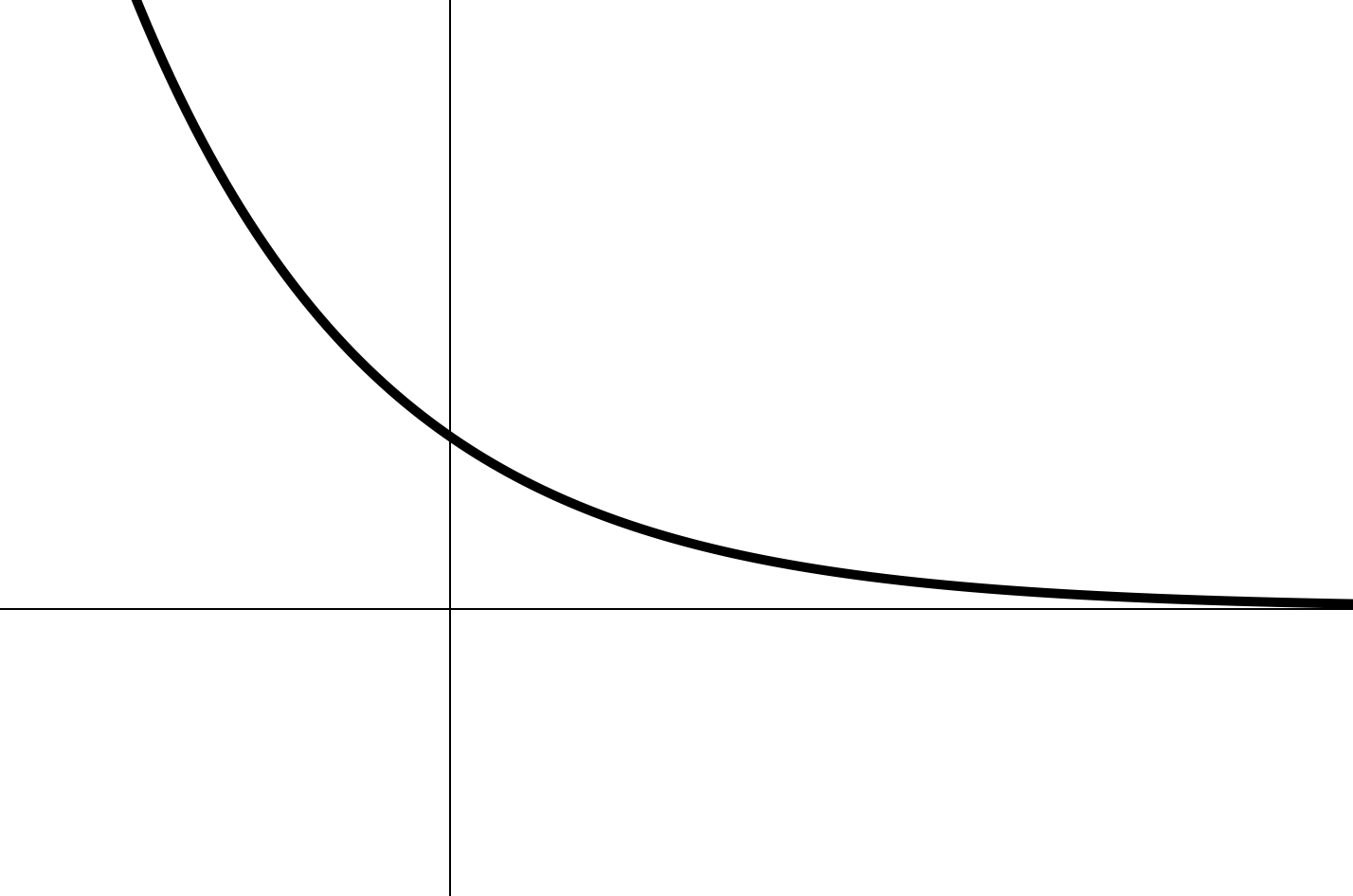
2.
- ;
- ;
- точка пересечения с осью ординат: ;
- непериодическая;
- убывающая;
- обратимая;
- асимптота графика — ось абсцисс.
II. Показательная функция (2)
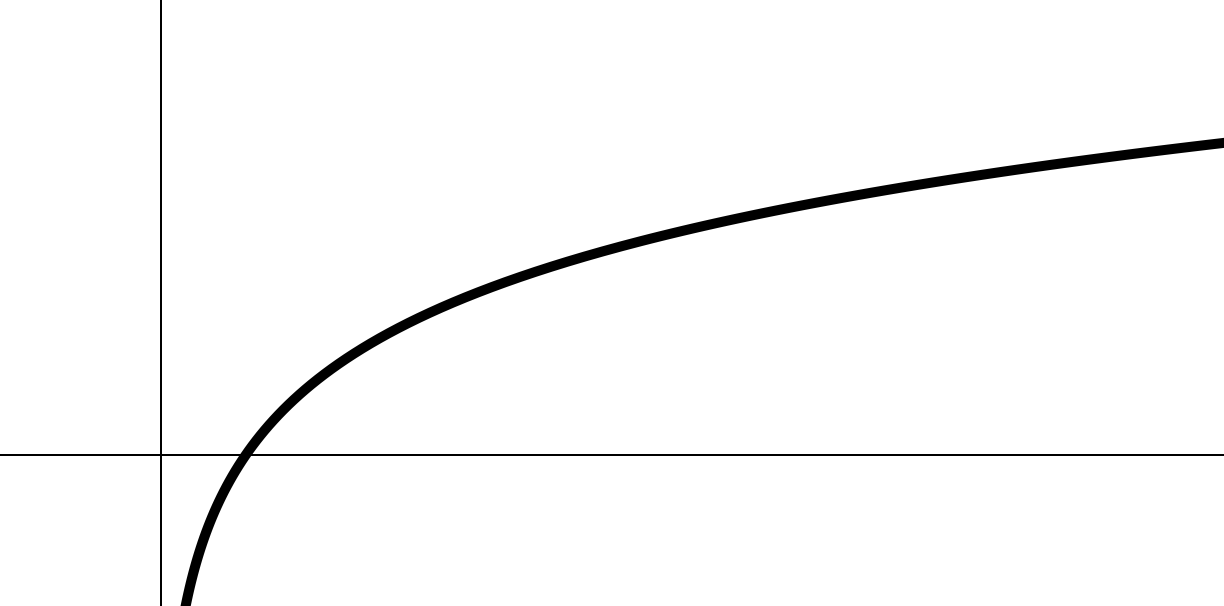
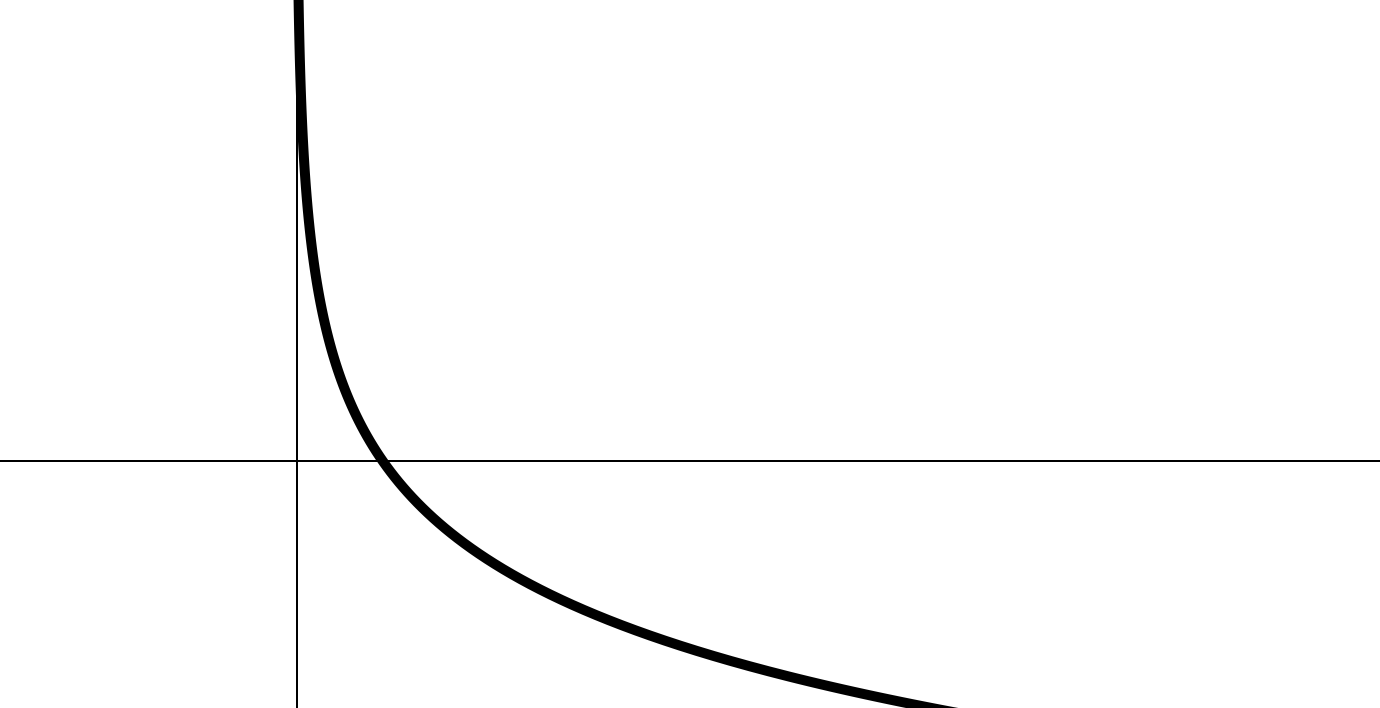
III. Логарифмическая функция
1.
- ;
- ;
- точка пересечения с осью абсцисс: ;
- неограниченная
- непериодическая;
- возрастающая;
- обратимая;
- асимптота графика — ось ординат.
III. Логарифмическая функция (2)
2.
- ;
- ;
- точка пересечения с осью абсцисс: ;
- неограниченная
- непериодическая;
- убывающая;
- обратимая;
- асимптота графика — ось ординат.
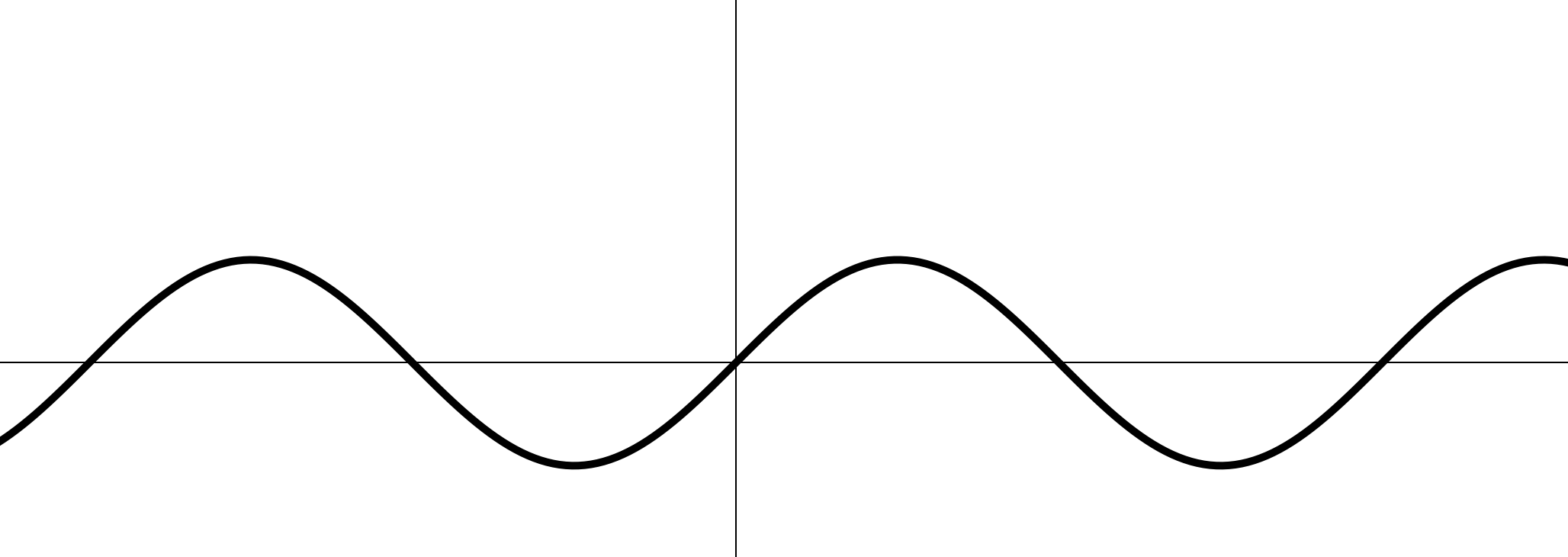
IV. Тригонометрические функции
1.
- ;
- ;
-
точка пересечения с осями:
- с : .
- с : ;
- ограничена: ;
- периодическая: ;
- нечетная;
- возрастает на:
- убывает на:
- необратимая.
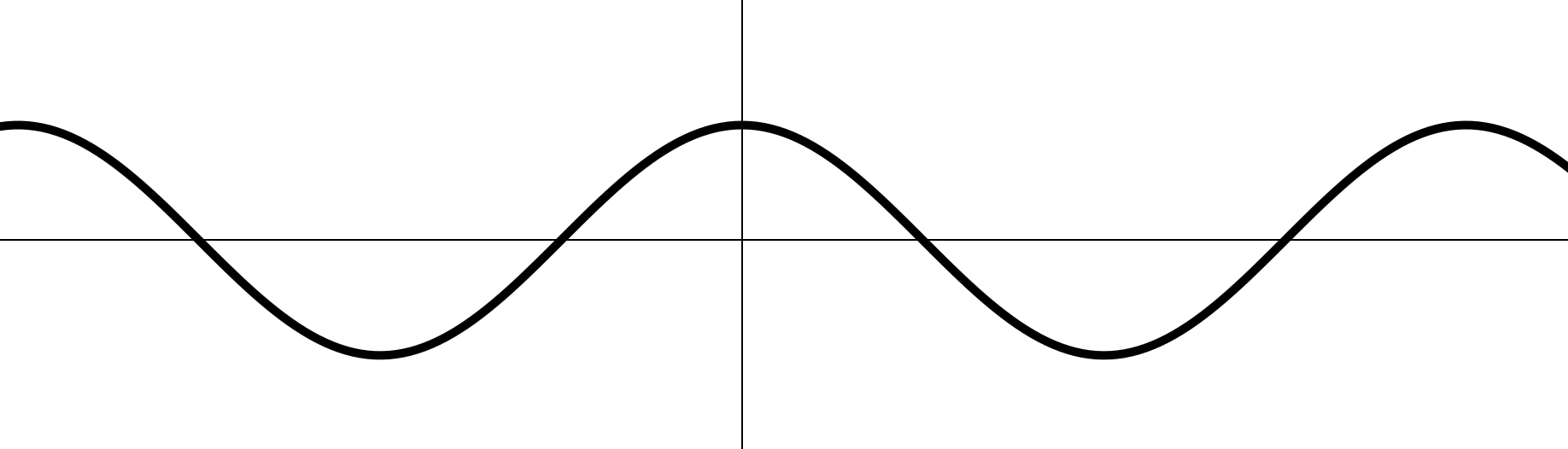
IV. Тригонометрические функции (2)
2.
- ;
- ;
-
точка пересечения с осями:
- с :
- с : ;
- ограничена: ;
- периодическая: ;
- четная;
- возрастает на:
- убывает на:
- необратимая.
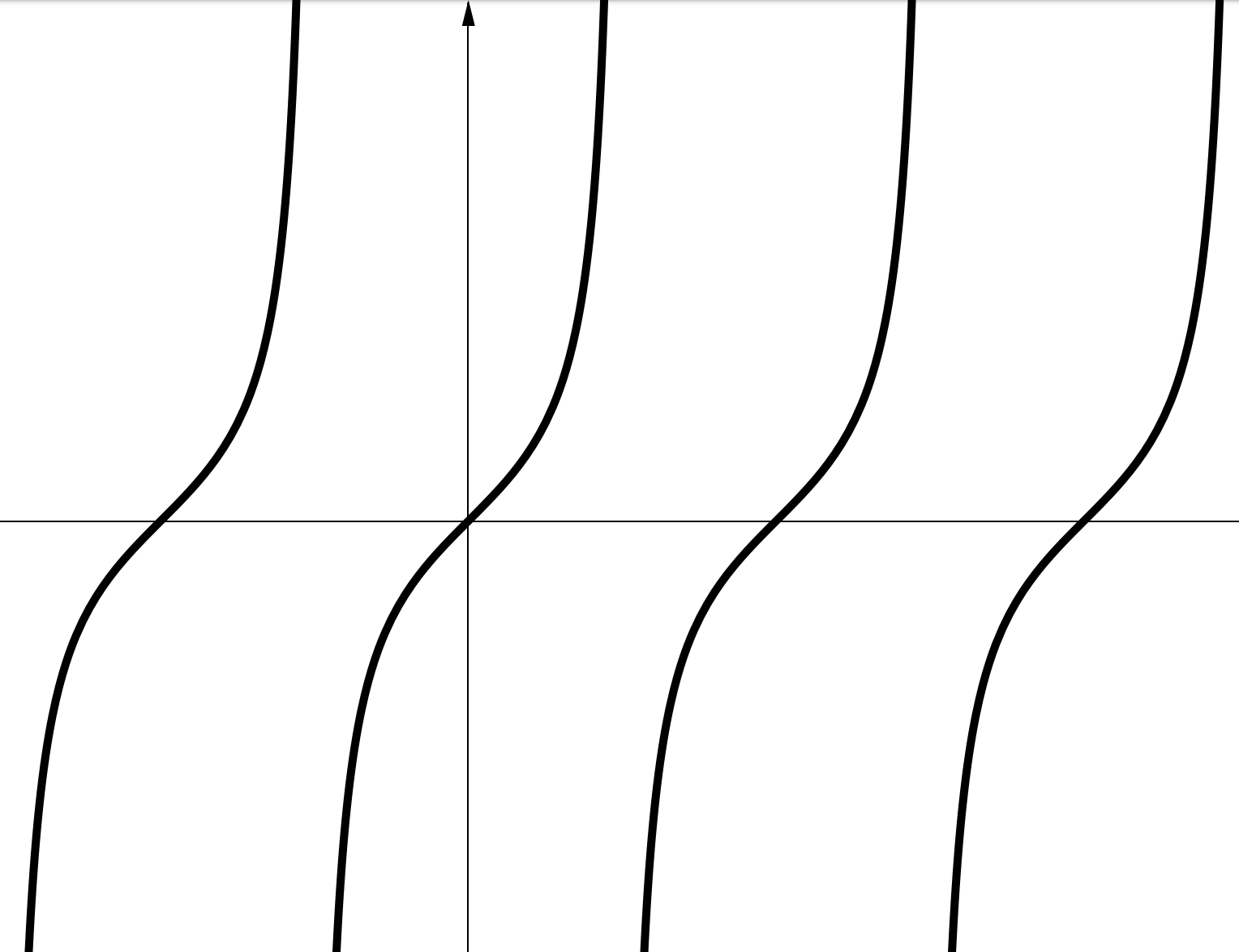
IV. Тригонометрические функции (3)
3.
- ;
- ;
-
точка пересечения с осями:
- с :
- с : ;
- неограниченная;
- периодическая: ;
- нечетная;
- возрастает на:
- необратимая;
- асимптоты:
IV. Тригонометрические функции (4)
4.
- ;
- ;
-
точка пересечения с осями:
- с :
- неограниченная;
- периодическая: ;
- нечетная;
- убывает на:
- необратимая;
- асимптоты:
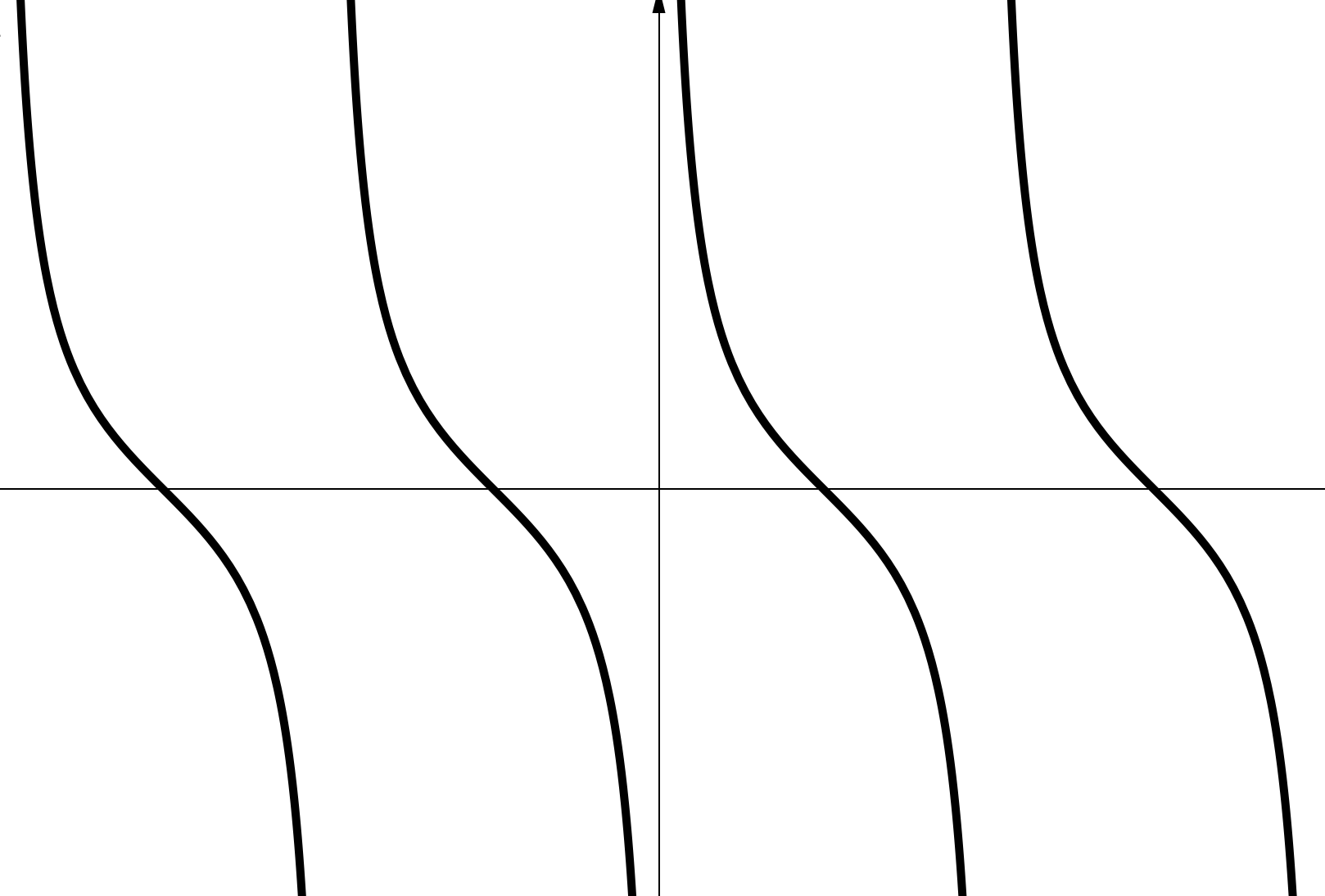
V. Обратные тригонометрические функции
1.
- ;
- ;
- точка пересечения с осями: ;
- ограничена: ;
- нечетная;
- возрастающая.
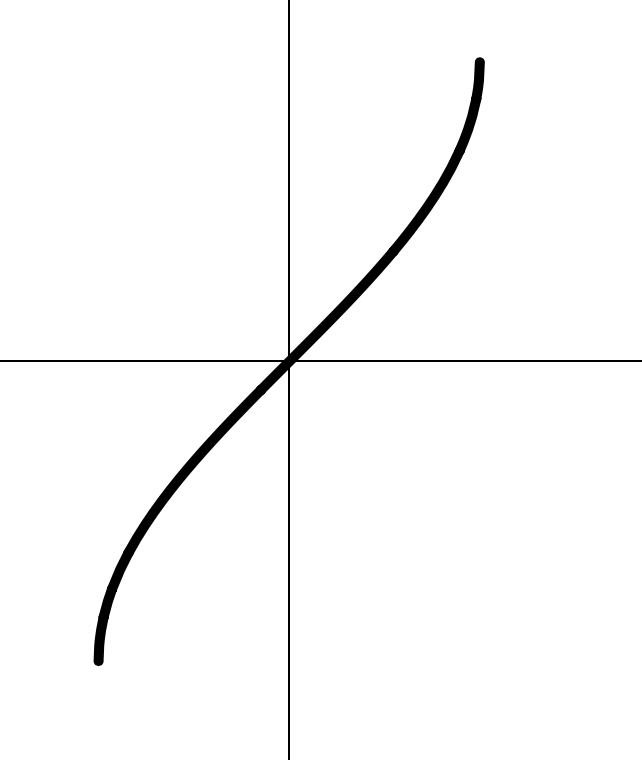
2.
- ;
-
точка пересечения с осями:
- с : ; с :
- ограничена: ;
- убывающая;
- обратимая.
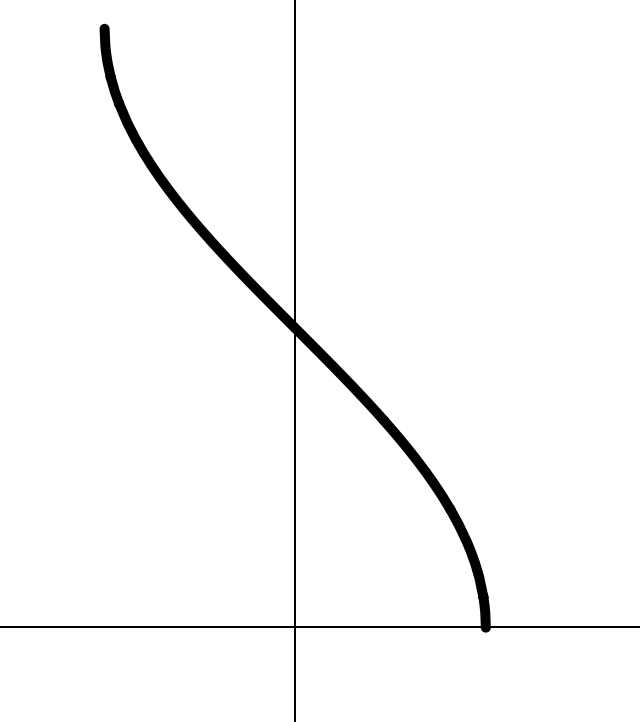
V. Обратные тригонометрические функции (2)
3.
- ;
- ;
- точка пересечения с осями: ;
- ограничена: ;
- нечетная; возрастающая; обратимая;
- асимптоты:
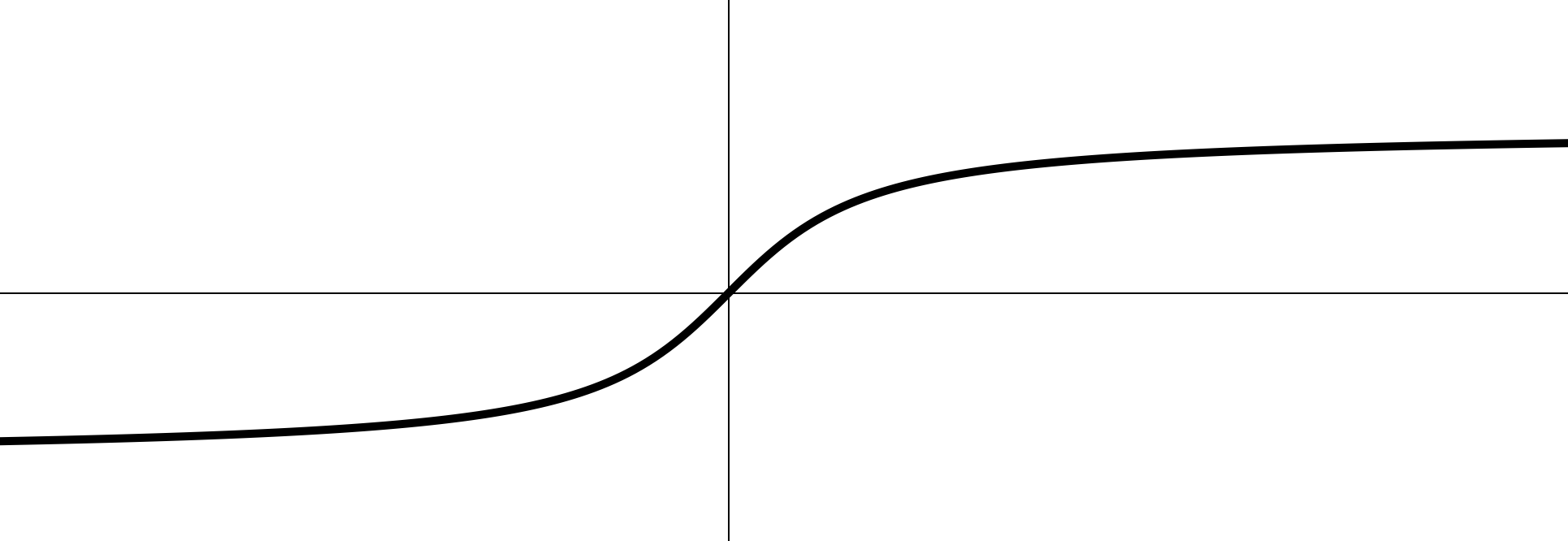
4.
- ;
- точка пересечения с :
- ограничена: ;
- убывающая;
- обратимая;
- асимптоты:

Преобразования графиков функций
- преобразования аргумента: если в функции присутствует несколько преобразований, последовательность преобразований аргумента происходит в «обратном» порядке по сравнению с обычными арифметическими действиями:
1. Вычленение базовой функции, собственно, график которой мы преобразовываем.
2. Определения порядка преобразований:
- преобразования со смещениями по ; преобразования со внешними модулями, если таковые имеются:
Задача 1
Построить эскиз графика функции .
Решение:
1. Цепочка элементарных преобразований:
2. Построение:
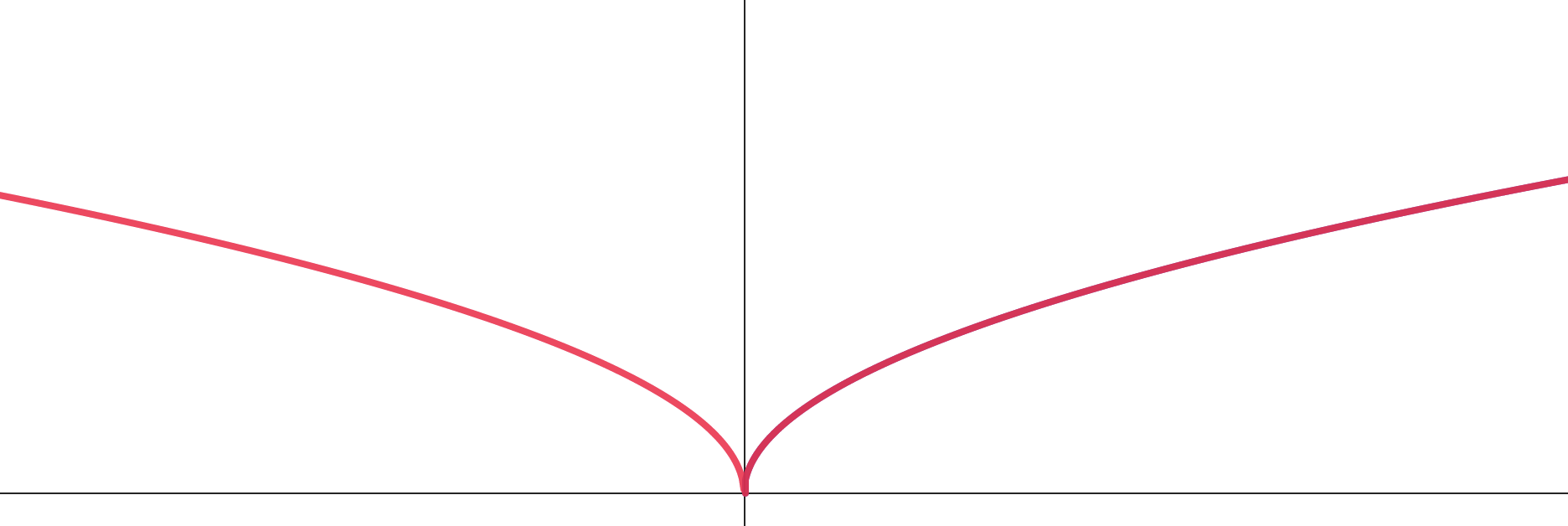
Часть графика, расположенную левее оси стираем, часть графика, расположенную правее оси достраиваем симметрично относительно .
Задача 1. Продолжение
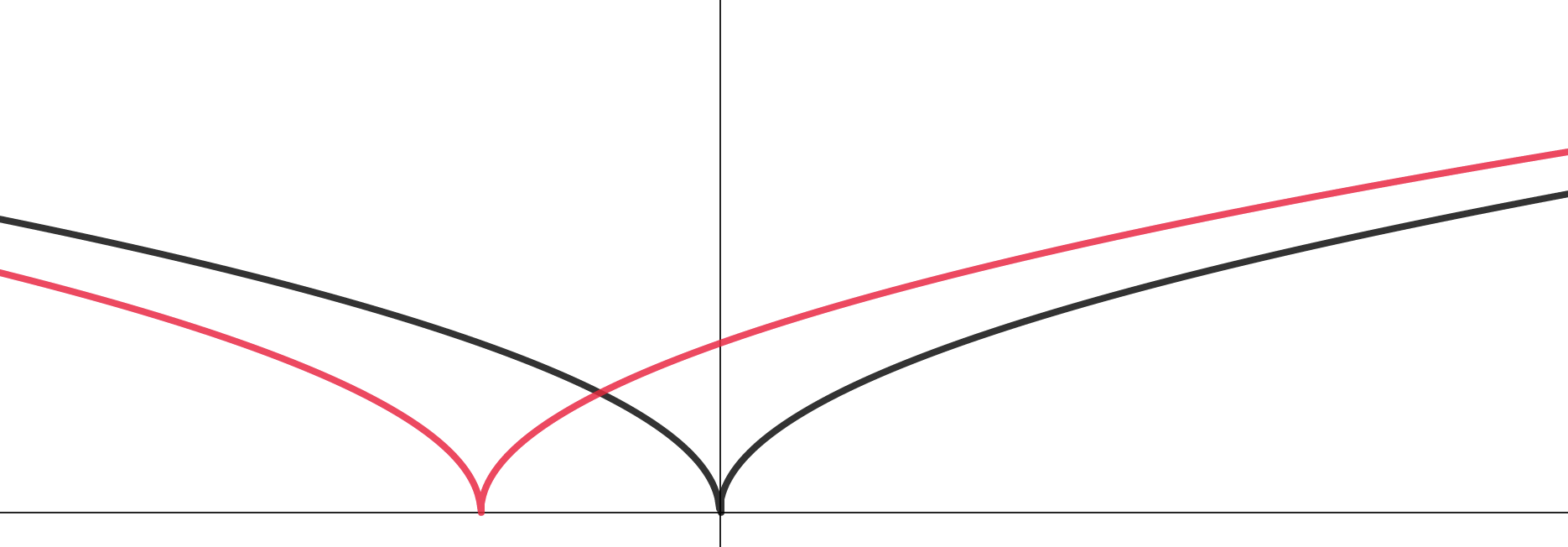
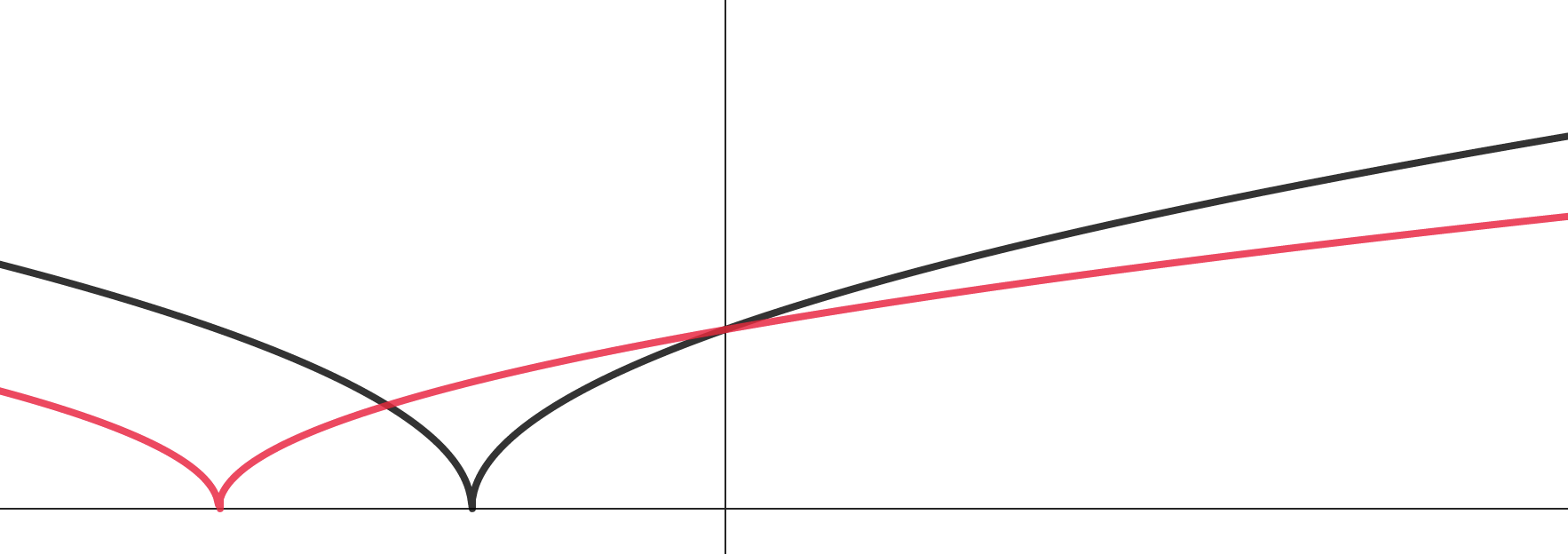
Переносим на 2 единицы по
влево.
Растягиваем в 2 раза по
Растягиваем в 2 раза по
Задача 1. Продолжение (2)
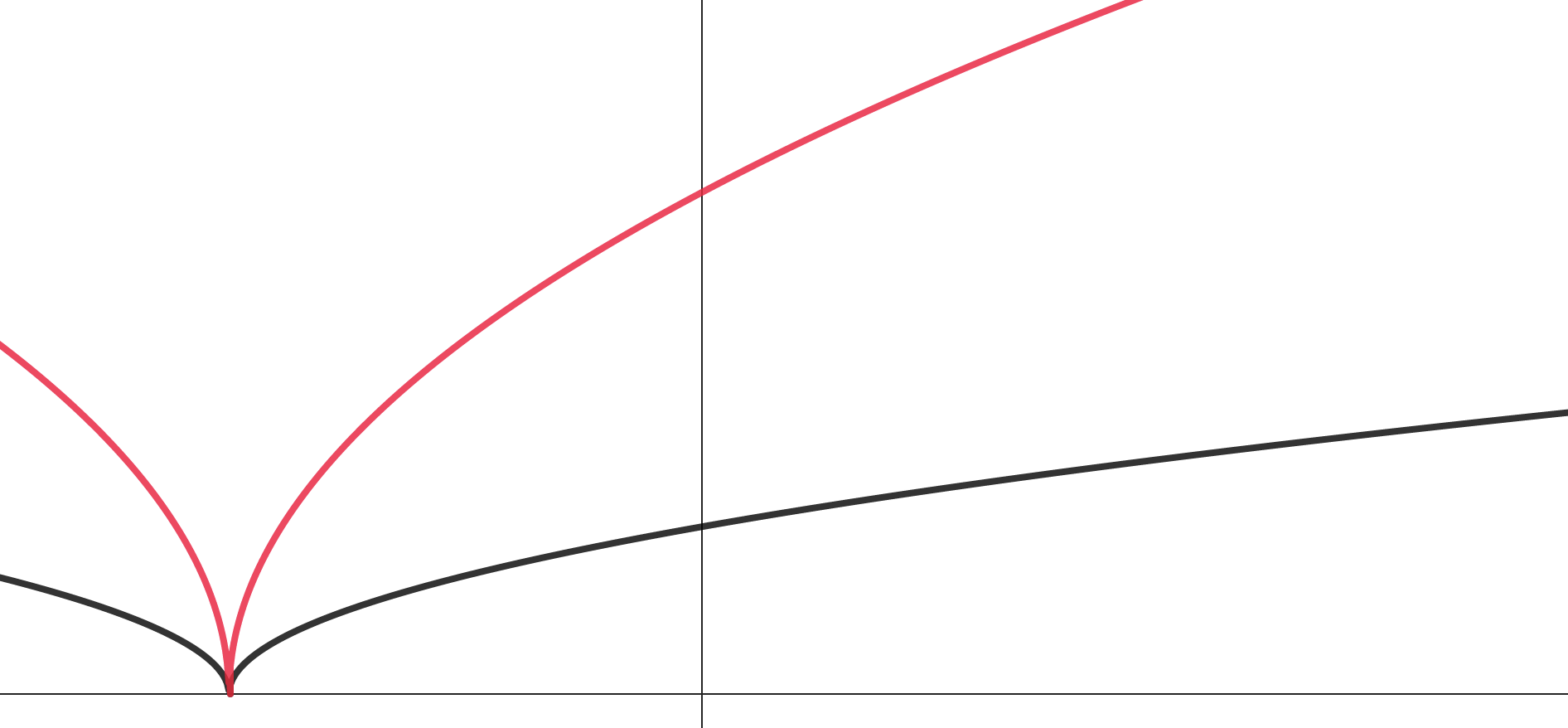
Растягиваем в 3 раза
по
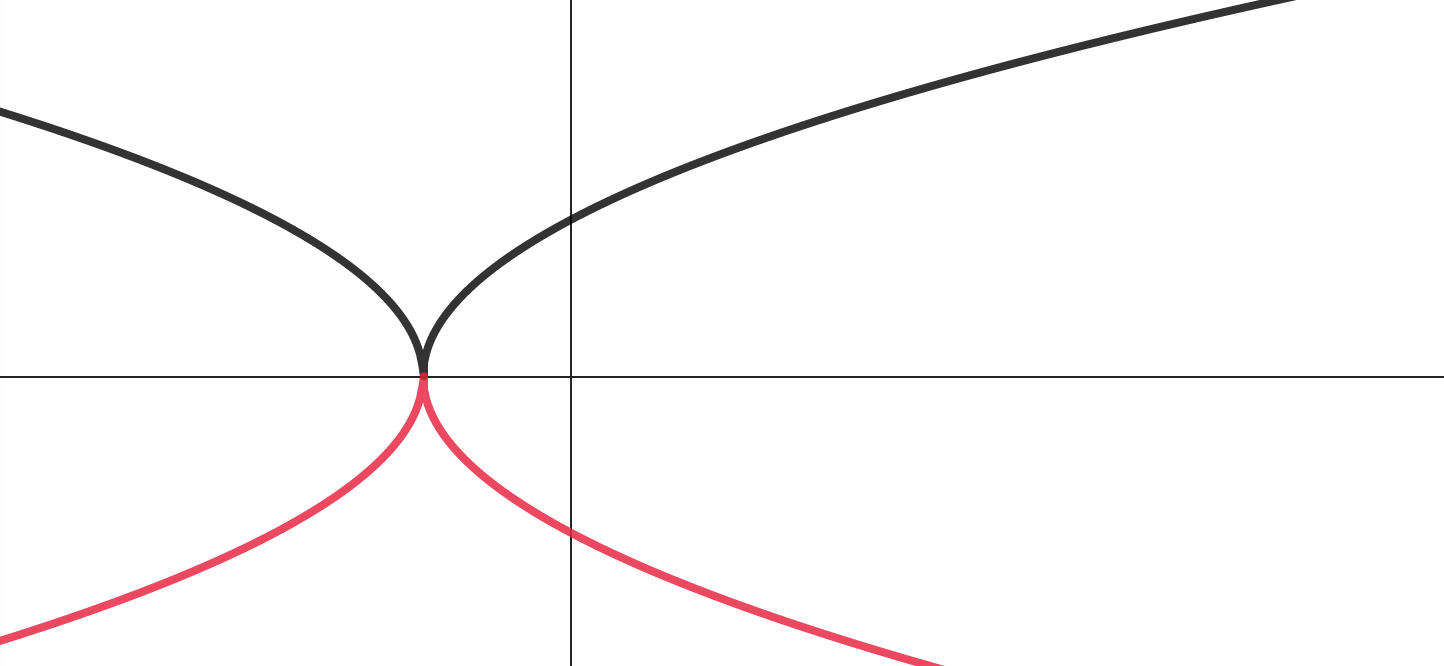
Зеркально
отражаем график относительно .
Задача 1. Продолжение (3)
Часть графика, расположенную выше оси оставляем без изменений, часть графика, расположенную ниже оси , отображаем симметрично относительно этой оси.
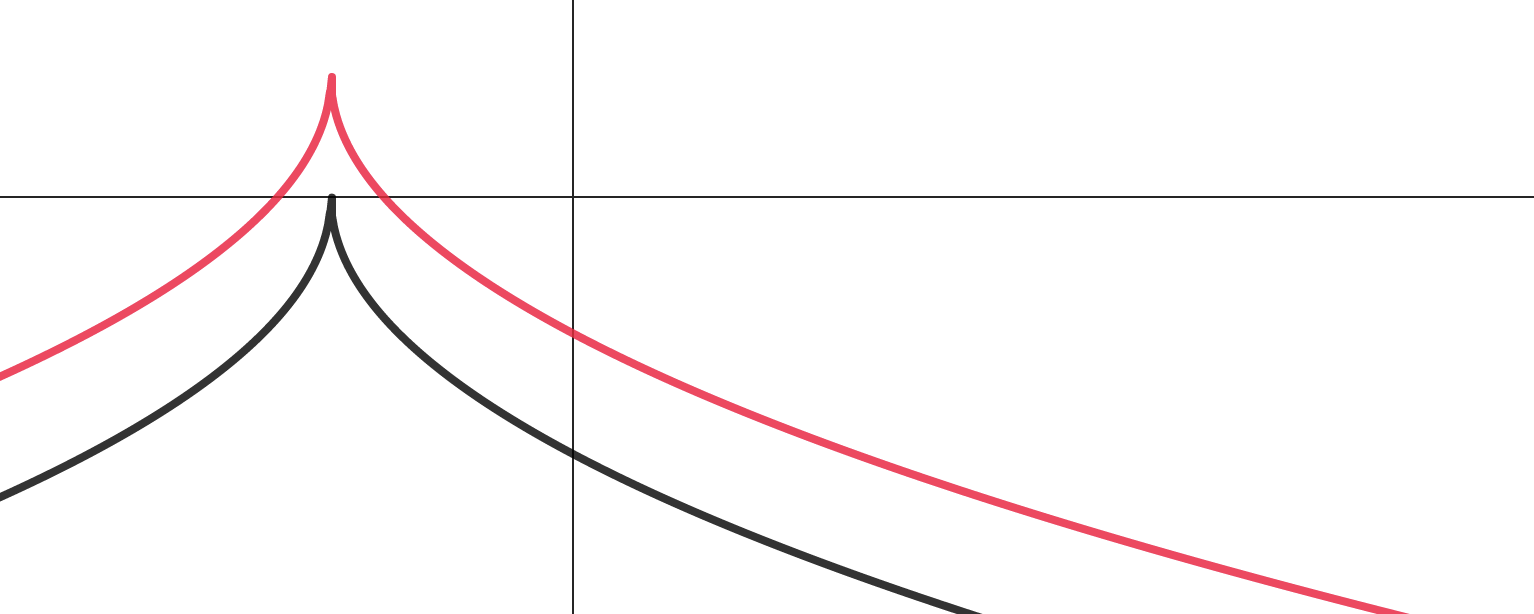
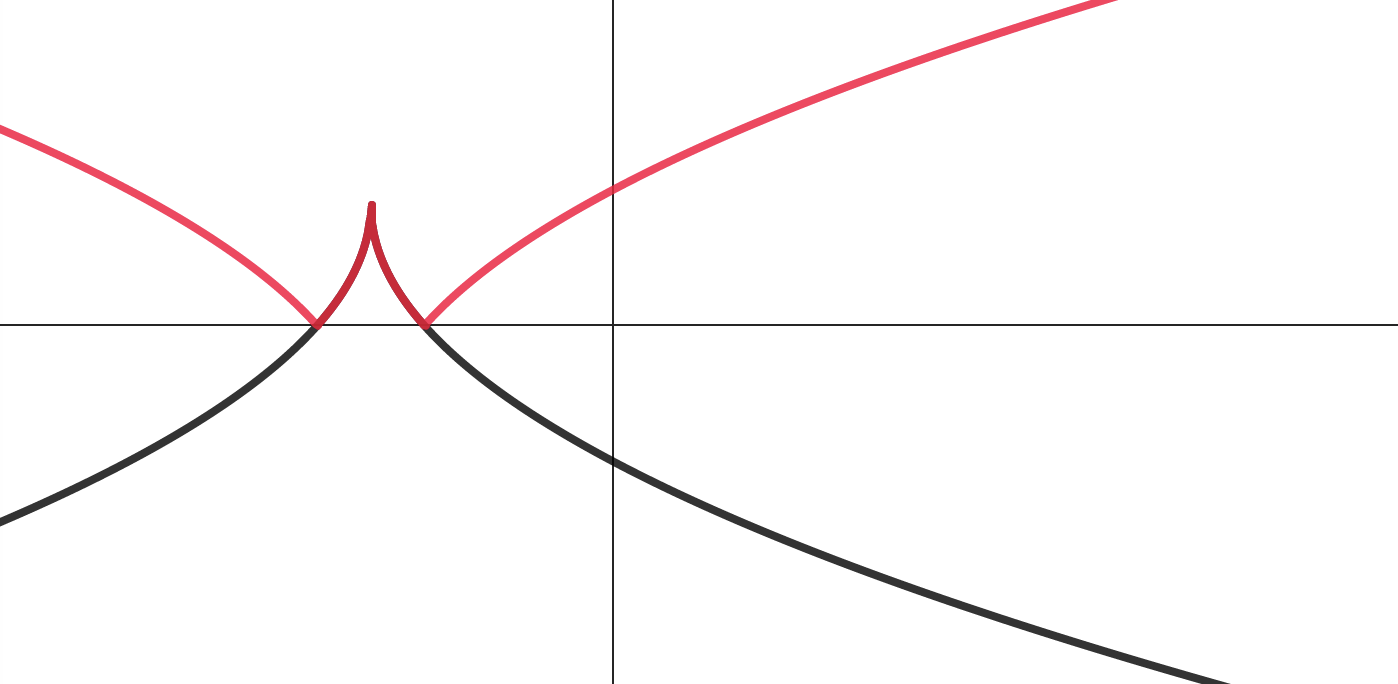
Переносим на две единицы вверх по .
Задача 2
Построить эскиз графика функции .
Решение:
1. Цепочка элементарных преобразований:
2. Построение:
Переносим на влево по
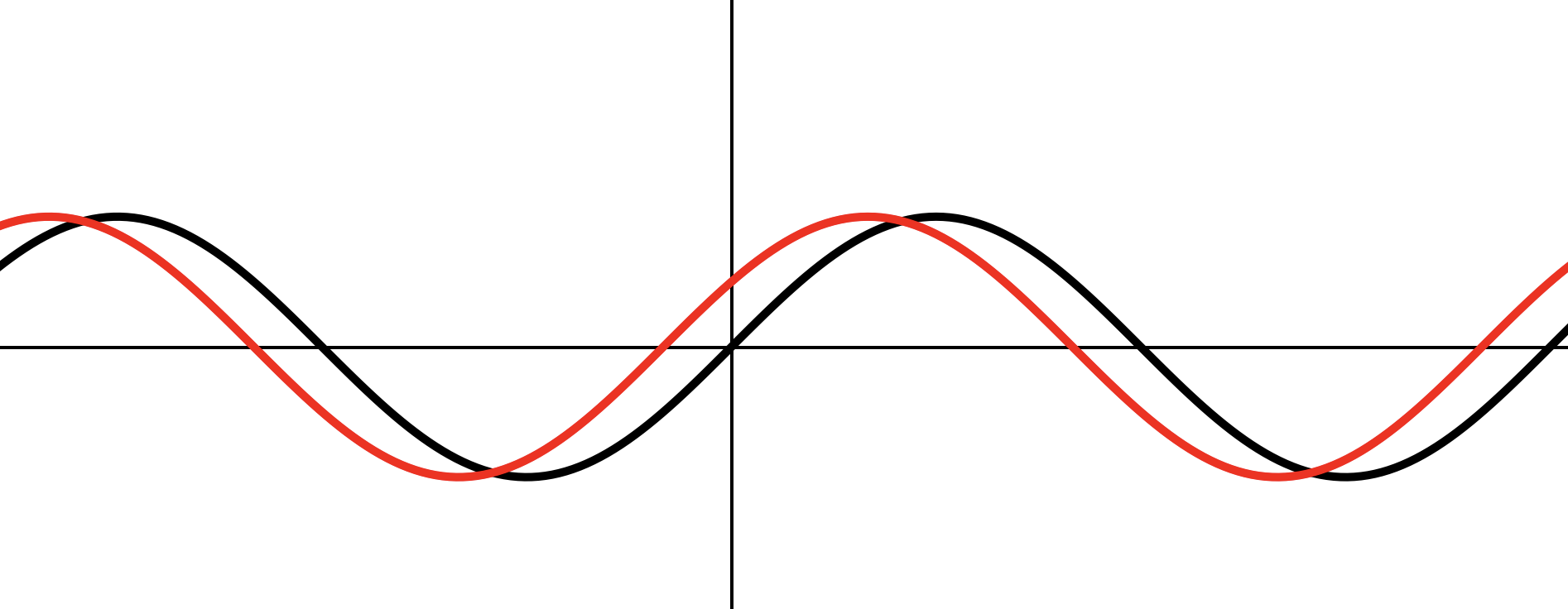
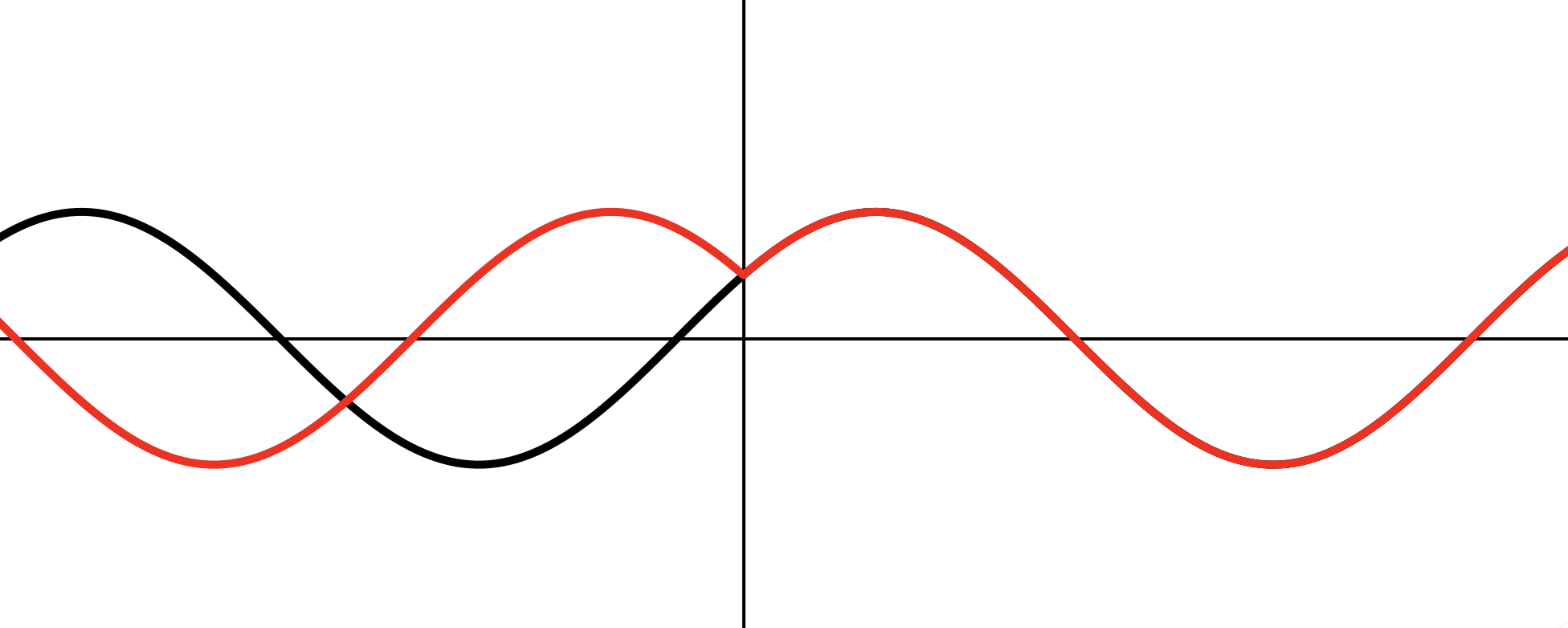
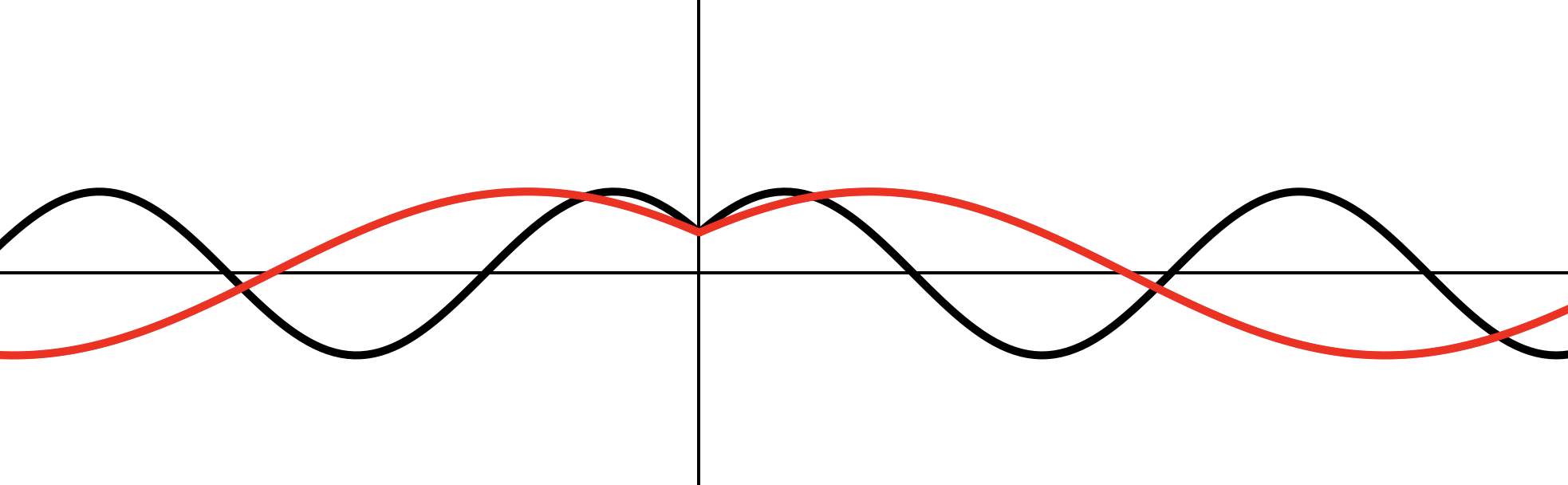
Отражаем часть графика на зеркально относительно . Часть графика на стираем.
Растягиваем в 2
раза по .
Задача 2 (продолжение)
Зеркально
отражаем график относительно .
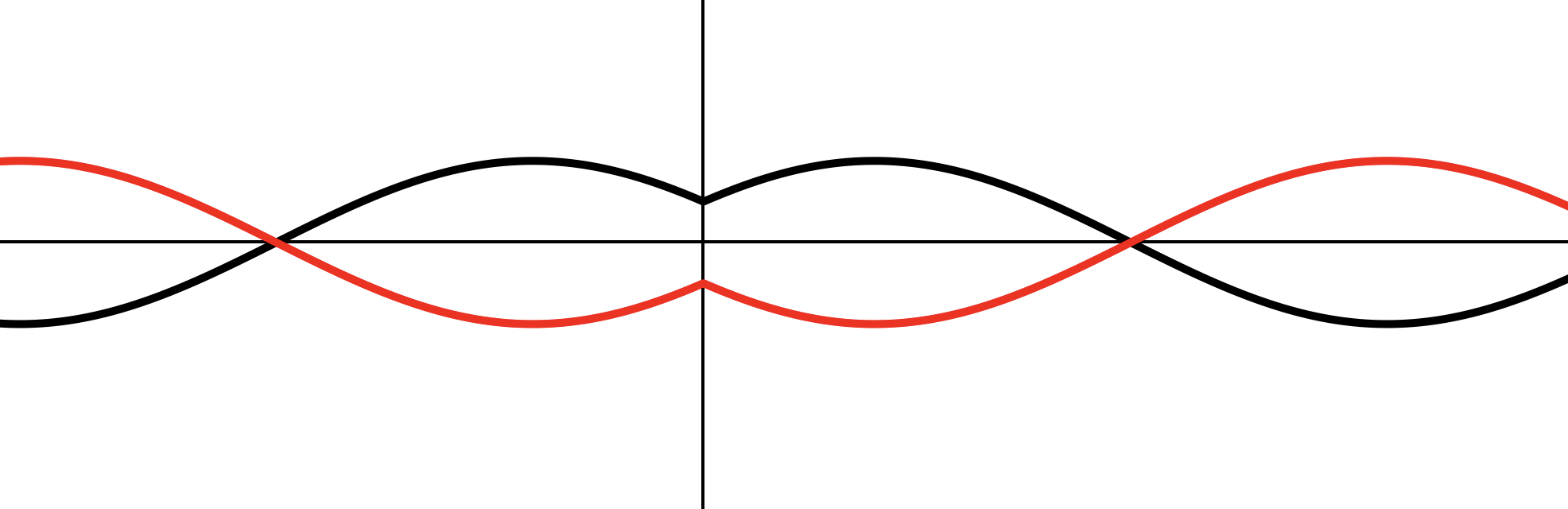
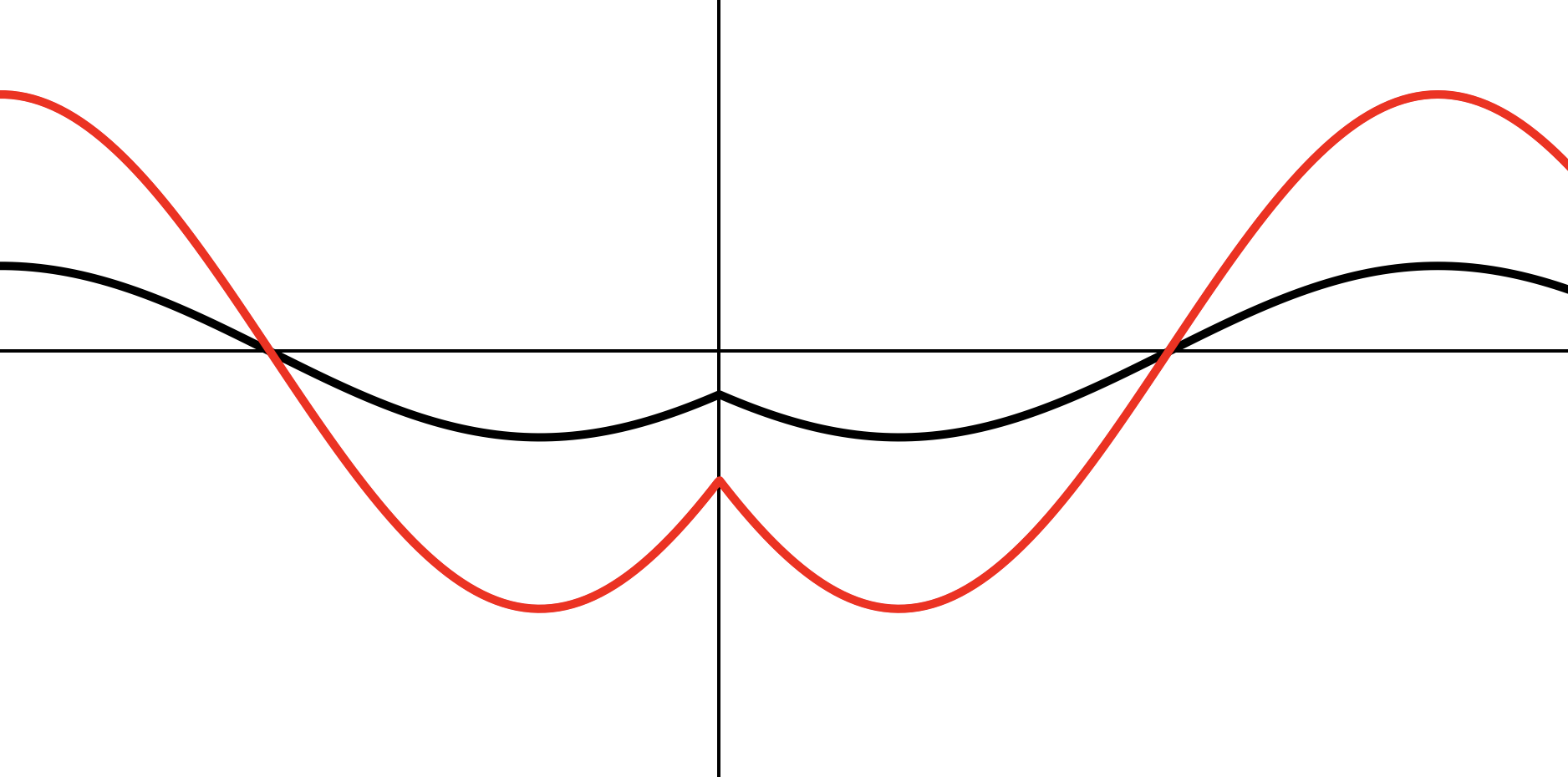
в 3 раза по .
Задача 2 (продолжение) (2)
Растягиваем
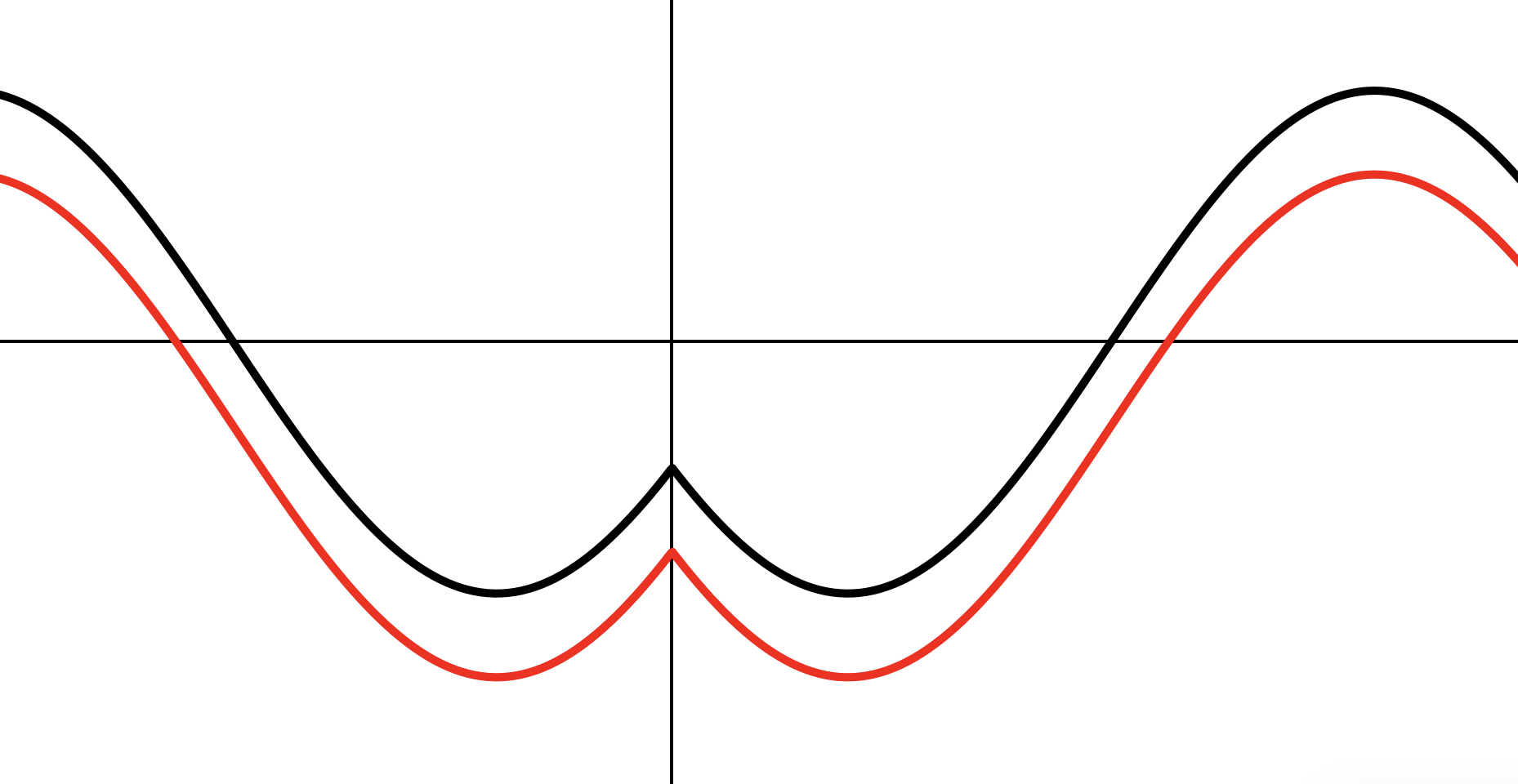
Переносим на единицу вниз по .
Задача 3 (более общие преобразования)
Построить эскиз графика функции .
Решение:
1. Цепочка элементарных преобразований:
2. Построение:
Симметрично отражаем относительно
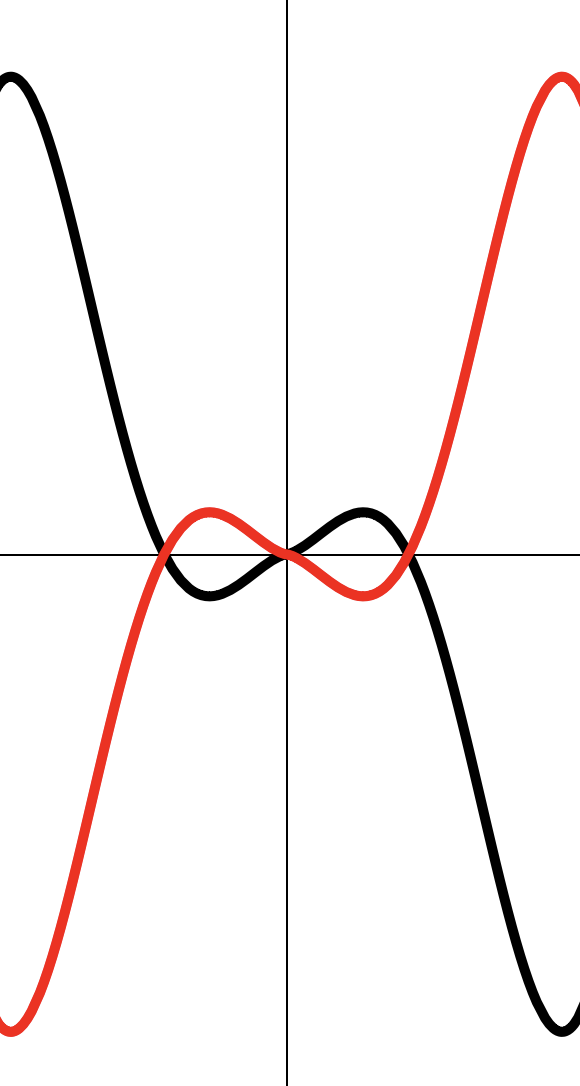
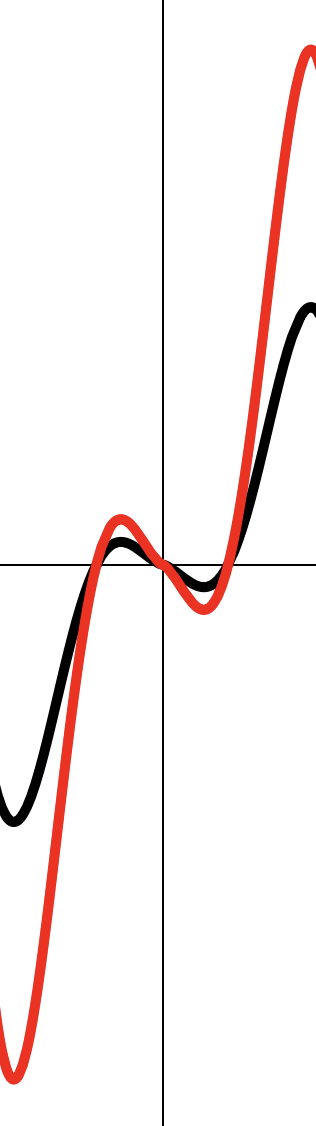
Растягиваем в 2 раза вдоль .
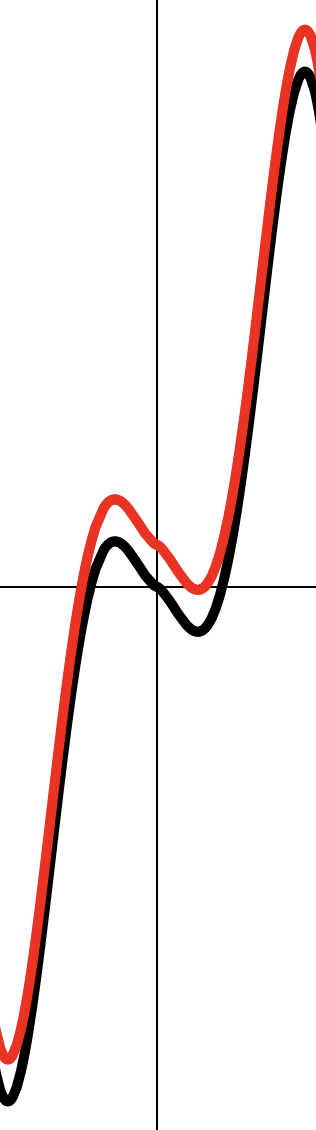
Поднимаем на одну единицу вверх по .
Задачи
Построить эскизы следующих графиков функций с помощью элементарных преобразований:
а)
в)
г)
д)
е)
б)
ж)
и)
й)
к)
л)
з)
График дробно-линейной функции
Частные случаи:
1)
2)
Общий случай:
(График — прямая)
(График — прямая, параллельная ).
Пример:
Пример:

Построение графика дробно-линейной ф-ии (I)
(I способ) С помощью элементарных преобразований:
главная часть (целая часть)
дробная часть
Пример:
Цепочка элементарных преобразований:
Построение графика дробно-линейной ф-ии (I-2)
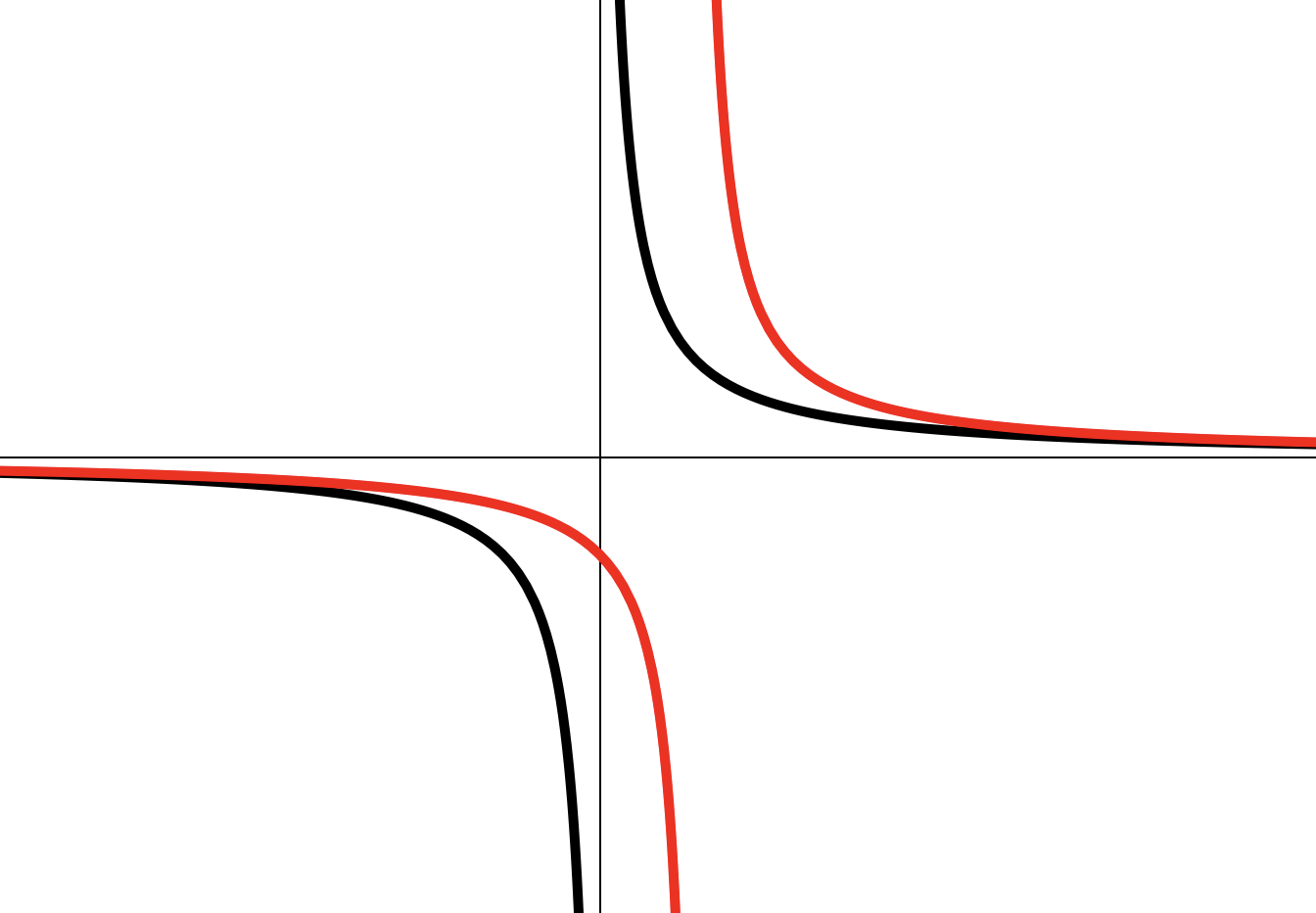
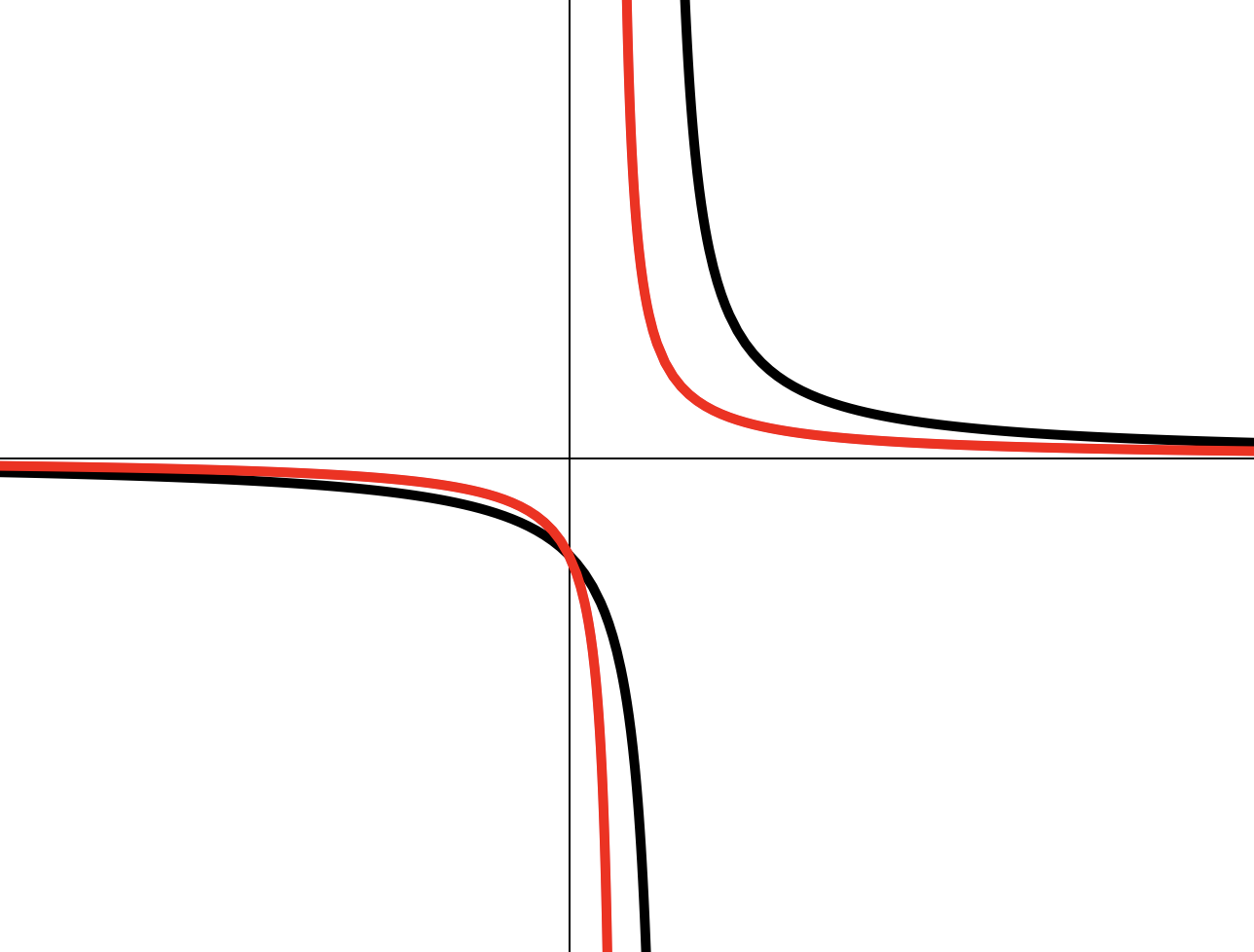
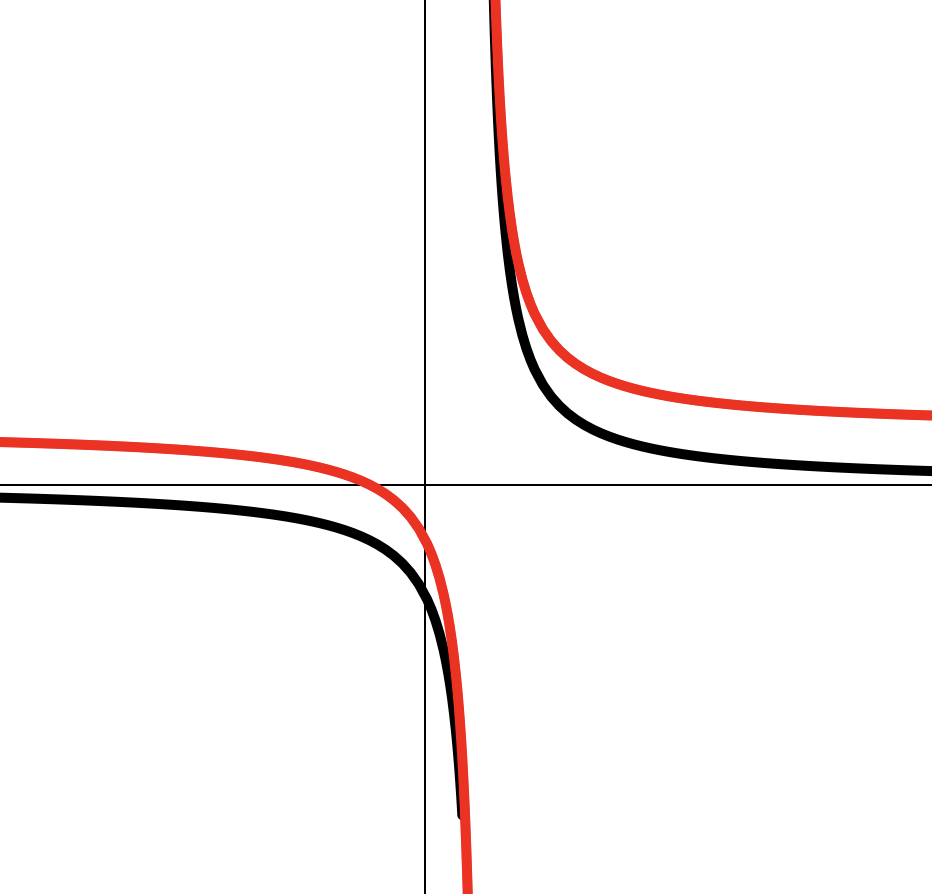
Сдвигаем на единицу влево по .
Сжимаем по в 2 раза.
Сдвигаем на одну единицу вверх по .
Построение графика дробно-линейной ф-ии (II)
(II способ) С помощью асимптот:
(Вертикальная асимптота)
(Горизонтальная асимптота)
Пример:
1. Горизонтальная асимптота:
2. Вертикальная асимптота:
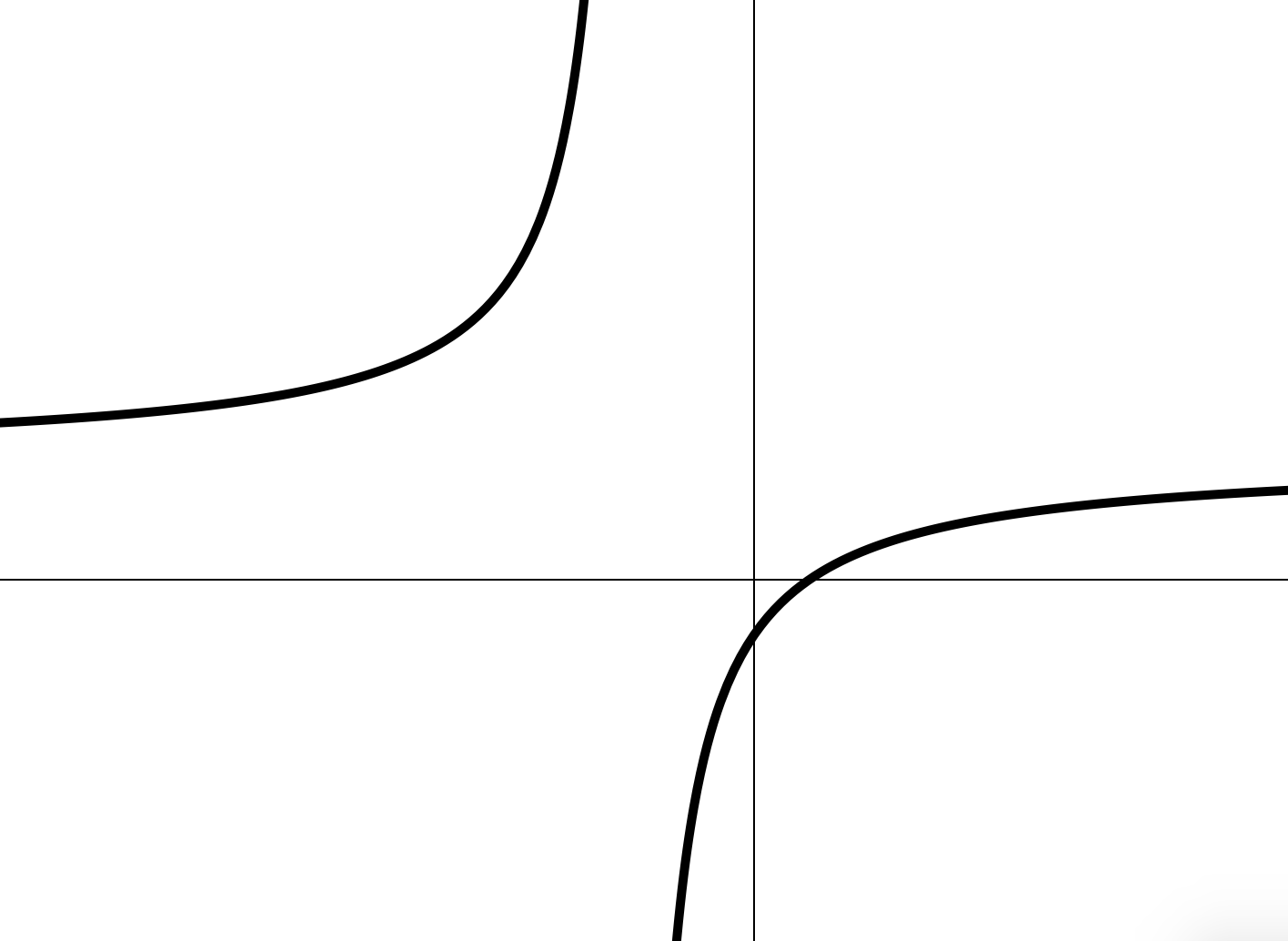
Задача 4
Построить эскиз графика функции с помощью элементарных преобразований и методом асимптот.
Задача 5
Построить эскиз графика функции с помощью элементарных преобразований и методом асимптот.
Задача 6
Найти множество значений функции
1. Цепочка элементарных преобразований:
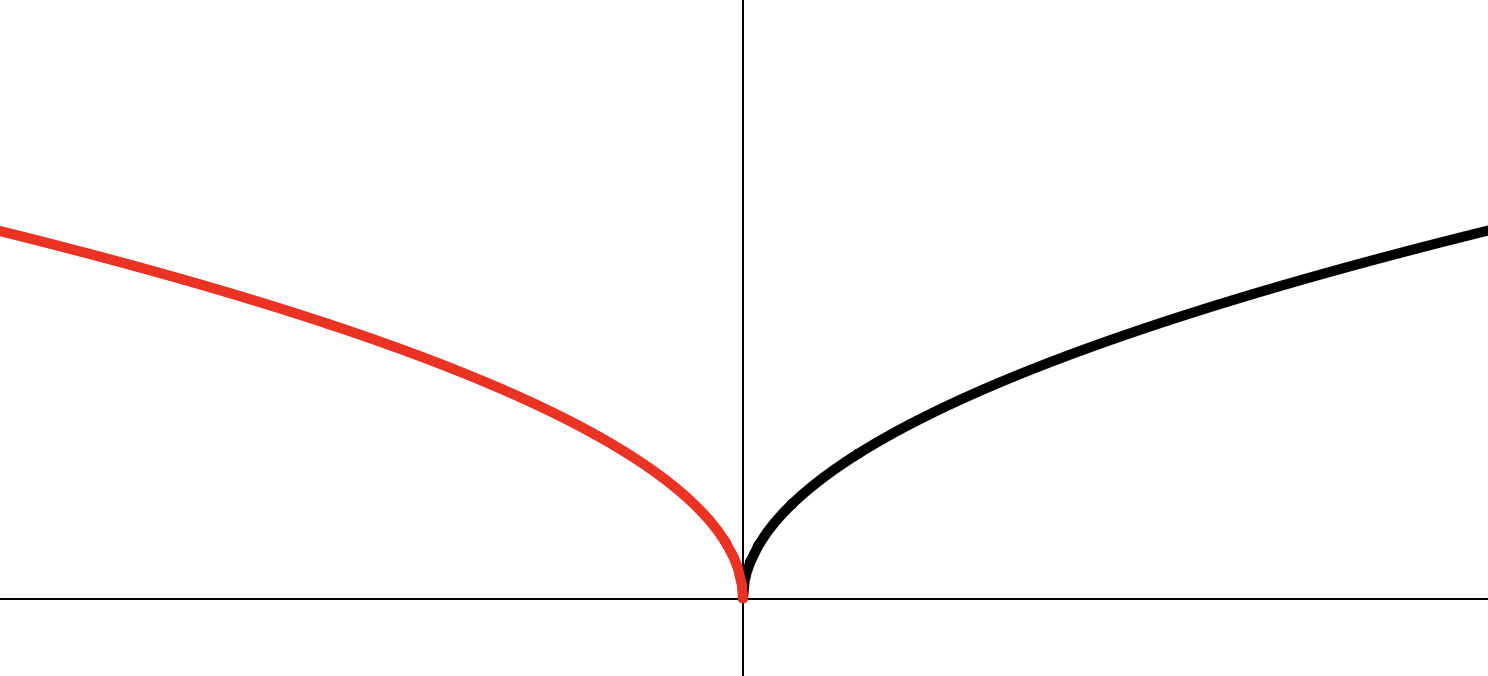
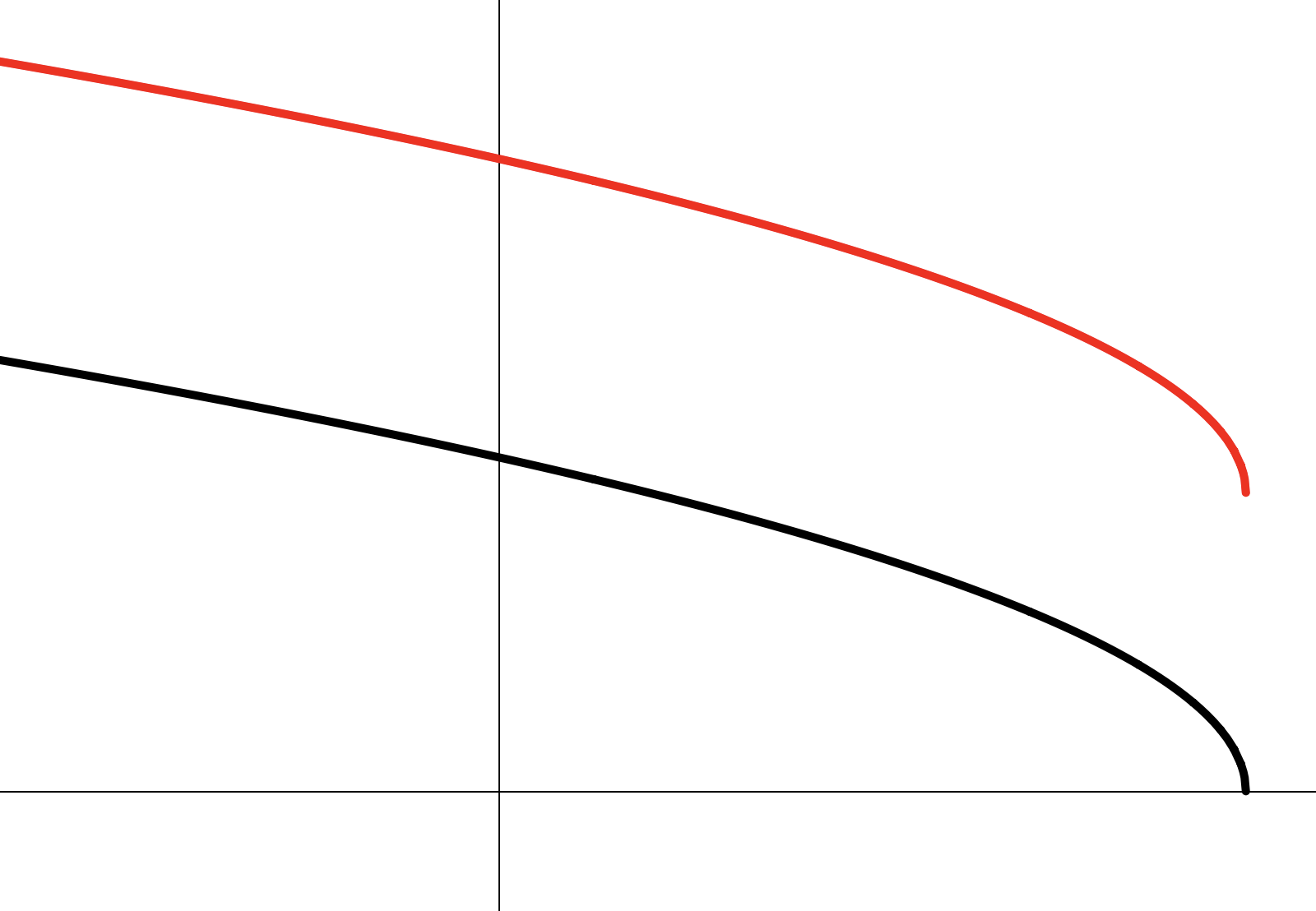
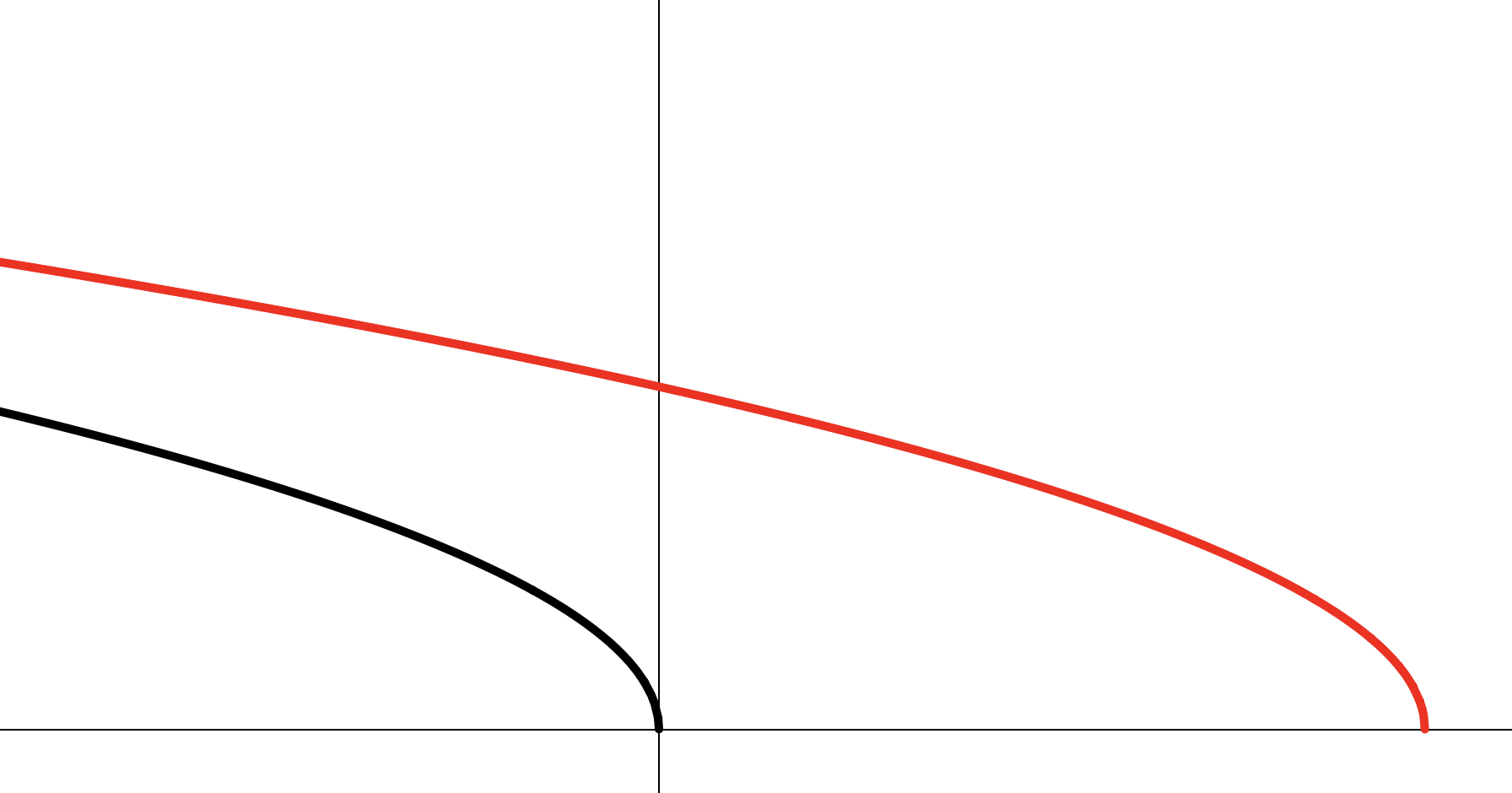
2. Построение:
I. Графически:
II. Аналитически:
FIX IT!
Построение графиков вида
Пример 1
Построить эскиз графика
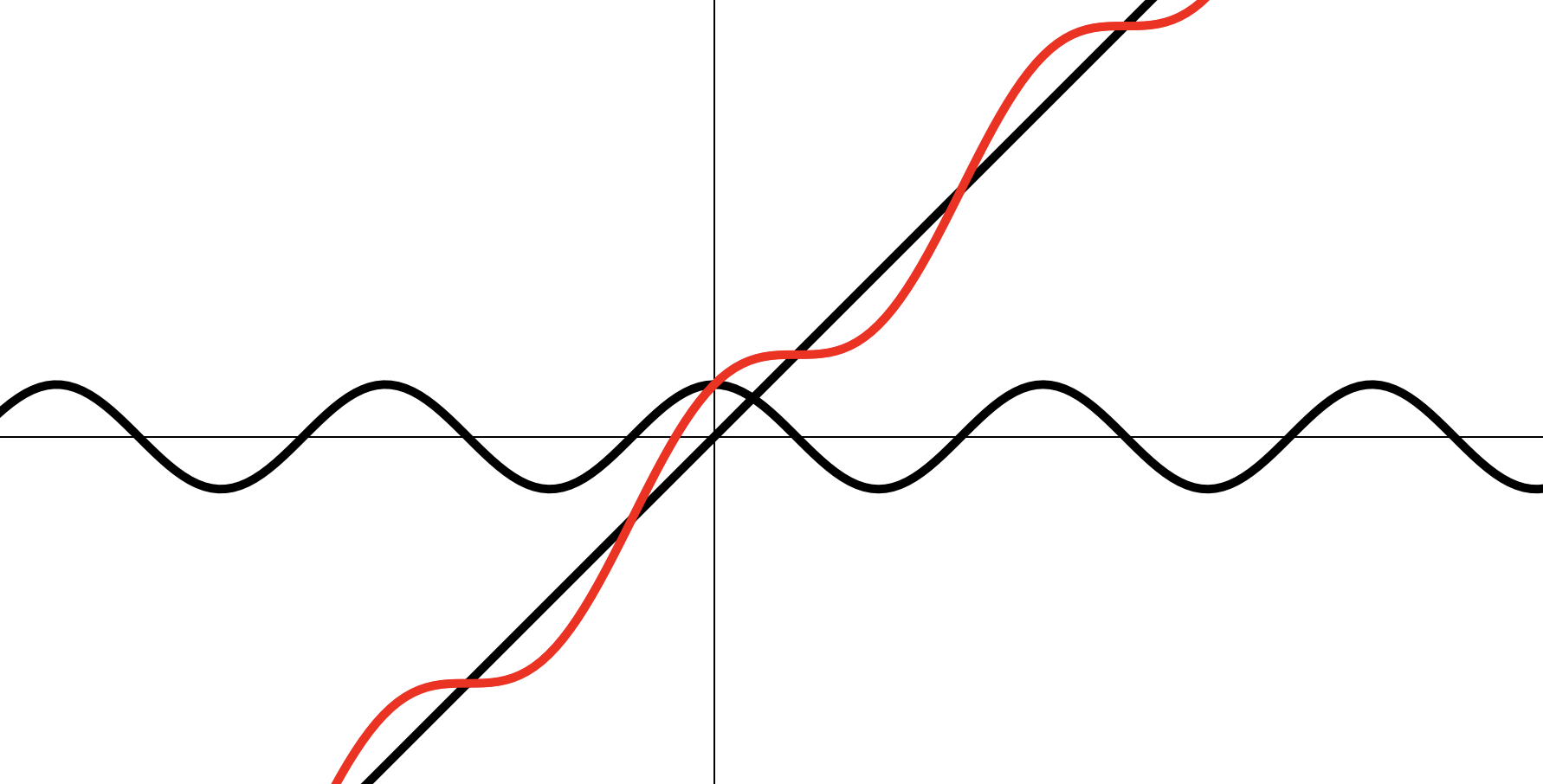
Пример 2
Построить эскиз графика
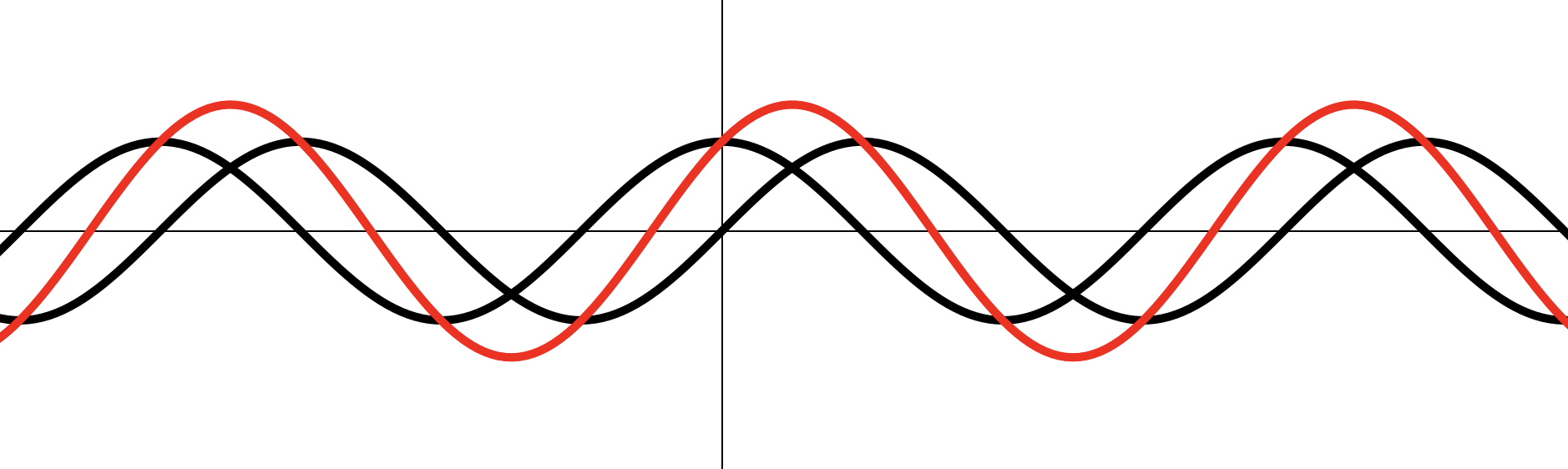
Еще примерчик ...
Построить эскиз графика
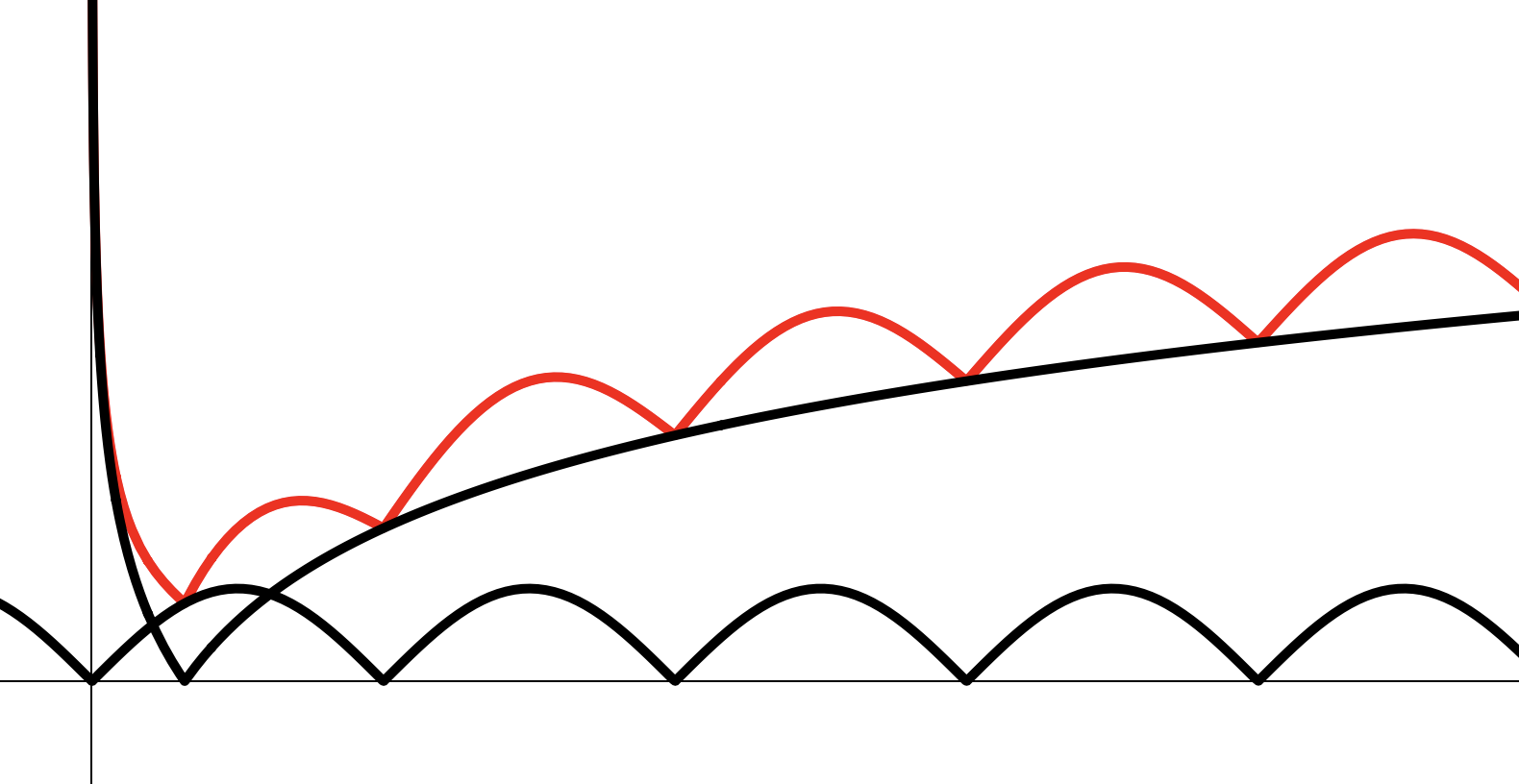
Построение графиков вида
Пример
Построить эскиз графика
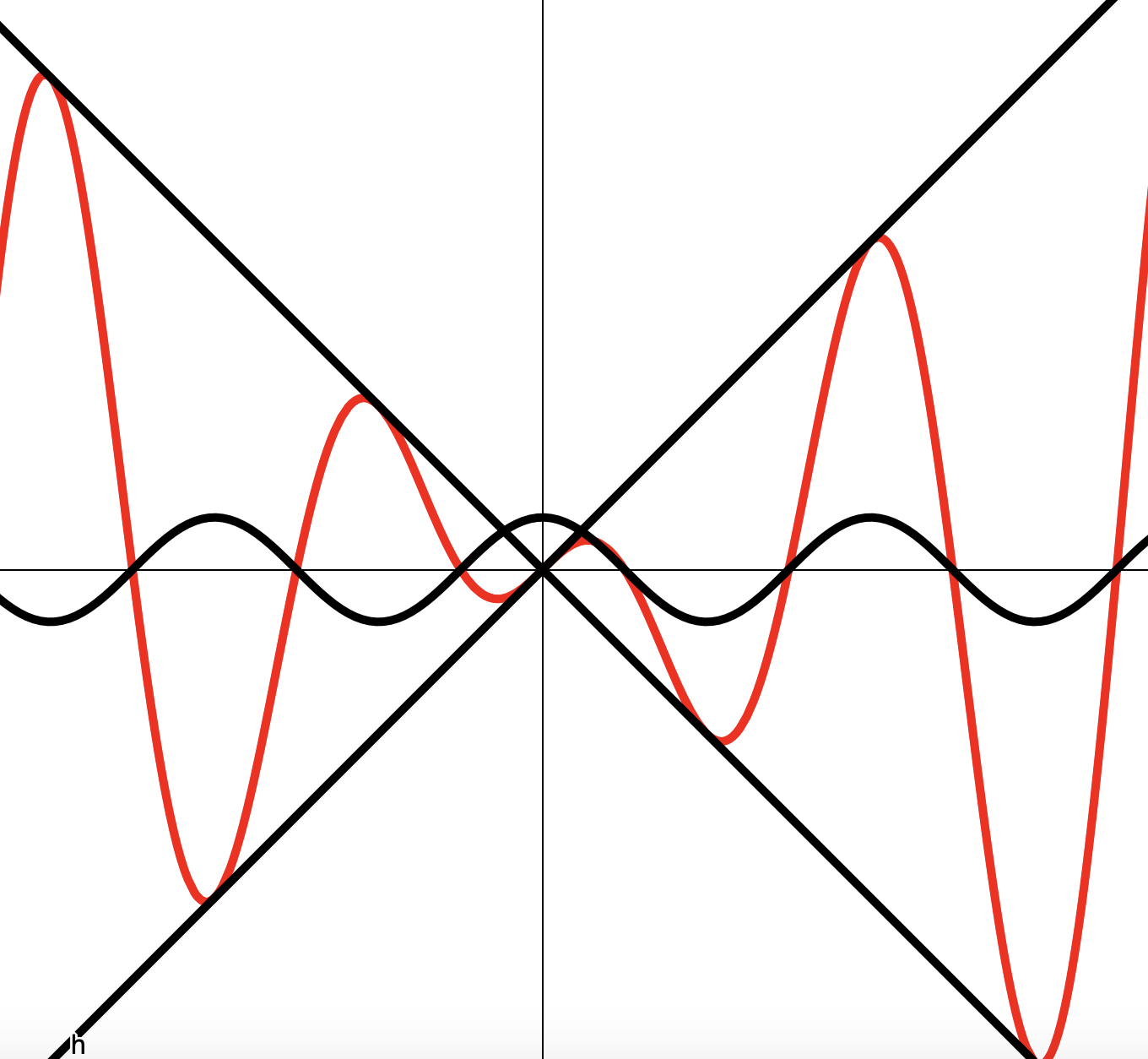
Построение графиков вида
Пример 1
Построить эскиз графика
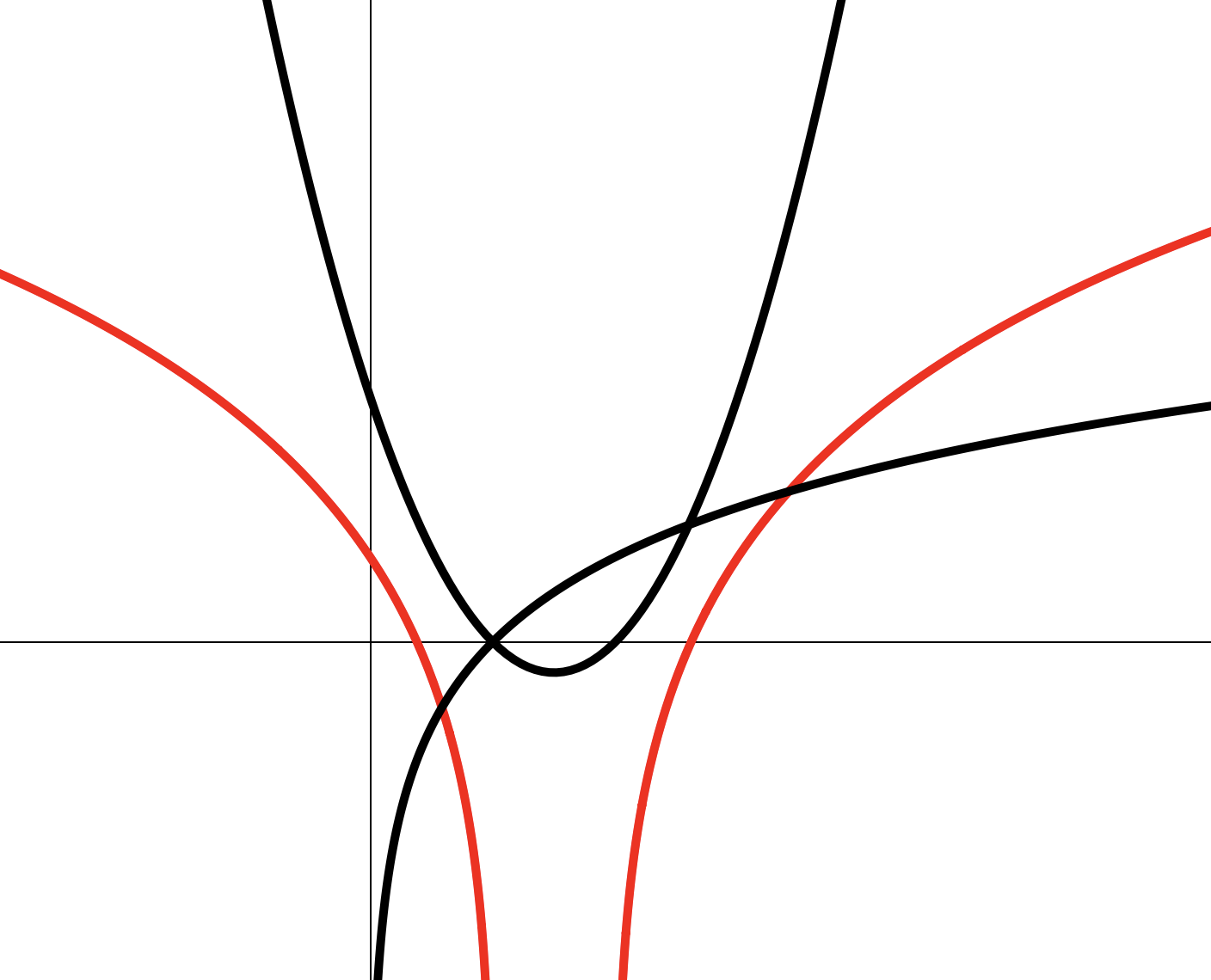
Пример 2
Построить эскиз графика
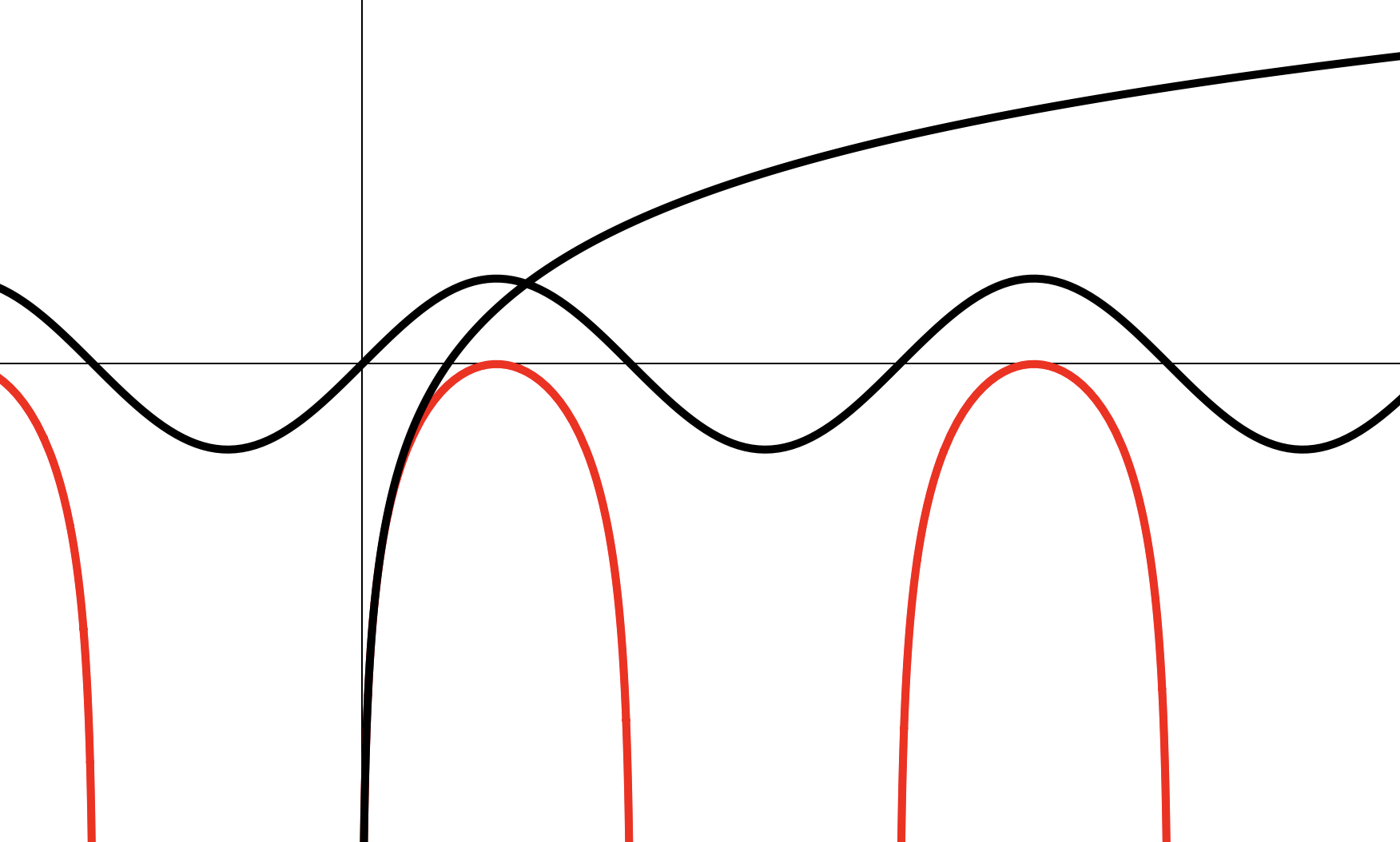
Задачи
Построить эскизы следующих функций:
А1. Элементарные функции. Элементарные преобразования графиков
By vkrysanov320
А1. Элементарные функции. Элементарные преобразования графиков
- 965



