Перпендикуляр и наклонные. Угол между прямой и плоскостью
10 класс
vkrysanov320@gmail.com
version 1.2, 08-11-2023
Расстояние от точки до плоскости
Расстояние от точки до плоскости — это длина перпендикуляра, опущенного из заданной точки к заданной плоскости.
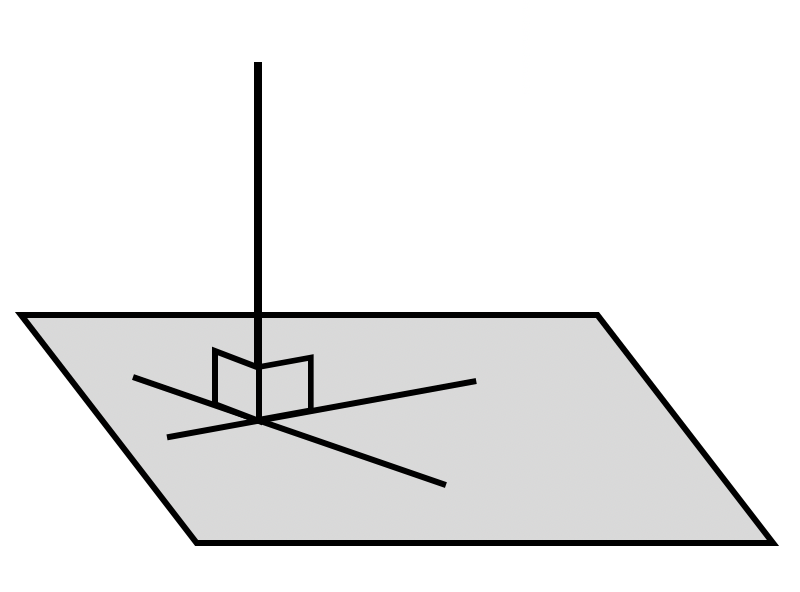
Раст-е от точки до плоскости. Замечание (1)
Если две плоскости параллельны, то все точки одной плоскости равноудалены от другой плоскости.
* Расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости называется расстоянием между параллельными плоскостями.
** Расстояние между плоскостями имеет место быть только для параллельных плоскостей.
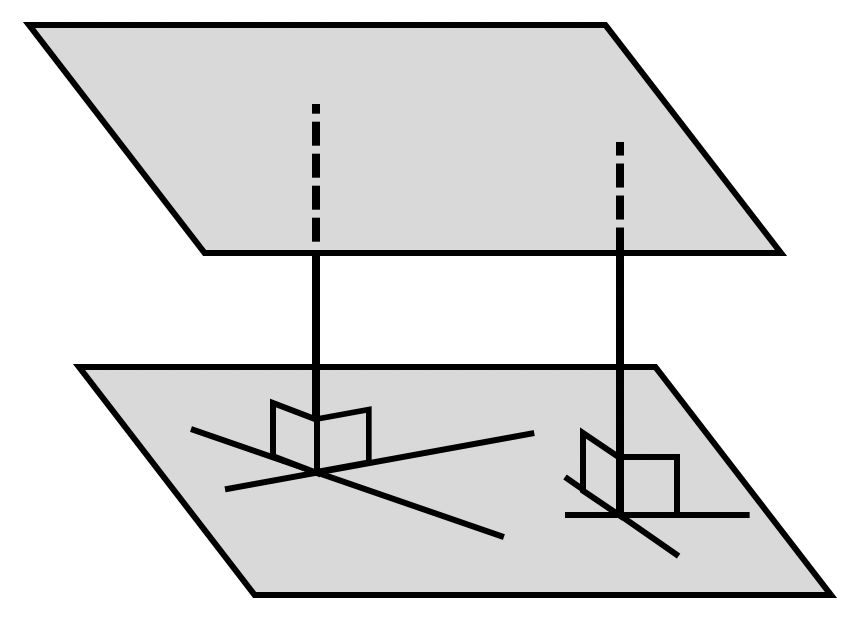
Раст-ие от точки до плоскости. Замечание (2)
Если прямая параллельна плоскости, то все точки прямой равноудалены от этой плоскости.
* B этом случае расстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью.
** Расстояние между прямой и плоскостью имеет место быть только для прямой, параллельной данной плоскости.
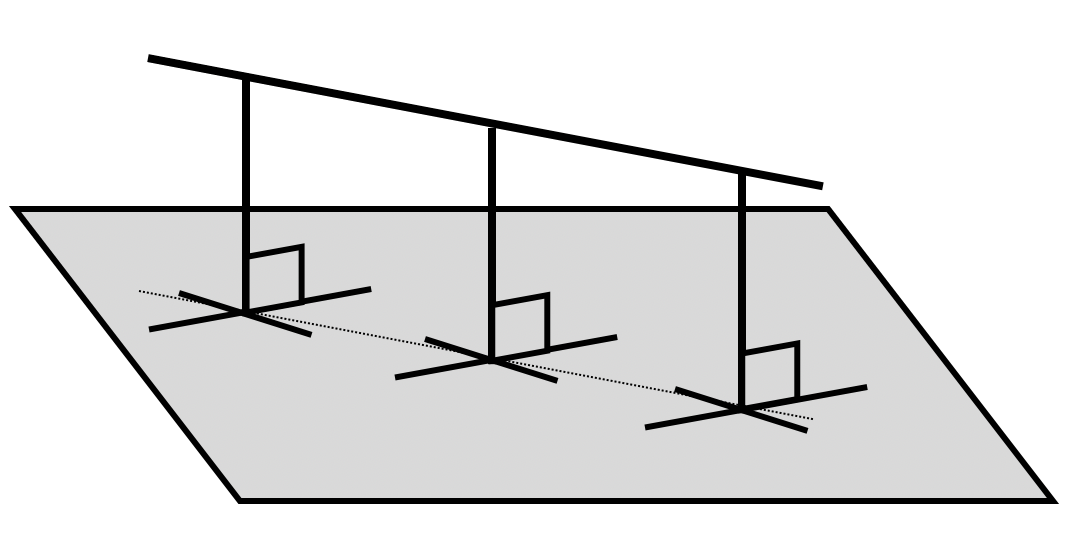
Раст-ие от точки до плоскости. Замечание (3)
Если две прямые скрещивающиеся, то, через каждую из них проходит плоскость, параллельная другой прямой, и притом только одна.
* Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.

Перпендикуляр, наклонная, проекция
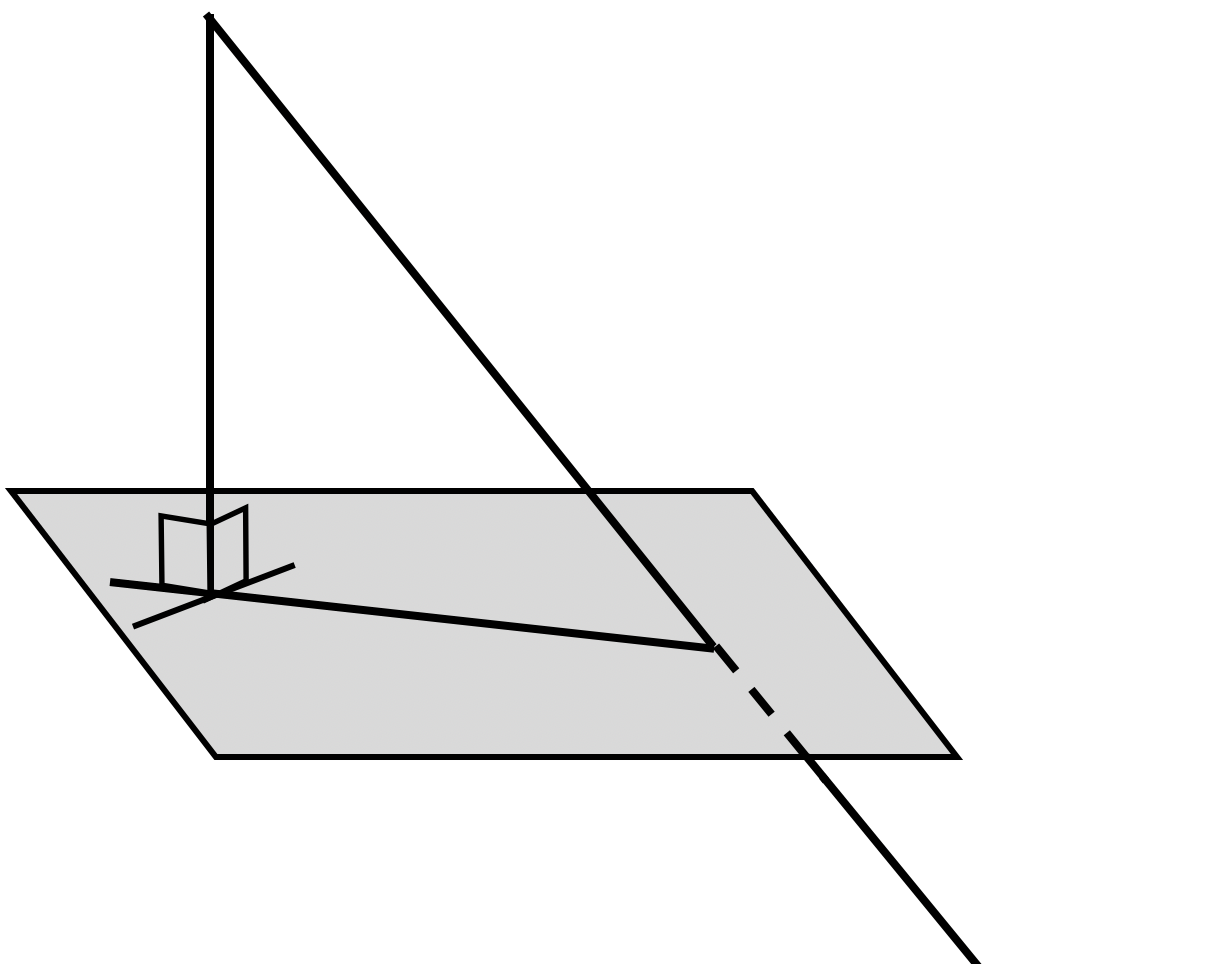
наклонная к плоскости
ортогональная проекция наклонной на плоскость
перпендикуляр из точки на плоскость
- Наклонной к плоскости называется такая прямая, которая пересекает эту плоскость и не перпендикулярна ей.
- Ортогональной проекцией точки на плоскость называют основание перпендикуляра, опущенного из этой точки на плоскость.
Задачи
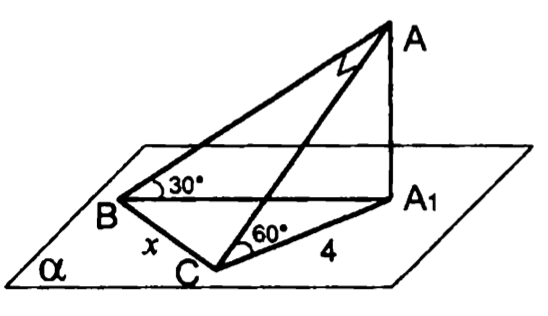
1.
— перпендикуляр к плоскости , и — наклонные. Найти .
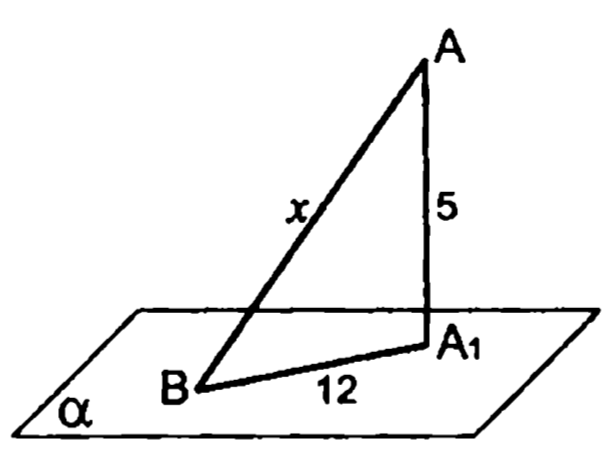
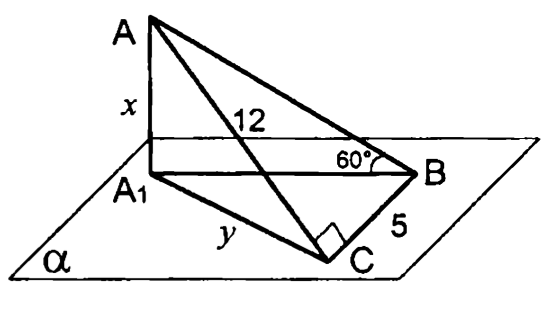
2.
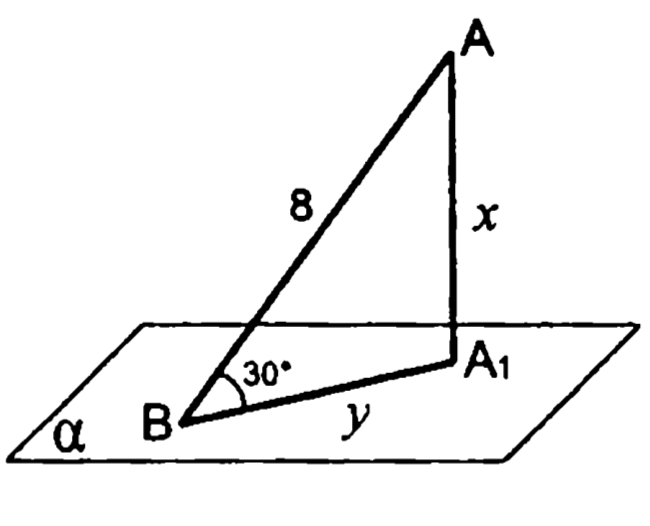
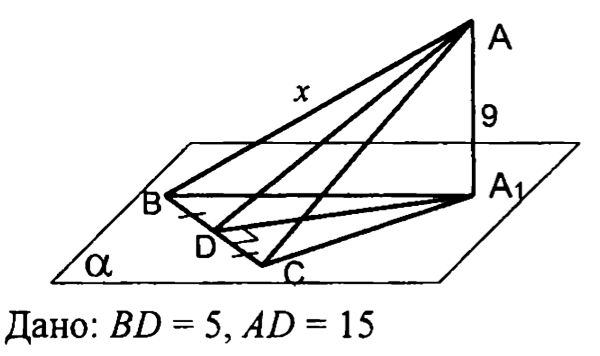
3.
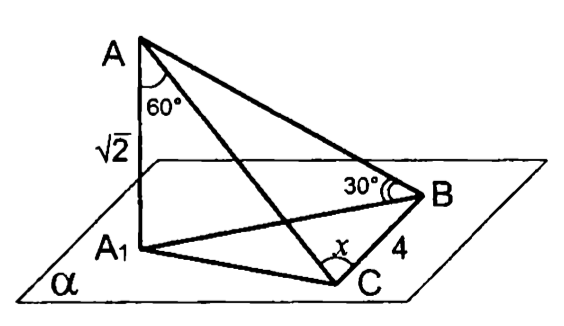
4.
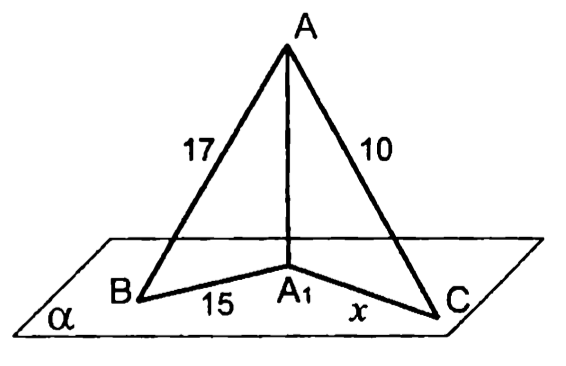
5.
6.
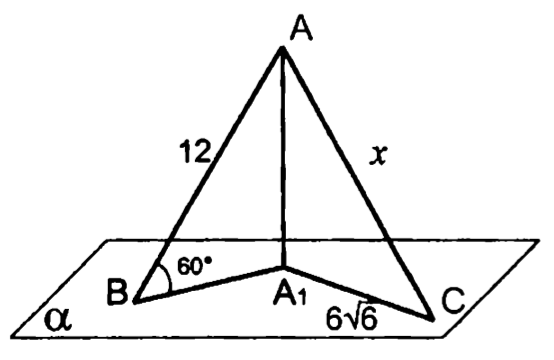
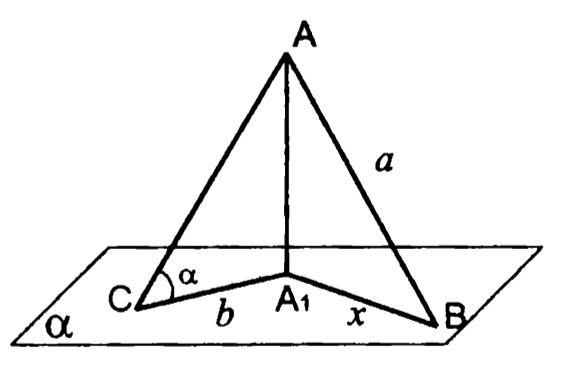
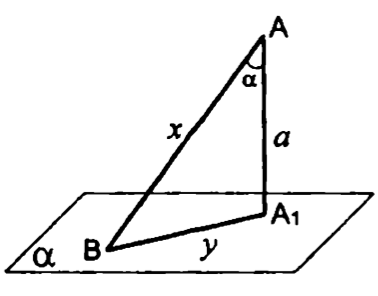
Задачи (2)
7.
— перпендикуляр к плоскости , и — наклонные. Найти .
8.
9.
10.
11.
12.
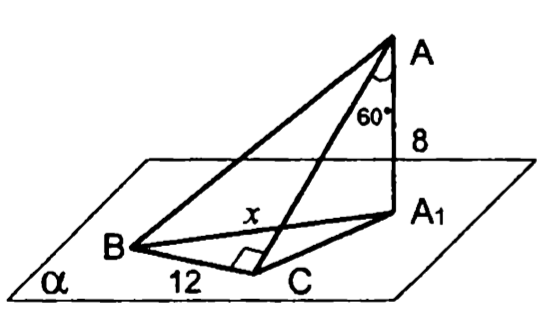
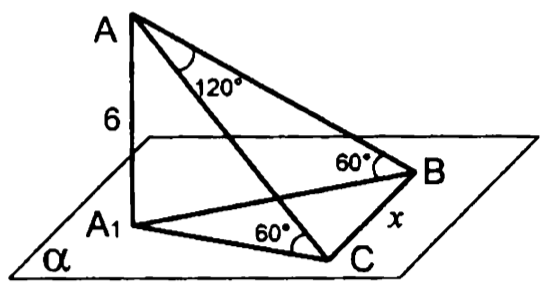

Свойство точки, равноудаленной от вершин многоугольника
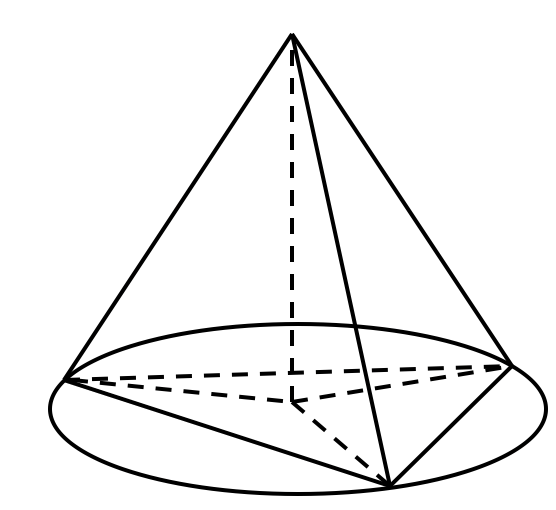
Если прямая, перпендикулярная плоскости многоугольника, проходит через центр описанной около многоугольника окружности, то каждая точка этой прямой равноудалена от вершин многоугольника.
— центр описанной окруж-ти у
Свойство точки, равноудаленной от вершин многоугольника (2)

Если точка, не лежащая в плоскости выпуклого многоугольника, равноудалена от вершин многоугольника, то основание перпендикуляра, проведенного из этой точки к плоскости, является центром окружности, описанной около многоугольника.
— центр описанной окружности у
Свойство точки, равноудаленной от сторон многоугольника
Если прямая, перпендикулярная плоскости многоугольника, проходит через центр вписанной в многоугольник окружности, то каждая точка этой прямой равноудалена от сторон многоугольника.
— центр вписанной окруж-ти в
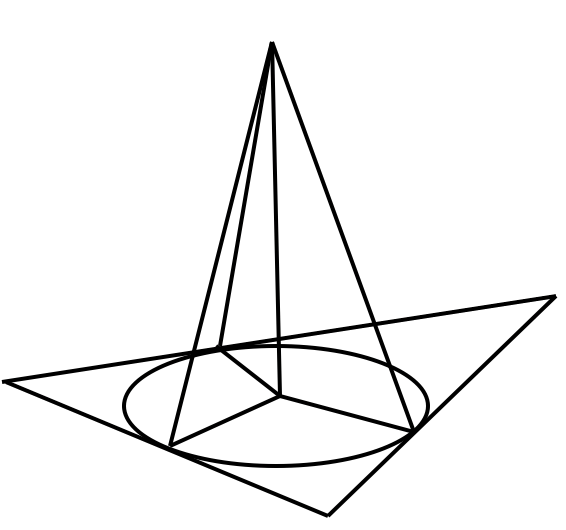
Свойство точки, равноудаленной от сторон многоугольника (2)
Если точка, не лежащая в плоскости выпуклого многоугольника, равноудалена от сторон многоугольника, то основание перпендикуляра, проведенного из этой точки к плоскости, является центром окружности, вписанной в многоугольник.
— центр вписанной окруж-ти в

Задачи
1. Расстояние от точки до вершин правильного треугольника равно 4. Найти расстояние от точки до плоскости , если
2. Расстояние от точки до каждой из сторон правильного треугольника равно 4. Найдите расстояние от точки до плоскости треугольника, если
Теорема о трёх перпендикулярах
Теорема: Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.
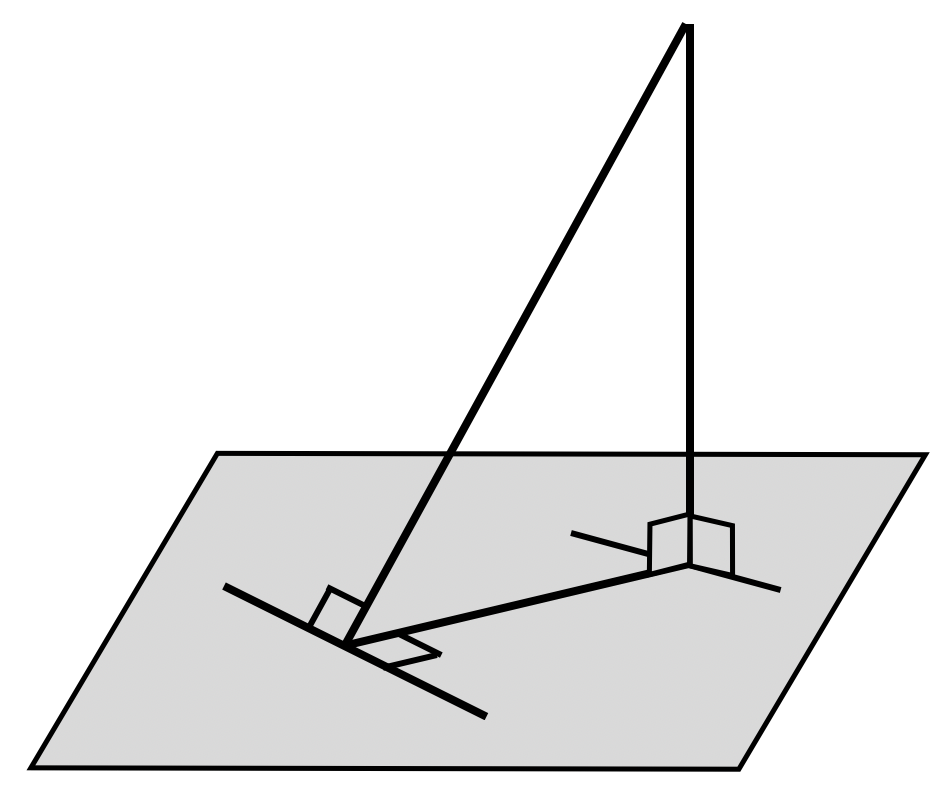
Обратная теорема: Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.
Задачи
1.
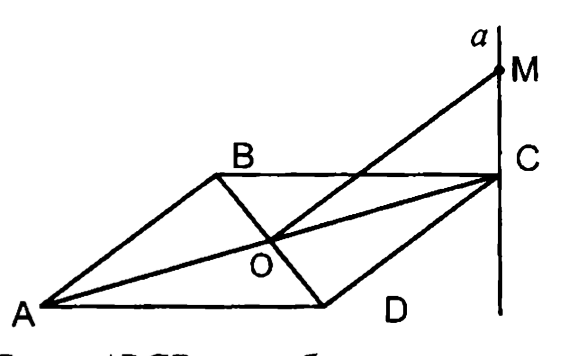
— ромб
т.д.
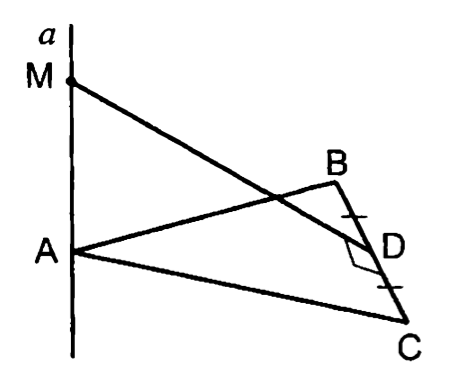
2.
т.д.

3.
— параллелограмм
т.д.
— прямоугольник
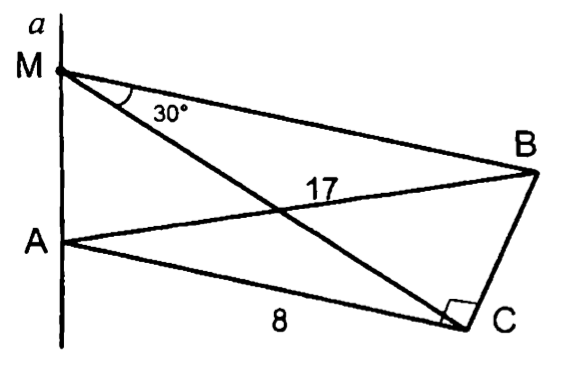
3.
4.
т.н.
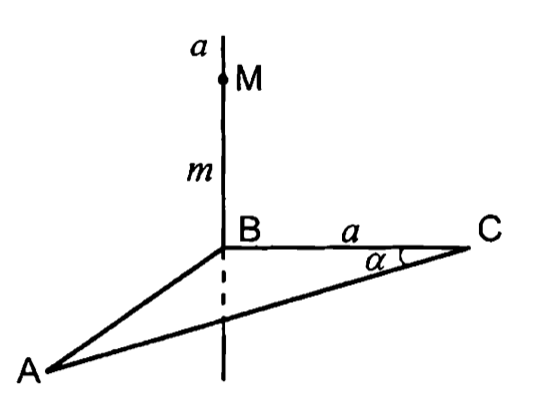
5.
т.н.
Задачи (2)
6.
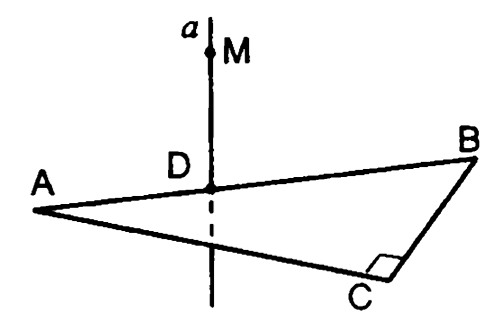
Построить перпендикуляры из точки к прямым и
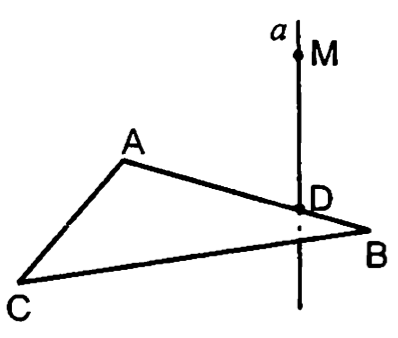
7.
— правильный
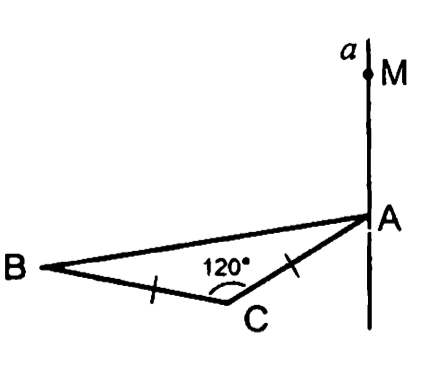
Построить перпендикуляры из точки к прямым и
8.
Построить перпендикуляр из точки к прямой
Задачи (3)
9.
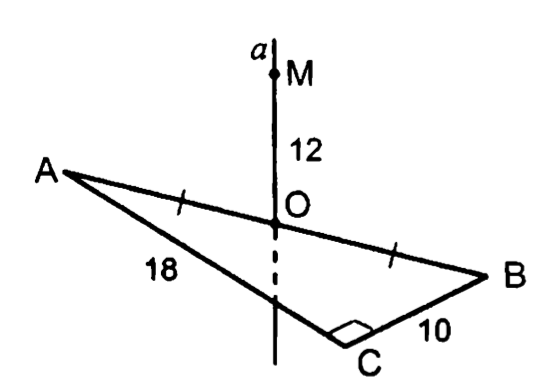
т.н.
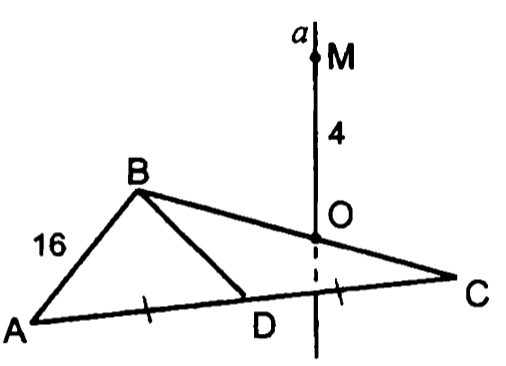
10.
— правильный
т.н.
11.
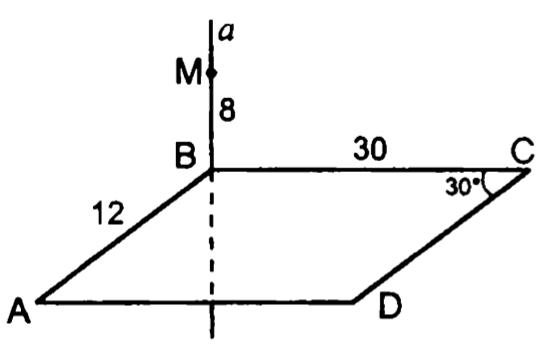
— параллелограмм
т.н.
Задачи (4)
12.
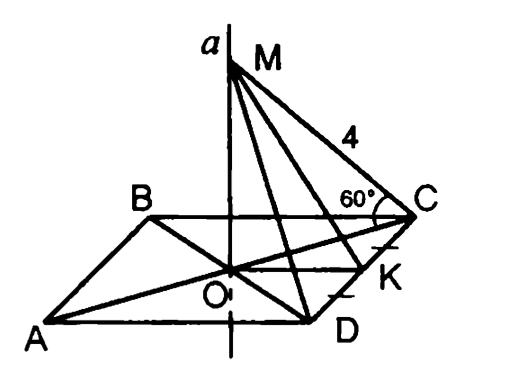
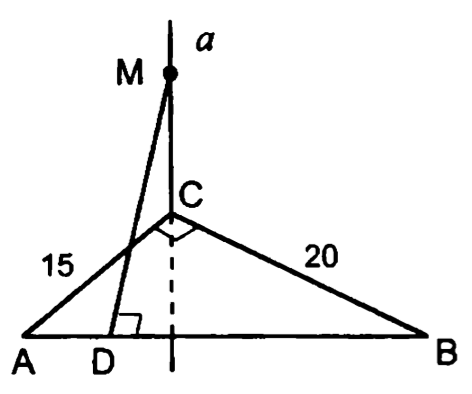
13.
— квадрат
т.н.
т.н.
Задачи (5)
14.
15.
т.н.
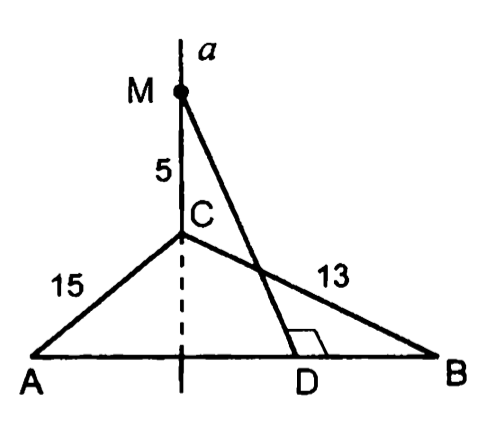
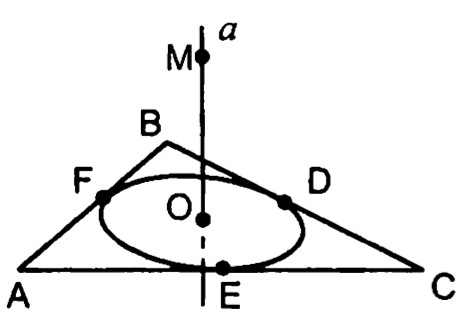
— правильный
— центр окружности,
вписанный в
т.н.
Угол между прямой и плоскостью
Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.
* Угол между плоскостью и параллельной ей прямой равен .
** Угол между плоскостью и перпендикулярной ей прямой равен .
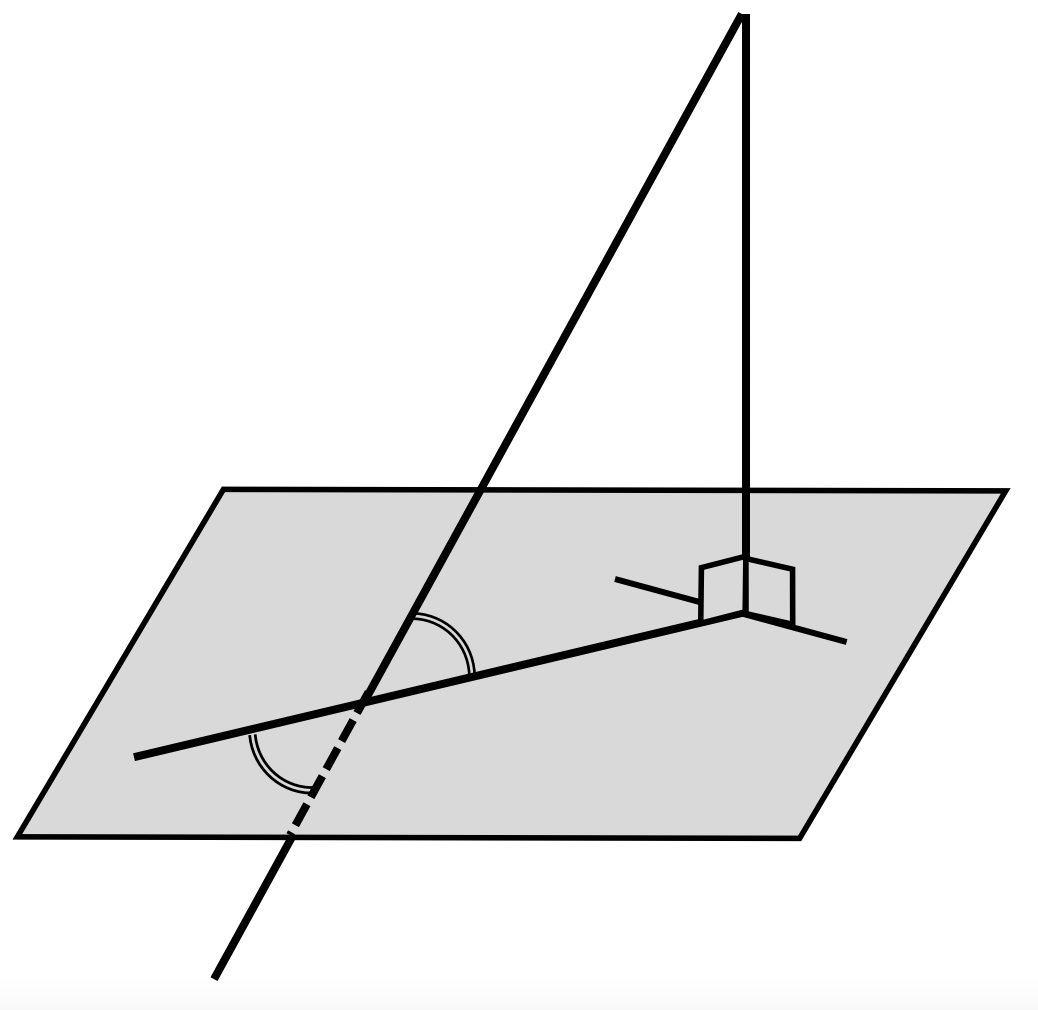
— проекция на плоскость
т.к.
Задачи
2. В кубе найти угол между прямой и плоскостью .
1. В правильном тетраэдре найти угол между боковым ребром и плоскостью основания.
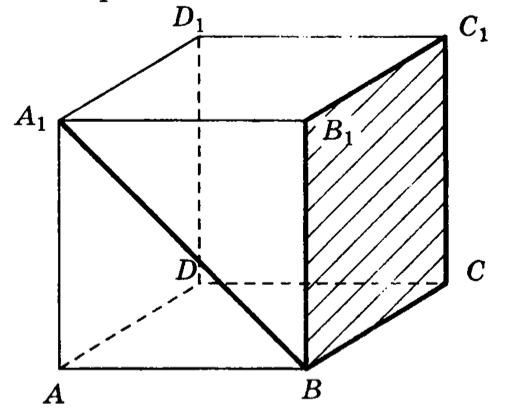
3. В кубе найти угол между прямой и плоскостью .
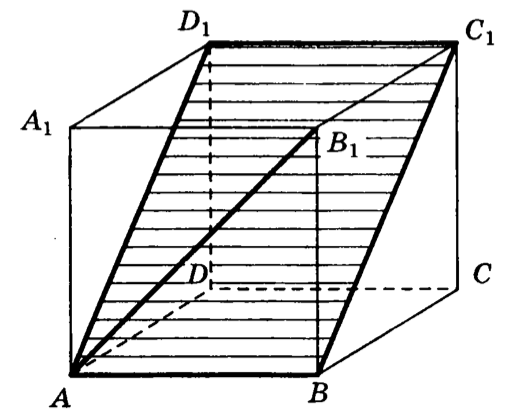
4. В кубе найти угол между прямой и плоскостью .
5. В кубе найти угол между прямой и плоскостью .
6. В кубе найти угол между прямой и плоскостью .
Задачи (2)
7. В правильном треугольной призме , все ребра которой равны 1, найти угол между прямой и плоскостью .
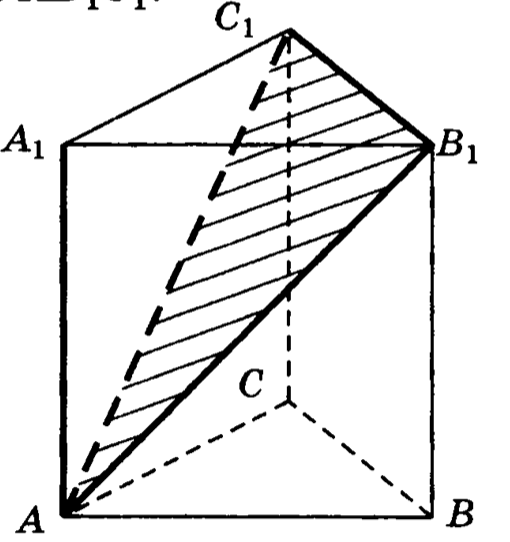
8. В правильном треугольной призме , все ребра которой равны 1, найти угол между прямой и плоскостью .
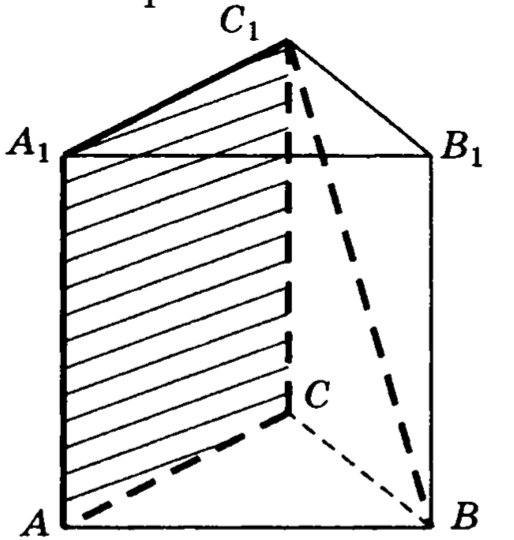
9. В правильном треугольной призме , все ребра которой равны 1, найти угол между прямой и плоскостью .
10. В правильном треугольной призме , все ребра которой равны 1, найти угол между прямой и плоскостью .
Задачи (3)
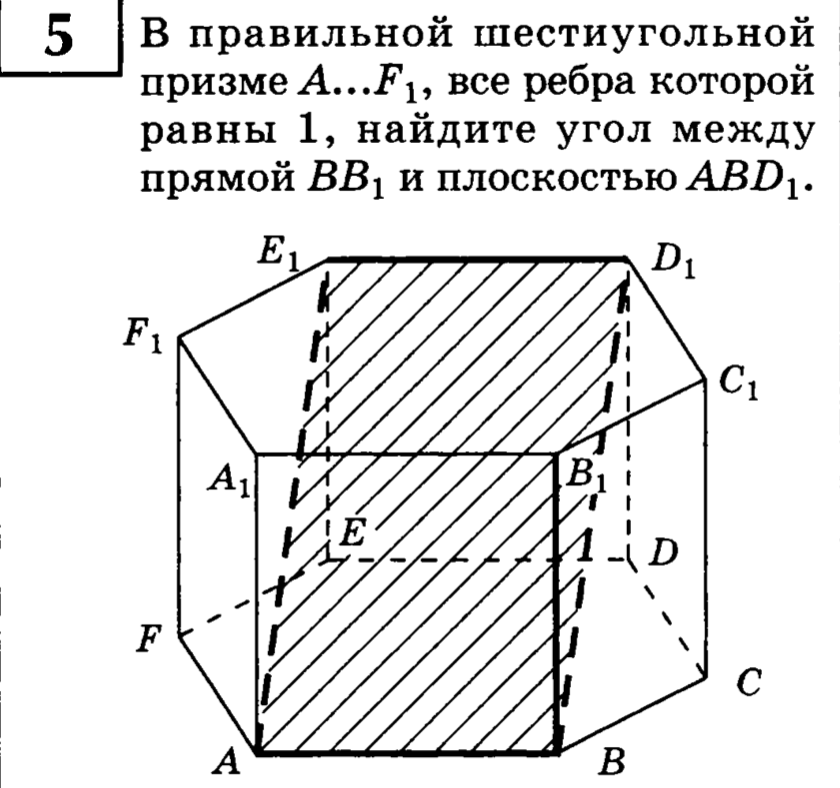
11. В правильном шестиугольной призме , все ребра которой равны 1, найти угол между прямой и плоскостью .
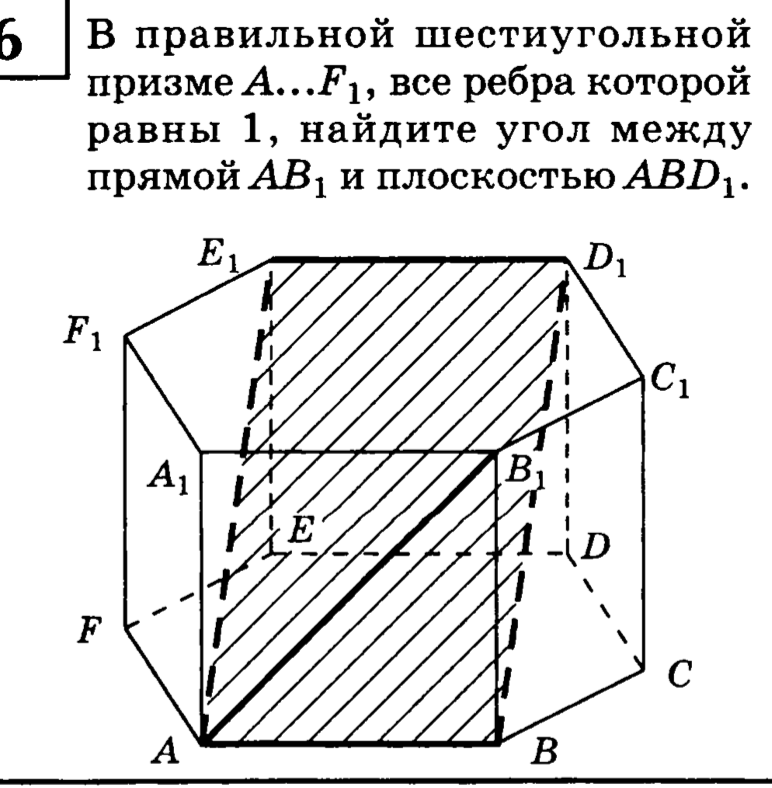
12. В правильном шестиугольной призме , все ребра которой равны 1, найти угол между прямой и плоскостью .
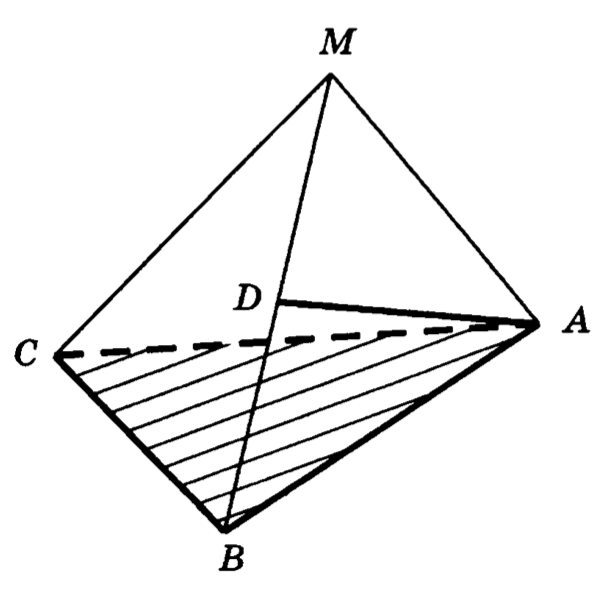
13. В правильном тетраэдре , все ребра которого равны 1, найти угол между апофемой и плоскостью .
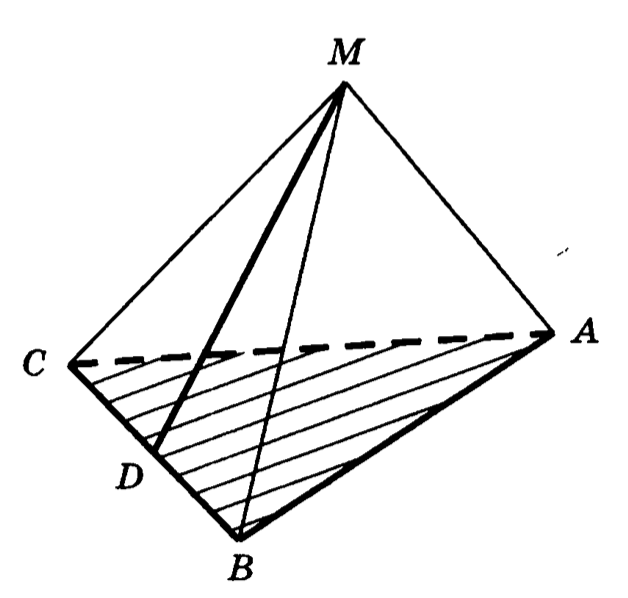
14. В правильном тетраэдре , все ребра которого равны 1, точка — середина . Найти угол между прямой и плоскостью
Задачи (на дом)
16. В правильном треугольной призме , все ребра которой равны 1, найти угол между прямой и плоскостью .

15. В кубе найти угол между прямой и плоскостью .
17. В правильном шестиугольной призме , все ребра которой равны 1, найти угол между прямой и плоскостью .
18. В правильном четырехугольной пирамиде , все ребра которой равны 1, найти угол между прямой и плоскостью , где — середина .
Двугранный угол. Угол между плоскостями.
Перпендикулярность плоскостей
Двугранный угол
Двугранным углом называется фигура, образованная прямой и двумя полуплоскостями с общей границей , не принадлежащими одной плоскости.
Величина двугранного угла
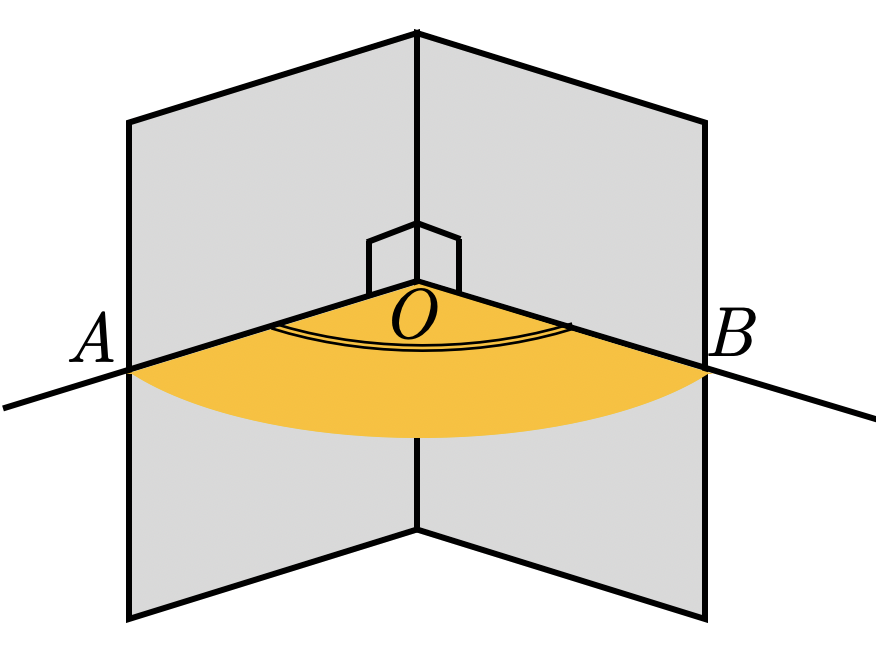
Величиной двугранного угла называется величина его линейного угла.
Величина двугранного угла, измеренная в градусах, принадлежит промежутку от до .
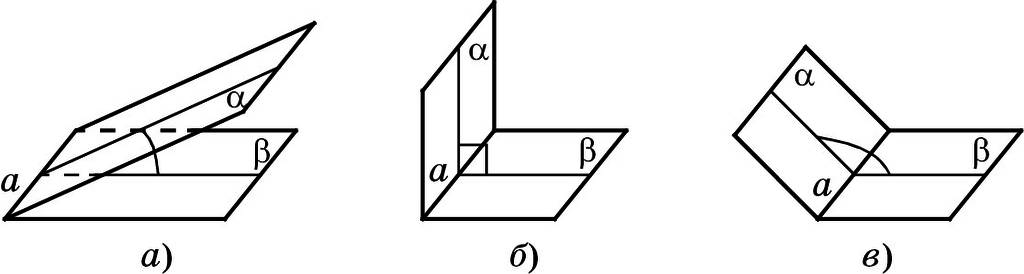
Виды двугранных углов:


острый
прямой
тупой
Величина двугранного угла (2)
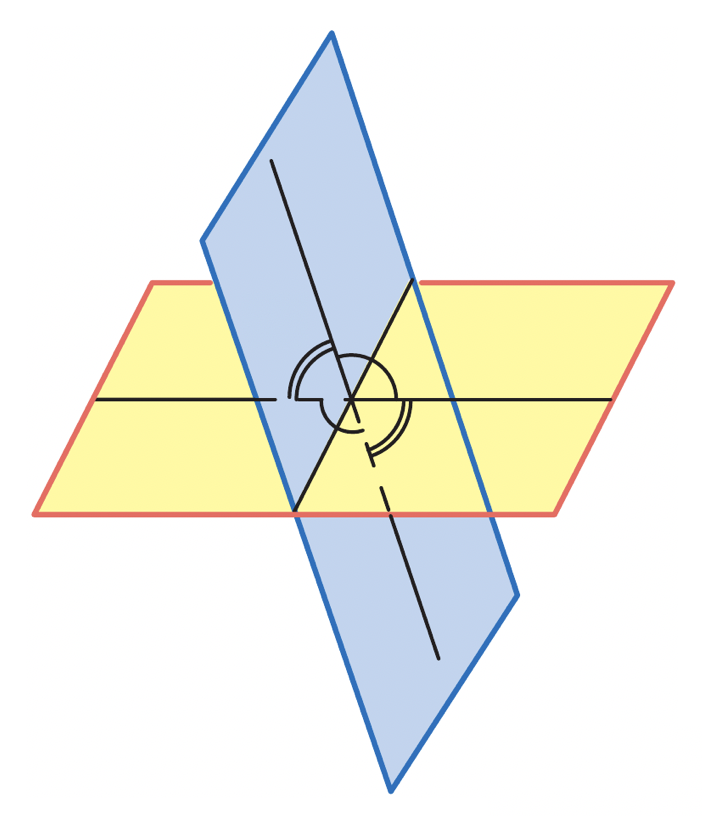
Если в пространстве пересекаются две плоскости, получаются четыре двугранных угла (аналогично как при пересечении двух прямых получаются четыре угла).
тупые:
острые:
* или же прямые, если плоскости перпендикулярны
Теорема: Величина линейного угла не зависит от выбора его вершины на ребре двугранного угла.
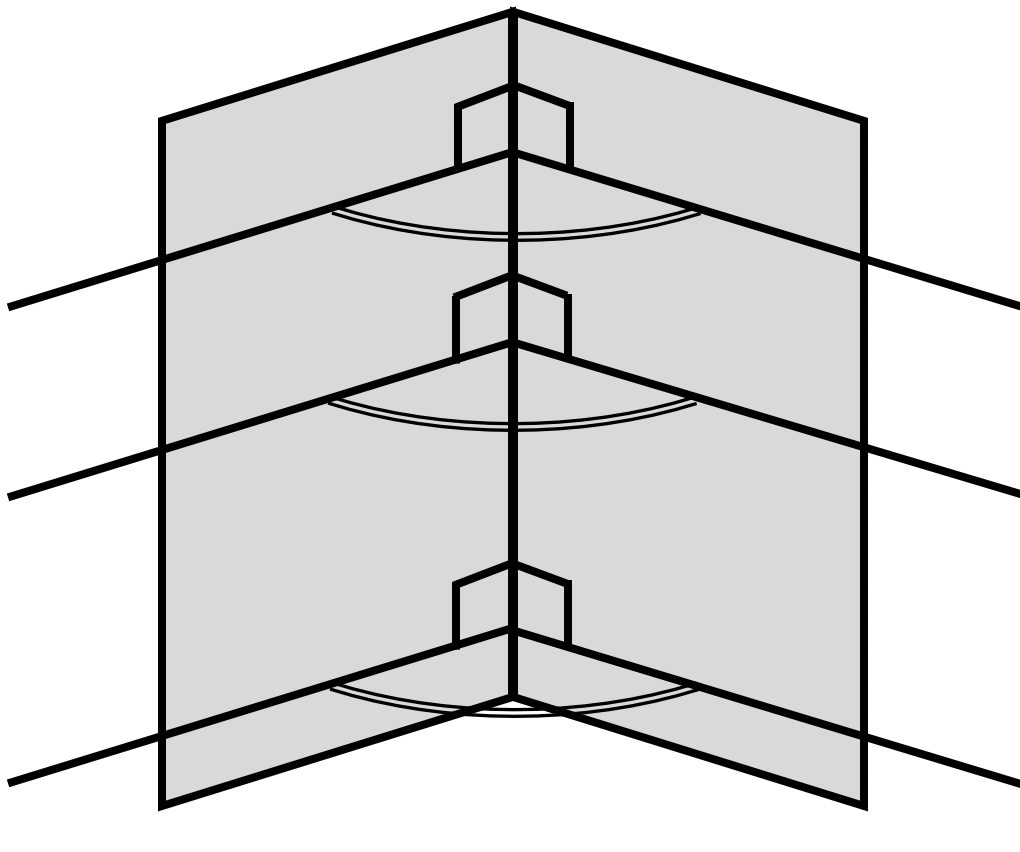
Величина двугранного угла (3)
Теорема: Величина линейного угла не зависит от выбора его вершины на ребре двугранного угла.
Угол между плоскостями
Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов, образованных при их пересечении.

* или же вертикальный ему угол.
Величина угла между плоскостями, измеренная в градусах, принадлежит промежутку от до .
Нахождение угла между плоскостями
Метод перпендикуляров к плоскостям *
Метод перпендикуляров к линии пересечения плоскостей
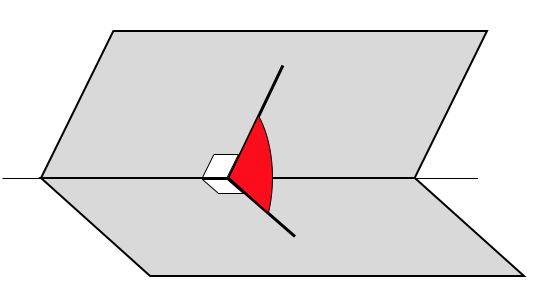
*полагается острый угол (или прямой)
Угол между плоскостями вычисляется как угол между перпендикулярами к данным плоскостям.
Угол между плоскостями вычисляется как угол между прямыми, лежащими в этих плоскостях и перпендикулярными к линии их пересечения.
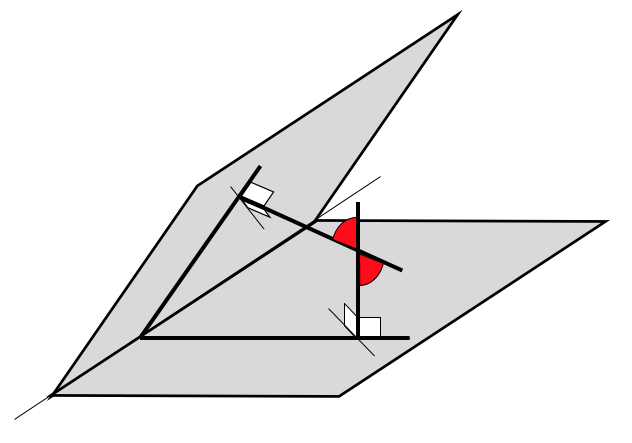
в данном случае тупой
Перпендикулярность плоскостей
Две плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен .
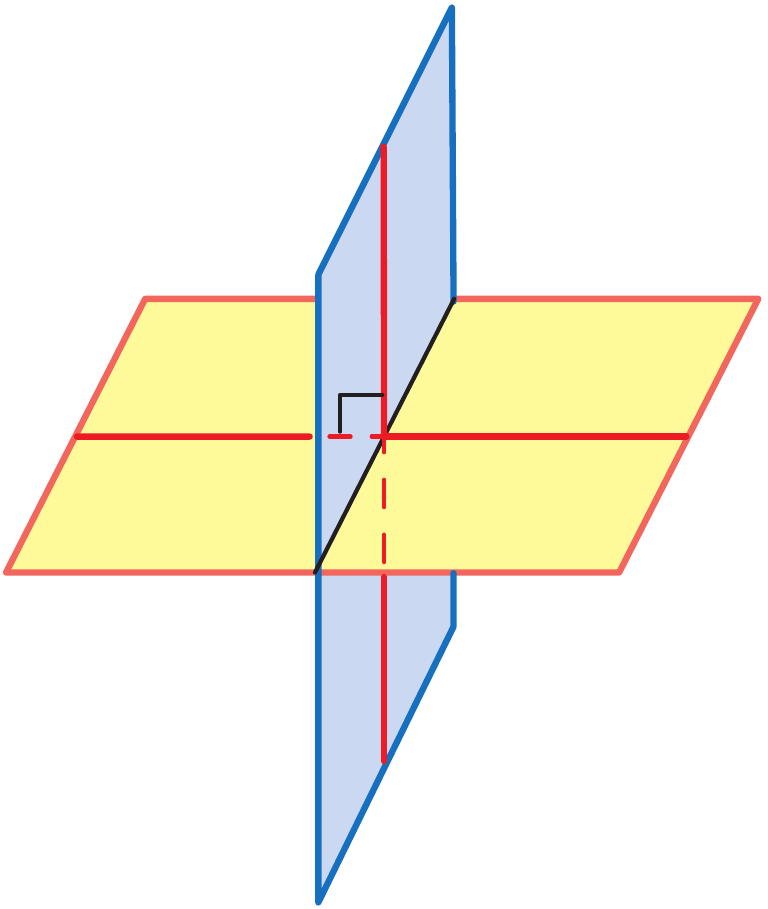
Теорема: Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
Следствие: Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.
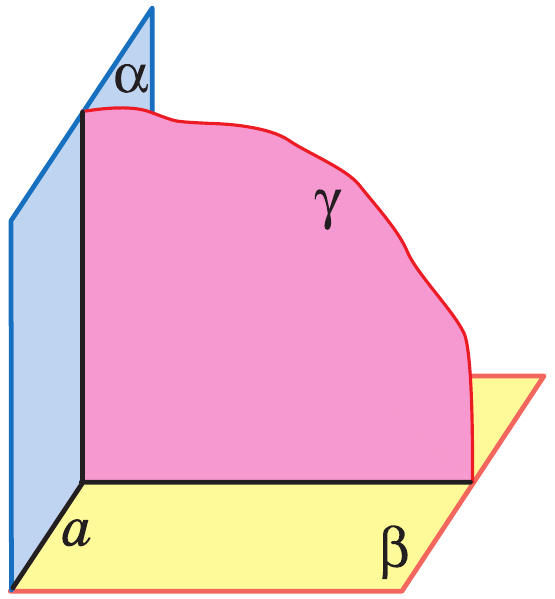
Задачи
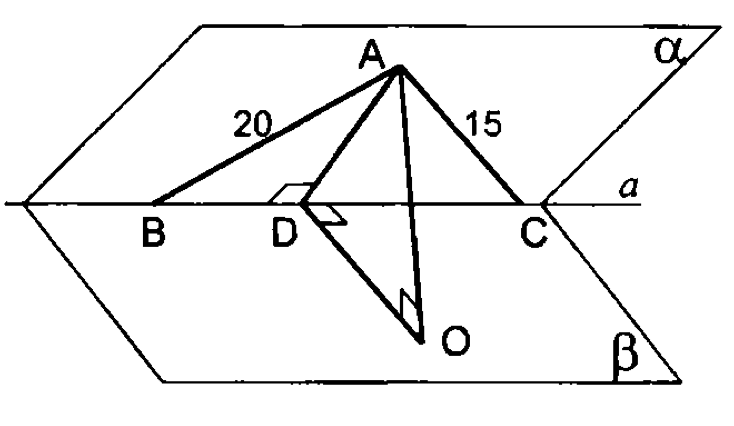
1.
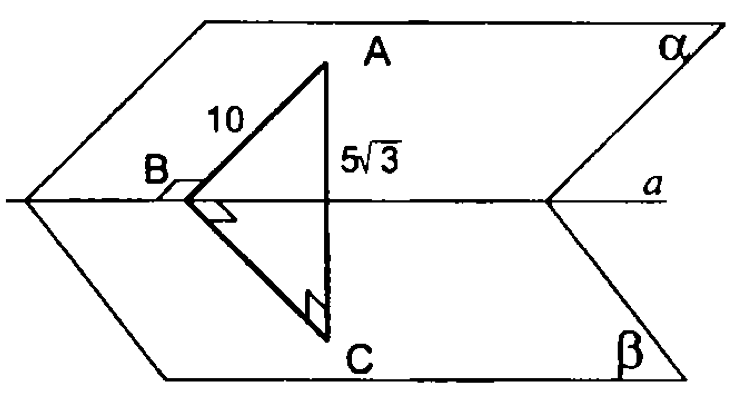
Известно, что . Для каждой задачи требуется найти или выразить его через любую тригонометрическую функцию:
2.
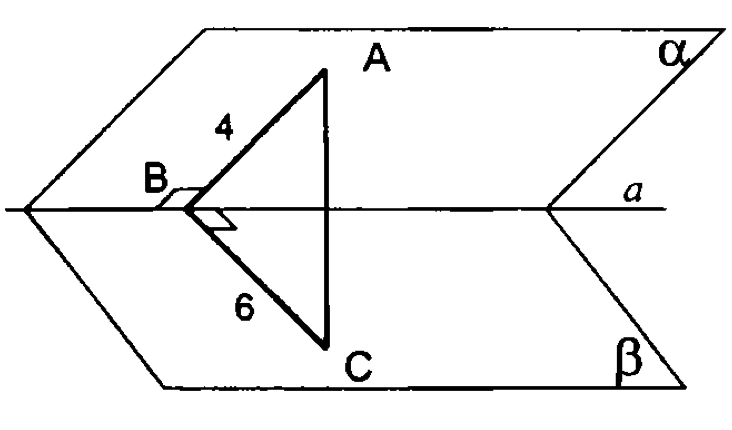
3.
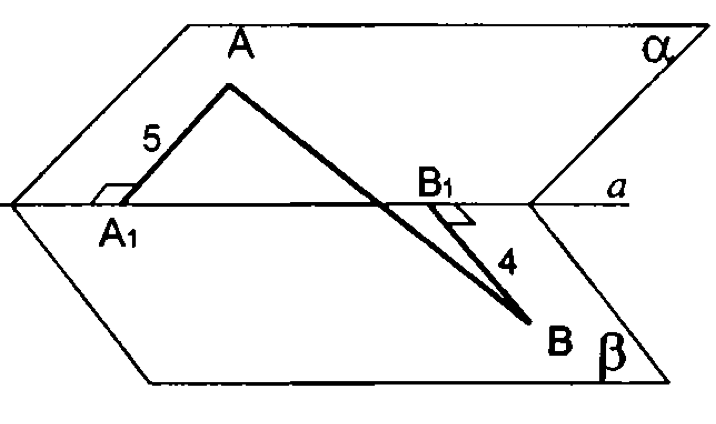
4.
Задачи (2)
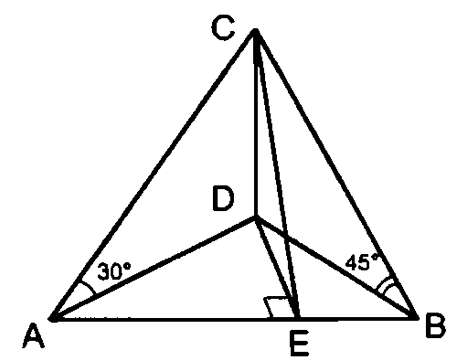
5.
т.н.
(или выразить угол через любую тригонометрическую функцию)
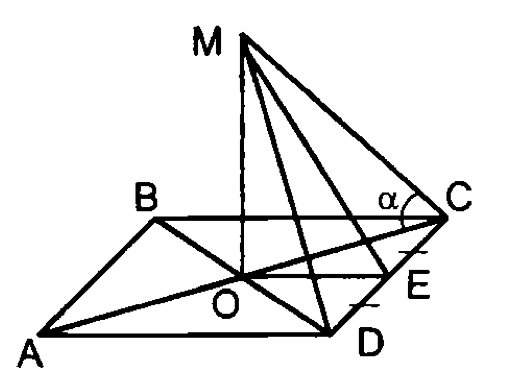
6.
квадрат;
т.н.
(или выразить угол через любую тригонометрическую функцию)
Задачи (3)
7.
т.д.
8.
т.д.
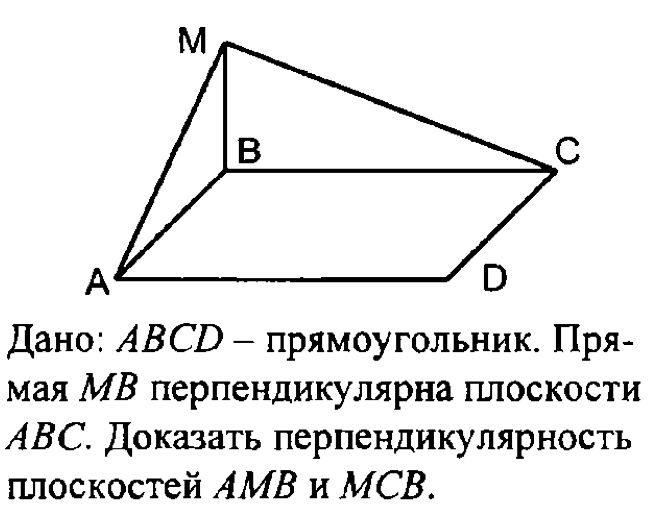
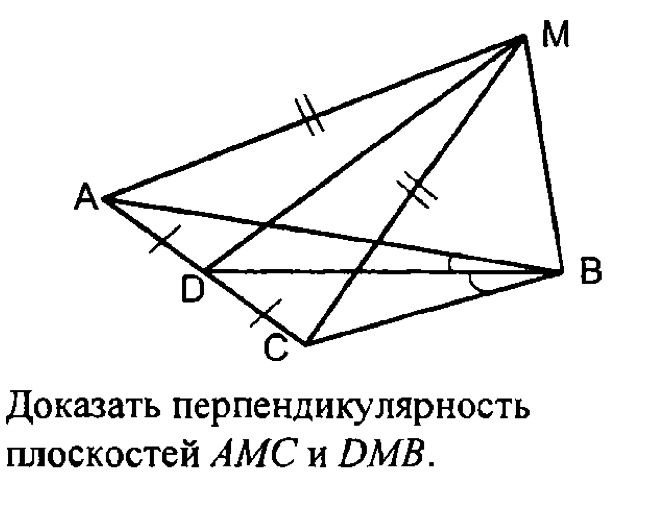
прямоугольник;

10.
квадрат
т.д. а)
б)
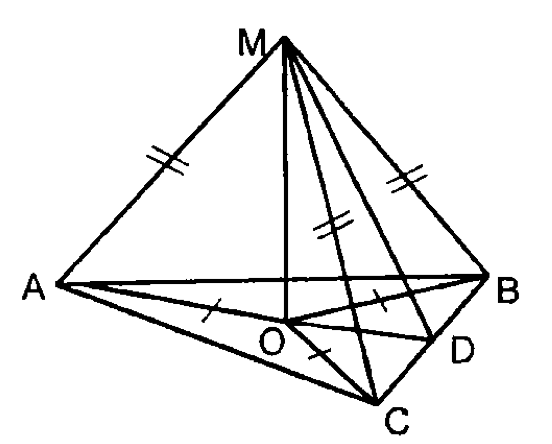
т.д. а)
т.д.
9.
Задачи (4)
11.
т.н.
прямоугольник;
прямоугольник;
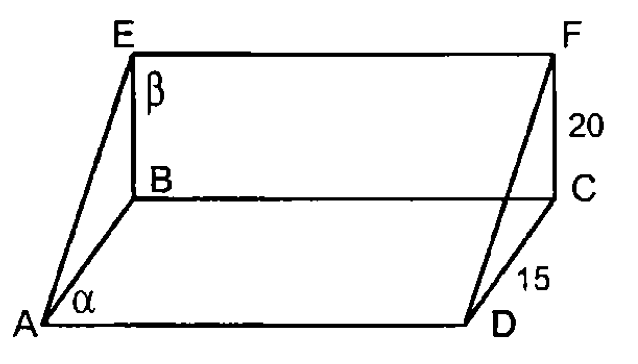
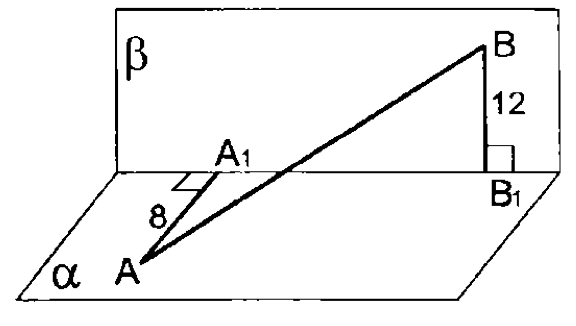
12.
т.н.
13. В кубе найти
14. Найдите угол между двумя гранями правильного тетраэдра.
Задачи (5)
15. В кубе найти угол между плоскостями и
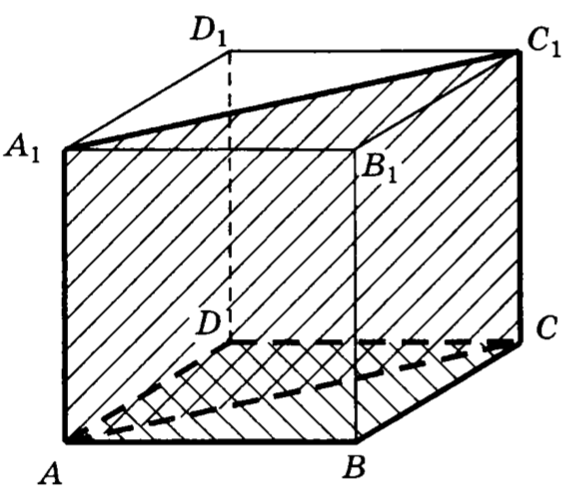
16. В кубе найти угол между плоскостями и .
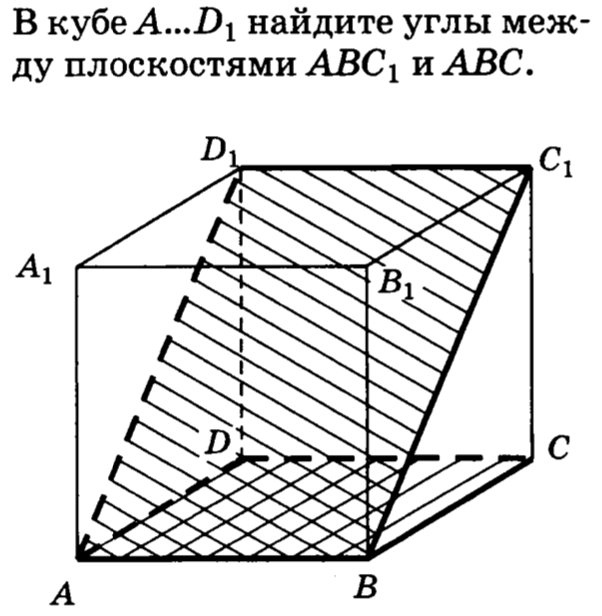
17. В кубе найти угол между плоскостями и .
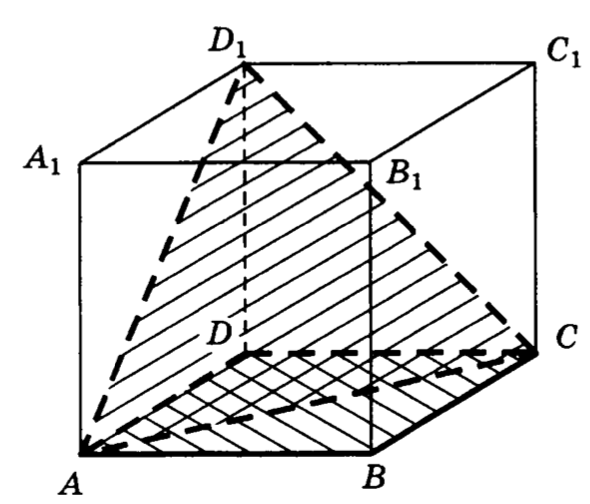
18. В кубе найти угол между плоскостями и .
Задачи (6)
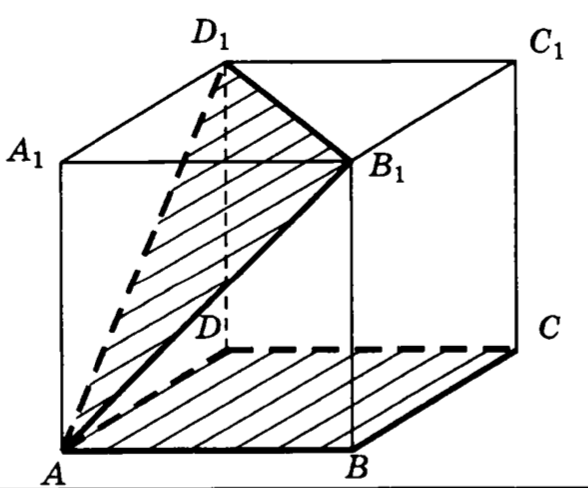
19. В кубе найти угол между плоскостями и
20. В кубе найти угол между плоскостями и .
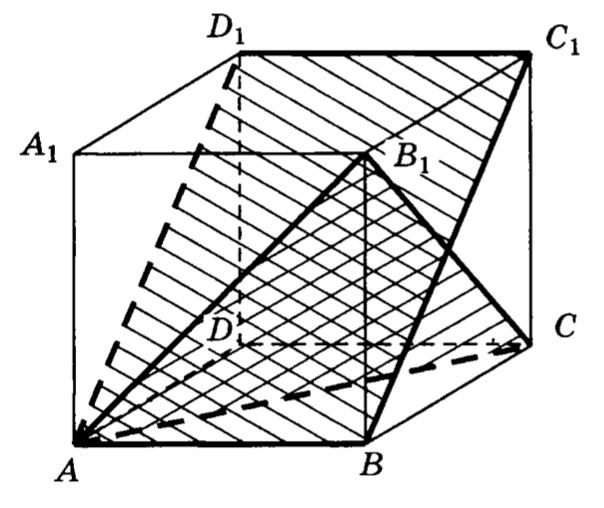
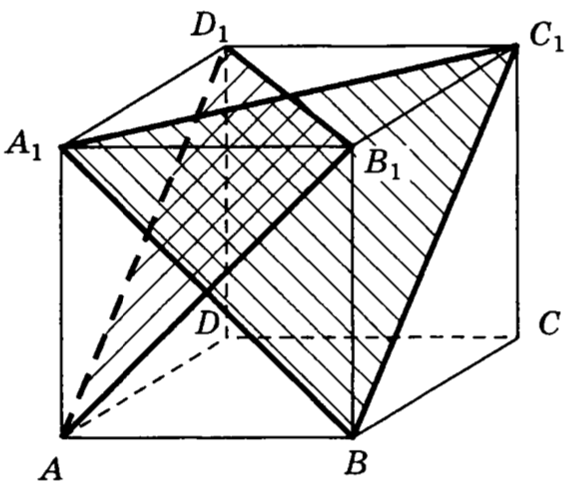
21. В правильной треугольной призме все ребра которой равны , найти угол между плоскостями и .
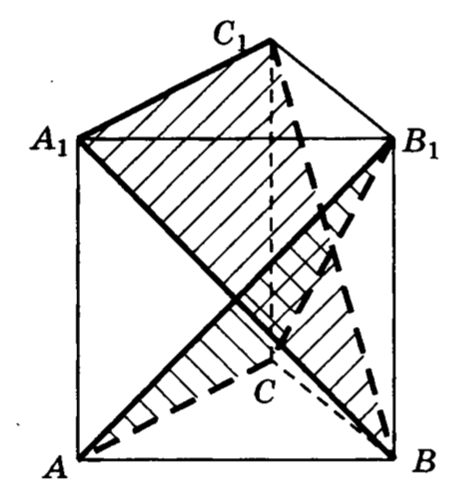
Задачи (7)
22. В правильной треугольной призме все ребра которой равны , найти угол между плоскостями и .
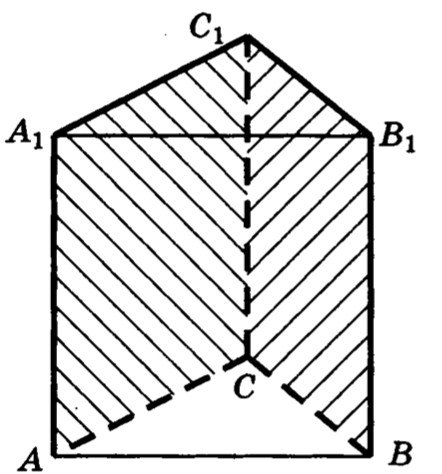
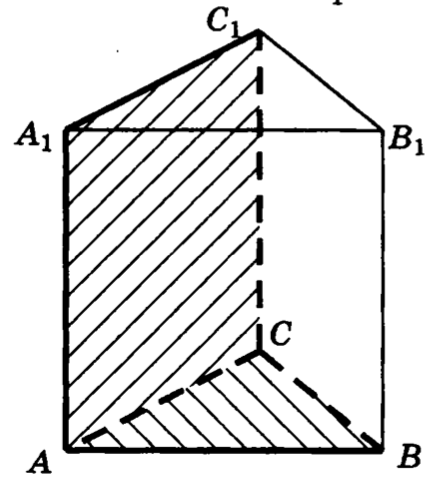
23. В правильной треугольной призме все ребра которой равны , найти угол между плоскостями и .
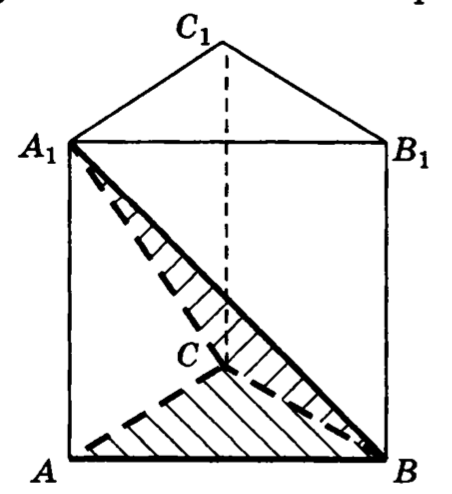
24. В правильной треугольной призме все ребра которой равны , найти угол между плоскостями и .
Задачи (8)
25. В правильной шестиугольной призме все ребра которой равны , найти угол между плоскостями и .
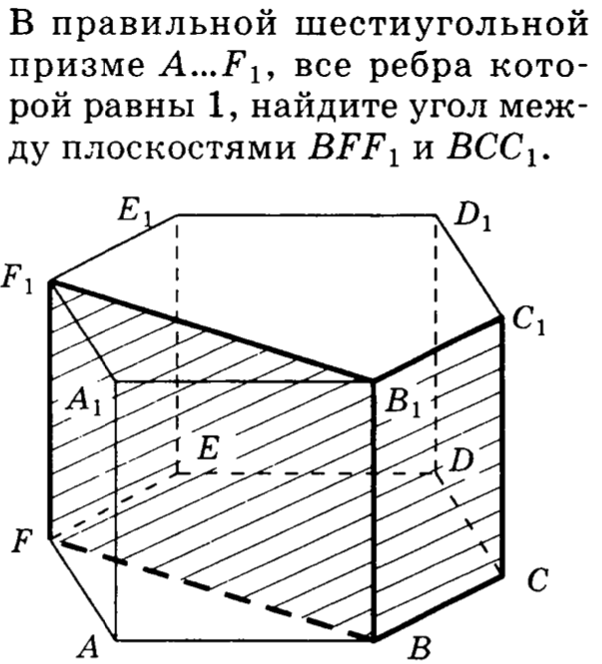
26. В правильной шестиугольной призме все ребра которой равны , найти угол между плоскостями и .
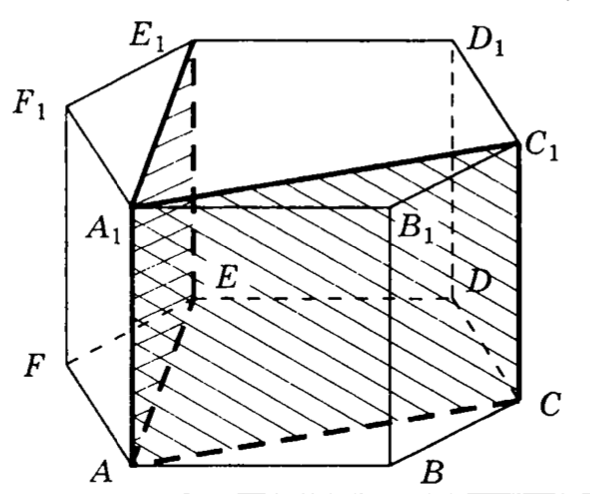
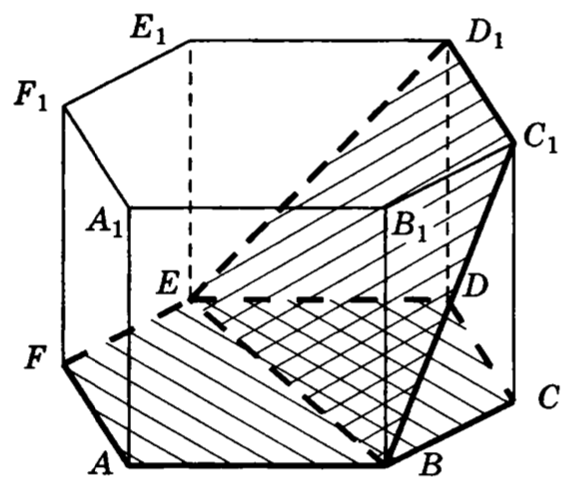
27. В правильной шестиугольной призме все ребра которой равны , найти угол между плоскостями и .
Задачи (9)
28. В правильной четырехугольной пирамиде все ребра которой равны , найти угол между плоскостями и .
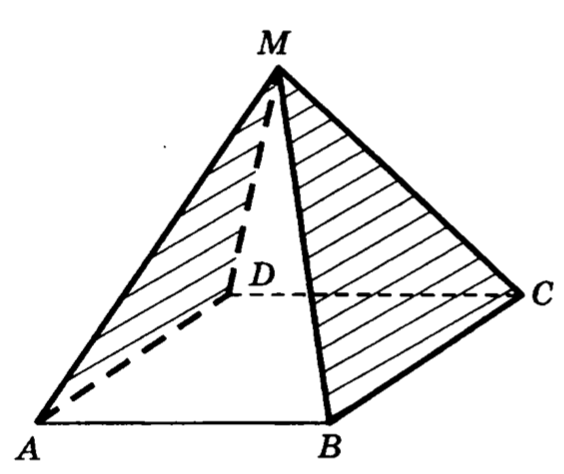
29. В правильной четырехугольной пирамиде все ребра которой равны , найти угол между плоскостями и .
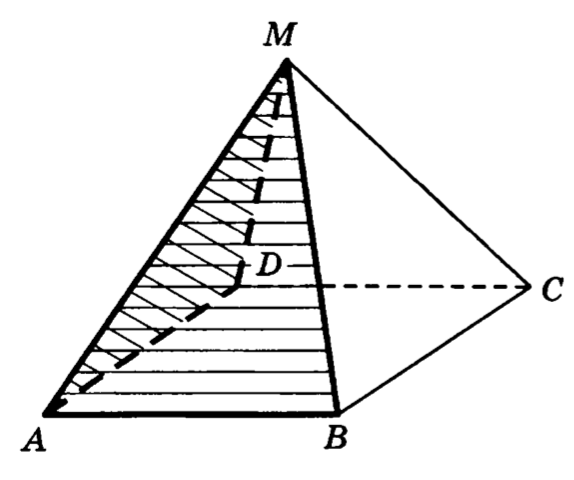
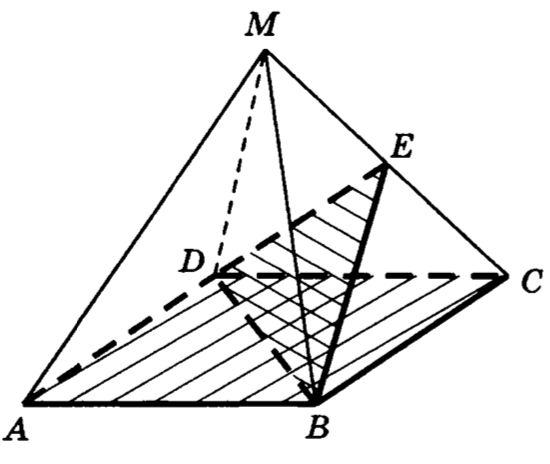
30. В правильной четырехугольной пирамиде все ребра которой равны , найти угол между плоскостями и .
Г4. Перпендикуляр и наклонные. Угол между прямой и плоскостью
By vkrysanov320
Г4. Перпендикуляр и наклонные. Угол между прямой и плоскостью
- 2,039



