Расстояния между скрещивающимися прямыми
10 класс
vkrysanov320@gmail.com
version 1.0 not-fixed, 16-04-2023Расстояние между скрещивающимися прямыми (I)
Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра.
a
b
M
M'
\rho(a; b)
\begin{cases}
\\
\\
\\
\end{cases}
MM'\perp a
MM'\perp b
\begin{cases}
\\ \\\\
\end{cases}
\Rightarrow \rho(a; b) = MM'.
a ∸ b
Скрещивающиеся прямые – это прямые, через которые нельзя провести одну плоскость.
Вытекает из определения расстояния между двумя фигурами: расстояние между двумя фигурами называется расстояние между ближайшими точками этих фигур (если такие точки имеются).
* a ∸ b
Задачи (I)
1. Прямая перпендикулярна плоскости . Т.н.: .
ABC
\rho(a, AC)
a
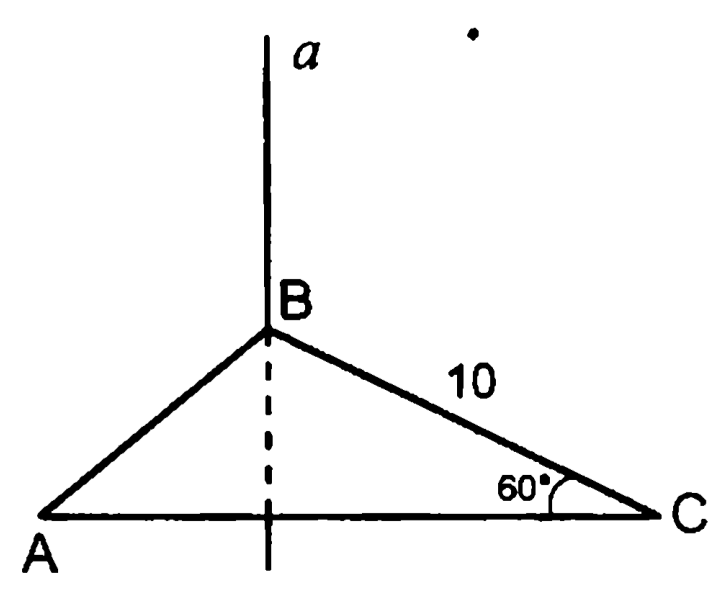
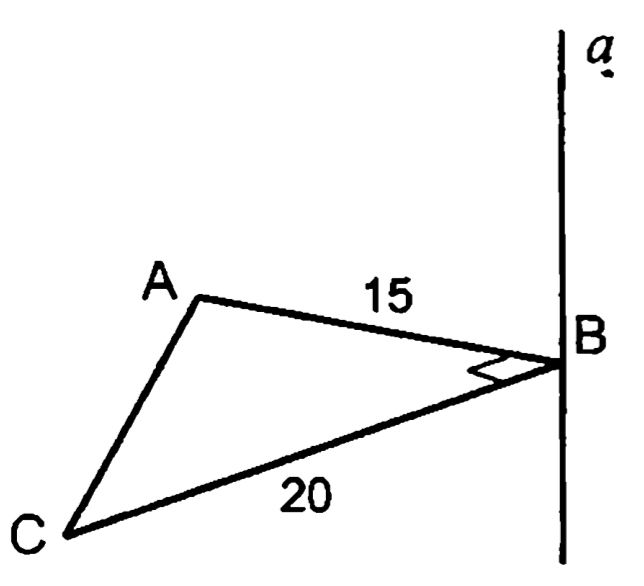
2. Прямая перпендикулярна плоскости . Т.н.: .
ABC
\rho(a, AC)
a
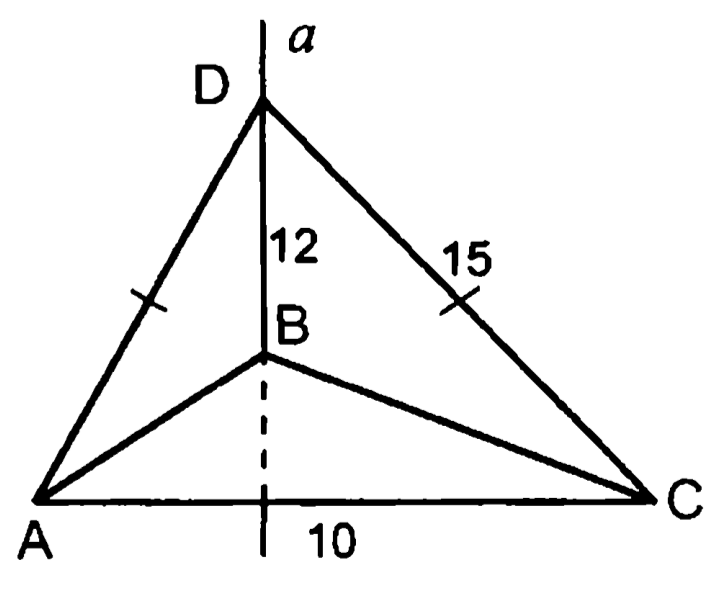
3. Прямая перпендикулярна плоскости . Т.н.: .
ABC
\rho(a, AC)
a
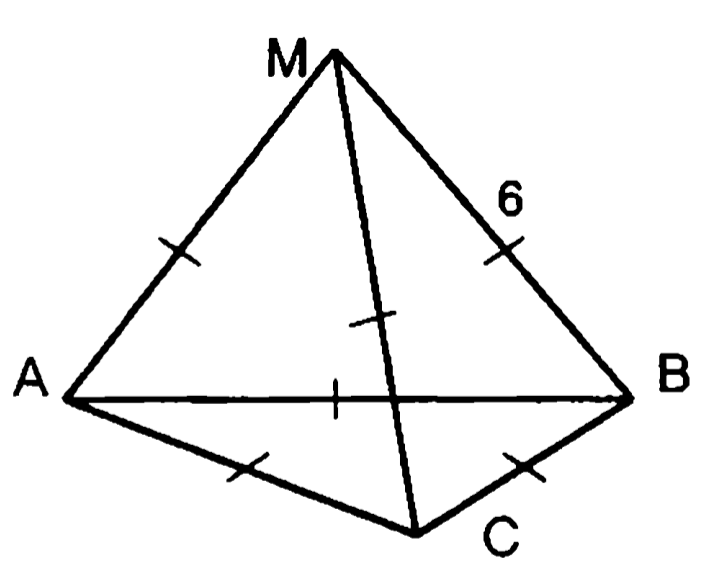
4. Точка лежит вне плоскости
M
ABC.
Т.н.: .
\rho(BM, AC)
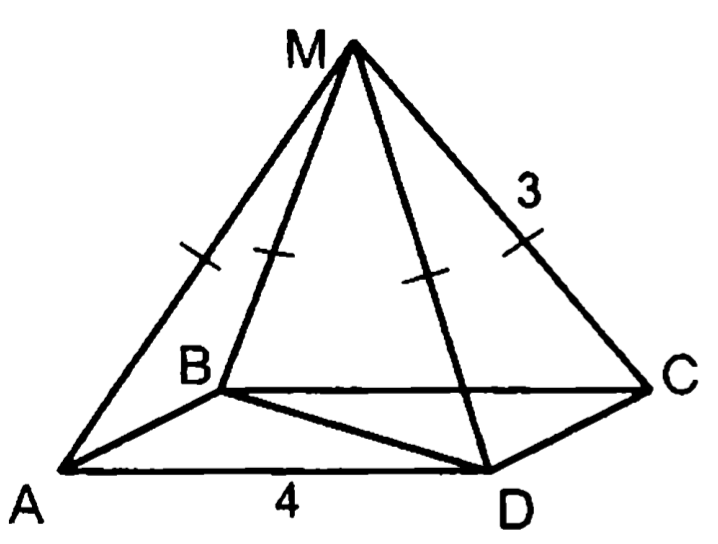
5. Точка лежит вне плоскости
M
ABC.
Т.н.: .
\rho(AM, BD)
ABCD
— квадрат.
Расстояние между скрещивающимися прямыми — это расстояние между одной из этих прямых и плоскостью, проходящей через вторую прямую параллельно первой.
Расстояние между скрещивающимися прямыми (II)
a
b
a
b
a
b
Шаг 1. «Обернуть» одну из прямых в плоскость, которая будет параллельна второй прямой.
Шаг 2. Опустить перпендикуляр из любой точки второй прямой на проведенную плоскость (он и будет искомым расстоянием).
\rho(a; b)
\begin{cases}
\\
\\
\\
\end{cases}
M
\alpha
\alpha
M'
* a ∸ b
MM' \perp \alpha, M \in a
\begin{cases}
\\
\\
\\
\\
\end{cases}
\rho(a; b) = MM'.
\Leftarrow
Расстояние между скрещивающимися прямыми — это расстояние между параллельными плоскостями, в которых находятся скрещивающиеся прямые.
Расстояние между скрещивающимися прямыми (III)
\alpha \parallel \beta
M_1M_2 \perp \alpha
\begin{cases}
\\
\\
\\
\end{cases}
\rho(a; b) = \rho(\alpha; \beta) .
\Leftarrow
a
b
\alpha
\beta
\begin{cases}
\\
\\
\\
\end{cases}
M_1
\rho(a; b)
M_2
a \in \alpha, b \in \beta
a ∸ b
1.
2.
M_1M_2 \perp \beta
\begin{cases}
\\
\\
\end{cases}
\rho(\alpha; \beta) = M_1M_2.
\Leftarrow
Расстояние между скрещивающимися прямыми — это расстояние между их проекциями на плоскость, которая перпендикулярна одной из этих прямых.
Расстояние между скрещивающимися прямыми (IV)
a
b
\begin{cases}
\\
\\
\end{cases}
\rho(a; b)
b \perp \alpha
\alpha
a
— наклонная к
\alpha
M
Q
H
P
T
PH
— проекция на
a
\alpha
MH \perp \alpha, M \in \alpha
\begin{cases}
\\
\\
\\
\end{cases}
\rho(a; b) = \rho(PH; T) .
\Leftarrow
1.
2.
\rho(PH; T) = HT,
т.к.
PH \perp HT.
проекция перпендикулярной к плоскости прямой на на эту плоскость — точка
Задачи
1. В кубе , ребро которого равно найти расстояние между и .
ABCDA_1...D_1
\sqrt{32}
DB_1
CC_1
2. В единичном кубе , найти расстояние между и .
ABCDA_1...D_1
AC
BB_1
4. В правильной треугольной призме , все ребра которой равны 1, найти расстояние между прямыми и .
ABCA_1B_1C_1
AB
B_1C_1
5. В единичном кубе , найти расстояние между и .
ABCDA_1...D_1
CD
BB_1
3. В единичном кубе , найти расстояние между и .
ABCDA_1...D_1
AA_1
BD_1
6. В единичном кубе , найти расстояние между и .
ABCDA_1...D_1
BA_1
CC_1
7. В правильной треугольной призме , все ребра которой равны 1, найти расстояние между прямыми и .
ABCA_1B_1C_1
BB_1
AC
8. В правильной треугольной призме , все ребра которой равны 1, найти расстояние между прямыми и .
ABCA_1B_1C_1
AB_1
BC
Задачи (2)
9. Основанием прямой треугольной призмы является
прямоугольный треугольник с прямым углом . Грань является квадратом.
а) Доказать, что прямые и перпендикулярны.
б) Найти расстояние между прямыми и , если , .
ABCA_1B_1C_1
ACC_1A_1
C
ABC
CA_1
AB_1
CA_1
AB_1
AC= 4
BC = 7
10. Основание пирамиды — квадрат . Боковое ребро
перпендикулярно плоскости основания.
а) Доказать, что плоскости и перпендикулярны.
б) Найти расстояние между прямыми и , если сторона основания
равна , а высота пирамиды равна .
SABCD
ABCD
SA
ASD
CSD
SC
BD
2
2\sqrt{2}
11. В правильной треугольной призме все ребра равны . Точка — середина ребра .
а) Доказать, что прямые и перпендикулярны.
б) Найдите расстояние между прямыми и .
ABCA_1B_1C_1
2
M
AA_1
MB
B_1C
MB
B_1C
Задачи (3)
12. Дан правильный тетраэдр MABC с ребром 1. Найдите расстояние между прямыми AL и MO, где L — середина ребра MC, O — центр грани ABC.
13. В правильной четырёхугольной пирамиде SABCD (с вершиной S) длина каждого ребра равна 4. Точка K — середина ребра SA. Найдите расстояние между прямыми AD и BK.
14. В правильной четырёхугольной пирамиде сторона основания равна , а боковое ребро равно . На рёбрах CD и SC отмечены точки N и K соответственно, причём DN : NC= SK : KC = 1 : 7. Плоскость α содержит прямую KN и параллельна прямой BC.
а) Докажите, что плоскость делит ребро в отношении , считая от вершины .
б) Найдите расстояние между прямыми и .
S
SA
KN
\alpha
SB
1:7
SABCD
AB
8
SA
10
Г6. Расстояние между скрещивающиеся прямыми
By vkrysanov320
