Многогранники
10 класс
vkrysanov320@gmail.com
version 1.0 not-fixed, 20-01-2023Понятие многогранника
Поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело называется многогранной поверхностью или многогранником.
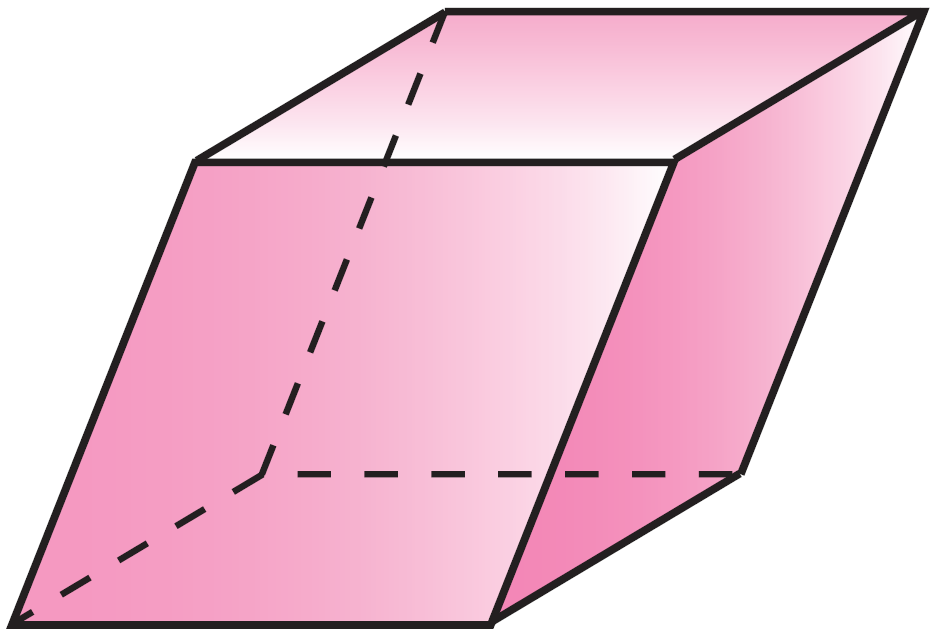
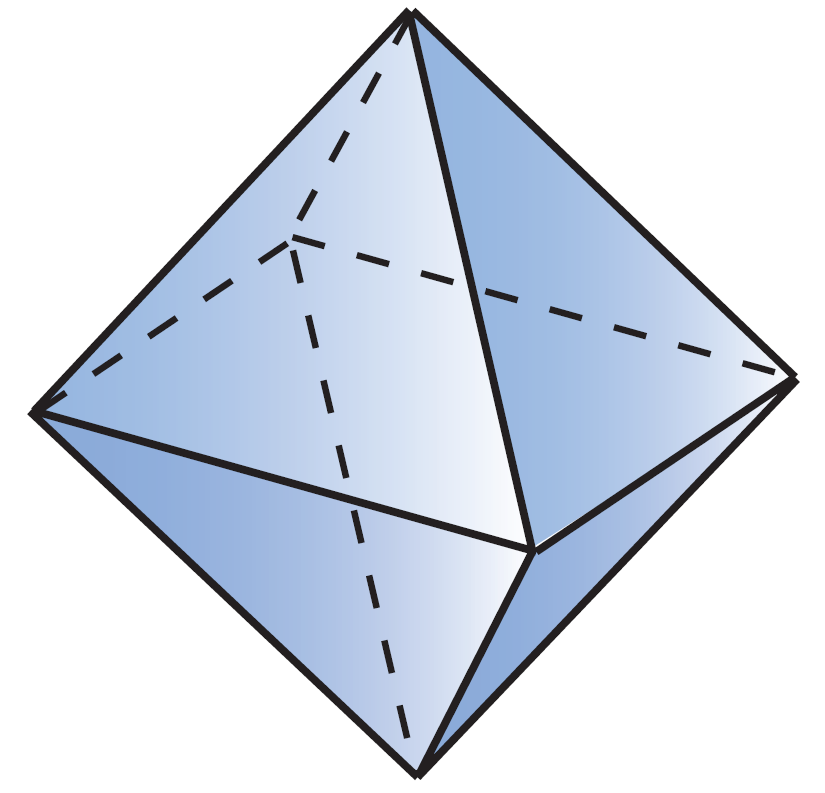
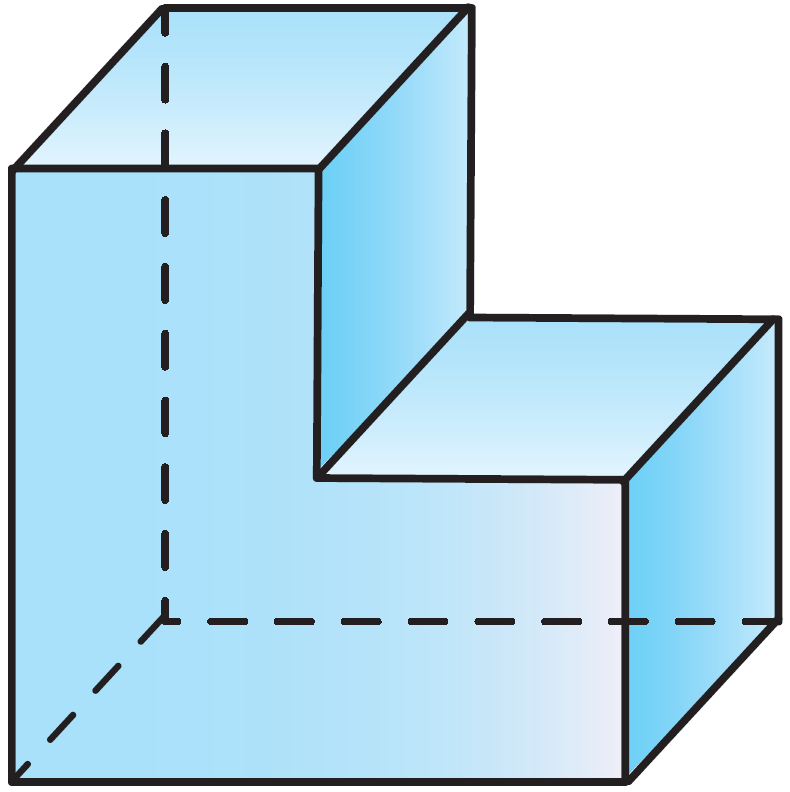
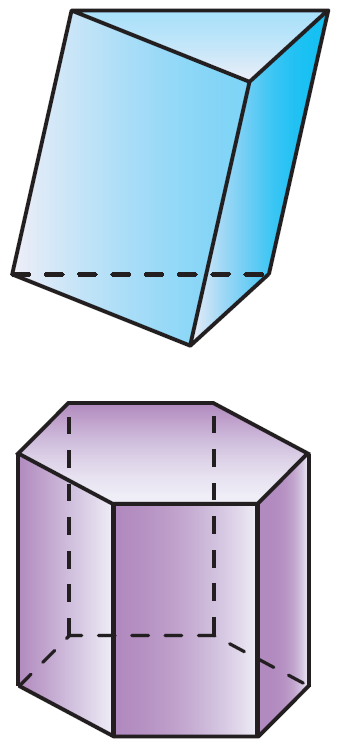
Многогранники
выпуклые
невыпуклые
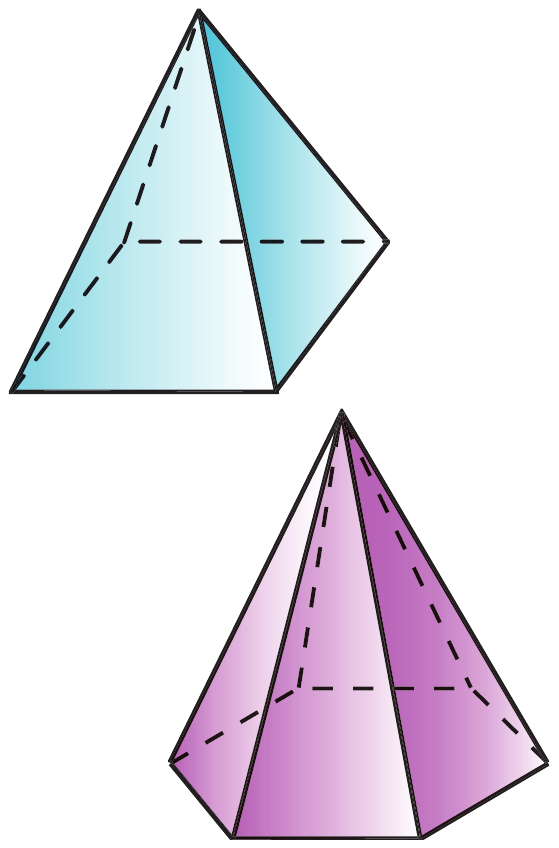
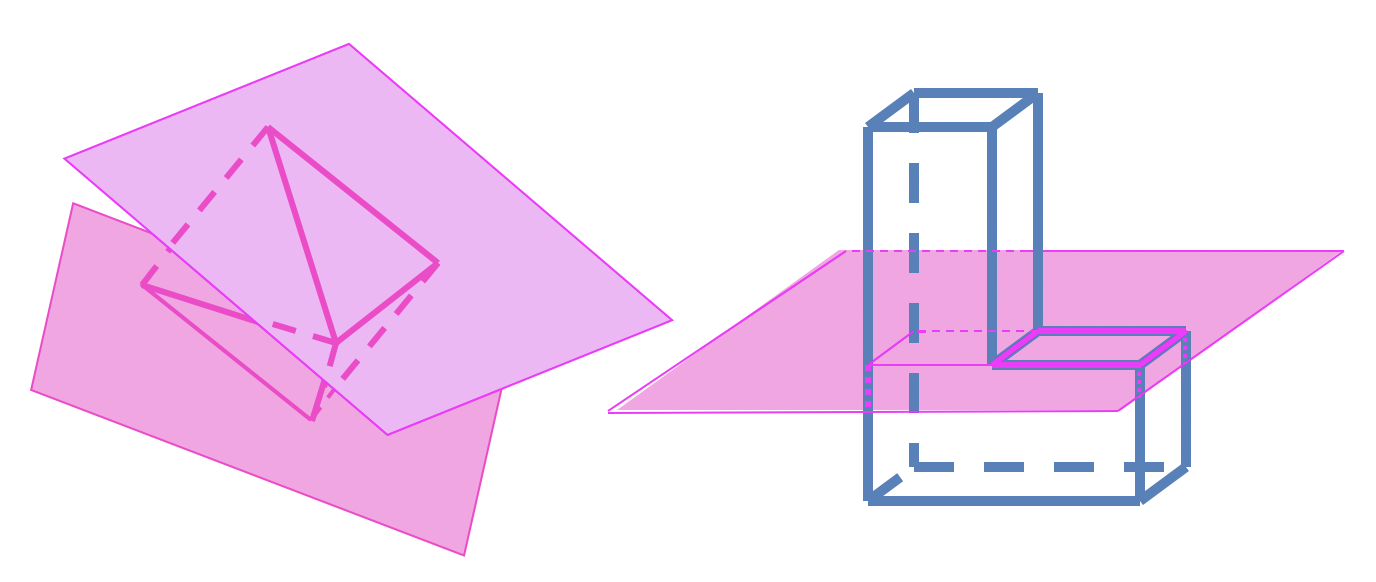
Призма
Призма — многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками.
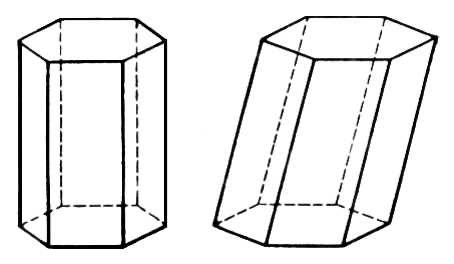
Если боковые ребра призмы перпендикулярны основаниям то призма называется прямой, в противном случае — наклонной.
h
высота призмы
прямая
наклонная
* высота перпендикулярна обоим основаниям
Призма называется правильной, если она прямая и ее основания — правильные многоугольники.
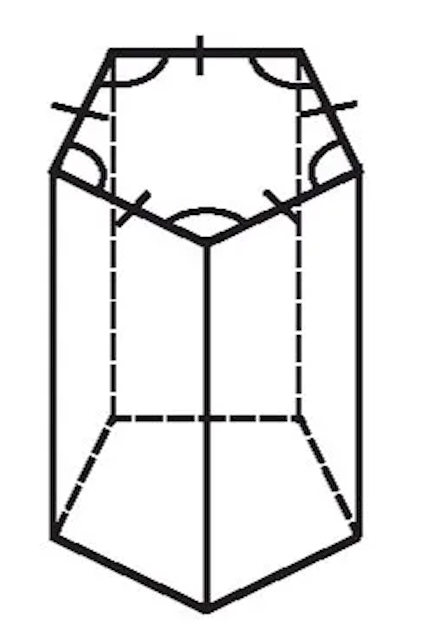
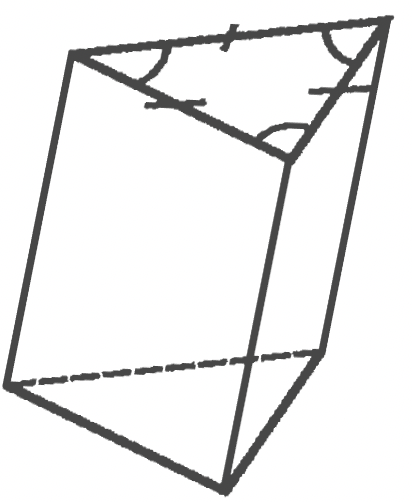
прямая пятиугольная
треугольная
Площадь поверхности призмы
S_1
S_2
S_3
S_4
S_n
S_1 ... S_n
— площади боковых пов-тей
S_{бок} = S_1 + S_2 + ... + S_n = P_{пс}l
S_{полн} = S_{бок} + 2S_{осн}
S_{осн}
\begin{cases}
\\
\\
\\
\\
\\
\\
\end{cases}
l
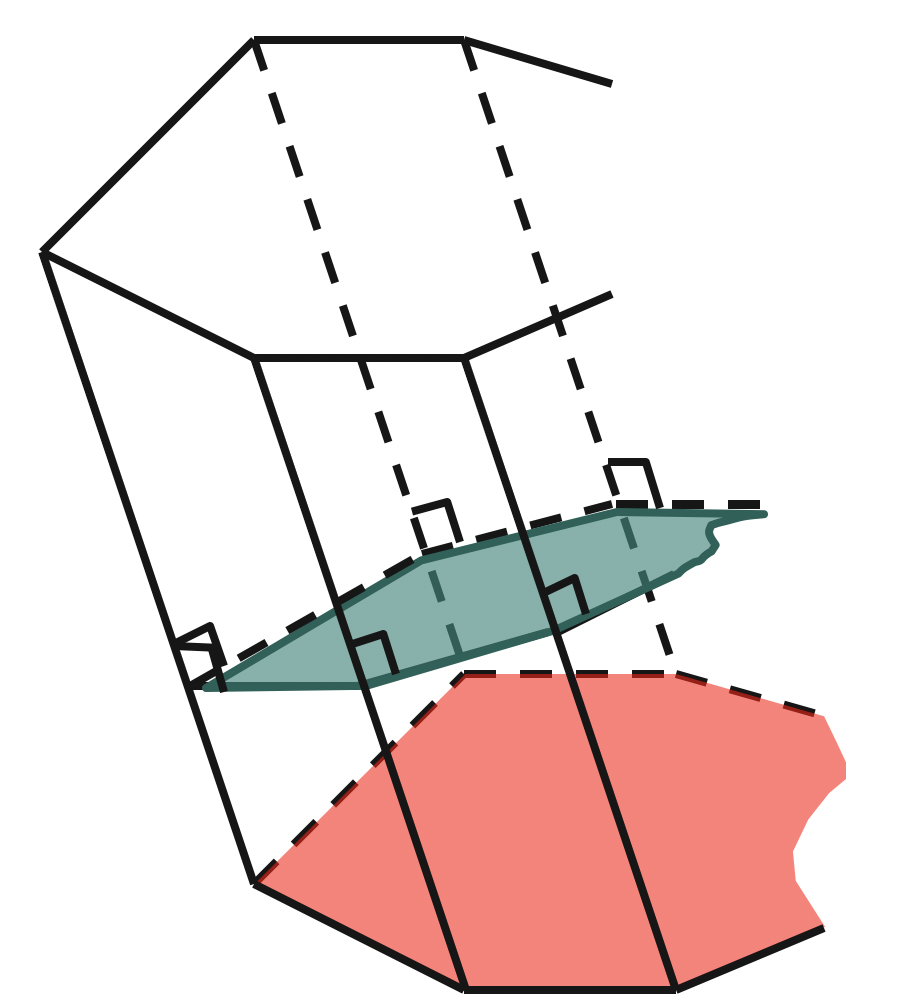
перпендикулярное сечение
S_{бок} = P_{осн}h
для прямой призмы
\begin{cases}
\\
\\
\\
\\
\\
\\
\end{cases}
\begin{cases}
\\
\\
\\
\\
\\
\end{cases}
h
S_1
S_2
S_3
S_4
S_n
S_{осн}
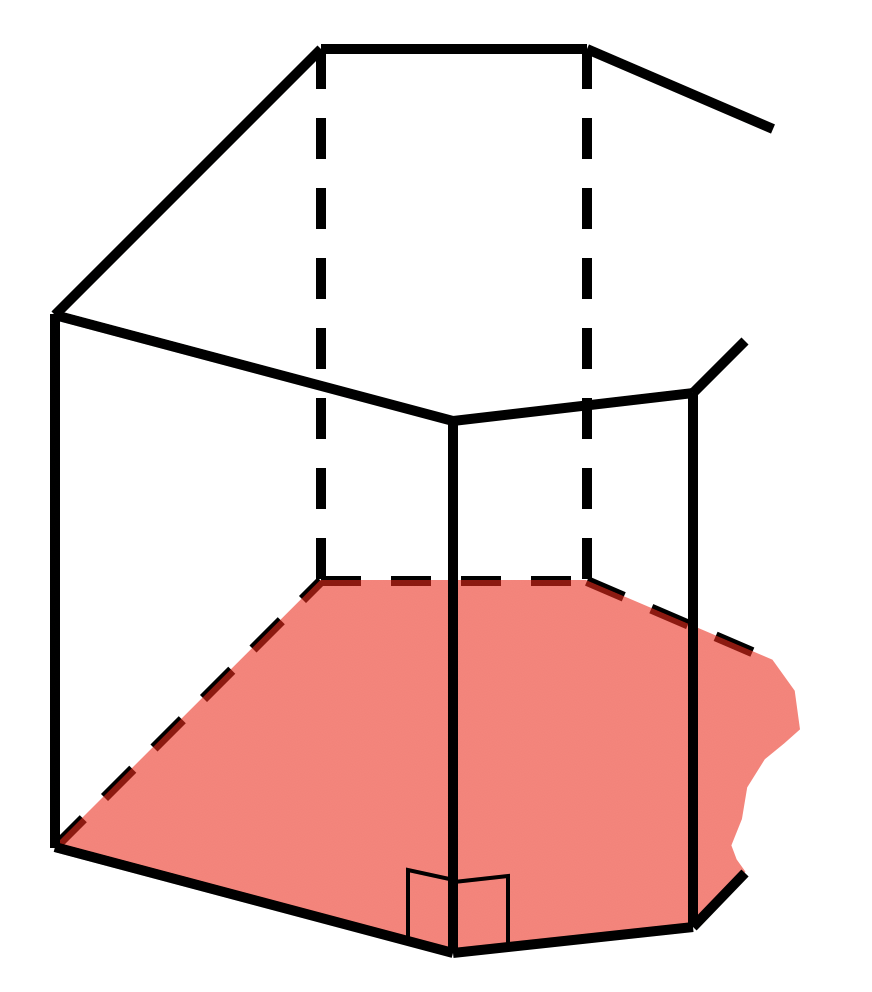
Задачи
1. Расстояния между ребрами наклонной треугольной призмы равны: и . Боковая поверхность призмы — . Найти ее боковое ребро.
2. Сторона основания правильной треугольной призмы равна , а диагональ боковой грани . Найти площадь боковой и полной поверхности призмы.
3. Боковое ребро правильной треугольной призмы равно , а диагональ боковой грани равна . Найти площадь боковой и полной поверхности призмы.
4. Основание прямой призмы — прямоугольный треугольник с катетами и 20. Большая боковая грань и основание призмы равновелики. Найти площадь боковой и полной поверхности призмы.
5. Основание прямой призмы — прямоугольный треугольник с гипотенузой 25 и катетом 20. Меньшая боковая грань и основание призмы равновелики. Найти площадь боковой и полной поверхности призмы.
6. Диагональ правильной четырехугольной призмы образует с плоскостью боковой грани угол в . Найти угол между диагональю и плоскостью основания.
45 \text{ } ед^{2}
2, 3
4
30^{\circ}
10
6
15
9
15
Задачи (2)
7. Дана прямая призма, в основании которой лежит равнобедренная описанная около окружности трапеция с боковой стороной, равной , и высотой, равной . Боковое ребро призмы равно . Найдите площадь полной поверхности призмы.
8. Сторона основания правильной четырехугольной призмы равна , диагональ призмы образует с плоскостью основания угол градусов. Найти диагональ призмы, площадь боковой поверхности призмы, угол между диагональю призмы и плоскостью боковой грани.
5
3
2
45^{\circ}
a
Пирамида
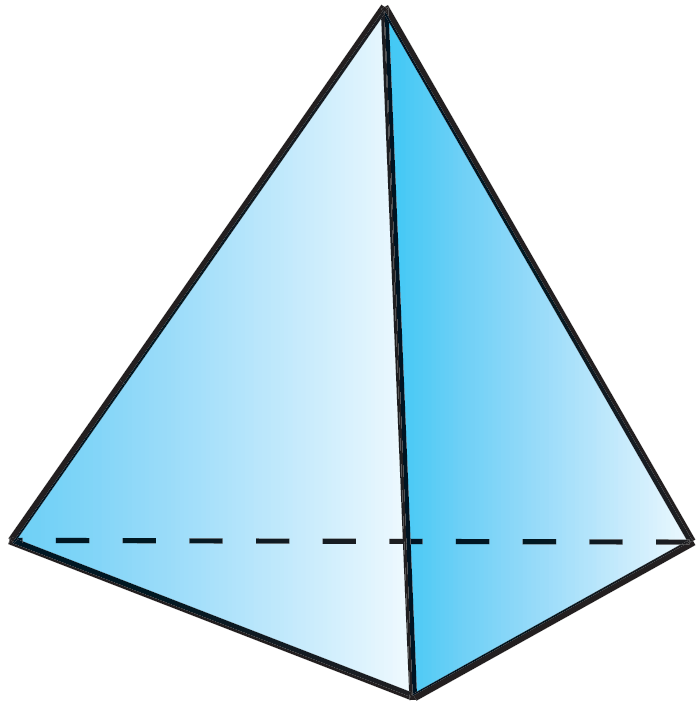
Пирамида — многогранник, одна из граней которого (называемая основанием) — произвольный многоугольник, а остальные грани (называемые боковыми гранями) — треугольники, имеющие общую вершину.
Пирамида называется правильной, если в основании лежит правильный многоугольник (все углы равны и все стороны равны) и выполнено одно из эквивалентных условий:
h
высота пирамиды
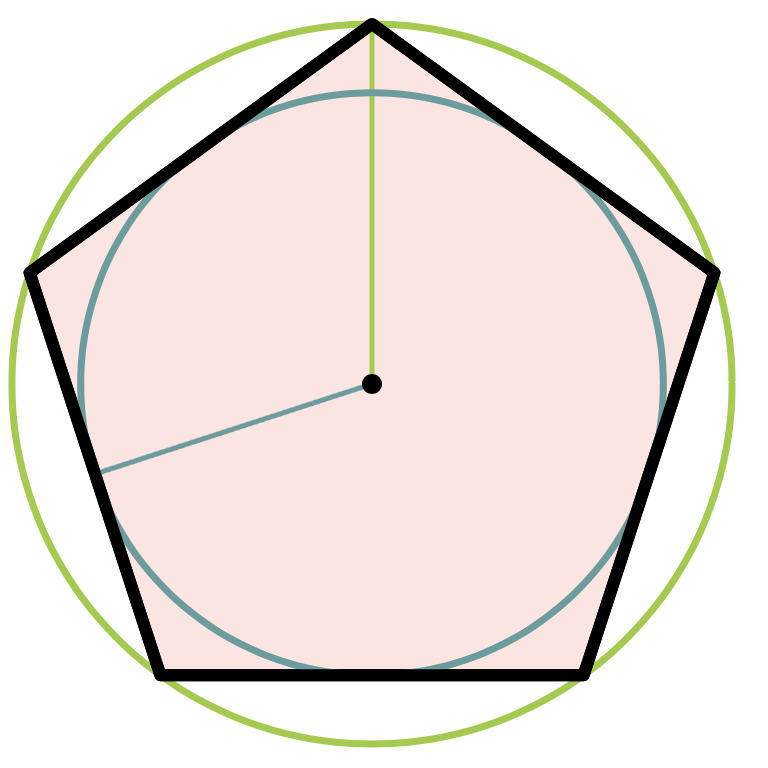
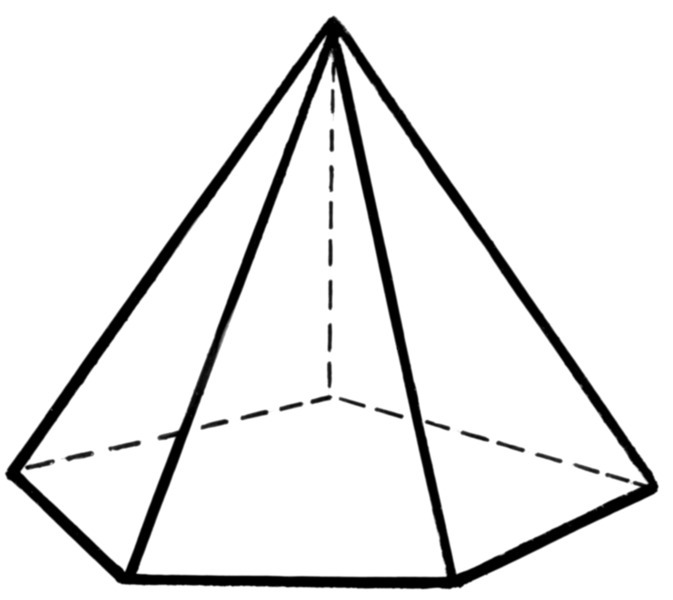
плоскость основания
- боковые ребра равны;
- высота пирамиды проходит через центр описанной около основания окружности;
- боковые ребра наклонены к основанию под одинаковым углом.
h
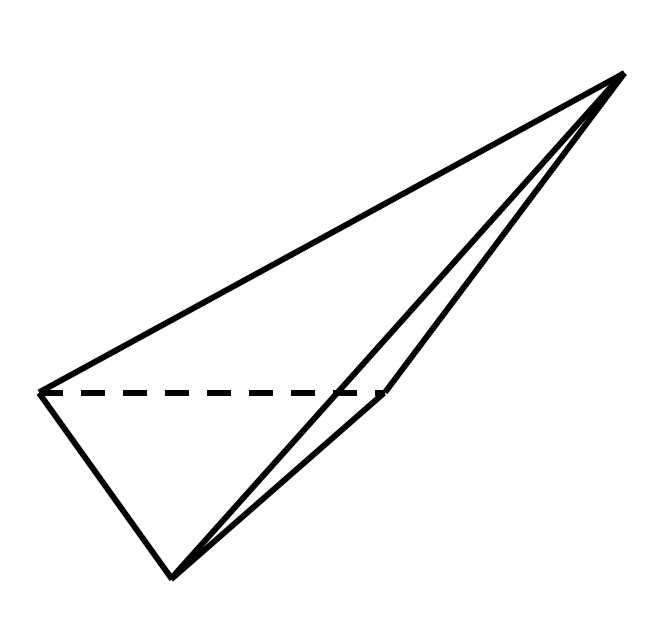
высота пирамиды
пример неправильной пирамиды:
Площадь поверхности пирамиды
S_{бок} = S_1 + S_2 + ... + S_n
S_1
S_2
S_3
S_4
S_n
S_{осн}
S_1 ... S_n
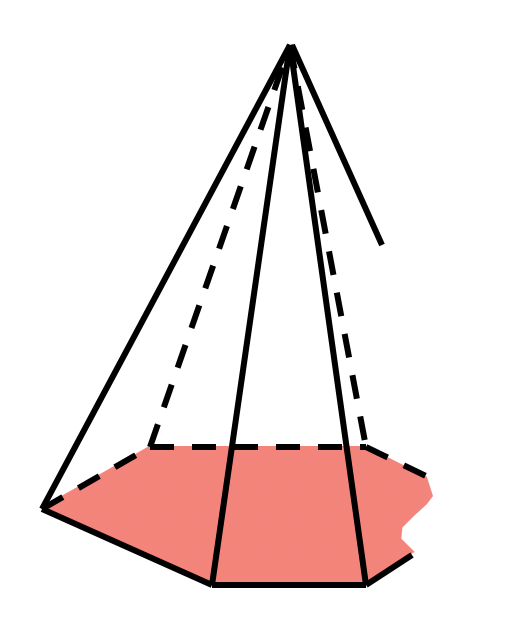
— площади боковых пов-тей
в основании произвольный многоугольник
апофема
S_{бок} = \frac{1}{2}P_{осн}l_a = \frac{S_{осн}}{\cos \varphi}
для правильной пирамиды
l_a
\begin{cases}
\\
\\
\\
\\
\\
\\
\\
\\
\end{cases}
S_{осн}
S_1
S_2
S_3
S_4
S_n
S_{полн} = S_{бок} + S_{осн}
\varphi
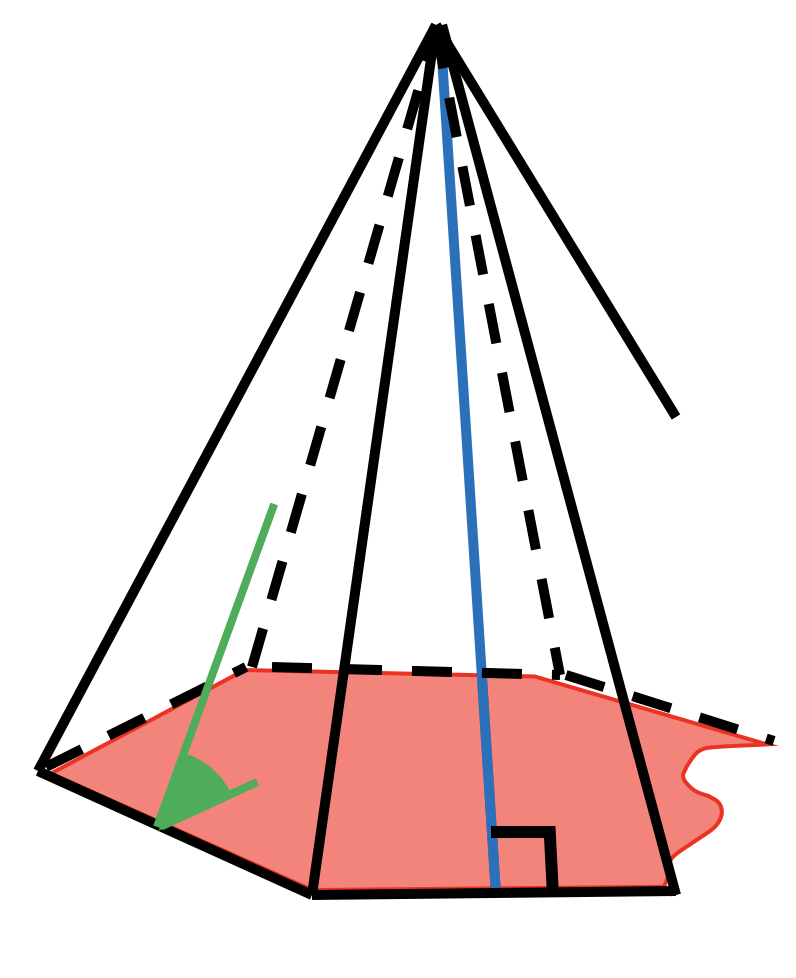
двугранный угол при основании пирамиды
Свойство точки, равноудаленной от сторон многоугольника
M
N
Q
O
S
Если прямая, перпендикулярная плоскости многоугольника, проходит через центр вписанной в многоугольник окружности, то каждая точка этой прямой равноудалена от сторон многоугольника.
SO \perp ABC,
O
— центр вписанной окруж-ти в
\Rightarrow
\begin{cases}
\\
\\
\\
\\
\\
\\
\\
\end{cases}
\rho(S; AB) = \rho(S; BC) = \rho(S; CA)
\triangle ABC
A
B
B
C
\rho(S_1; AB) = \rho(S_1; BC) = \rho(S_1; CA)
\rho(O; AB) = \rho(O; BC) = \rho(O; CA)
S_1
Свойство точки, равноудаленной от сторон многоугольника (2)
M
N
Q
O
S
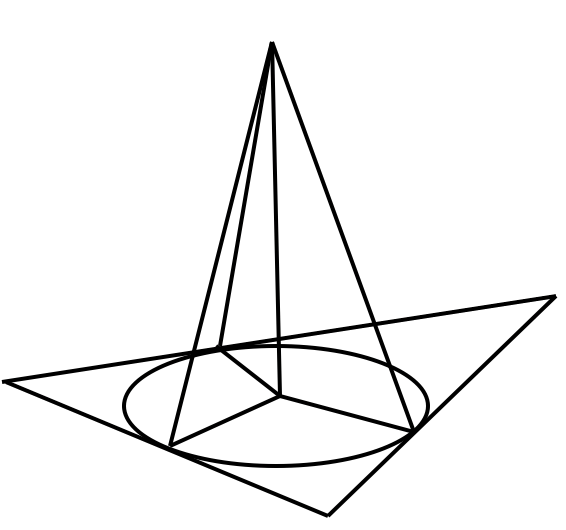
Если точка, не лежащая в плоскости выпуклого многоугольника, равноудалена от сторон многоугольника, то основание перпендикуляра, проведенного из этой точки к плоскости, является центром окружности, вписанной в многоугольник.
O
— центр вписанной окруж-ти в
\Rightarrow
\begin{cases}
\\
\\
\\
\\
\\
\\
\\
\end{cases}
\rho(S; AB) = \rho(S; BC) = \rho(S; CA), SO \perp ABC
\triangle ABC
A
B
B
C
Свойство точки, равноудаленной от вершин многоугольника
A
B
C
O
S
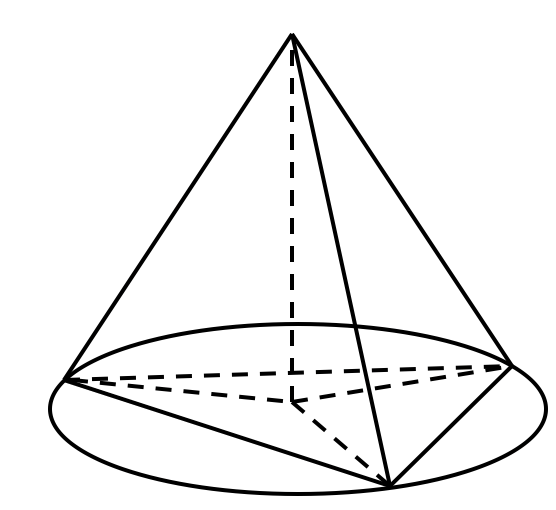
Если прямая, перпендикулярная плоскости многоугольника, проходит через центр описанной около многоугольника окружности, то каждая точка этой прямой равноудалена от вершин многоугольника.
SO \perp ABC,
O
— центр описанной окруж-ти у
\Rightarrow
S_1
S_2
\rho(S_1; A) = \rho(S_1; B) = \rho(S_3; C)
\rho(S_2; A) = \rho(S_2; B) = \rho(S_2; C)
\rho(O; A) = \rho(O; B) = \rho(O; C)
\begin{cases}
\\
\\
\\
\\
\\
\\
\\
\end{cases}
\rho(S; A) = \rho(S; B) = \rho(S; C)
\triangle ABC
Свойство точки, равноудаленной от вершин многоугольника (2)
A
B
C
O
S
Если точка, не лежащая в плоскости выпуклого многоугольника, равноудалена от вершин многоугольника, то основание перпендикуляра, проведенного из этой точки к плоскости, является центром окружности, описанной около многоугольника.
O
— центр описанной окружности у
\Rightarrow
\begin{cases}
\\
\\
\\
\\
\\
\\
\\
\end{cases}
\rho(S; A) = \rho(S; B) = \rho(S; C), SO \perp ABC
\triangle ABC
...
- Множество всех точек пространства, равноудаленных от сторон данного треугольника, есть прямая, перпендикулярная плоскости треугольника, проходящая через центр вписанной в него окружности. На этой прямой лежат центры всех шаров, касающихся сторон треугольника.
- Множество всех точек пространства, равноудаленных от трех данных точек, не лежащих на одной прямой, есть прямая, перпендикулярная плоскости этих точек и проходящая через центр окружности, описанной около треугольника с вершинами в данных точках. Этой прямой принадлежат центры всех сфер, проходящих через данные точки
Задачи
1. Стороны основания правильной четырехугольной пирамиды равны , боковые ребра равны . Найдите площадь поверхности этой пирамиды.
2. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны и высота равна .
3. Площадь боковой поверхности правильной пятиугольной пирамиды равна . Чему будет равна площадь боковой поверхности пирамиды, если все ее ребра уменьшить в раза?
4. DACB — пирамида с треугольником в основании; ,
Найти площадь бокового сечения.
5. Апофема правильной четырехугольной пирамиды равна , высота пирамиды — Найти сторону основания пирамиды, угол между боковой гранью и плоскостью основания пирамиды, угол, образованный боковым ребром и плоскостью основания пирамиды, площадь боковой поверхности пирамиды, площадь полной поверхности пирамиды.
AB = AC = 13, AD \perp ABC
ACB
72
164
6
4
4
13
2
AD = 9.
6
3\sqrt{2}.
Задачи (2)
SABC
AB
6
SA
7
AB
SC
K
M
AK:KB = SM:MC = 1:5
\alpha
KM
BC
\alpha
SA
\alpha
SBC
6*. В правильной треугольной пирамиде сторона основания равна , а боковое ребро равно . На рёбрах и отмечены точки и соответственно, причём . Плоскость содержит прямую и параллельна прямой .
а) Доказать, что плоскость параллельна прямой .
б) Найти угол между плоскостями и .
SABC
AB
SA
7
AB
SC
K
M
AK:KB = SM:MC = 1:5
\alpha
KM
BC
\alpha
SA
\alpha
SBC
SABC
AB
5
SA
3
AB
SC
K
M
AK:KB = SM:MC = 1:4
\alpha
KM
BC
\alpha
SA
\alpha
SBC
7*. В правильной треугольной пирамиде сторона основания равна , а боковое ребро равно . На рёбрах и отмечены точки и соответственно, причём . Плоскость содержит прямую и параллельна прямой .
а) Доказать, что плоскость параллельна прямой .
б) Найти угол между плоскостями и .
Задачи (3)
8. Основанием пирамиды является ромб, сторона которого равна , а одна из диагоналей . Найти боковые ребра пирамиды, если ее высота проходит через точку пересечения диагоналей основания и равна .
9. Основанием пирамиды является треугольник , у которого ,
7
8
5
DABC
ABC
AB = AC = 13
BC = 10
; ребро перпендикулярно к плоскости основания и равно . Найти
площадь боковой поверхности пирамиды.
AD
9
10. Основанием пирамиды является прямоугольный треугольник , у которого гипотенуза , катет . Ребро перпендикулярно к плоскости основания и равно . Найти площадь боковой поверхности пирамиды.
11. Основанием пирамиды является параллелограмм, стороны которого равны и , а площадь равна . Высота пирамиды проходит через точку пересечения диагоналей основания и равна . Найти площадь полной поверхности пирамиды.
12. Основанием пирамиды является прямоугольник, диагональ которого равна . Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы в и . Найти площадь полной поверхности пирамиды.
DABC
ABC
AB = 29
AC = 21
AD
20
20
36
360 \text{ ед}^2
12
8
30^{\circ}
45^{\circ}
Задачи (4)
13. Высота треугольной пирамиды равна , а высота каждой боковой грани, проведенная из вершины пирамиды, равна .
а) Доказать, что высота пирамиды проходит через центр окружности, вписанной в ее основание.
б) Найти площадь основания пирамиды, если его периметр равен .
14. Основанием пирамиды является треугольник с сторонами . Каждая боковая грань наклонена к основанию под углом . Найти площадь боковой поверхности пирамиды.
15. Основанием пирамиды является равнобедренный треугольник с углом 120°. Боковые ребра образуют с ее высотой, равной , углы в . Найти площадь основания пирамиды.
16. Основанием пирамиды является прямоугольный треугольник с гипотенузой . Боковые ребра пирамиды равны друг другу, а ее высота равна . Найти боковое ребро пирамиды, если .
40
42
12, 10, 10
41
45^{\circ}
45^{\circ}
16
DABC
BC
12
BC = 10
Усеченная пирамида
Усеченной пирамидой называется многогранник, заключенный между основанием пирамиды и секущей плоскостью, параллельной ее основанию.
-
Основания усеченной пирамиды — подобные многоугольники
-
Боковые грани усеченной пирамиды — трапеции.
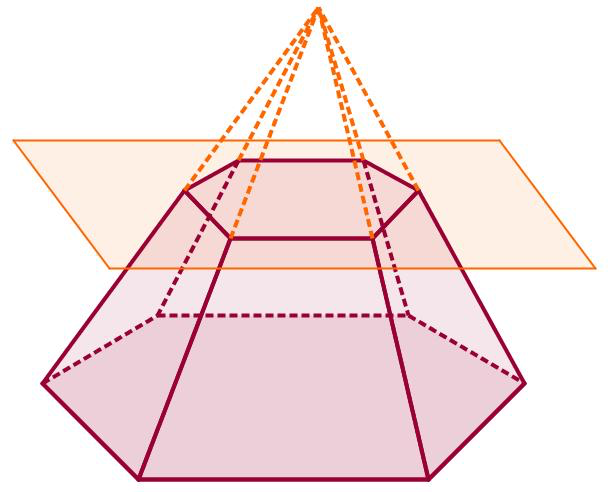
Усеченная пирамида, полученная из правильной пирамиды, называется правильной усеченной пирамидой.
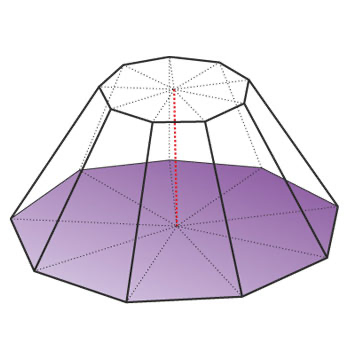
- Боковые ребра правильной усеченной пирамиды равны и одинаково наклонены к основанию пирамиды.
- Боковые грани правильной усеченной пирамиды — равные между собой равнобедренные трапеции и одинаково наклонены к основанию пирамиды.
- Двугранные углы при боковых ребрах правильной усеченной пирамиды равны.
* Свойства проекции вершины на основание аналогичны обыкновенным пирамидам.
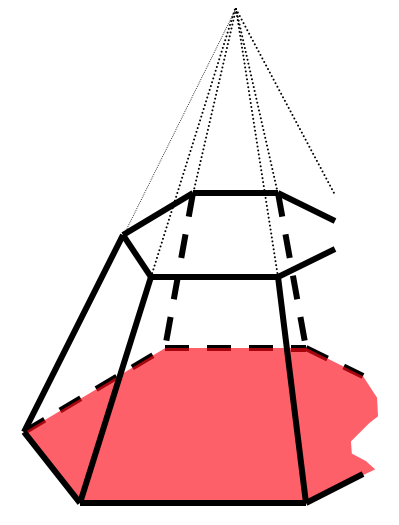
Площадь поверхности усеченной пирамиды
S_{бок} = S_1 + S_2 + ... + S_n
S_1
S_2
S_3
S_4
S_n
S_{н.осн}
S_1 ... S_n
— площади боковых пов-тей
в основании произвольный многоугольник
S_{бок} = \frac{1}{2}(P_{н.осн} + P_{в.осн})l_a =
для правильной усеченной пирамиды пирамиды
S_{полн} = S_{бок} + S_{н.осн} + S_{в.осн}
апофема
\begin{cases}
\\
\\
\\
\\
\\
\end{cases}
= \frac{S_{н.осн} - S_{в.осн}}{\cos \varphi}
\varphi
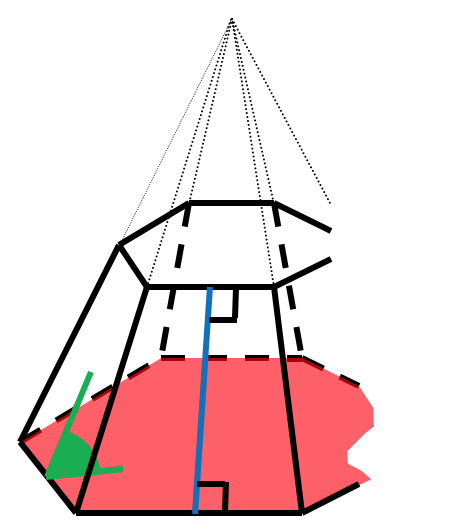
двугранный угол при основании пирамиды
S_{н.осн}
S_1
S_2
S_3
S_n
S_{в.осн}
S_{в.осн}
Задачи
1. В правильной четырехугольной усеченной пирамиде стороны оснований равны 22 и 6, а высота — 13. Вычислить площадь полной поверхности пирамиды.
2. В правильной четырехугольной усеченной пирамиде стороны оснований равны 24 и 8, а высота — 15. Вычислите площадь полной поверхности пирамиды.
3. Стороны оснований правильной треугольной усеченной пирамиды равны 4 и 2, а боковое ребро равно 2. Найти высоту и апофему пирамиды.
4. Основаниями усеченной пирамиды являются правильные треугольники со сторонами 5 и 3 соответственно. Одно из боковых ребер пирамиды перпендикулярно к плоскостям оснований и равно 1. Найти площадь боковой поверхности усеченной пирамиды.
5. Стороны оснований правильной четырехугольной усеченной пирамиды равны 4 и 4; боковая грань наклонена к плоскости основания под углом . Найти полную поверхность пирамиды.
6. Боковое ребро правильной четырехугольной усеченной пирамиды равно и наклонено к плоскости основания под углом . Диагональ пирамиды перпендикулярна боковому ребру. Найти площадь меньшего основания пирамиды.
60^{\circ}
60^{\circ}
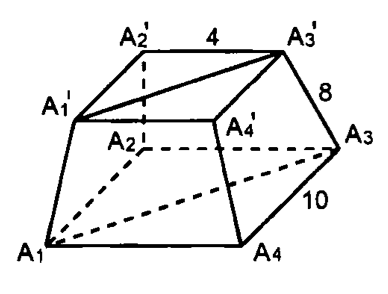
7.
Задачи
т.н.
S(A_1A'_1A'_3A_3)
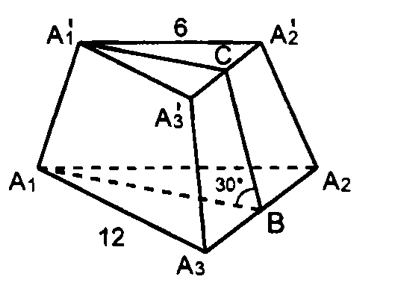
т.н.
S_{бок}
8.
В ниже приведенных задачах даны правильные усеченные пирамиды:
Г5. Многогранники
By vkrysanov320
