Ей было тысяча сто лет, она в сто первый класс ходила, с собою пó сто книг носила — всё это правда, а не бред!
Когда, пыля десятком ног,
она шагала по дороге,
за ней всегда бежал щенок
с одним хвостом, зато — стоногий!
Она ловила каждый звук
своими десятью ушами,
и десять загорелых рук
портфель и поводок держали.
И десять темно-синих глаз
рассматривали мир привычно...
С такой девчонкой необычной
и вы встречались, и не раз!
44 года назад
Системы счисления
10 класс
vkrysanov320@gmail.com
version 2.1, 26-09-2024
Системой счисления называется способ записи чисел.
Что такое система счисления?
Непозиционная система счисления — система счисления, в которой для обозначения чисел вводятся специальные знаки, количественное значение которых всегда одинаково и не зависит от их места в записи числа.
Типы систем счисления (1)
- Римская система счисления:
- Древнеегипетская десятичная система счисления:
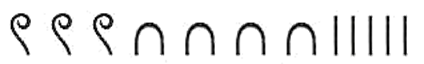
= 345 (Сумма эл-тов числа)
I, II, III, IV, V, VI, VII, VIII, IX, X, ...
Типы систем счисления (2)
Позиционная система счисления — система счисления, в которой значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда).
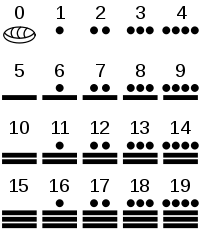
- Система счисления индейцев Майя:
- Арабская система счисления (десятичная):
0, 1,2,3,4,5,6,7,8,9,...
Позиционные системы счисления
Число в системе счисления с основанием , , записывают в виде последовательности его цифр, которые удовлетворяют неравенству , перечисляемых по убыванию старшинства разрядов слева направо:
В ненулевых числах начальные нули обычно опускаются:
b
0 \le x < b - 1
142_5, 542_6, 888_9, 777_7, 108_{10}.
Не может быть семеричным числом!
00782 \Rightarrow 782.
(b > 1)
\overline{a_n ... a_2a_1a_0}_b, b > 1, a_i \in \{0; 1; ...; b-1\}
Примеры:
Основные правила перевода
- Из десятичной в любую другую:
- Из любой другой в десятичную:
\overline{a_n ... a_2a_1a_0}_b = a_0 \cdot b^0 + a_1 \cdot b^1 + ... + a_n \cdot b^n =\sum\limits_{i = 0}^{n} a_i \cdot b^i.
Для перевода десятичного числа в с.c. c основанием его необходимо последовательно делить на до тех пор, пока не останется остаток, меньший или равный . Число в c.с. с основанием записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
b
b
b-1
b
Основные правила перевода. Пример
623_9 \rightarrow x_{10}:
623_9 = 6 \cdot 9^2 + 2 \cdot 9^1 + 3 \cdot 9^0 = 507_{10}.
2 1 0
Из любой другой в десятичную с.с.:
5B_{12} \rightarrow x_{10}:
5B_{12} = 5 \cdot 12^1 + 11 \cdot 12^0 = 60 + 11 = 71_{10}.
B = 11
1 0
Основные правила перевода. Пример (2)
507_{10} \rightarrow x_{9}:
71_{10} \rightarrow x_{12}:
Из десятичной в любую другую:
507
9
56
504
9
6
54
3
2
\Rightarrow 507_{10} = 623_{9}
71
12
5
60
11
=
B
\Rightarrow 71_{10} = 5B_{12}
Ещё один способ перевода...
HEX
BIN
BIN
OCT
\underbrace{001}_{1}\underbrace{011}_{3}{\underbrace{101}_{5}}{}_2 \Rightarrow 135_8
\underbrace{0101}_{5}{\underbrace{1101}_{D}}{}_2 \Rightarrow 5D_{16}
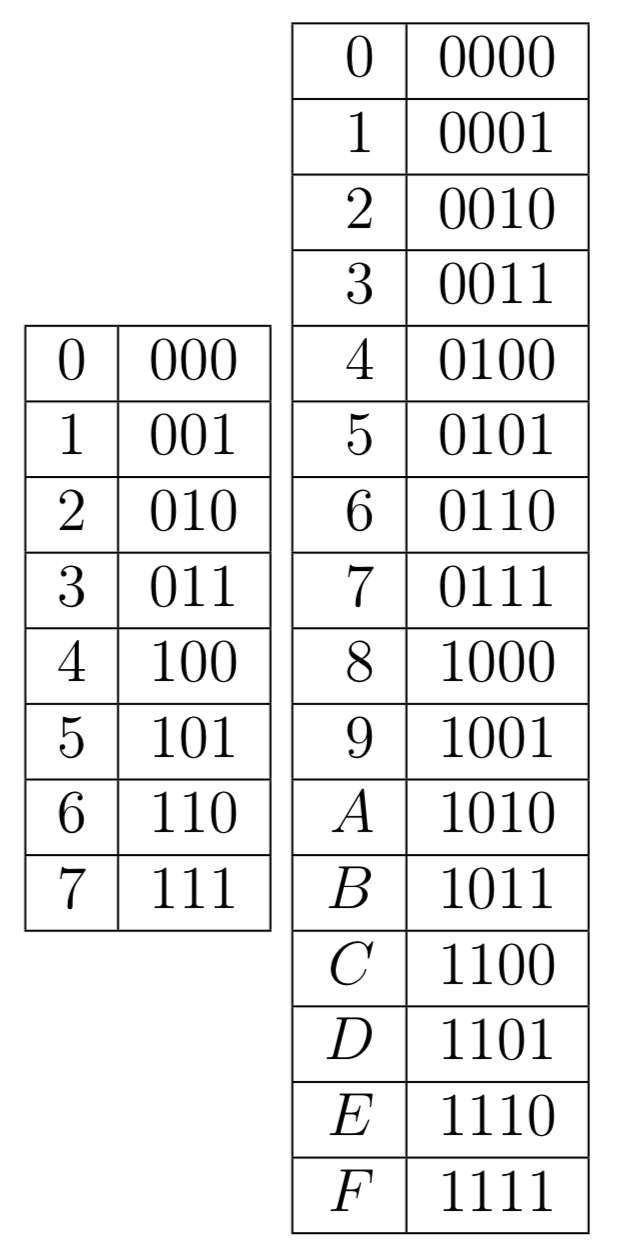
- в восьмеричную с.с. отделяем по три цифры с конца
- в шестнадцатеричную с.с. отделяем по четыре цифры с конца
Для перевод из двоичной в
Для обратного перевода каждая цифра в числе заменяется на три или четыре цифры двоичной системы счисления в соответствии с таблицей.
Системы счисления с отрицательным основанием
11101001_{-2} = (-2)^7 + (-2)^6 + (-2)^5 + (-2)^3 + (-2)^0 =
= -128 + 64 - 32 - 8 + 1 = -103.
Перевод из системы счисления с отрицательным основанием осуществляется согласно основной формуле. Например:
Представление дробных чисел
\overline{a_n ... a_2a_1a_0,a_{-1} ... a_{-m}}_b = \sum\limits_{i = -m}^{n} a_i \cdot b^i.
Как и в случае десятичной системы счисления, в любой другой после знака запятой к числу можно приписать дробную часть. При этом цифры после запятой означают
не десятые, сотые, тысячные и т.д., а несколько иные числа. Формула для перевода в десятичную с.с.:
Пример:
110101,00101_2 = 2^5 + 2^4 + 2^2 + 2^0 + 2^{-3} + 2^{-5} =
=32 + 16 + 4 + 1 + \frac{1}{8} + \frac{1}{32} = 53\frac{5}{32} = 53,15625.
Представление дробных чисел (2)
1. Переводим в нужную с.с. целую часть стандартным способом.
2. Перевод дробной части числа из десятичной с.с. в другую выполняется последовательным умножением дробной части на основание системы счисления в которую необходимо перевести, пока дробная часть не станет равна 0.
3. Полученные целые части произведений выразить цифрами алфавита новой системы счисления и записать дробную часть числа в новой системе счисления начиная с целой части первого произведения.
180{,}65625_{10} \rightarrow x_{4}
Целая часть:
180_{10} = 3210_{4}
Дробная часть:
0{,}65625
2{,}625
4
\times
2{,}{\text{ }}5
2{,}{\text{ }}0
4
4
\times
\times
\Rightarrow 0{,}65625_{10} = 0{,}222_4
\Rightarrow 180{,}65625_{10} = 3210{,}222_{4}
* Многие дробные числа нельзя представить в виде конечных двоичных дробей. Для их точного хранения требуется бесконечное число разрядов.
Алгоритм перевода из десятичной c.с. в любую другую:
Задачи
1. Перевести числа в указанную сисстему счисления:
125_7 \rightarrow x_{4}
1. Перевести числа в указанную сисстему счисления:
а)
б)
в)
г)
д)
д)
е)
ж)
з)
и)
7F_{17} \rightarrow x_{7}
1001101_{2} \rightarrow x_{5}
11011011_{2} \rightarrow x_{8}
11011011_{2} \rightarrow x_{16}
23{,}43_{5} \rightarrow x_{10}
710{,}2_{8} \rightarrow x_{10}
18F{,}A_{16} \rightarrow x_{10}
11011011_{2} \rightarrow x_{16}
FR{,}R_{36} \rightarrow x_{10}
й)
к)
л)
м)
н)
11010001_{-2} \rightarrow x_{10}
323_{-4} \rightarrow x_{10}
5{,}625_{10} \rightarrow x_{2}
57{,}515625_{10} \rightarrow x_{4}
5{,}1_{8} \rightarrow x_{2}
Задачи (2)
3. В системе счисления с некоторым основанием десятичное число записывается в виде . Найдите это основание.
x
18
30
4. Запись числа в некоторой системе счисления выглядит так: . Найдите основание системы счисления .
65_8
311_{\alpha}
\alpha
2. Укажите наибольшее десятичное число, которое в шестеричной системе счисления можно записать с помощью трёх цифр.
1. Сколько существует натуральных чисел , для которых выполнено неравенство ?
11011100_2 < x < DF_{16}
x
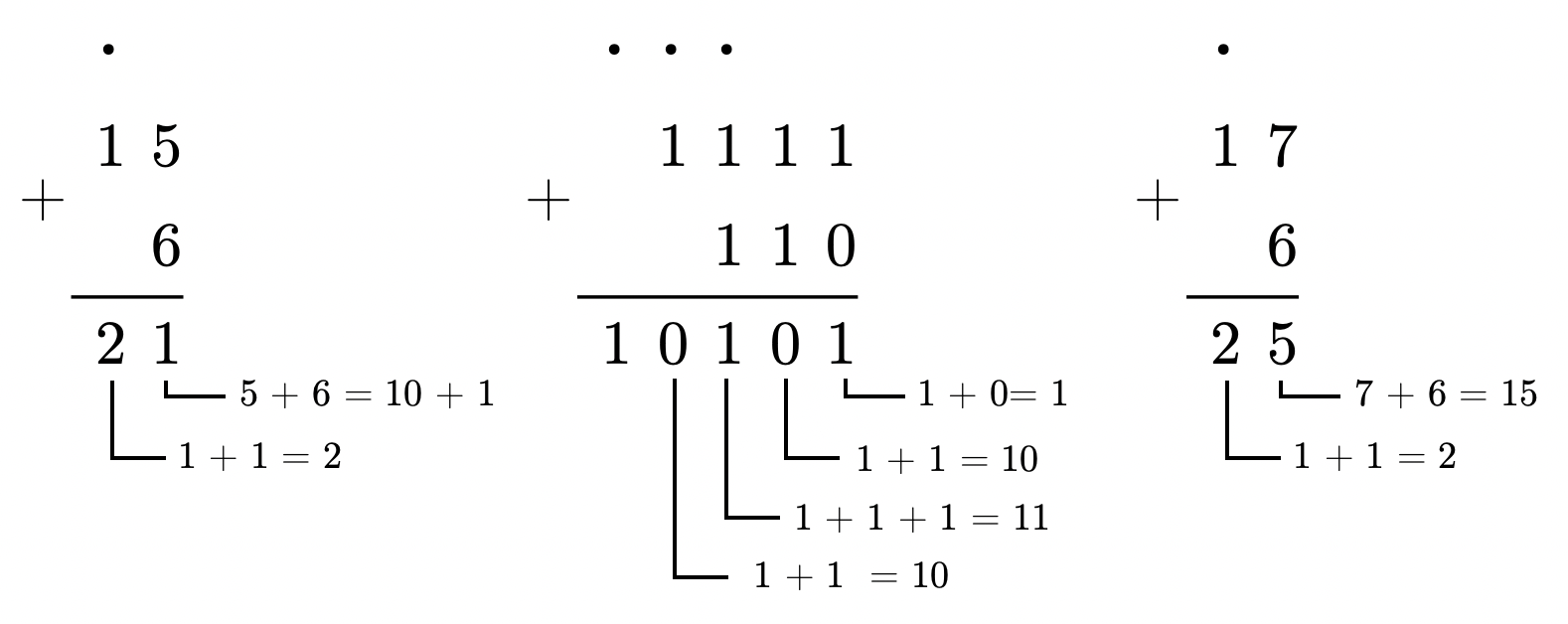
Сложение в позиционных системах счисления
Если сумма складываемых цифр больше или равна основанию системы счисления, то единица переносится в следующий слева разряд.
15_{10} + 6_{10}
1111_{2} + 110_{2}
17_{8} + 6_{8}
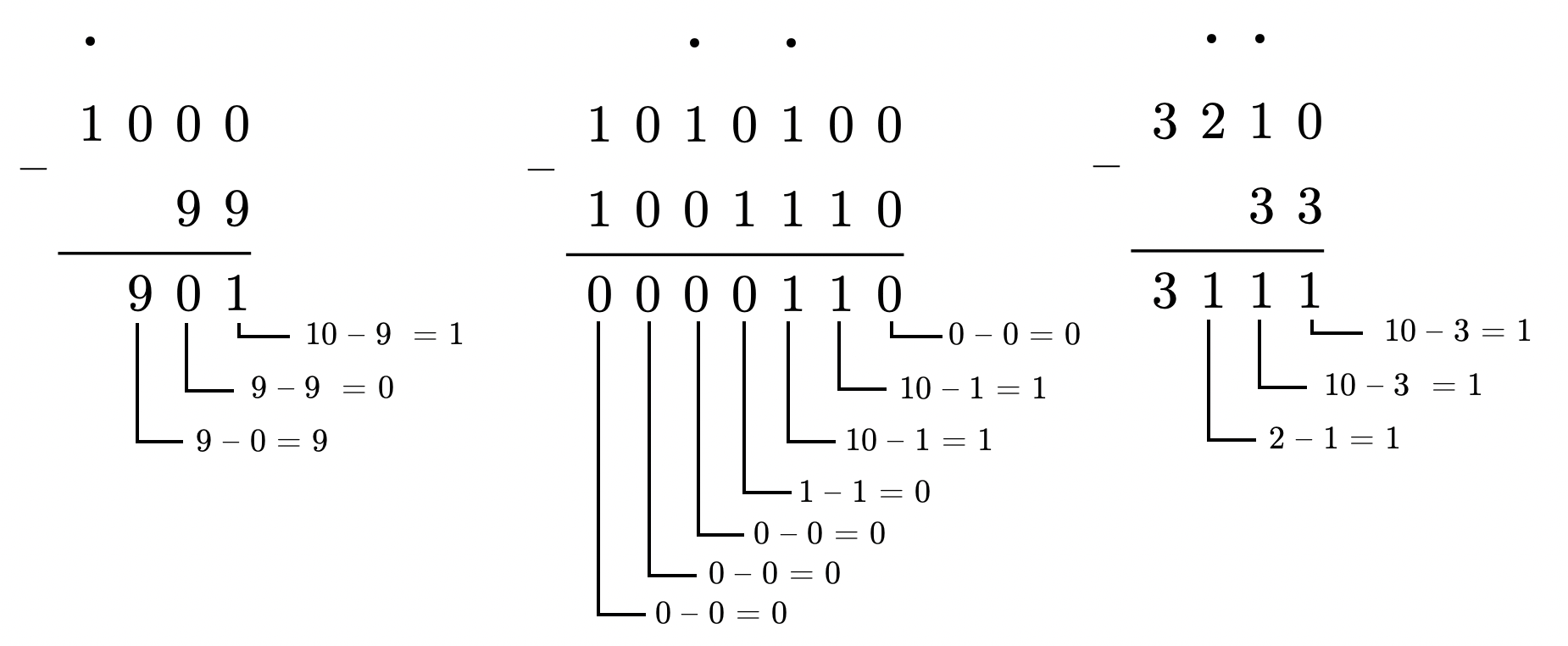
Вычитание в позиционных системах счисления
При вычитании из меньшего числа большего производится заем из старшего разряда.
1000_{10} - 99_{10}
3210_{4} - 33_{4}
1010100_{2} -
- 1001110_{2}
Последняя цифра (крайняя справа) в записи числа в системе счисления с основанием — представляет собой остаток от деления этого числа на :
Некоторые свойства (1)
b
b
7_{10} = 11\boldsymbol{1}_2 \Leftarrow 7 \texttt{ }\mathrm{mod}\texttt{ }{2} = \boldsymbol{1};
14\boldsymbol{2}_{10} \Leftarrow 142 \texttt{ } \mathrm{mod}\texttt{ }{10} = \boldsymbol{2}.
Все цифры, кроме последней (крайней справа) в записи числа в системе счисления с основанием — представляет собой значение операции деления нацело этого числа на :
Некоторые свойства (2)
b
b
\boldsymbol{14}2_{10} \Leftarrow 142 \texttt{ }\mathrm{div}\texttt{ }{10} = \boldsymbol{14};
77_{10} = \boldsymbol{100110}1_2 \Leftarrow 77 \texttt{ }\mathrm{div}\texttt{ }{2} = 38_{10} = \boldsymbol{100110}_2.
Любое десятичное число вида в системе счисления с основанием записывается как единица и нулей:
Некоторые свойства (3)
a^n
n
a^n_{10} = \overline{1{\underbrace{0...0}_{n}}}{}_a.
a
Число в системе счисления с основанием записывается как старших цифр этой системы счисления, то есть :
Некоторые свойства (4)
a^n - 1
n
a^n_{10} - 1_{10} = \overline{{\underbrace{\{a-1\}\{a-1\} ... \{a-1\}}_{n}}}{}_a.
a
a - 1
Число в системе счисления с основанием записывается как (при ) старших цифр этой системы счисления, то есть , и нулей:
Некоторые свойства (5)
a^n - a^m
n > m
a^n_{10} - a^m_{10} = \overline{{\underbrace{\{a-1\}\{a-1\} ... \{a-1\}}_{n - m}}{\underbrace{0...0}_{m}}}{}_a.
a
n-m
a-1
m
Задачи (1)
1. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие , запись которых в двоичной системе счисления оканчивается на .
2. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие , запись которых в четверичной системе счисления оканчивается на .
4. Укажите через запятую в порядке возрастания все основания систем счисления, в котором запись числа оканчивается на .
3. В системе счисления с основанием запись числа оканчивается на , а запись числа — на . Чему равно число ?
25
101
25
11
79_{10}
2
n
111_{10}
1
n
23
2
Задачи (2)
5. Значение выражения записали в системе счисления с основанием . Сколько цифр содержится в этой записи?
3
9^{12} + 3^8 - 3
2
6. Значение выражения записали в системе счисления с основанием . Сколько цифр содержится в этой записи?
6
36^7 + 6^{19} - 18
0
7. Значение выражения записали в системе счисления с основанием . Сколько цифр содержится в этой записи?
7
6 \cdot 343^5 + 5 \cdot 49^7 - 50
6
Какова последняя цифра записи числа ?
7^{2019}
Какова последняя цифра записи числа в девятеричной системе счисления?
7^{2019}
1. Системы счисления
By vkrysanov320
