Distributed and Parallel High Utility Sequential Pattern Mining
吳易倫
Yi-Lun Wu
Problem Description
Definition:
-
Item: id[price]
- 1[4], 2[3]
-
Itemset: a set of item
- {1[4], 2[9], 3[2]}
-
Sequence: a sequence of itemset
- ({1[4], 2[9]}, {2[3], 3[3], 4[1]}, {4[4]})
Problem Description cont.
-
Itemset: a set of item
- {1[4], 2[9], 3[2]}
- sorted in item id w.l.o.g.
-
Sequence: a sequence of itemset
- ({1[4], 2[9]}, {2[3], 3[3], 4[1]}, {4[4]})
- order of itemsets in sequence is meaningful
S_1=(\{1[4], 2[9]\}, \{2[3], 3[3], 4[1]\}, \{4[4]\})
P_1=(\{1, 2\},
\{4\})
Two subsequence in are similar to
S_1
P_1
S_2=(\{1[4], 2[9]\}, \{2[3], 3[3], 4[1]\}) \sim P_1
S_3=(\{1[4], 2[9]\}, \{4[4]\}) \sim P_1
Utility(P_1,S_2)=4+9+1=14
Utility(P_1,S_3)=4+9+4=16
Utility(P_1,S_1)=Max(14,16)
Problem Description cont.
S_1,S_1,S_3,\cdots,S_n
Utility(P, Database) = \sum_{i=0}^{i=n}Utility(P,S_i)
Utility of pattern P in database:
Purpose: find all
P
s.t.
Utility(P, Database)>threshold
Problem Description cont.
Find Utility of Patterns in a Sequence
-
USpan algorithm
-
Concept: Brute Force
-
Strategy: Depth First Search
-
Each node in space search tree represents a pattern state
-
Calculating utility of next pattern is based on previous utility
-
-
S_1=(\{1[4], 2[9]\}, \{1[3], 3[1], 4[2]\}, \{3[10]\})
\{4,3\}
\{9\}
\{1,10\}
(\{3\})
(\{1\})
(\{2\})
\{13\}
(\{1,2\})
\{5,14,13\}
(\{1\},\{3\})
\{4\}
\{2\}
(\{4\})
\cdots\cdots
\{7\}
(\{1\},\{3,4\})
\{15\}
(\{1\},\{3\},\{3\})
\{0\}
(\{\})
Concat-2
Concat-3
Concat-3
Concat-4
Concat-3
No downward closure property
Concat-1
(\{1,3\})
USpan Algorithm
Algorithm in Spark
RDD1
USpan
USpan
USpan
USpan
Global Filter
Local Filter
Maintain all Local High Utility Pattern in RDD2
Calculate Global Utility of each pattern
Output
Similar to USpan
Alpha-Beta pruning in DFS
Experimental Results
Candidates
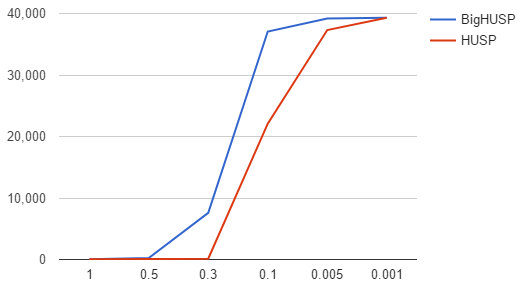
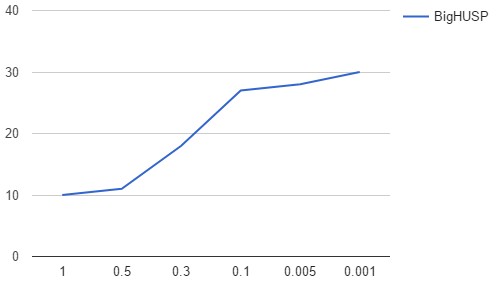
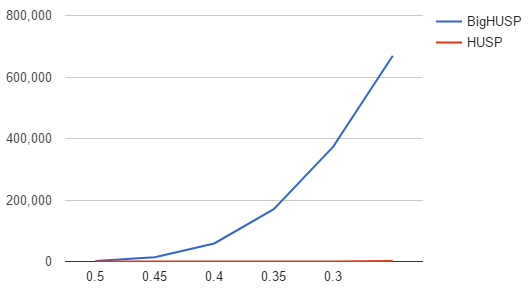
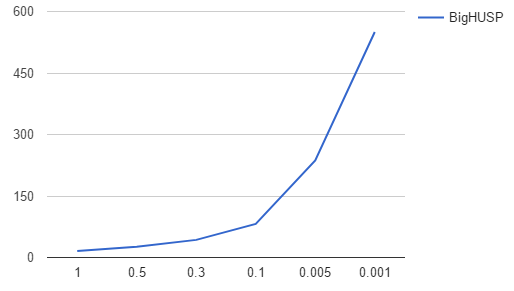
Candidates
Time(s)
Time(s)
Threshold(%)
Threshold(%)
Threshold(%)
Threshold(%)
Dataset1 1000 sequence
Dataset2 100 sequence
Extra Results
-
Algorithm(named PG-HUSP mining) which check whether a pattern is Global High Utility Pattern is surprisingly fast
- PG-HUSP
-
My algorithm(Dynamic programming)
-
-
- PG-HUSP
worst\ case:O(n^m)
n = length\ of\ sequence, m = length\ of\ pattern
worst\ case:O(n\times m)
n = length\ of\ sequence, m = length\ of\ pattern
depend\ on\ the\ number\ of\ subsequence
average:\Theta (n\times m)
-
One of Global filter does not work
Extra Results cont.
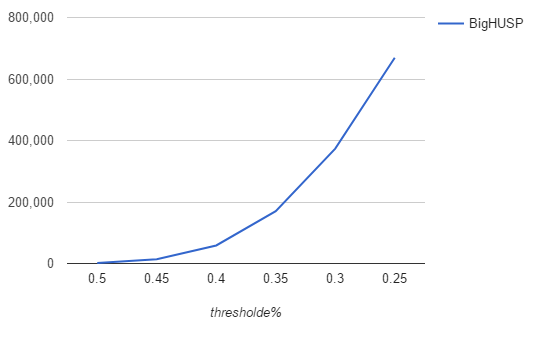
Remove filter
Apply filter
=
Q&A
Project at
https://github.com/w86763777/ParallelizedUSpan
CCBDA Final Presentation
By w86763777
CCBDA Final Presentation
paper: http://www.eecs.yorku.ca/research/techreports/2016/EECS-2016-03.pdf
