二分圖
About Bipartite Graph
— 225 陳澔樂
Index
其他資源
定義
〞
什麼是二分圖？
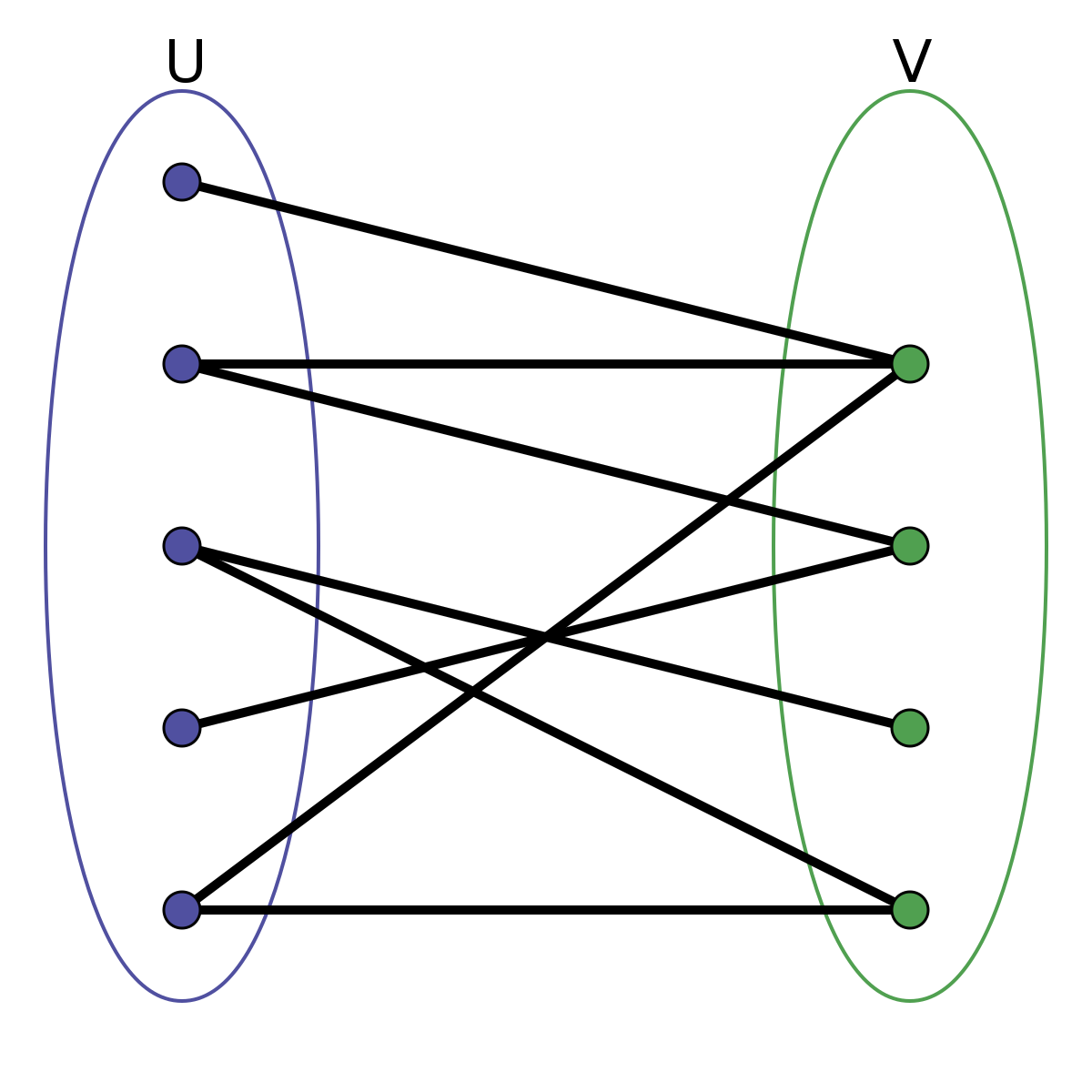
一張圖如果可以分成兩團，且每一團裡面都互不相連，他就是二分圖
- 一張圖是 2-colorable
- 一張圖不存在奇環
等價於
作一次dfs，將圖塗色
如果需要三種以上顏色的話
就不是，不然就是
檢查二分圖
Code
bool dfs(int cur) {
for(auto e : edge[cur]){
if(!color[e]){
color[e] = 3-color[cur];
if(!dfs(e)) return 0;
}else if(color[e]==color[cur]){
return 0;
}
}
return 1;
}檢查二分圖
動態加邊，強迫在線
DSU?
怎麼作？
把一個點拆成兩個點
匹配.first
一個匹配是一個圖中邊的集合P
使得每兩條在P的邊都沒有共同頂點
定義
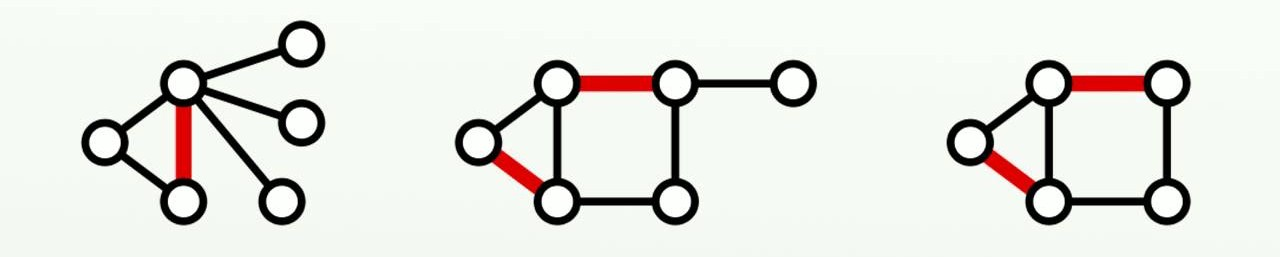
- 最大匹配：所有可能匹配中邊數最多
- 完美匹配：所有點都在匹配之中（一定是最大）
- 最大權匹配：所有匹配中邊權重和最大的
- 最大權最大匹配：所有最大匹配中邊權重和最大
- 最大權完美匹配：有完美匹配的最大全最大匹配
名詞
- 最大權最大匹配 →最大權匹配
- 最大權匹配 →最大權最大匹配
互相轉換
：為什麼要二分圖
二分圖最大匹配
因為我也不會一般圖
因為這堂課叫做二分圖
二分圖很有用阿
：這個東西可以用 flow 做吧
二分圖最大匹配
對
算法先備知識：
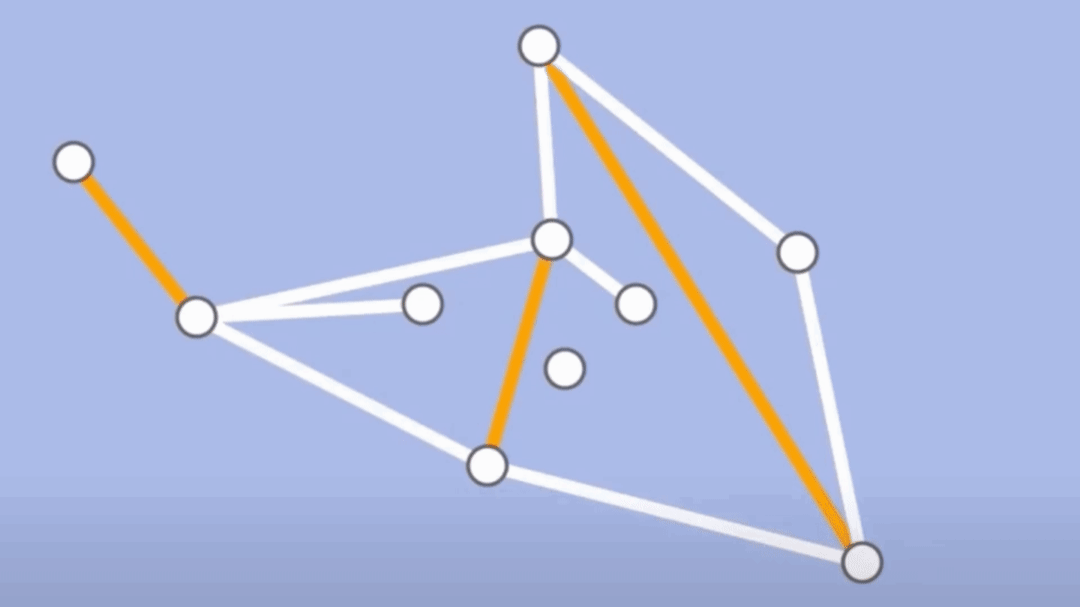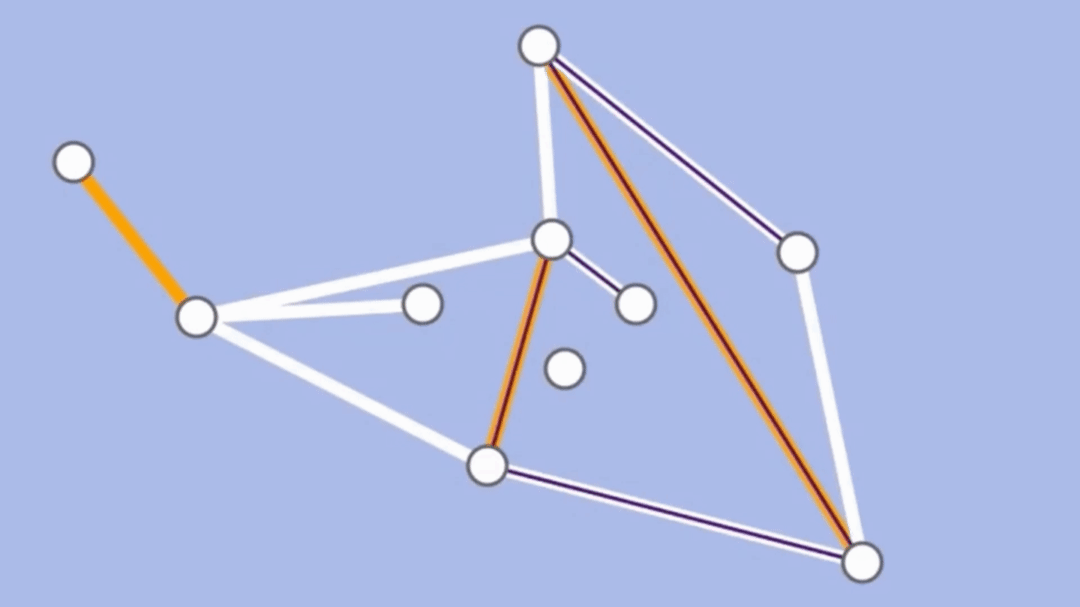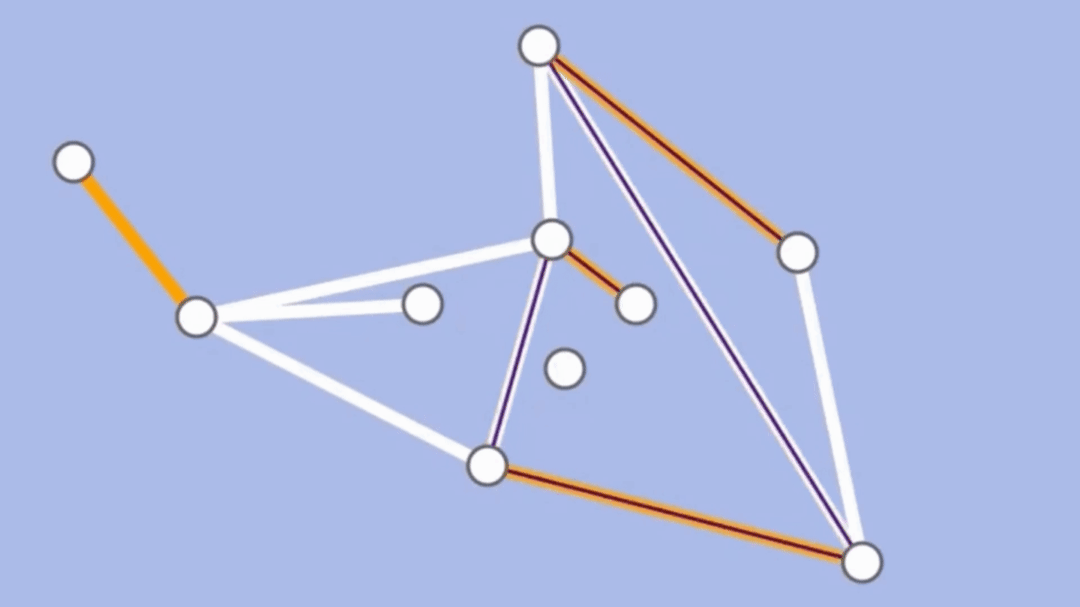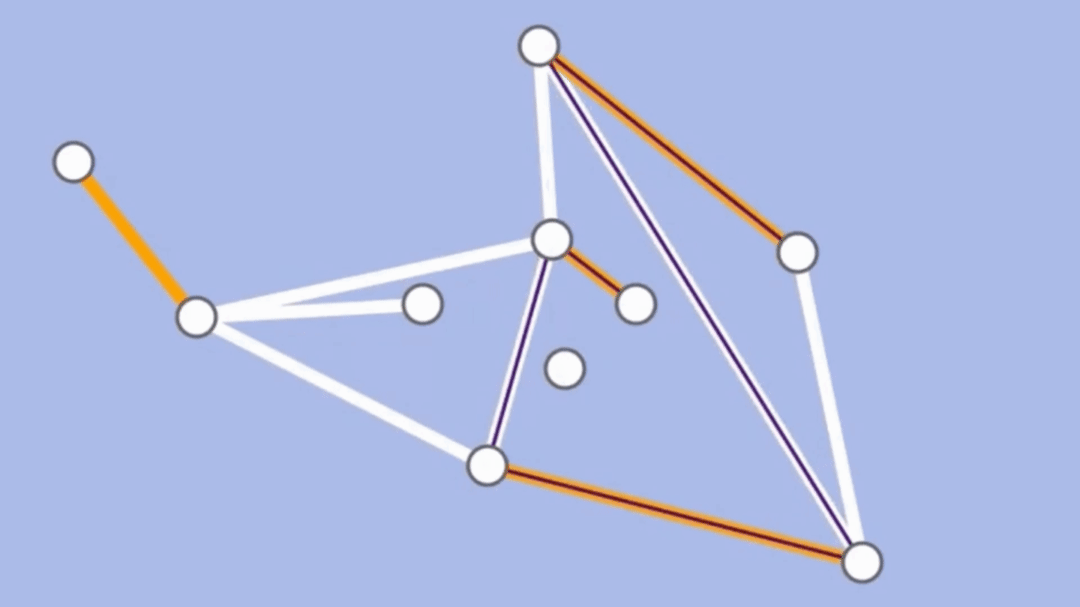
- 交替路徑：從一個未匹配點出發，依次經過非匹配邊、匹配邊、非匹配邊…形成的路徑
- 擴充路徑：一個交替路徑最後是未匹配點的路徑
二分圖最大匹配
算法先備知識：
Berge's Theorem:
若有一個匹配沒有一條擴增路徑，他一定是最大匹配
二分圖最大匹配
算法先備知識：
Berge's Theorem:
證明：
考慮反例 有一個匹配沒有擴增路徑，且他不是最大匹配 叫他 S 使其中一個最大匹配為 B
將S中的邊和B中的邊取出來 形成一個新的圖P(只有S和B中的邊的圖，節點不變) p.s. 圖p可能不是連通的
我們把原本在S裡面的邊塗黑 B中的塗白，在S和B中的塗灰 我們需要證明白邊不會比黑邊多
二分圖最大匹配
分開討論區塊情況
- 若有一個灰邊 這個灰邊連結的節點在P 中一定是和其他節點隔離(因為不會有其他邊(匹配性質))→不用管他(白==黑)
- 若有一個節點沒有任何邊，不用管他(白==黑==0)
剩下的情況是只有白邊和黑邊的很多個區域
他可以長什麼樣子？
二分圖最大匹配
性質1 P中沒有一個節點的度數超過2
沒有一個點可以有兩個同一種顏色的邊，又只有兩種顏色
根據性質1 ，區域只能長兩種樣子：
第一種是白黑交替的直鏈，第二種是白黑交替環
如果是白黑交替環→環的邊數一定是偶數(需要交替) → (白==黑)
如果是直鏈那又有三種情況→ 頭尾都是黑，頭尾都是白，頭尾不同色
- 若頭尾不同色 → 白==黑
- 若頭尾都是黑→ 黑>白(白邊沒有比黑邊多)
- 如果頭尾都是白→此區塊在原本的匹配S中是一個擴增路徑(開頭在未匹配邊，結尾在未匹配邊) → 不符合假設
所以白邊不比黑邊多，證畢
二分圖最大匹配
所以我們知道，沒有擴充路徑就是最大匹配了，那如何設計演算法？
二分圖最大匹配
一直找擴充路徑直到找不到為止
演算法
二分圖最大匹配
bool vis[MAXN2];/*是否走訪過*/
bool dfs(int u){//是否有擴增路徑
for(size_t i=0;i<g[u].size();++i){
int v=g[u][i];
if(vis[v])continue;
vis[v]=1;
if(match[v]==-1||dfs(match[v])){//如果過去的那個點沒有匹配邊或從那個點的匹配點出發有擴增路徑就有
match[v]=u;
return 1;
}
}
return 0;
}
演算法
二分圖最大匹配
int ans=0;
fill(match,match+n2,-1);
for(int i=0;i<n1;++i){
fill(vis,vis+n2,0);
if(dfs(i))++ans;
}
return ans;
演算法
二分圖最大匹配
複雜度
\Omicron(VE)
一般圖最大匹配
我一開始就說我不會了
一些性質
- 點(邊)覆蓋 (Vertex/Edge cover): 圖上的一個點(邊)集使得所有邊(點)都和該集合的點(邊)相鄰
- (點)獨立集(Independent Set):圖上的一個點集II使得II內任兩個點不相鄰。 (邊獨立集就是指匹配)
名詞定義
對於所有圖來說
|最大匹配| + |最小邊覆蓋|=|最小點覆蓋| + |最大獨立集|= |V|
性質
對於二分圖來說
|最大匹配| =|最小點覆蓋|
|最大匹配|=|最小點覆蓋|
|最小點覆蓋|\geq|最大匹配|
每一條邊都要被覆蓋=>所有匹配邊都至少貢獻1點
然後我們可以構造出一個和最大匹配一樣大的最小點覆蓋
|最大匹配|=|最小點覆蓋|
將二分圖分成L和R
從L的未匹配點開始走交替路徑DFS
選碰不到的在L的點和碰得到的在R的點
形成點覆蓋
這樣的交替路徑會是
L->未匹配邊->R->匹配邊->L.....
這個點集合大小和最大匹配一樣
因為L中選的點都有匹配(不然會從他開始DFS，會碰到)
R中選的點都有匹配(不然會有擴充路徑)
兩者的匹配邊不會重複(不然L中的點會被DFS碰到)
|最大匹配|=|最小點覆蓋|
這個東西真的是點覆蓋
因為假設有一邊(x,y)使得x和y都沒被選到
這個邊不能是匹配邊
(因為上一頁證明所有匹配邊都洽有一個點被選到)
也不能是非匹配邊
(因為這代表x可以走到y)
表示這個邊不存在
|最大匹配|=|最小點覆蓋|
所以我們知道他真的是點覆蓋且大小和最大匹配一樣
又最小點覆蓋沒辦法小於最大匹配
這個東西是最小點覆蓋
證畢
|最大匹配|=|最小點覆蓋|
匹配.second
二分圖最大權匹配
KM算法
二分圖最大權匹配
KM算法
這個演算法算的是一張二分圖的最大權完美匹配
可以用前面的方法變成最大權匹配
二分圖最大權匹配
KM算法
定義
頂標:
要用KM算法 我們要先引入頂標
將每一個點都賦予一個數值l(v)\\
使得任意邊e(u,v) \\
都滿足 l(v)+l(u)\geq w(e(u,v))\\
且l(v)+l(u)-w(e(u,v))定義為e的相對邊值
二分圖最大權匹配
KM算法
頂標
他有一個性質
任意完美匹配 P 權重和 \\都小於等於\\ 任意合法頂標和\\
\sum\limits_{e(u,v)\in P} w(e)\leq \sum\limits_{e(u,v)\in P} l(u)+l(v) = \sum\limits_{v \in V} l(v)
如果可以找到所有合法頂標和中的最小值
就可以找到最大權完美匹配
二分圖最大權匹配
KM算法
令E^\prime = \{e(u,v)\in E\space | \space l(u)+l(v)=w(e)\}\\
G^\prime 為 邊集合變成E^\prime 的 G的子圖\\
如果G^\prime 中存在完美匹配 P 則\\
\sum\limits_{e(u,v)\in P} w(e) = \sum\limits_{e(u,v)\in P} l(u)+l(v) = \sum\limits_{v \in V} l(v)
此時頂標和一定是最小值
(比他更小表示有一合法頂標方法比一個匹配權重和小)
表示G`的完美匹配為G的最大權完美匹配
將E`的邊稱為緊邊 G`稱為緊邊子圖
二分圖最大權匹配
KM算法
演算法過程
- 一開始先隨意找一個合法的頂標
- 當緊邊子圖的匹配大小<n的時候:
- 增加匹配大小
- 改變點權使其他緊邊出現。
增加匹配大小就在G′找增廣路徑就好了。
第二點要怎麼做到?
二分圖最大權匹配
KM算法
考慮剛剛最小點覆蓋的東東
我們在G`上找到最小點覆蓋
令V_L 為 L中的\text{vertex cover}\\ V_R為R中的 \text{vertex cover}\\
因為現在還不是G^\prime的完美匹配\\ 所以必定存在一種邊e(u,v)\in G,u\in L/V_L,v\in R/V_R\\
且e不是緊邊\\
把所有這種e的相對邊值的最小值\Delta找出來
二分圖最大權匹配
KM算法
把L/V_L的點的頂標都-\Delta 所有 V_R的點的頂標都+\Delta\\
已經是緊邊的邊會保持是緊邊\\
且至少會多一條緊邊\\
繼續在新的緊邊子圖G^\prime上面找擴充路徑\\
總有一天會有G^\prime上面的完美匹配
二分圖最大權匹配
KM算法
複雜度為\\ 每次擴充路徑的O(n^2)\cdot可能要產生緊邊 O(n^2) 條\\
總共O(n^4)
二分圖最大權匹配
KM算法
可以優化到O(n^3)
或是用MCMF也是O(n³)
一般圖最大權匹配
如果我連不帶權的都不會了
你為甚麼覺得我會帶權的
題目
Thank You!
PCCORZ
資讀 二分圖
By Willy Chan
