Three Faces of Natural Deduction
Author: G. Mints
Presenter: X. Xie
What three faces?
- extracting programs from proofs (Curry-Howard isomorphism)
- rigorous human reasoning
- suitable for immediate proof search
Translations of sequent calculus into natural deduction
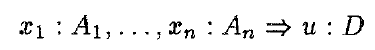
Term assignment systems that operates statements in the form of
where x1, ..., xn are variables, u is a term and A1, ..., An and D are formulas.
To find a term for formula D that encodes a proof d, which is call T(d).
Global term assignment T
Correspondence between lambda-terms and natural deductions
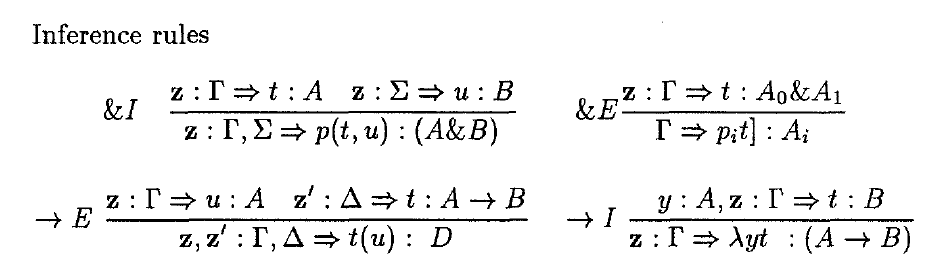
Local term assignment L
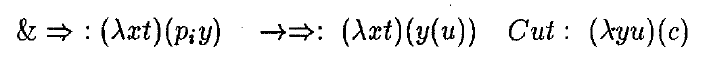
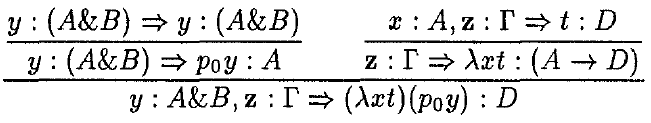
Differs only by the terms assigned to conclusions of antecedent logical rules and cut:
viewed as intertranslations between sequent system LJ and system NJ of natural deduction
Tranformation between T and L
Theorem: For every derivation d in LJ,
T(d) = \phi(\mathbf{L}'(d))
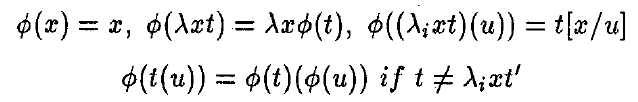
β-conversion
Add new indexed lambda-symbols λi to define L'(d).
Intuitionistic predicate logic NJi with existential instantiation
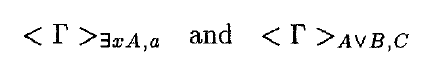
Assumptions of NJi are formulas as well as expressions of the form
Inference rules
Soundness & Completeness
Gather rules of NJi and NJ together to get NJ+, and prove the equivalence of NJ, NJi and NJ+.
Natural Deduction and Resolution
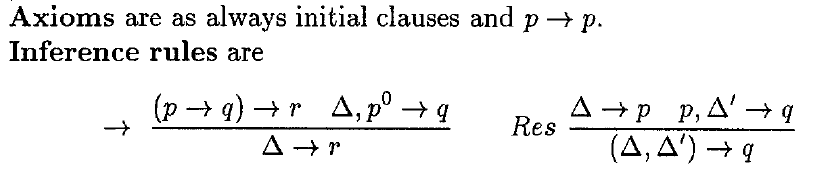
We consider system Rip
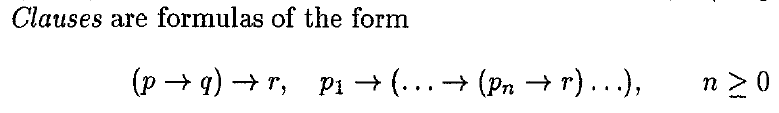
Theorem
Three Faces of Natual Deduction
By Xingyu Xie
