cog sci 131 section
week 02/28/22
by yuan meng
agenda
- mds: goal + implementation
- more on ml practices
- hw6 prompt walkthrough
multi-dimensional scaling (mds)
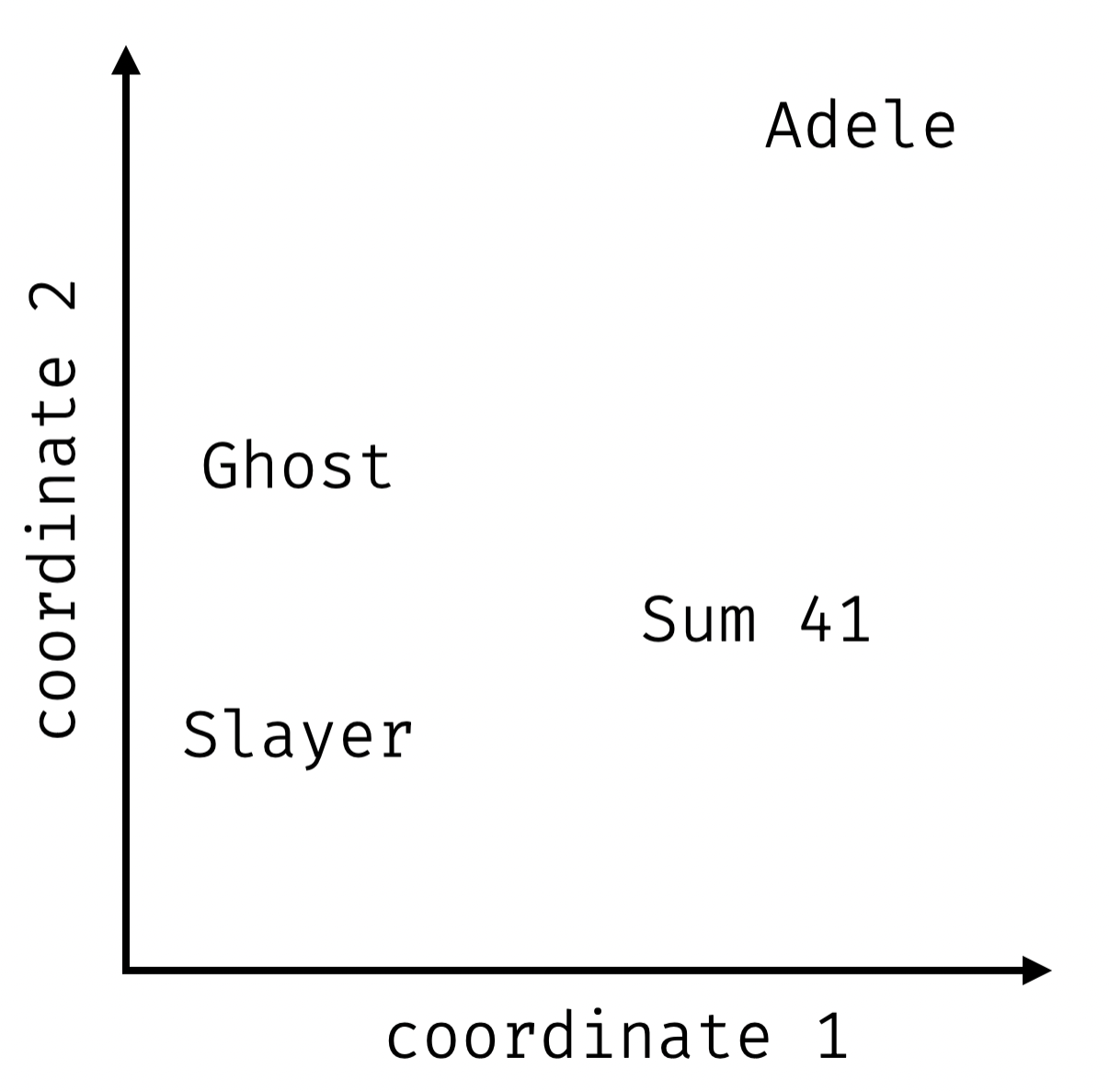
mds embeddings:
n-dimensional space
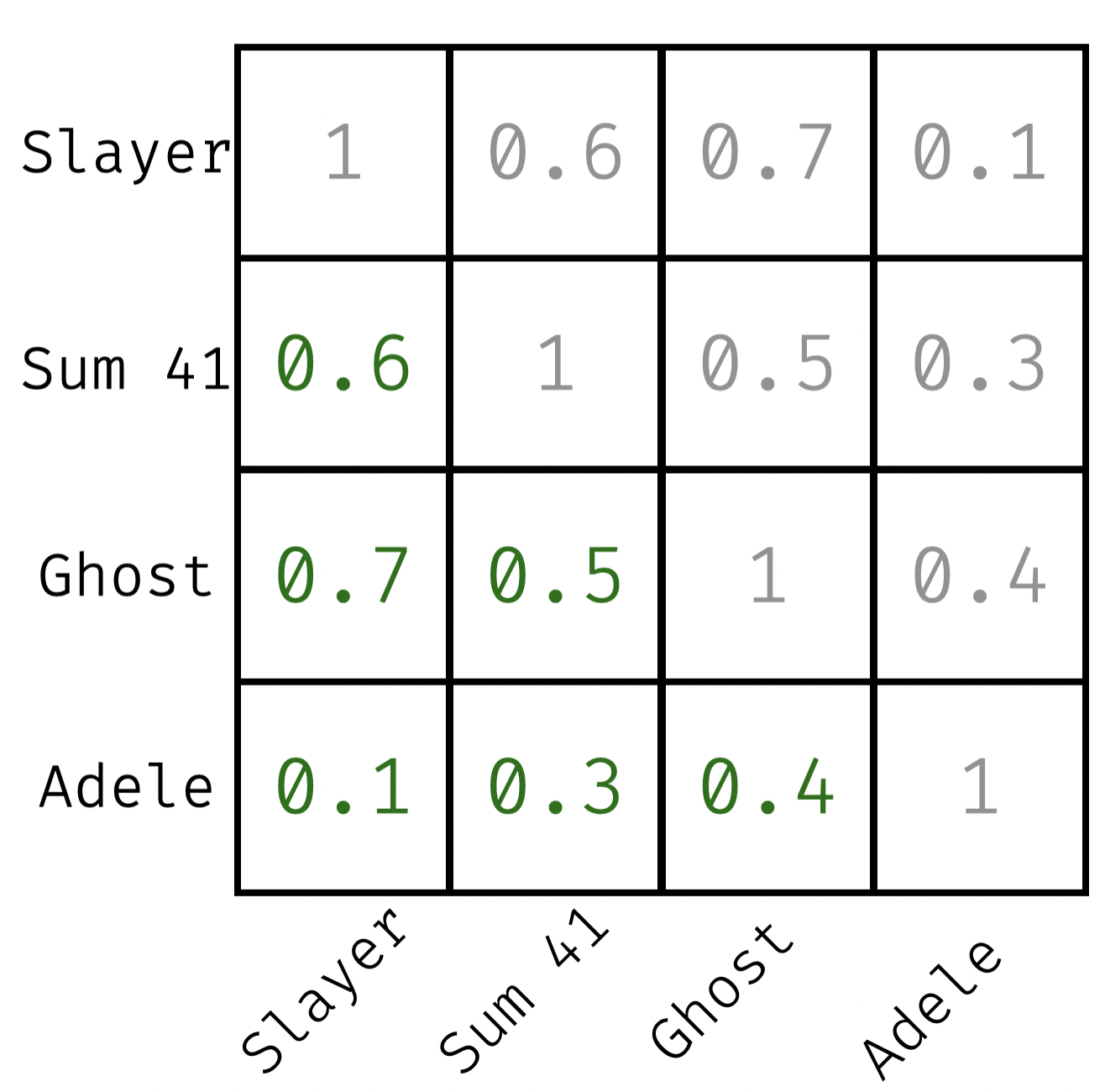
from experiments: similarity judgments
"position matrix"
Slayer: [0.2, 0.2]
Sum 41: [0.6, 0.3]
Ghost: [0.2, 0.5]
Adele: [0.7, 0.9]
need a distance function: convert similarity to distance
goal: find best mapping
any good?🤔
judged more similar 👉 closer in space
had an ml researcher invented mds, might well be called "like2vec"🤑...)
"Stress"
sum of all squared errors (psychological vs. euclidean distance) 👉 each pairwise error
- Slayer vs. Adele:
- Slayer vs. Ghost:
- Slayer vs. Sum 41:
- Sum 41 vs. Adele:
- Sum 41 vs. Ghost:
- Ghost vs. Adele:
"position matrix"
Slayer: [0.2, 0.2]
Sum 41: [0.6, 0.3]
Ghost: [0.2, 0.5]
Adele: [0.7, 0.9]
\mathrm{Stress} = \displaystyle{\sum_{i\neq j} (\psi_{ij} - dist(p_i,p_j))^2}
(1-.1) - \sqrt{(.2-.7)^2 + (.2-.9)^2} \approx .039
(1-.7) - \sqrt{(.2-.2)^2 + (.2-.5)^2} \approx 0
(1-.6) - \sqrt{(.2-.6)^2 + (.2-.3)^2} \approx -.01
(1-.3) - \sqrt{(.6-.7)^2 + (.3-.9)^2} \approx .091
(1-.5) - \sqrt{(.6-.2)^2 + (.3-.5)^2} \approx .053
(1-.4) - \sqrt{(.2-.7)^2 + (.5-.9)^2} \approx -.04
any good?🤔
square each + add together
.039 ^ 2 + 0^2 + (-.01) ^ 2 + .091 ^ 2 + .05 ^ 2 + (-.04) ^2 \\ \approx .014
psychological distance:
e.g., 1 - similarity
mds distance:
e.g., euclidean distance
pretty good
implement mds
"position matrix"
Slayer: [0.8, 0.3]
Sum 41: [0.2, 0.7]
Ghost: [0.7, 0.8]
Adele: [0.3, 0.3]
should be horrible
\displaystyle{\frac{\partial F}{\partial x_{ij}}(p) = \lim_{\delta \to 0} \frac{F(p_{ij} + \delta \cdot \mathbf{1}_{ij}) - F(p_{ij})}{\delta}}
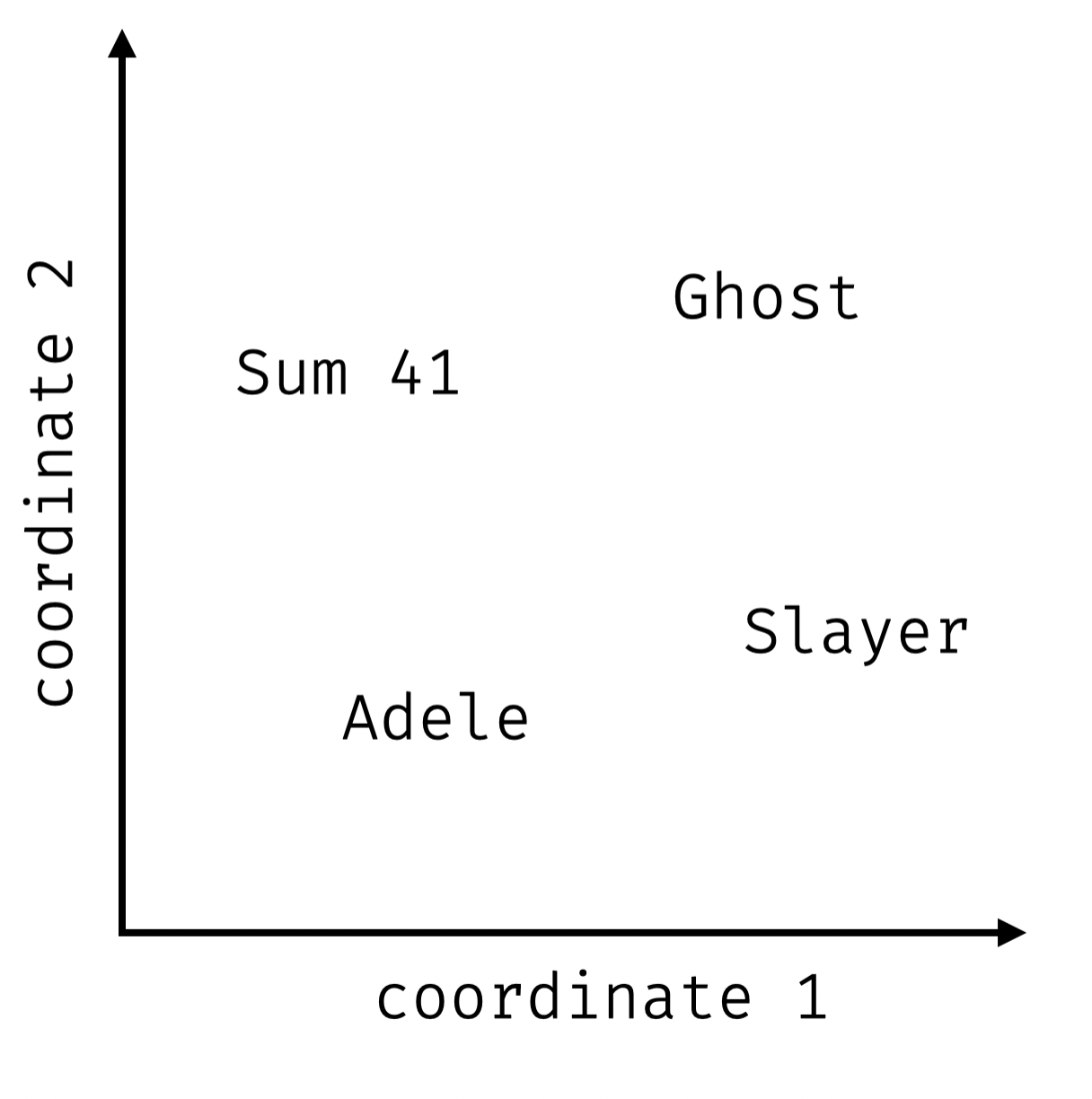
- initialization: start with random points representing each of the 4 musicians
- compute initial stress: 0.39
- compute gradients (N × 2 matrix): partial derivative wrt each point
- optimization (repeated many times): subtract each point by learning rate × its gradient
add a small value
difference between 2 Stresses
should be small
Stress
more on ml pratices (rec: cs 189)
- building blocks of an ml algorithm: e.g., mds
- loss function: how off is the model? (Stress)
- optimization criteria: when is good enough? (not specified in hw6; in practice, Stress < .001, for instance)
- optimization routine: how to improve model? (gradient descent)
- hyperparamters (don't change with training): delta (in gradients), learning rate, epochs (# of training steps), embedding dimension (dimension of each point)
- shapes of things: human judgments (N × N matrix), mds representation (N × K matrix; K = 2 in hw6), Stress (scalar), gradients (N × K matrix)
hw6 prompts
cogsci131_02_28_section
By Yuan Meng
