II Diálogos sobre-na Educação Matemática de la Universidade Estadual do Paraná
jueves 24 de junio de 2020
Ecosistemas Educativos Híbridos en la investigación en Matemática Educativa
Sergio Rubio-Pizzorno
Director de la Comunidad GeoGebra Latinoamericana


¿
¿



"El software libre es aquel que respeta tu libertad y la solidaridad social de tu comunidad”.
(Stallman, 2013)


La diferencia entre este tipo de tecnologías no está en el aspecto técnico, sino en el uso que podemos hacemos de ella, donde uno tiende más a lo individual (software privativo) y el otro más hacia lo comunitario (software libre).
- ¿Cómo se organiza la sociedad para construir conocimiento aprovechando la tecnología digital?
- ¿Qué matemáticas y cómo se aprenden éstas en la Era Digital?
Antropología
Sociología
Investigación Educativa
Matemática Educativa

VS
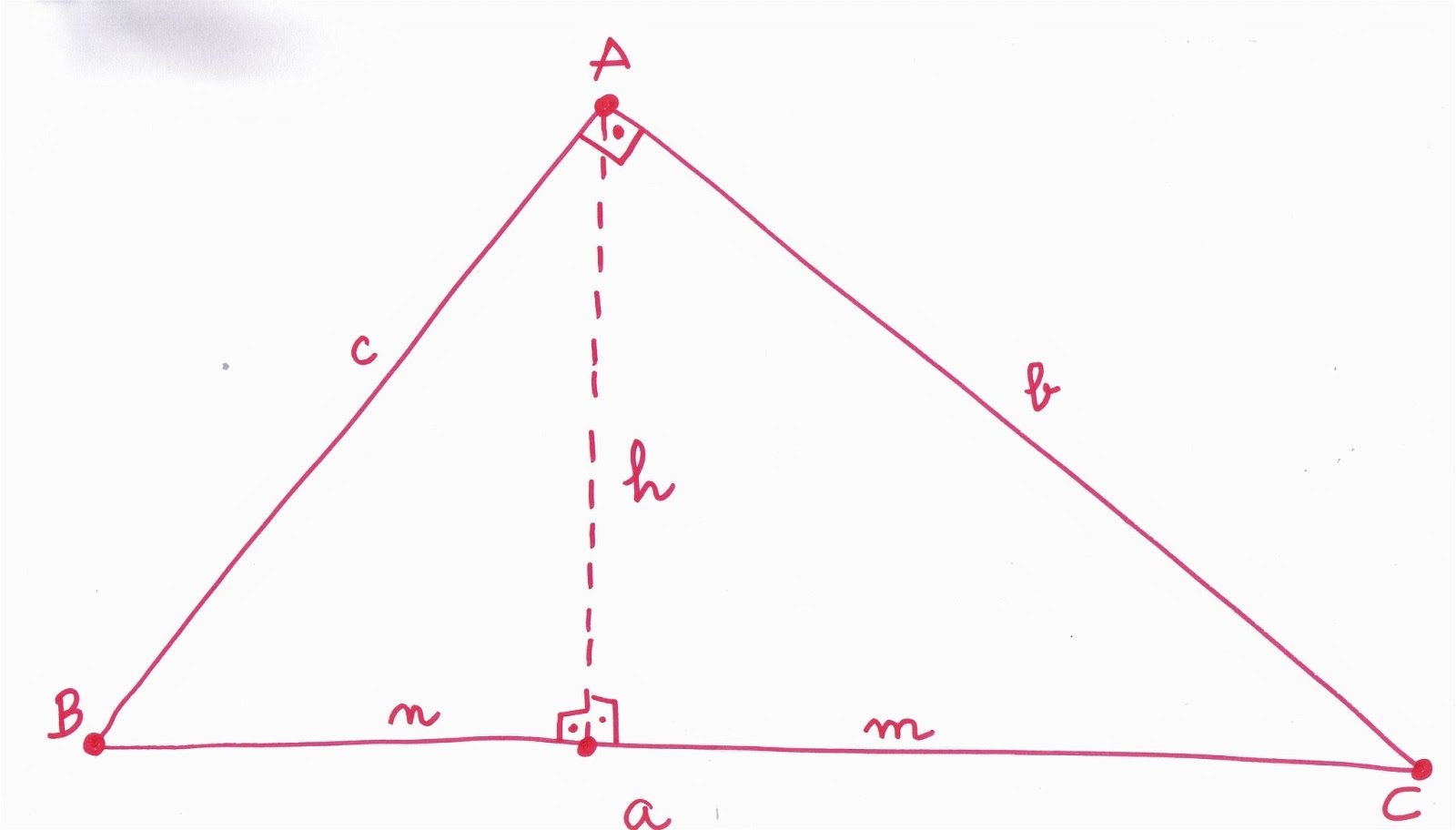
Tendencia 1: ¿Con o sin tecnología digital?
Stylianides y Stylianides, 2015; Iranzo y Fortuny, 2009; Koyuncu y otros, 2015; Hitt y otros, 2017
Tendencia 1: ¿Con o sin tecnología digital?
Iranzo, Nuria y Fortuny, Josep M (2009). La influencia conjunta del uso del GeoGebra y lápiz y papel en la adquisición de competencias del alumnado. Enseñanza de las Ciencias, 27(3), pp. 433–446.
Koyuncu, Ilhan; Akyuz, Didem y Cakiroglu, Erdinc (2015). Investigationg plane goemetry problem-solving strategies of prospective mathematics teachers in thecnology and paper-and-pencil environments. International Journal of Science and Mathematics Education, 13(4), pp. 837–862. ISSN 1571-0068. doi: 10.1007/s10763-014-9510-8.
Hitt, Fernando; Saboya, Mireille y Cortés, Carlos (2017a). Task Design in a Paper and Pencil and Technological Environment to Promote Inclusive Learning: An Example with Polygonal Numbers. En: Aldon Gilles; Fernando Hitt; Luciana Bazzini y Uwe Gellert (Eds.), Mathematics and Technology. Advances in Mathematics Education, pp. 57–74. Springer, Cham. doi: 10.1007/978-3-319-51380-5_4.
Tendencia 1: ¿Con o sin tecnología digital?
Esta tendencia de investigación y su pregunta motivadora (¿con o sin tecnología digital?), encuentran sustento en el paradigma tradicional de investigación antropológica sobre la relación entre tecnología y cultura, ya que en esta se ve a la tecnología como un periférico de las sociedades, el cual podría estar o no presente en nuestras sociedades sin mayores consecuencias.
(Santos y Díaz Cruz, 2015)
Tendencia 2: Ampliación de lo físico a lo digital


Tendencia 2: Ampliación de lo físico a lo digital
En términos teóricos, hemos notado una tendencia de los investigadores a combinar dos o más perspectivas teóricas para tener en cuenta adecuadamente sus contextos de investigación. A veces, las teorías generales del aprendizaje deben combinarse con teorías que proporcionan un enfoque más centrado en el uso de las herramientas y su papel en la enseñanza y el aprendizaje. Vemos la necesidad de articular mejor las teorías del aprendizaje con las teorías del uso de herramientas, que actualmente se hace, en su mayor parte, combinando enfoques.
(Sinclair y Yerushalmy, 2016, p. 264)
Por ejemplo: la Génesis Instrumental. Articulación entre la Ergonomía Cognitiva y TAD.
Tendencia 2: Ampliación de lo físico a lo digital
Esta tendencia de investigación encuentra su fundamento antropológico, al presentarse como una transición entre el paradigma tradicional y el moderno en la investigación antropológica sobre la relación entre tecnología y cultura.
Esta transición está marcada por comenzar a reconocer la necesidad de no trivializar el rol de la tecnología en su relación constituyente con la cultura y, en consecuencia, al estar presente en fenómenos educativos.
Tendencia 3: Característico de lo digital
Artigue (2002) llama valor pragmático de la tecnología a su potencial productivo (eficiencia, costo y campo de validez) y valor epistémico de la misma, a cómo se comprende el objeto matemático y qué preguntas genera sobre este.
Tendencia 3: Lo propio de lo digital
¿
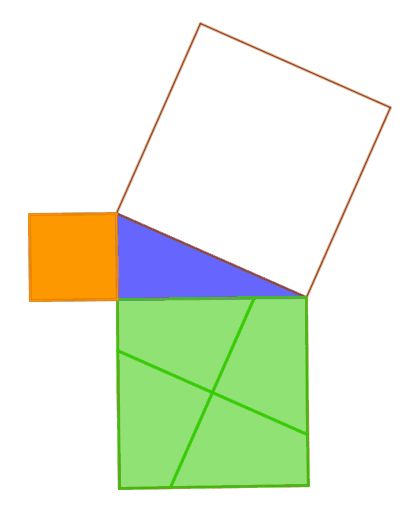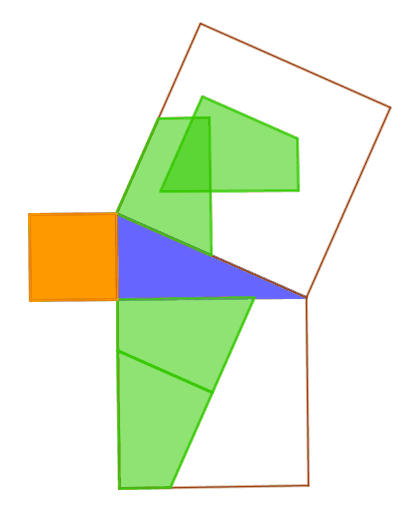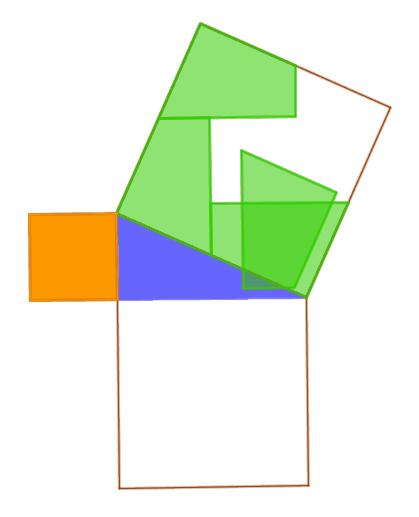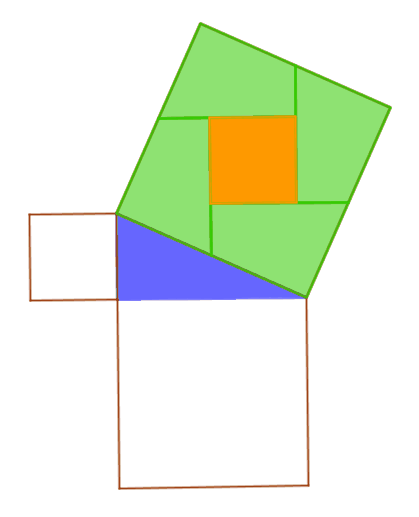
¿
Transición de lo discreto a lo continuo
Estudio de propiedades geométricas como invariantes
Tratamiento gráfico de funciones a través de variación de parámetros
Estudio de conjuntos infinitos de objetos matemáticos
Es decir, ya valoramos a la tecnología digital por sus propios méritos al estudiar matemáticas.
Tendencia 3: Lo propio de lo digital
Esta tendencia de investigación encuentra sustento en el paradigma moderno de investigación antropológica sobre el vínculo tecnología-cultura, el cual asume a la tecnología (digital) como una construcción social, cultural y simbólica en nuestras sociedades modernas y complejas. Dicho de otro modo, la tecnología es parte de la cultura y, a su vez, de la sociedad. (Santos y Díaz Cruz, 2015)
En términos sociológicos (Castells, 1999) se reconoce que el soporte material de la estructura social vigente es una hibridación entre espacios físicos y digitales.
Más allá de la dualidad física-digital
La investigación educativa propone a lo híbrido más allá de la dualidad físico-digital, en el contexto educativo.
"Visto desde una perspectiva cartográfica, podríamos plantear que se amplía el mapa de la ecología del aprendizaje. En este nuevo plano, el aprendizaje trasciende los espacios tradicionalmente delimitados para aprender. Tal como hemos señalado, el nuevo panorama del aprendizaje ha de ser en 3D y 360º, incluyendo otros territorios hasta ahora ignorados".
(Cobo y Moravec, 2011, p. 111)
Más allá de la dualidad física-digital


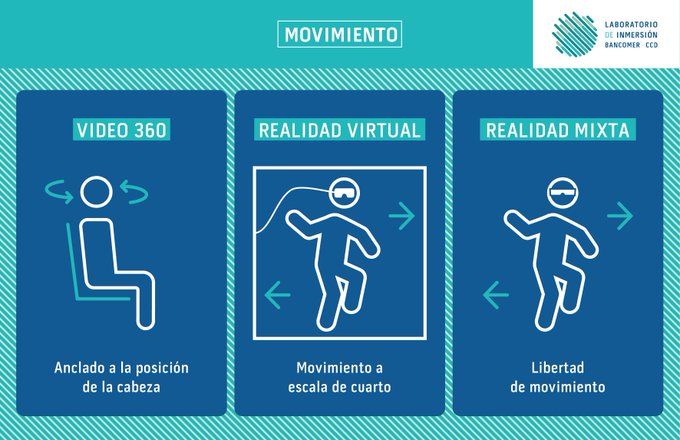
Más allá de la dualidad física-digital
Por lo tanto, se configuran ecosistemas educativo híbrido, puesto que se constituyen a partir de soportes materiales de distintas naturalezas.

Físico
Digital
Realidad Aumentada
Video 360
Realidad Virtual
Materialidad social dada por diferentes espacios
Tecnologías
Ecosistemas Educativos Híbridos

Ecosistemas Educativos Híbridos
En el campo de la Matemática Educativa, se ha reportado que la relación entre las matemáticas y la tecnología se ha dado como una mutuamente constituyente a lo largo de la historia (Moreno-Armella, Hegedus y Kaput, 2008). Esta relación se ha dado en las siguientes etapas:
- Estática inerte.
- Estática cinestésica/estética.
- Estática computacional.
- Dinámica discreta.
- Dinámica continua.
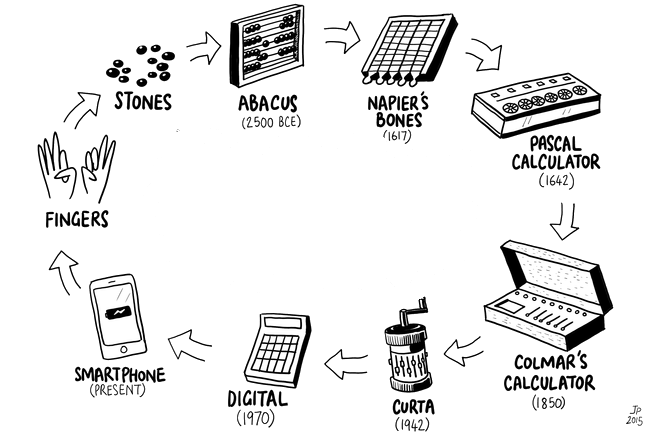
Ecosistemas Educativos Híbridos
A propósito de a relación histórica entre matemáticas y tecnología, y de la propuesta de los ecosistemas educativos híbridos, es posible declarar que los ecosistemas educativos al estudiar matemáticas pueden estar representados por diversas tecnologías (i.e. teléfonos, papel y lápiz, visor de RV, etc.).
Además, cada una de las diferentes tecnologías tendrá su valor epistémico relacionado con el estudio de alguna noción matemática en específico.
Ecosistemas Educativos Híbridos
Valor epistémico de las tecnologías: formas en que las tecnologías ayudan a comprender el objeto matemático y genera preguntas sobre este, al ser usada para desarrollar un trabajo matemático específico.
Valor pragmático de las tecnologías: potencial productivo de las tecnologías, es decir, eficiencia, costo y campo de validez.
Ecosistemas Educativos Híbridos
Uso
Forma de usar las tecnologías según el enfoque teórico (e.g. esquema de uso, técnica instrumentada)
Tecnologías
Según diferentes espacios sociales (e.g. físico, digital, realidad aumentada, video 360, realidad virtual, etc.)
Trabajo matemático
Acciones matemáticas según el enfoque teórico (e.g. resolver tareas, elaborar prácticas)
Valor pragmático y espistémico de las tecnologías
- Explorar las tecnologías disponibles, considerando los diferentes espacios sociales.
- Posicionarse en un enfoque teórico específico que permitirá determinar a qué se refiere en particular el trabajo matemático y el uso de las tecnologías.
- Indagar en el valor epistémico y pragmático de las tecnologías características de los diferentes espacios, en el desarrollo del trabajo matemático específico.
- Explorar la manera de usar coordinadamente las diferentes tecnologías para un mejor aprovechamiento de su valor pragmático y epistémico en desarrollo del trabajo matemático.
Propuesta: Ecosistemas Educativos Híbridos
Ejemplo de uso de la perspectiva de Ecosistemas Educativos Híbridos en Matemática Educativa
Ejemplo de uso de la perspectiva de Ecosistemas Educativos Híbridos en Matemática Educativa
Los niños tienden a pensar que las figuras con mayor área tienen mayor perímetro y que sólo las figuras congruentes tienen igual área (Kospentaris, Spyrou y Lappas, 2011).
¿Qué tecnología escojo?
¿Cómo puedo comenzar a usar tecnología digital?
¿Cómo logro usar la tecnología digital por sus propios méritos?

VS



¿
¿

Como investigador(a):
¿Qué te podrías haber preguntado con cada una de las tendencia de investigación?
No tengo que escoger entre diferentes tecnologías, puedo usar todas las que tengo disponible y de manera coordinada, para aprovechar su potencial al estudiar matemáticas.
Como investigador(a):
¿Qué te podrías estar preguntado al considerar la propuesta de los Ecosistemas Educativos Híbridos en tu investigación?

¡Gracias TOTALES!
Sergio Rubio-Pizzorno
Referencias
Artigue, Michèle (2002). Learning mathematics in a CAS environment: The genesis ofa reflection about instrumentation and the dialectics between technical and conceptualwork. International Journal of Computers for Mathematical Learning, 7(3), pp. 245–274. ISSN 13823892. doi: 10.1023/A:1022103903080
Cultura Colectiva (2017). Médico peruano imprime órganos en 3D y los implanta en pacientes [Video]. En facebook.com/culturacolectivanoticias/videos/1960460410848717
de Jesús, Á. (2017). Círculo y circunferencia: exploración y caracterización [Libro GeoGebra]. En geogebra.org/m/gk97hyVa
Referencias
Hohenwarter, M. (2013). Dynamic Mathematics for Everyone [Video]. Rescatado de youtu.be/Yq1eBZjz16I
LeAnn E. Neel-Romine, Sara Paul and Kathryn G. Shafer (2012). Get to Know a Circle. Mathematics Teaching in the Middle School 18(4), pp. 222-227. doi: 10.5951/mathteacmiddscho.18.4.0222
Referencias
Laborde, Colette (2002). Integration of Technology in the Design of Geometry Tasks with Cabri-Geometry. International Journal of Computers for Mathematical Learning, 6(3), pp. 283–317. ISSN 13823892. doi: 10.1023/A:1013309728825
OCDE (2008). New Millennium Learners Initial findings on the effects of digital technologies on school-age learners. OECD/CERI International Conference “Learning in the 21st Century: Research, Innovation and Policy”. París: Organisation for Economic Co-operation and Development. Rescatado de oecd.org/site/educeri21st/40554230.pdf
Rotaeche y Montiel (2017). Aprendizaje del concepto escolar de ángulo en estudiantes mexicanos de nivel secundaria. Educación Matemática, 29(1), (pp. 171 - 199). doi: 10.24844/EM2901.07
Referencias
Rubio-Pizzorno, S. (2018). Integración digital a la práctica del docente de geometría. Tesis de Maestría no publicada. Ciudad de México, México: Centro de Investigaciones y de Estudios Avanzados (Cinvestav). doi: 10.13140/RG.2.2.15488.94728/1
Rubio-Pizzorno, S.; Farfán-Cera, C. y Montiel, G. (2017). Estrategia de planeación para el trabajo con profesores, integrando tecnología digital. En D. Cobos Sanchiz; E. López-Meneses; A. H. Martín Padilla; L. Molina-García y A. Jaén Martínez (Eds.), INNOVAGOGÍA 2016. III Congreso Internacional sobre Innovación Pedagógica y Praxis Educativa. Libro de Actas. (pp. 1069 - 1077). AFOE Formacion: Sevilla, España. ISBN: 978-84-608-8348-7.
Referencias
Rubio-Pizzorno, S. y Montiel, G. (2017). Geometría dinámica como actualización didáctica de la evolución conceptual de la geometría. En P. Perry (Ed.), Encuentro de Geometría y sus Aplicaciones, 23 (pp. 143-148). Bogotá, Colombia: Universidad Pedagógica Nacional. Rescatado de www.encuentrogeometria.com/Documents/2017Memorias.pdf
Rubio-Pizzorno, S. y Montiel, G. (2017a). Consideraciones epistémicas sobre los objetos geométricos en ambientes de geometría dinámica. Análisis inicial. En L. A. Serna (Ed.), Acta Latinoamericana de Matemática Educativa, 30, (pp. 1505 - 1514). Ciudad de México, México: Comité Latinoamericano de Matemática Educativa.
Referencias
Rubio-Pizzorno, S. y Montiel, G. (2017b). Geometría dinámica como actualización didáctica de la evolución conceptual de la geometría. En P. Perry (Ed.), 23 Encuentro de Geometría y sus Aplicaciones (pp. 143 - 148). Bogotá, Colombia: Universidad Pedagógica Nacional. ISSN: 2346-0539.
Rubio-Pizzorno, S., Cruz-Márquez, G. y Montiel Espinosa, G. (2018). Trabajo geométrico, con atención en el carácter dinámico de la geometría y su proceso de construcción: análisis inicial. En L. A. Serna y D. Páges (Eds.), Acta Latinoamericana de Matemática Educativa, 31(2), (pp. 1139-1146). Ciudad de México, México: Comité Latinoamericano de Matemática Educativa. ISSN: 2448-6469.
Serres, Michel. (2013). Pulgarcita. Fondo de Cultura Económica, Buenos Aires, Argentina.
Créditos
Estudiar matemáticas en la Era Digital: Ecosistemas educativos híbridos y el rol de GeoGebra por Sergio Rubio-Pizzorno se distribuye bajo una Licencia Creative Commons Atribución-NoComercial 4.0 Internacional.
Basada en una obra en https://slides.com/zergiorubio/2019-charla-uat .
BY
NC
Ecosistemas Educativos Híbridos en la investigación en Matemática Educativa
By Sergio Rubio-Pizzorno
Ecosistemas Educativos Híbridos en la investigación en Matemática Educativa
[jueves-25-junio-2020] Presentación sobre "Ecosistemas Educativos Híbridos en la investigación en Matemática Educativa" como parte de la mesa de discusión "Bases teóricas em pesquisas abordando tecnologia na educaçao matemática", organizada por el PROGRAMA DE PÓS-GRADUAÇÃO EM EDUCAÇÃO MATEMÁTICA – PRPGEM, Brasil.
- 989







