What's in a Prior?
Learned Proximal Networks for Inverse Problems
Zhenghan Fang
CIS Retreat, December 8, 2023
Measure
Inversion
x
y
A
y=Ax+v
Inverse Problems
- \(A\): Linear forward operator
- ill-posed
A
Inverse Problem in Neuroimaging
x
Susceptibility Tensor Images
Dipole Inversion
Dipole Convolution
☹ Time-consuming
- Requires >6 orientations
Phase measurements at multiple head orientations
Phase measurements at multiple head orientations
y
- Deep unrolling, Plug-and-play
- Use information of physics model
- Adaptive to \(A\)
\min_x \|y - Ax \|_2^2 + R(x)
Regularizer
Classical Method
- Not sufficient for few orientations
Learned Proximal
\hat{x}_{k+1} = \mathrm{prox}_{\eta R}(\hat{x}_k - \eta A^H(A\hat{x}_k - y))
Proximal Operator
\hat{x}_{k+1} = {\color{orange} f_\theta}(\hat{x}_k - \eta A^H(A\hat{x}_k - y)) \\
Train \(f: X \to Y \) on \(\mathcal{D} = (x_i, y_i)_{i=1}^N\)
Vanilla Neural Network
- Not Adaptable to \(A\)
\(\hat{x} = {\color{orange} f_\theta}(y)\)
Learned Proximal for Inverse Problems
\(\mathrm{prox}_{\eta R} (z) = \arg\min_u \tfrac{1}{2} \|u-z\|_2^2 + \eta R(u)\)
Ground-Truth
STIimag
[Li et al.]
MMSR
[Li and Van Zijl]
aSTI+
[Shi et al.]
DeepSTI
(ours)
[1] Li et al, NMRB 2017; [2] Li and van Zijl, MRM, 2014;
[3] Cao et al., MRM, 2021; [4] Shi et al., IEEE JBHI, 2022
[5] Fang et al. Medical Image Analysis, 2023
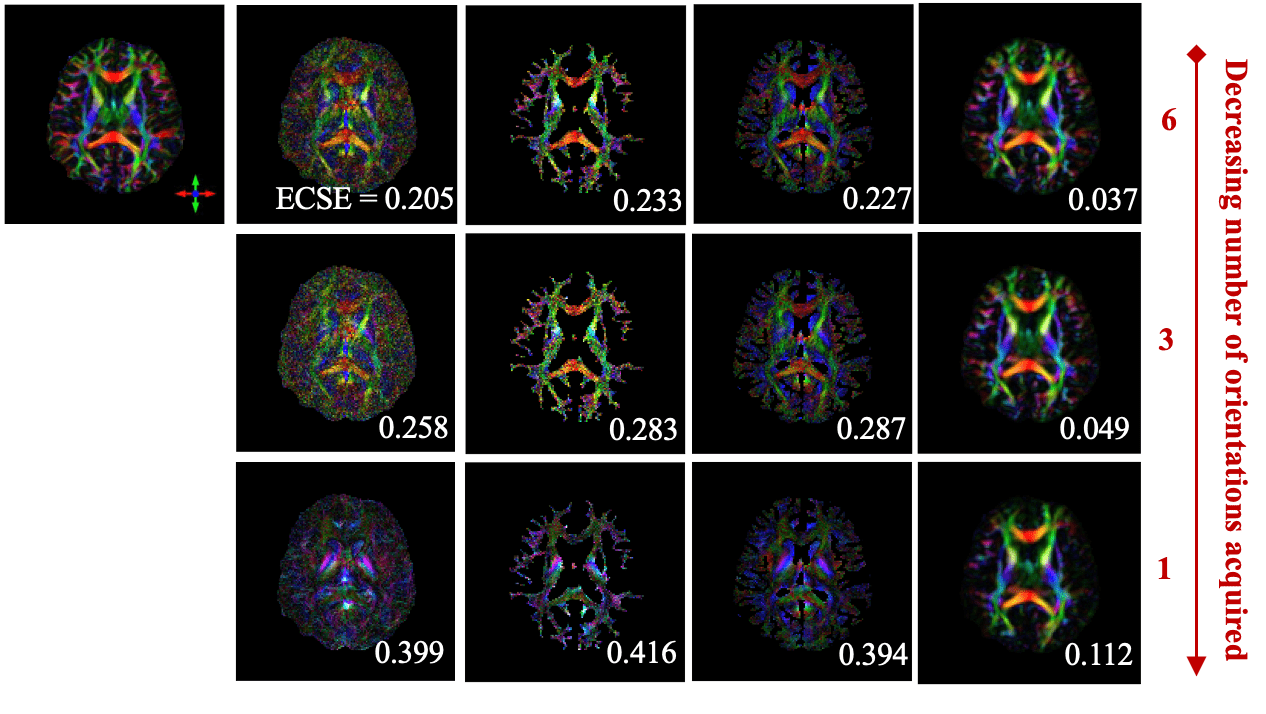
Simulation Results
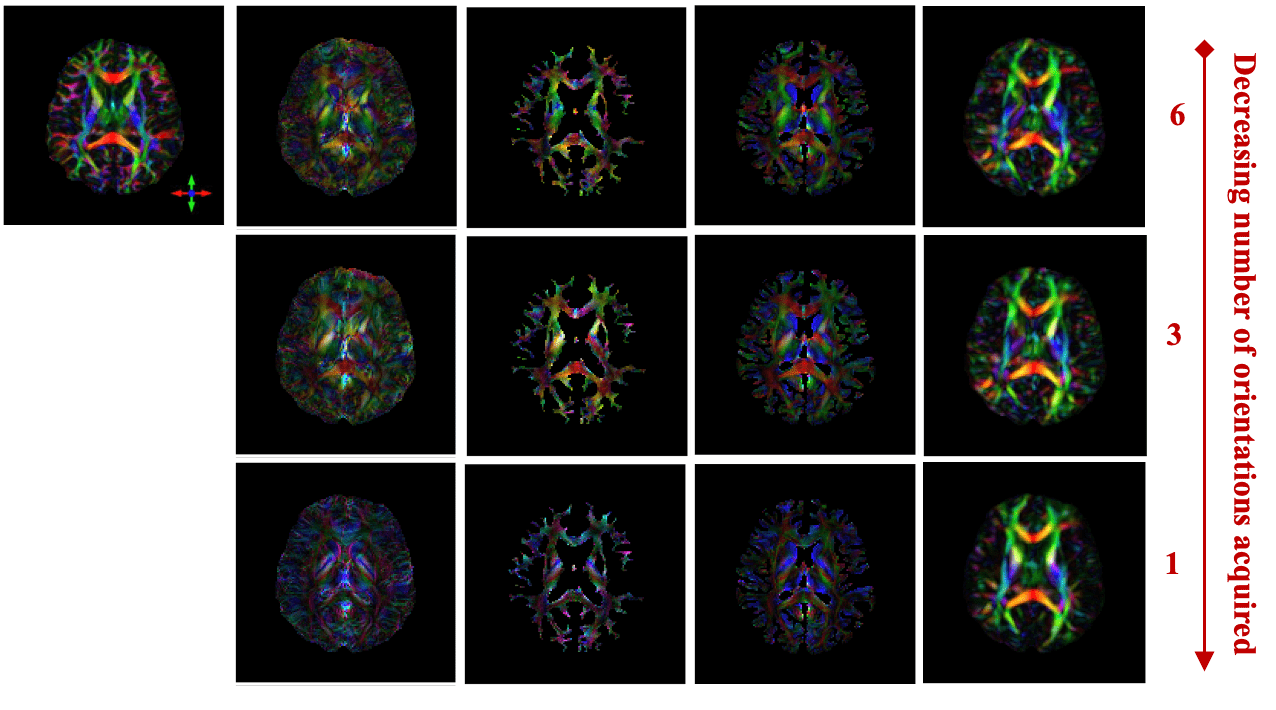
In Vivo Results
DTI
STIimag
[Li et al.]
MMSR
[Li and Van Zijl]
aSTI+
[Shi et al.]
DeepSTI
(ours)
[1] Li et al, NMRB 2017; [2] Li and van Zijl, MRM, 2014;
[3] Cao et al., MRM, 2021; [4] Shi et al., IEEE JBHI, 2022
[5] Fang et al. Medical Image Analysis, 2023
- Is \(f_\theta\) actually the proximal operator of some function \(R_\theta\)?
- What is the learned regularizer \(R_\theta(x)\)?
\hat{x}_{k+1} = {\color{orange} f_\theta}(\hat{x}_k - \eta A^H(A\hat{x}_k - y)) \\
Towards Principled and Interpretable Learned Proximal Operator 👉
Characterization of proximal operators [Gribonval and Nikolova, 2020]
Let \(f : \mathcal{Y} \rightarrow \R^n\) be a continuous function.
\(f\) is a proximal operator of a function \(R:\R^n \rightarrow \R \cup \{+\infty\}\)
if and only if
there exists a convex differentiable function \(\psi\) such that \(f(y) = \nabla \psi(y)\).
- Proximal operators are gradients of convex functions
Background
Input Convex Neural Networks [Amos et al.]
Nonnegative
Learned Proximal Networks
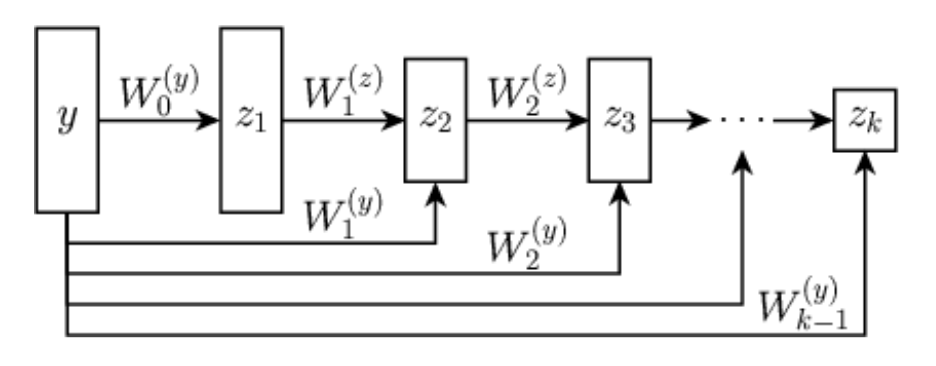
Proposition. Let \(\psi_\theta: \R^{n} \rightarrow \R\) be defined by \[z_{1} = g( \mathbf H_1 y + b_1), \quad z_{k} = g(\mathbf W_k z_{k-1} + \mathbf H_k y + b_k), \quad \psi_\theta(y) = \mathbf w^T z_{K} + b\]
with \(g\) a convex, non-decreasing nonlinear activation, and all \(\mathbf W_k\) and \(\mathbf w\) non-negative.
Let \(f_\theta = \nabla \psi_{\theta}\).
Then, there exists a function \(R_\theta\) such that \(f_\theta(y) = \mathrm{prox}_{R_\theta}(y)\).
LPN: Uncovering the Prior
Given \(f_\theta\), how can we evaluate \(R_\theta\)?
\(R(x) = \langle x, f^{-1}(x) \rangle - \frac{1}{2} \|x\|_2^2 - \psi(f^{-1}(x))\)
\[\min_y \psi_{\theta}(y) - \langle x, y \rangle\]
Optimality condition: \(\nabla \psi_\theta(y^*) = x\)
[Gribonval and Nikolova]
The minimizer provides the inverse \(f_\theta(y^*) = x\)
How to invert \(f\)? 🤔
LPN: Proximal Matching Training
\(\mathrm{prox}_{-\log p_x} (y)\)
Ideally, \(R = -\log p_x\) (MAP estimate)
\min_x \frac{1}{2}\|y - Ax \|_2^2 + R(x)
How to learn? ☹ \(p_x\) is unknown
LPN: Proximal Matching Training
\(\mathrm{prox}_{-\log p_x} (y)\)
Ideally, \(R = -\log p_x\) (MAP estimate)
\min_x \frac{1}{2}\|y - Ax \|_2^2 + R(x)
\(=\arg\max p(x \mid y)\)
\(= \arg\min_z \frac{1}{2}\|y - z \|_2^2 -\log p_x (z)\)
\(x \sim p_x, v \sim \mathcal{N}(0, \mathbf{I}), y = x + \sigma v\)
Prox is a MAP denoiser
Learn a MAP denoiser for data
LPN: Proximal Matching Training
\(x \sim p_x, v \sim \mathcal{N}(0, \mathbf{I}), y = x + \sigma v\)
\(\ell2\) \(\to\) E[x|y], MMSE
\(\ell1 \to\) Median[x|y]
argmax[x|y] ?
\(\min_{f} \mathbb{E}_{x,y} \mathcal{L}(f(y), x) \)
Train a denoiser \(f\):
LPN: Proximal Matching Training
\(x \sim p_x, v \sim \mathcal{N}(0, \mathbf{I}), y = x + \sigma v\)
\(\ell2\) \(\to\) E[x|y], MMSE
\(\ell1 \to\) Median[x|y]
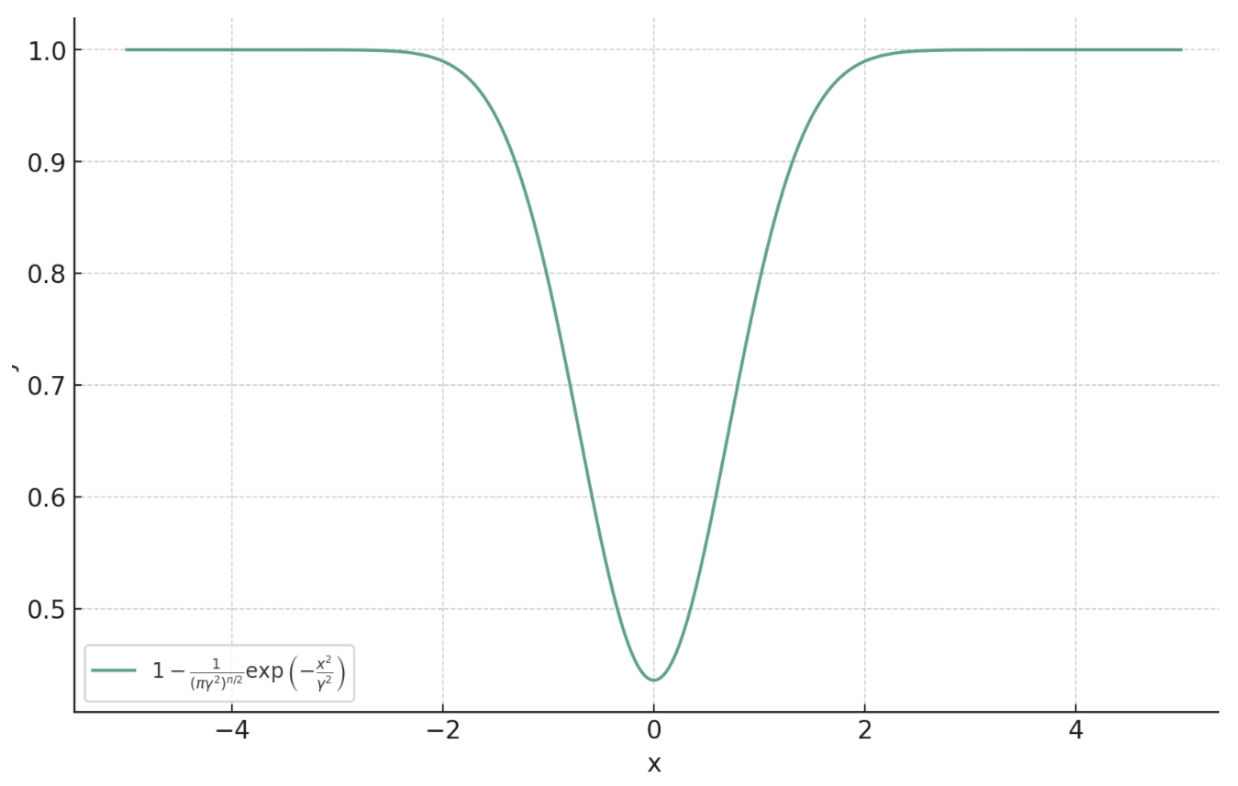
Theorem (informal). Let
\[f^* = \argmin_{f} \lim_{\gamma \searrow 0} \mathbb{E}_{x,y} \left[ m_\gamma \left( \|f(y) - x\|_2 \right) \right].\]
Then, almost surely (for almost all \(y\)),
\[f^*(y) = \argmax_{c} p_{x \mid y}(c) = \mathrm{prox}_{-\sigma^2\log p_x}(y).\]
\(m_{\gamma}(x) = 1 - \frac{1}{(\pi\gamma^2)^{n/2}}\exp\left(-\frac{x^2}{\gamma^2}\right)\)
Prox Matching Loss
Train a denoiser \(f\):
\(\min_{f} \mathbb{E}_{x,y} \mathcal{L}(f(y), x) \)
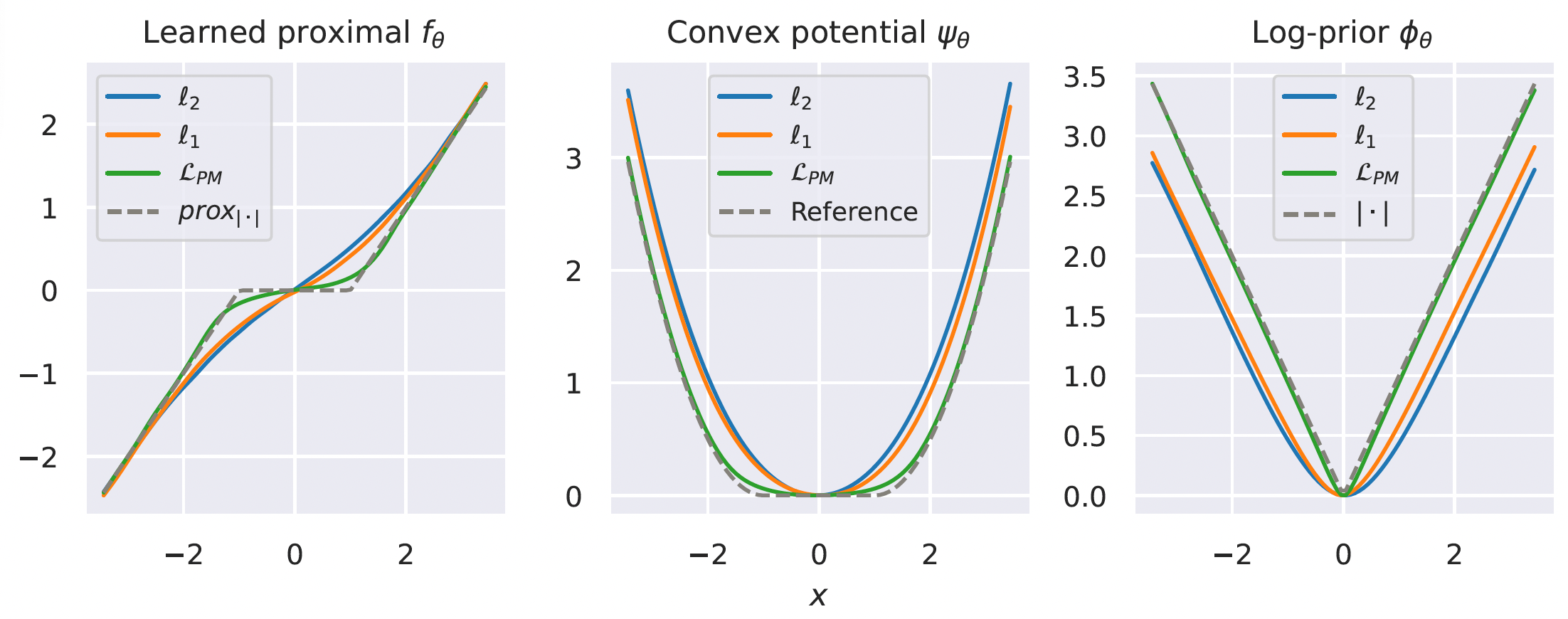
Learning a Prox for the Laplacian
Proximal matching is essential for learning the correct prox/prior
Learning a Prior for Hand-Written Digits
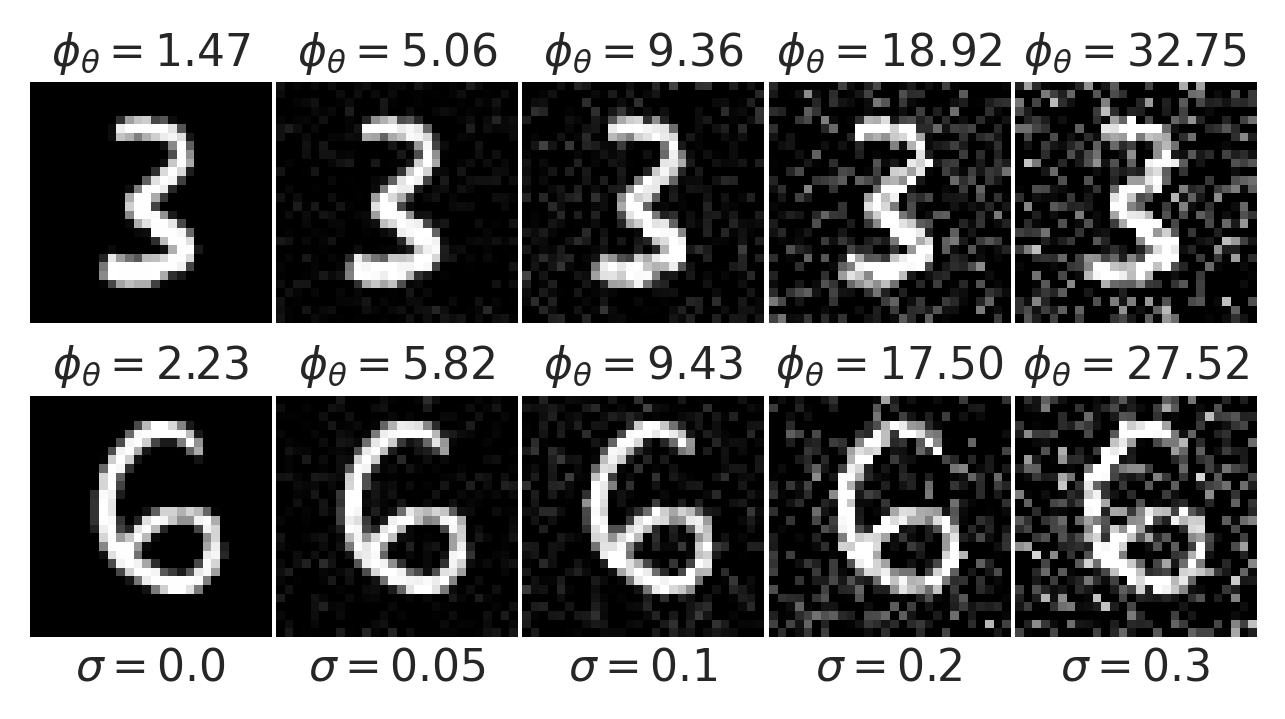
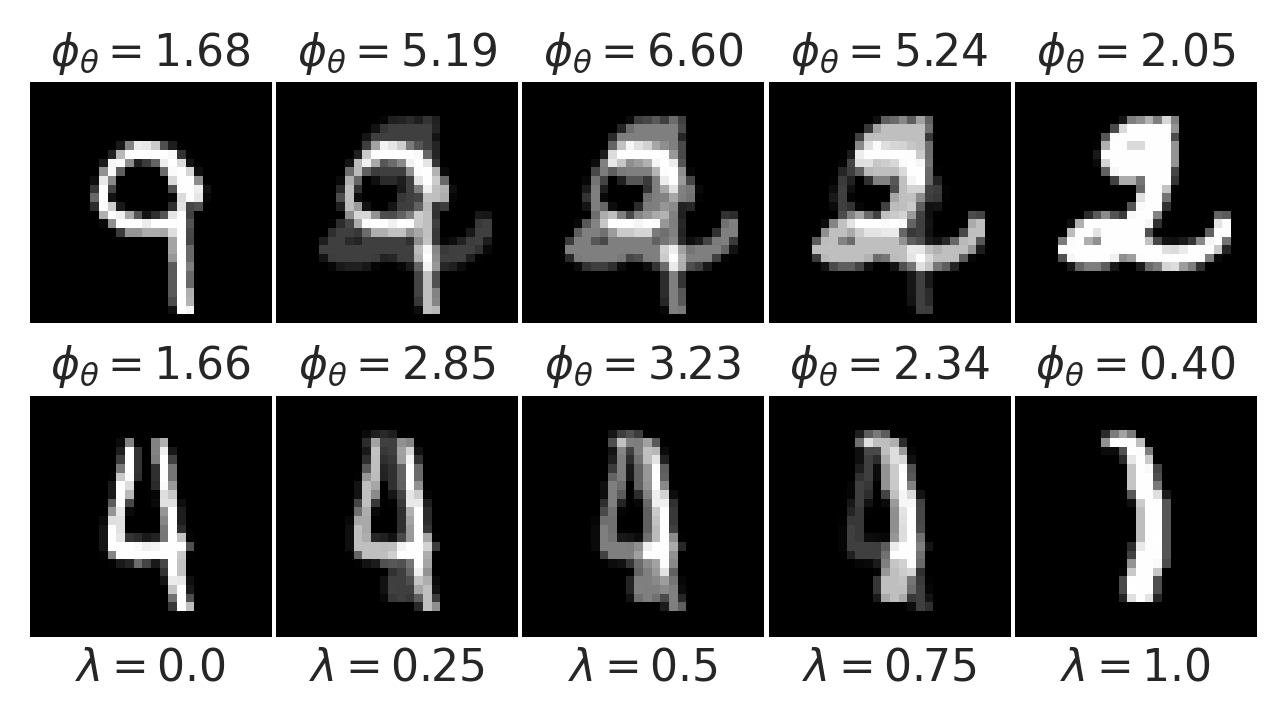
Gaussian noise
Convex interpolation
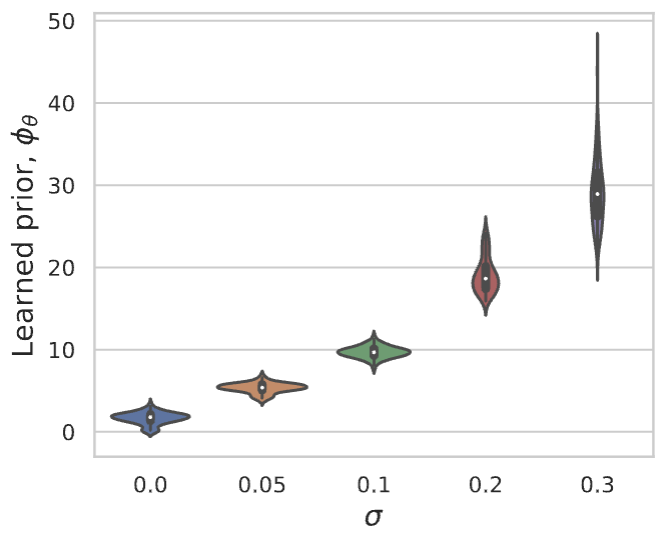
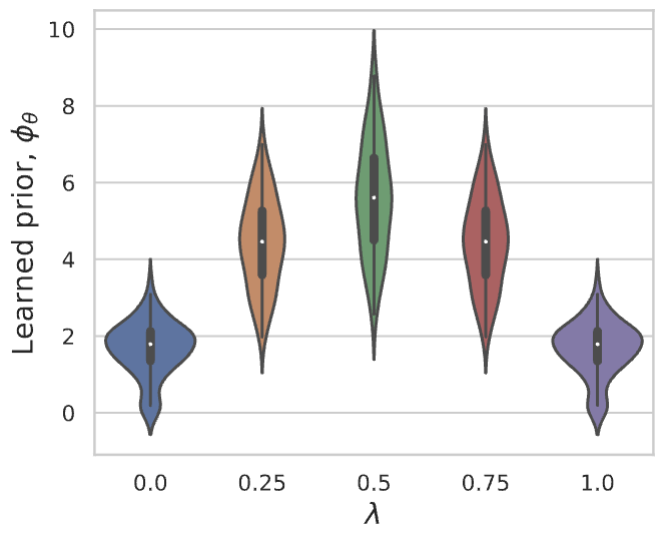
LPN faithfully captures distribution of natural images
Convergence Guarantee with LPN
Then, the iterates \(x_k\) converge to a fixed point, \(x^*\), that satisfies \(f_{\theta}\left(x^* - \eta \nabla h(x^*)\right) = x^*.\) Furthermore, \(x^*\) is also a critical point of \(h+ \tfrac{1}{\eta} R_\theta\).
Theorem (informal). Let \(h(x) = \tfrac{1}{2}\|y - Ax\|_2^2\). Consider the iterates resulting from running LPN with Plug-and-Play and proximal gradient descent:
$$x_{k+1} = f_{\theta}(x_k - \eta \nabla h(x_k)),$$with \(0 < \eta < 1/\| A^T A \|\).
Solving Inverse Problems with LPN
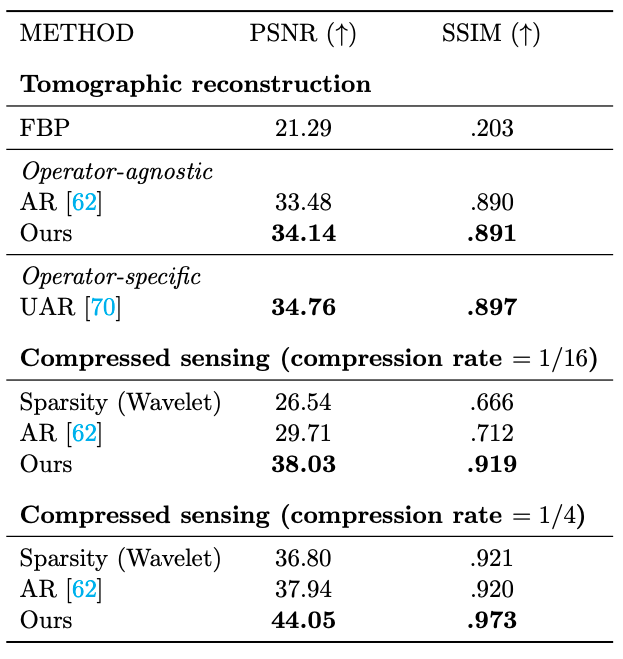
Sparse View Tomographic Reconstruction
Compressed Sensing
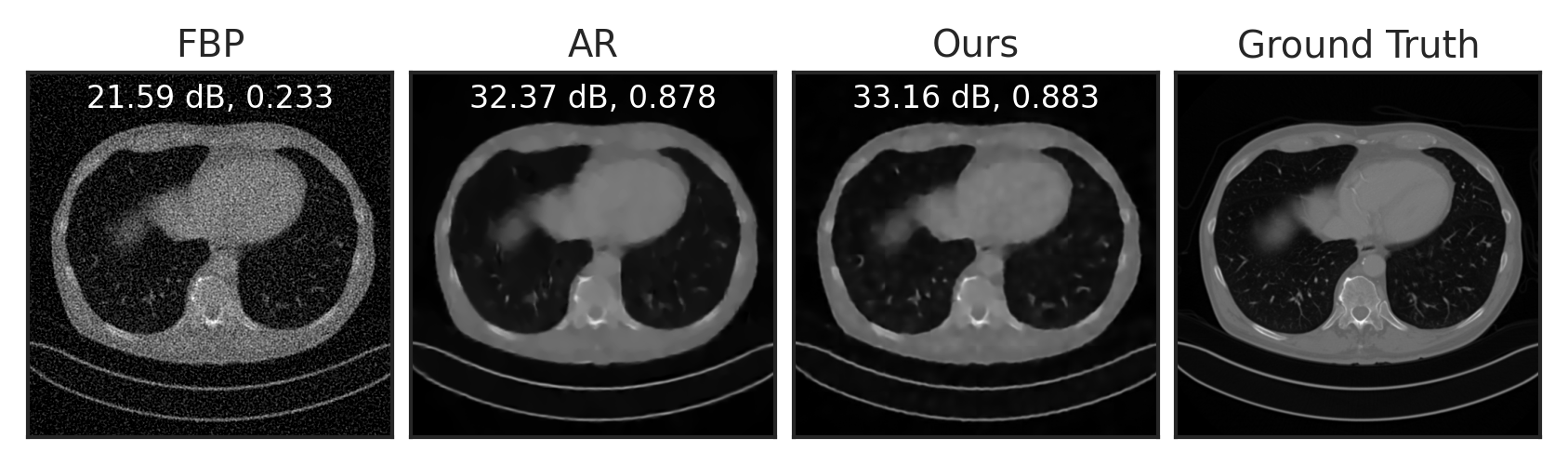
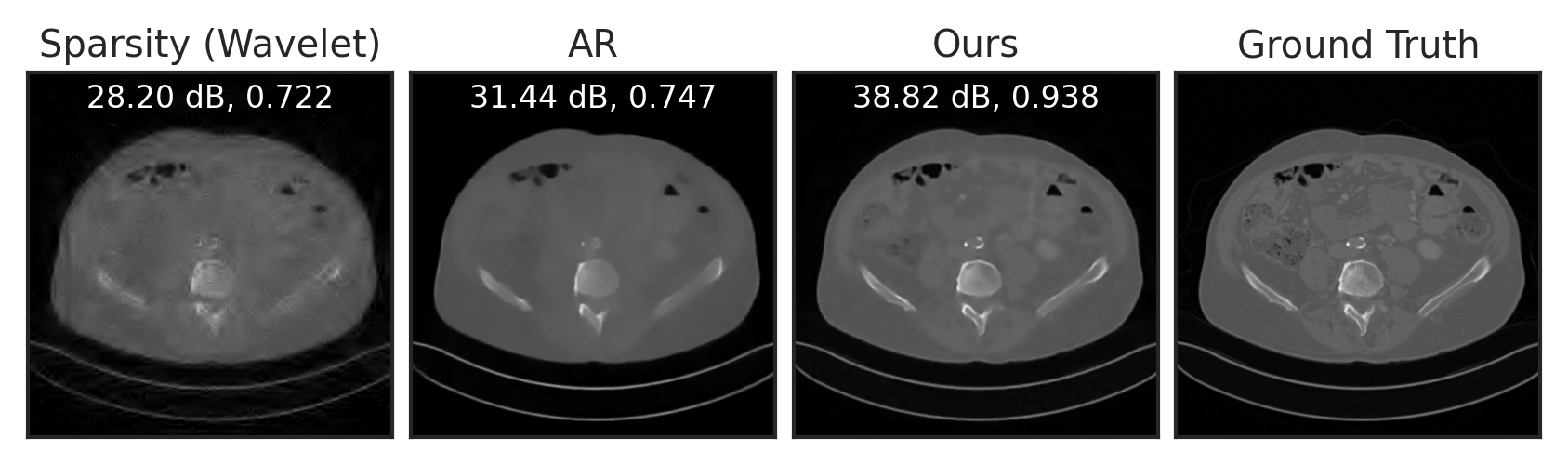
Solving Inverse Problems with LPN
Sparse View Tomographic Reconstruction
Compressed Sensing
Summary
- A new class of neural networks, learned proximal networks, that guarantee to parameterize proximal operators
- Characterization of implicit priors
- A new training paradigm, proximal matching, for learning the proximal of log prior from i.i.d. samples
- Convergence guarantees
- Competitive performance for inverse problems
Acknowledgements
- NIH NIBIB (P41EB031771)
- Distinguished Graduate Student Fellows program of the KAVLI Neuroscience Discovery Institute
CIS Retreat 20231208
By Zhenghan Fang
