Zhenghan Fang*, Sam Buchanan*, Jeremias Sulam
IMSI Computational Imaging Workshop
Wed, 7 Aug, 2024
*Equal contribution.
What's in a Prior?
Learned Proximal Networks for Inverse Problems
Inverse Problems
x
y
- Computational imaging
Measure
Inversion
y=Ax+v
Inverse Problems
MAP estimate
\min_x \tfrac{1}{2}\|y - Ax \|_2^2 + {\color{darkorange} R}(x)
{\color{darkorange} R} = -\log p_x
Prox. Grad. Desc.
x_{k+1} = {\color{darkorange}\mathrm{prox}_{\eta R}}(x_k - \eta A^H(A x_k - y))
Deep neural networks
{\color{darkorange}\mathrm{prox}_{R}} (z) = \argmin_u \tfrac{1}{2} \|u-z\|_2^2 + R(u)
Proximal Operator
x_{k+1} = \quad {\color{red}f_{\theta}} \quad \ (x_k - \eta A^H(A x_k - y))
Plug-n-Play
Questions and Contributions
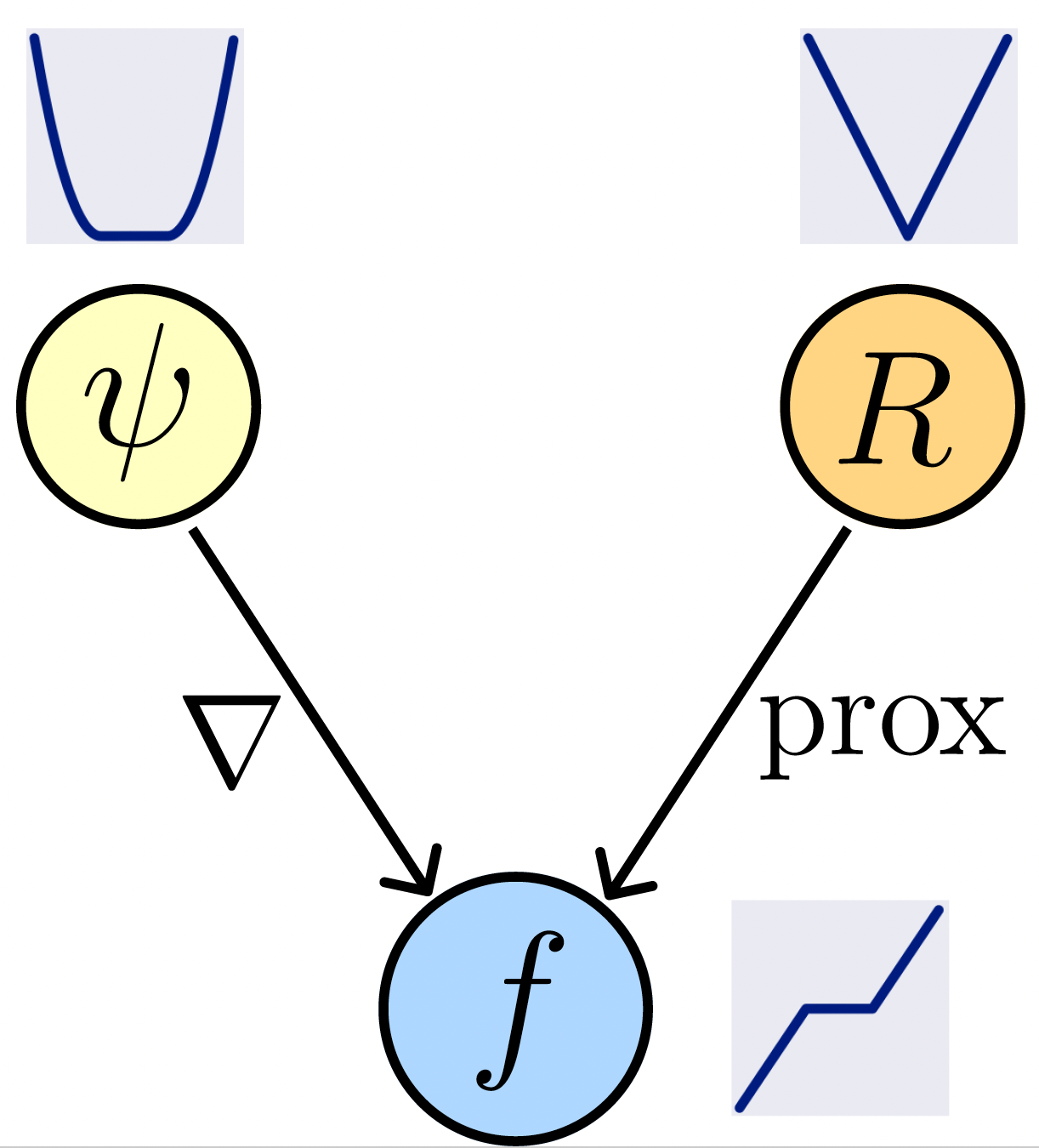
1. When is a neural network \(f_\theta\) a proximal operator?
2. What's the prior \(R\) learned by the neural network \(f_\theta\)?
3. How can we learn the prox of the true prior?
4. Convergence guarantees for PnP
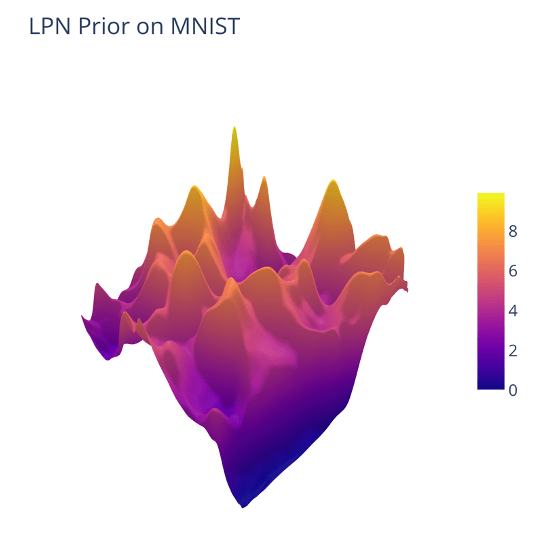
Prior Landscape
Proximal Matching Loss
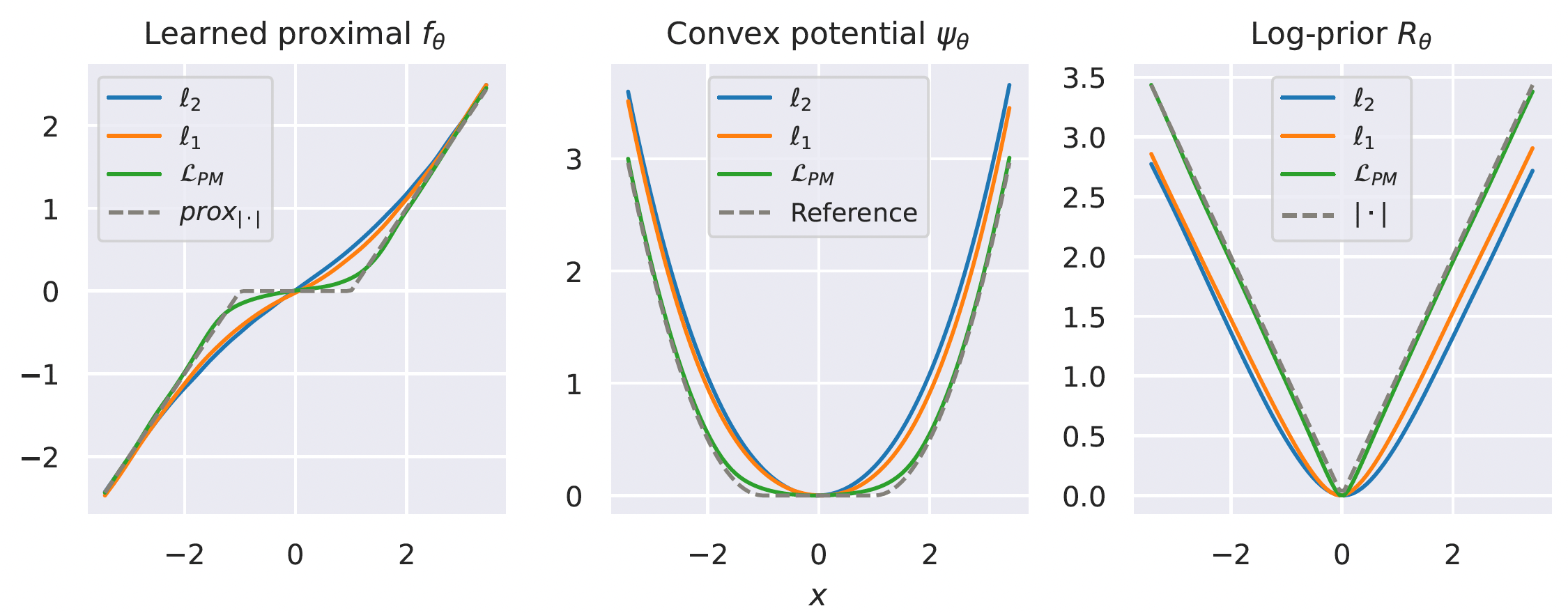
Learned proximal networks (LPN)
neural networks for prox. operators
Questions and Contributions
1. When is a neural network \(f_\theta\) a proximal operator?
2. What's the prior \(R\) learned by the neural network \(f_\theta\)?
3. How can we learn the prox of the true prior?
4. Convergence guarantees for PnP
Prior Landscape
Proximal Matching Loss
Learned proximal networks (LPN)
neural networks for prox. operators
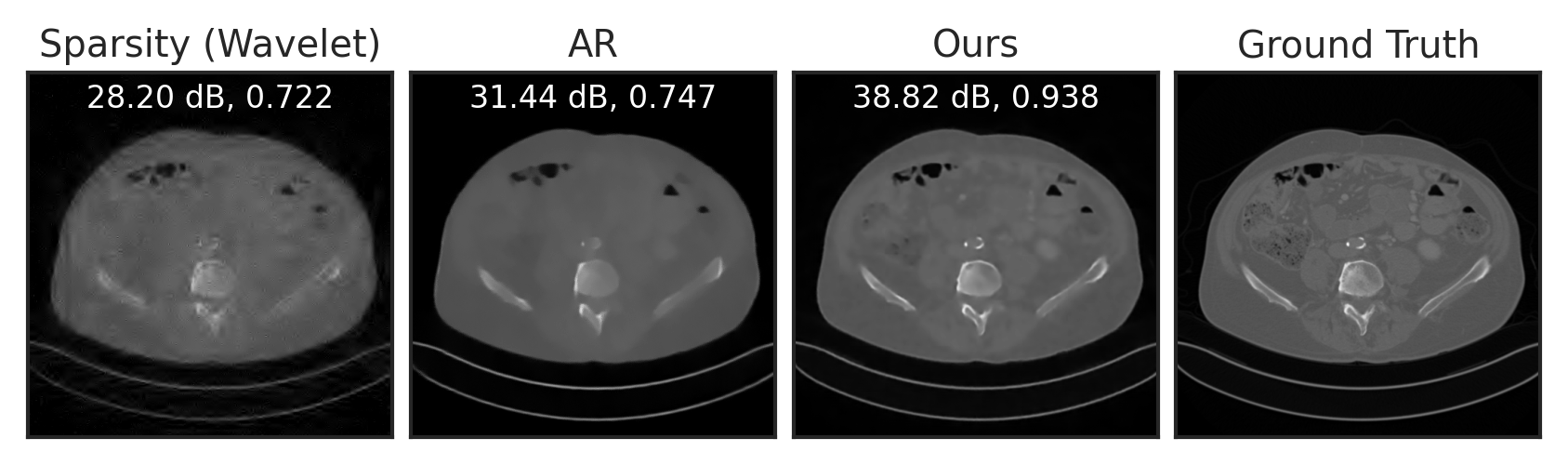
Compressed Sensing
Acknowledgements and References
Fang, Buchanan, Sulam. What's in a Prior? Learned Proximal Networks for Inverse Problems. ICLR 2024.
Sam Buchanan
TTIC
Jeremias Sulam
JHU
Inverse Problems
y=Ax+v
\min_x \tfrac{1}{2}\|y - Ax \|_2^2 + {\color{darkorange} R}(x)
MAP estimate
x_{k+1} = {\color{darkorange}\mathrm{prox}_{\eta R}}(x_k - \eta A^H(A x_k - y))
x_{k+1} = \argmin_x\tfrac{1}{2} \| y - Ax \|_2^2 + \tfrac{\rho}{2} \|z_k - u_k - x\|_2^2
u_{k+1} = u_k + x_{k+1} - z_k
z_{k+1} = {\color{darkorange} \mathrm{prox}_{R/\rho}}(u_{k+1} + x_{k+1})
Proximal Gradient Descent
ADMM
{\color{darkorange} R} = -\log p_x
\[{\color{darkorange}\mathrm{prox}_{R}} (z) = \argmin_u \tfrac{1}{2} \|u-z\|_2^2 + R(u)\]
MAP denoiser
Prox Operator
Plug-and-Play: replace \({\color{darkorange} \mathrm{prox}_{R}}\) by off-the-shelf denoisers
Inverse Problems
y=Ax+v
MAP estimate
- When is a neural network \(f_\theta\) a proximal operator?
- What's the prior \(R\) in the neural network \(f_\theta\)?
Questions
x_{k+1} = {\color{red}f_{\theta}}(x_k - \eta A^H(A x_k - y))
x_{k+1} = \argmin_x\tfrac{1}{2} \| y - Ax \|_2^2 + \tfrac{\rho}{2} \|z_k - u_k - x\|_2^2
u_{k+1} = u_k + x_{k+1} - z_k
z_{k+1} = {\color{red} f_\theta }(u_{k+1} + x_{k+1})
PnP-PGD
PnP-ADMM
SOTA Neural Network based Denoisers...
\min_x \tfrac{1}{2}\|y - Ax \|_2^2 + {\color{darkorange} R}(x)
{\color{darkorange} R} = -\log p_x
Proximal Matching
\(\ell_2\) loss \(\implies\) E[x|y], MMSE denoiser
\(\ell_1\) loss \(\implies\) Median[x|y]
Can we learn the proximal operator of an unknown prior?
\(f_\theta = \mathrm{prox}_{-\log p_x}\)
\(R_\theta = -\log p_x\)
But we want...
\(\mathrm{prox}_{-\log p_x} = \) Mode[x|y], MAP denoiser
Conventional losses do not suffice!
Prox Matching Loss
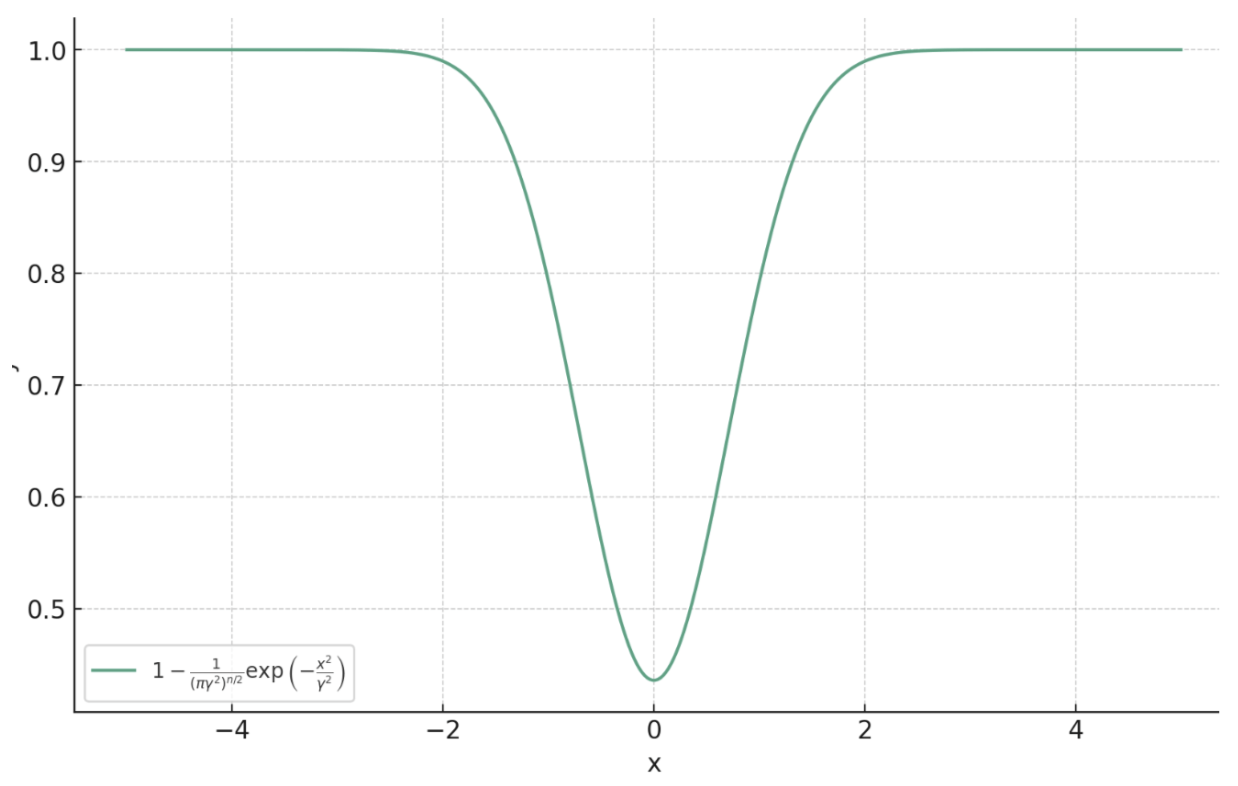
\[\ell_{\text{PM}, \gamma}(x, y) = 1 - \frac{1}{(\pi\gamma^2)^{n/2}}\exp\left(-\frac{\|f_\theta(y) - x\|_2^2}{ \gamma^2}\right)\]
\gamma
Learning the prox of a Laplacian distribution
Learned Proximal Networks
Proposition (Learned Proximal Networks, LPN).
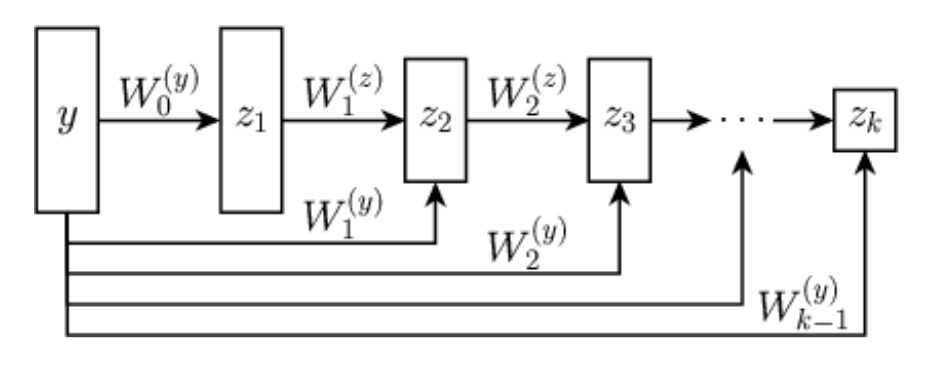
Let \(\psi_\theta: \R^{n} \rightarrow \R\) be defined by \[z_{1} = g( \mathbf H_1 y + b_1), \quad z_{k} = g(\mathbf W_k z_{k-1} + \mathbf H_k y + b_k), \quad \psi_\theta(y) = \mathbf w^T z_{K} + b\]
with \(g\) convex, non-decreasing, and all \(\mathbf W_k\) and \(\mathbf w\) non-negative.
Let \(f_\theta = \nabla \psi_{\theta}\). Then, there exists a function \(R_\theta\) such that \(f_\theta(y) = \mathrm{prox}_{R_\theta}(y)\).
Neural networks that guarantee to parameterize proximal operators
Proximal Matching
\(\ell_2\) loss \(\implies\) E[x|y], MMSE denoiser
\(\ell_1\) loss \(\implies\) Median[x|y]
Can we learn the proximal operator of an unknown prior?
\(f_\theta = \mathrm{prox}_{-\log p_x}\)
\(R_\theta = -\log p_x\)
Conventional losses do not suffice!
Prox Matching Loss
\[\ell_{\text{PM}, \gamma}(x, y) = 1 - \frac{1}{(\pi\gamma^2)^{n/2}}\exp\left(-\frac{\|f_\theta(y) - x\|_2^2}{ \gamma^2}\right)\]
\gamma
Theorem (Prox Matching, informal).
Let
\[f^* = \argmin_{f} \lim_{\gamma \searrow 0} \mathbb{E}_{x,y} \left[ \ell_{\text{PM}, \gamma} \left( x, y \right)\right].\]
Then, almost surely (for almost all \(y\)),
\[f^*(y) = \argmax_{c} p_{x \mid y}(c) = \mathrm{prox}_{-\alpha\log p_x}(y).\]
But we want...
\(\mathrm{prox}_{-\log p_x} = \) Mode[x|y], MAP denoiser
Learned Proximal Networks
LPN provides convergence guarantees for PnP algorithms under mild assumptions.
Theorem (Convergence of PnP-ADMM with LPN, informal)
Consider running LPN with Plug-and-Play and ADMM with a linear forward operator \(A\). Assume the ADMM penalty parameter satisfies \(\rho > \|A^TA\|\). Then, the sequence of iterates converges to a fixed point of the algorithm.
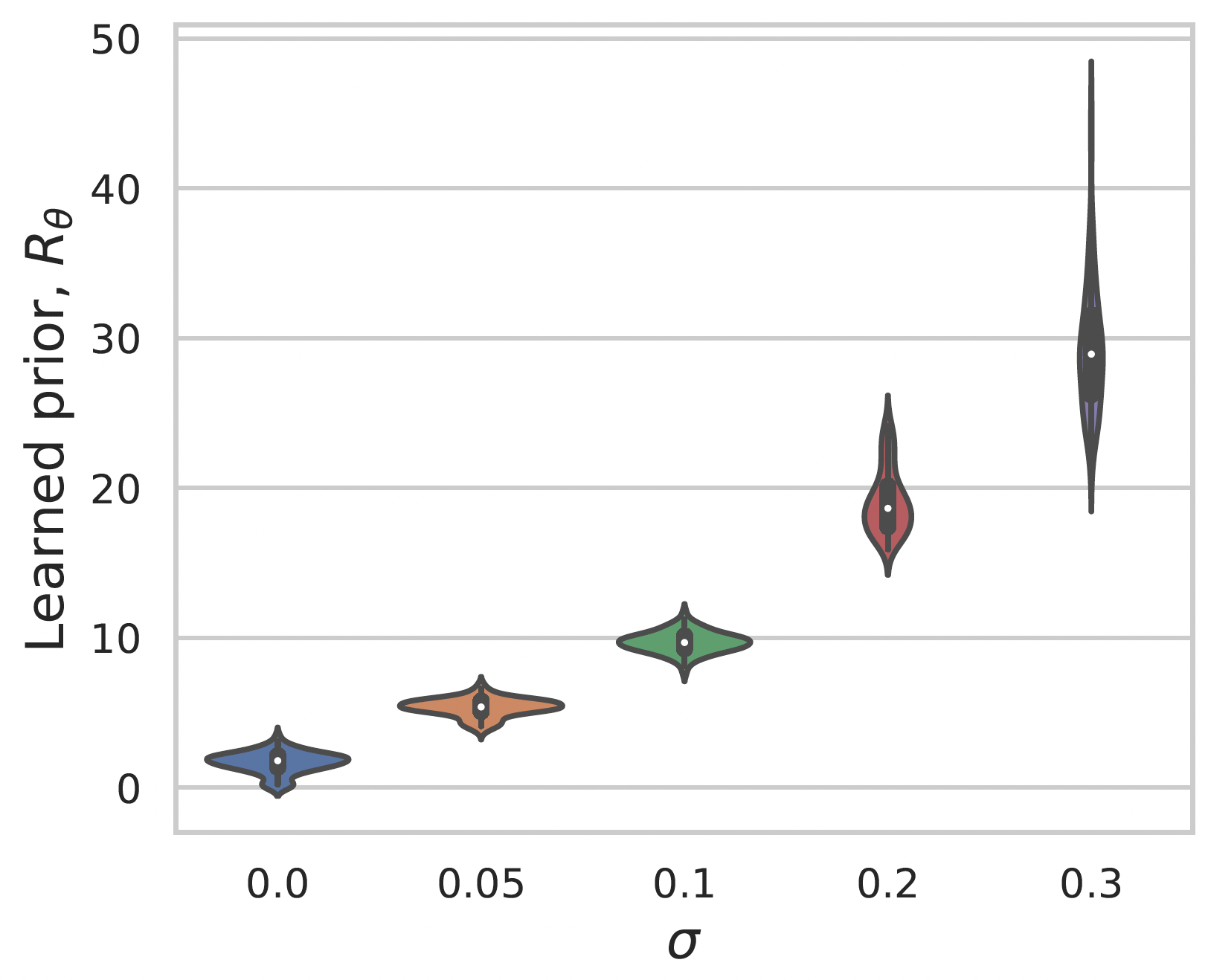
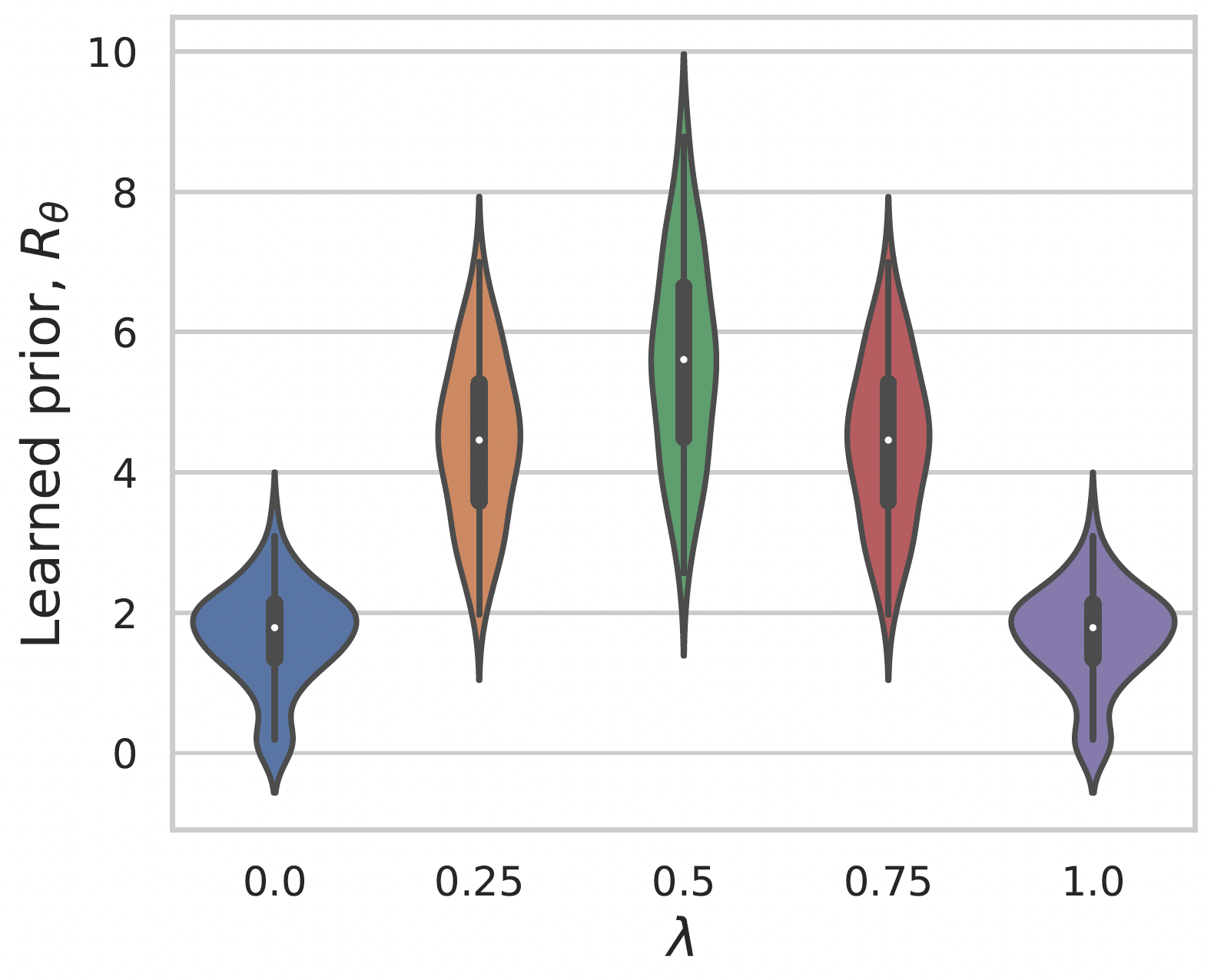
Learning a prior for MNIST images
Gaussian noise
Convex interpolation
Summary
- Learned proximal networks parameterize proximal operators, by construction
- Proximal matching: learn the proximal of an unknown prior
- Interpretable priors for inverse problem
- Convergent PnP with LPN
Fang, Buchanan, Sulam. What's in a Prior? Learned Proximal Networks for Inverse Problems. ICLR 2024.
Sam Buchanan
TTIC
Jeremias Sulam
JHU
IMSI Computational Imaging Workshop 2024 3min
By Zhenghan Fang
