Topology in physics
Zhi Han
Definition of topological space: 20th century
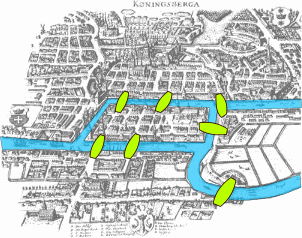
First problem: 17th century
Point set topology is a disease from which the human race will soon recover.
Henri Poincaré
- ZFC Set Theory (more fundamental)
- Topology
- Algebra
- Geometry
- Calculus
- Linear Algebra (first year math)
- ...
Is topology fundamental? Absolutely.
Is topology useful?
"for theoretical discoveries of topological phase transitions and topological phases of matter"
Nobel Prize in Physics 2016
- The quantum Hall effect
- Idea 1: Bulk-edge correspondence.
-
Aharonov–Bohm effect
- Idea 2: Topology and Algebra
- The Kitaev Chain (the focus of this talk)
- Idea 3: Topological phases
- Topological qubits
- Idea 4: Fault Tolerance
B
e^-
Grid of electrons
Quantum Hall effect
B
e^-
Quantum Hall effects: Current on the boundary of quantum matter; No current on the inside
Bulk-edge correspondence
When the physics is different on the bulk vs. the edge.
(What in the world is topological quantum matter? - Fan Zhang)
- This topological feature is called Bulk-edge correspondence.
- Insulator on the interior, conductor on the boundary.
- Topological Insulator.
e^-
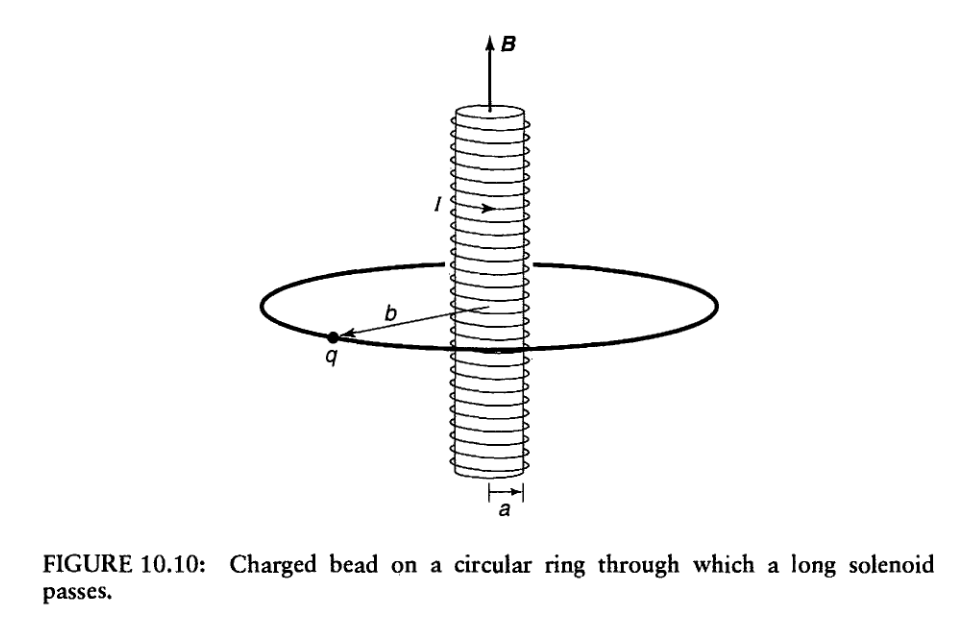
(Griffths Introduction to QM)
Aharonov–Bohm effect
\exp(ie\Phi)
\(\Phi\): Magnetic flux
\exp(ie\Phi)
The accumulated phase does not depend on the path taken. Geometric phase:
{\displaystyle \gamma _{n}[C]=i\oint _{C}\langle n,t|{\big (}\nabla _{R}|n,t\rangle {\big )}\,dR}
(Griffths Introduction to QM)
Why?
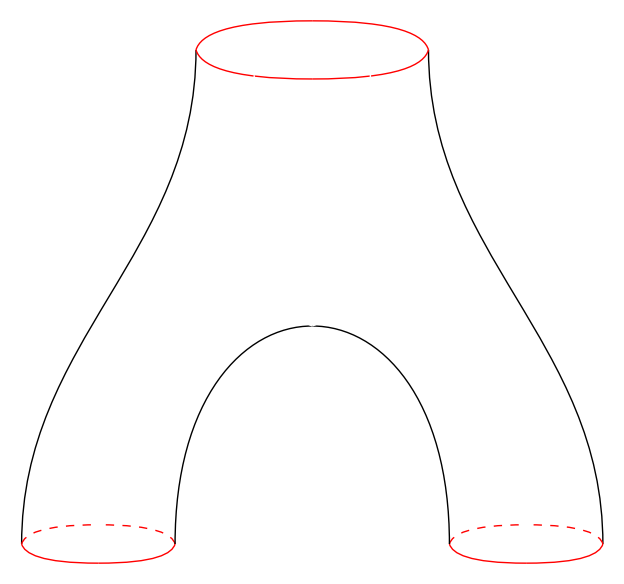
Winding numbers of a loop can be defined as the number of times the loop goes around a "hole" counterclockwise.
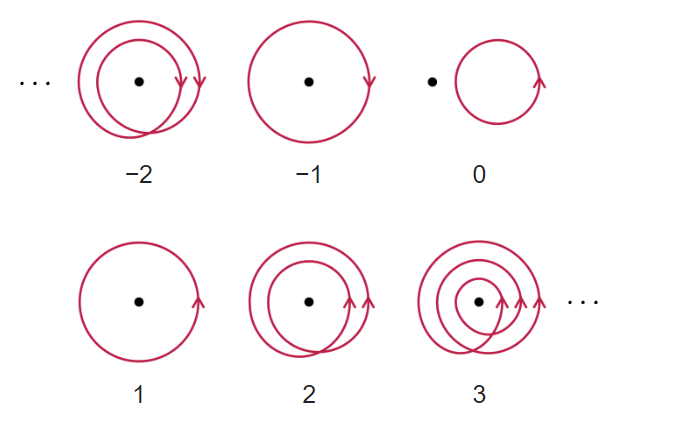
Integers: \(\mathbb{Z}\)
A curve has winding number zero if we can contract it to a point.
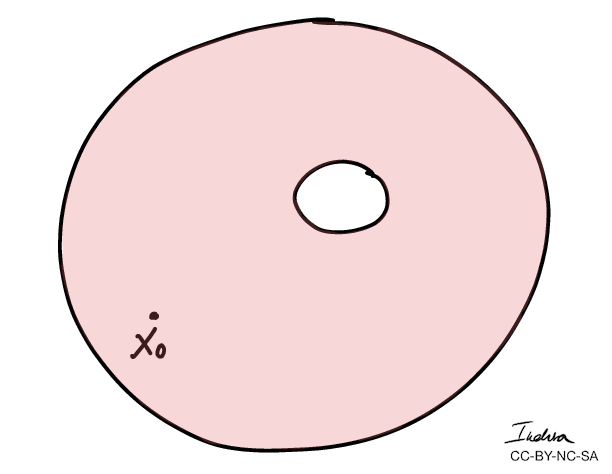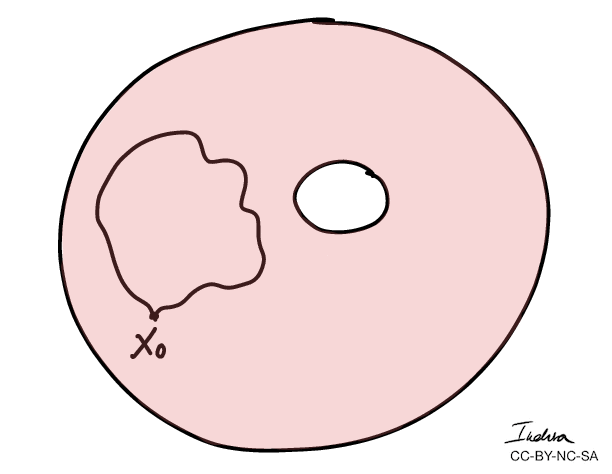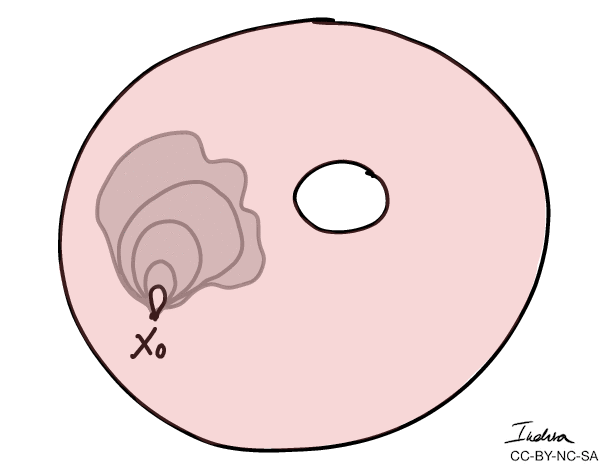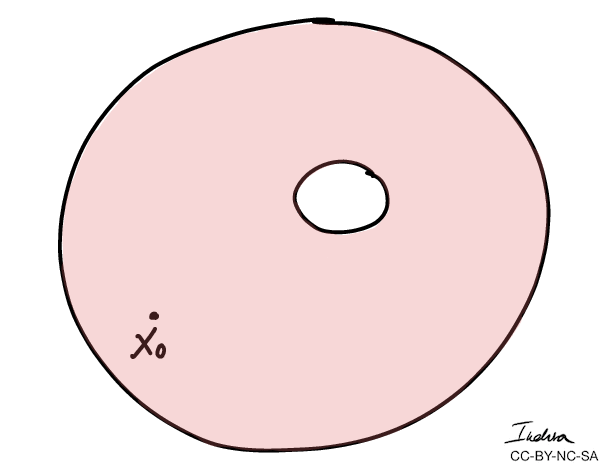
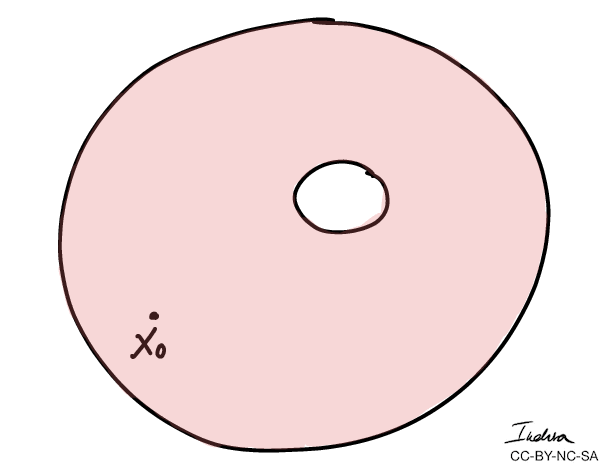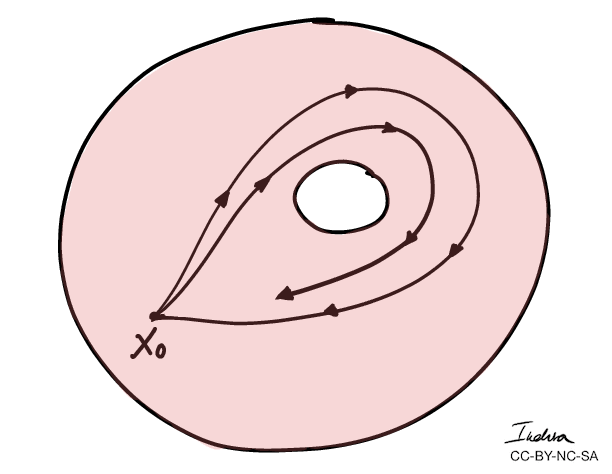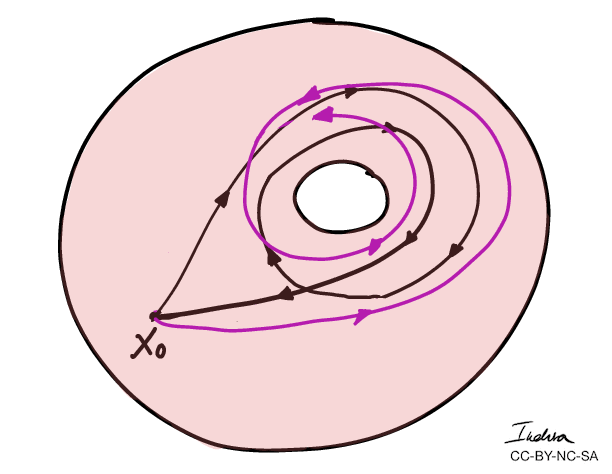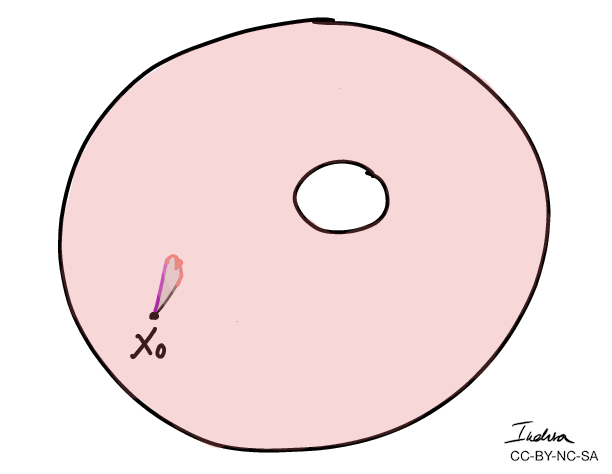
- More importantly, we can use winding numbers to classify topological spaces.
- The winding numbers of the combined curves \(C_1 + C_2 \) is 0.
2 + (-2) = 0
- The winding numbers forms an algebraic group: \((\mathbb{Z}, +)\)
- We've just assigned an algebraic object: \(\mathbb{Z}\) to a topological invariant: a hole.
- In algebraic topology: fundamental group.
=\mathbb{Z}
= \mathbb{Z}
= \mathbb{Z}
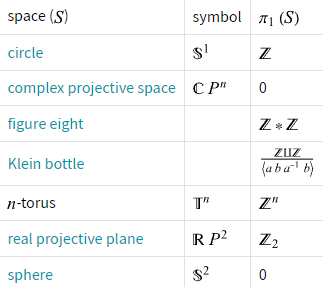
Fundamental group
-
Topology looks at invariant properties of objects under continuous transformations.
-
The converse is true: objects that share the same topological invariants are the same topologically.
= \mathbb{Z}
= \mathbb{Z}
\therefore
=
\blacksquare
(Wikipedia)
= \mathbb{Z}
= \mathbb{Z} \times \mathbb{Z} \times \mathbb{Z}
\neq
\exp(ie\Phi)
\exp(ie\Phi)
{\displaystyle \mathbf {B} =\mathbf {0} =\nabla \times \mathbf {A} }
Outside solenoid:
\displaystyle \mathbf{A} = \frac{\Phi}{2\pi r}\hat \phi
Plot of \(\mathbf{A}\): magnetic vector potential in a solenoid
\gamma ={\displaystyle \oint _{C}\frac{1}{z}dz} = {\displaystyle \int_0^{2\pi}\frac{1}{e^{i\theta}}ie^{i\theta}d\theta}=2\pi i
Topological reason: \(\mathbf{A}\) has a hole.
de Rham cohomology, which (roughly speaking) measures precisely the extent to which the fundamental theorem of calculus fails in higher dimensions and on general manifolds. (Terence Tao)
this failure is related to the possible existence of "holes" in the manifold. (Wikipedia)
{\displaystyle \oint _{\gamma }f(z)\,dz=2\pi i\sum _{k=1}^{n}\operatorname {I} (\gamma ,a_{k})\operatorname {Res} (f,a_{k}).}
Residue theorem.
"\(f\) is \(2\pi i \times \) winding number \(\times\) number of holes \(\times\) residue."
\hat{c}^{\dagger}=\frac{1}{2}\left(\hat{\gamma}_{1}+i \hat{\gamma}_{2}\right)
- Majorana fermion: particle that is its own antiparticle.
- Valid solution to the Dirac equation.
- 1 electron = 2 Majoranas.
- Obeys anticommutation algebra of fermions.
\mathcal{H}=\sum_{n m} H_{n m} c_{n}^{\dagger} c_{m}+\frac{1}{2}\left(\Delta_{n m} c_{n}^{\dagger} c_{m}^{\dagger}+\Delta_{n m}^{*} c_{m} c_{n}\right)
Topological Invariant
- The topological invariant is the sign (+/-) of the ground state.
Superconductors
\mathcal{H}=\sum_{n m} H_{n m} c_{n}^{\dagger} c_{m}+\frac{1}{2}\left(\Delta_{n m} c_{n}^{\dagger} c_{m}^{\dagger}+\Delta_{n m}^{*} c_{m} c_{n}\right)
\mathcal{H}=\frac{1}{2} C^{\dagger} \left(\begin{array}{cc}
H & \Delta \\
-\Delta^{*} & -H^{*}
\end{array}\right) C
C = [ c_1 \ldots c_n, c^\dagger_1 \ldots c^\dagger_n]
Rewrite as quadratic form
Vector of creation and annhilation operators
Bogoliubov-de Gennes
Hamiltonian. \(H_{BdG}\)
Topological properties?
C = [ c_1 \ldots c_n, c^\dagger_1 \ldots c^\dagger_n]
\mathcal{H}=\frac{1}{2} C^{\dagger} \left(\begin{array}{cc}
H & \Delta \\
-\Delta^{*} & -H^{*}
\end{array}\right) C
Particle hole symmetry
How to generate Majoranas
The Kitaev chain is just \(n\) electrons in a row:
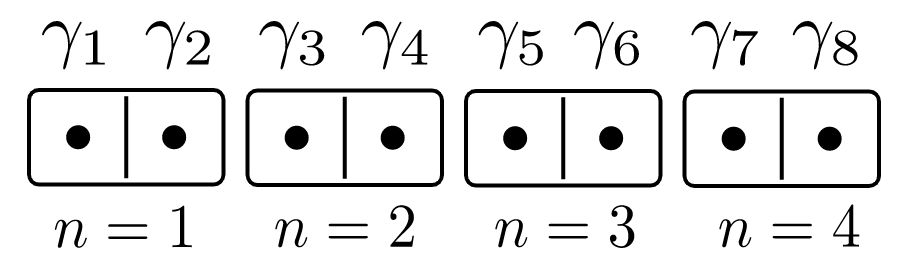
Let's saw an electron in half!
The Trivial Phase
H=(i / 2) \mu \sum_{n=1}^{N} \gamma_{2 n-1} \gamma_{2 n} \quad \text {(trivial phase)}
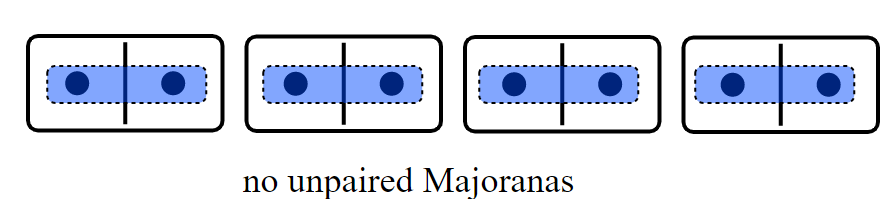
No unpaired Majoranas, and each Majorana pair has energy \(\mu/2\) (ansatz):
The Topological Phase
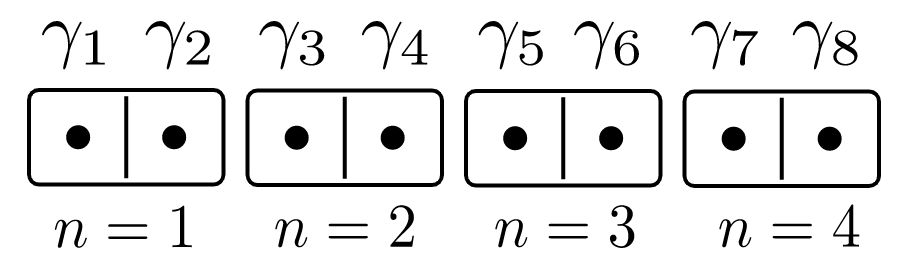
Or like this, each Majorana pair has an energy \(t\):
H=i t \sum_{n=1}^{N-1} \gamma_{2 n} \gamma_{2 n+1} \quad \text{(topological phase)}
H=(i / 2) \mu \sum_{n=1}^{N} \gamma_{2 n-1} \gamma_{2 n} \quad \text {(trivial phase)}
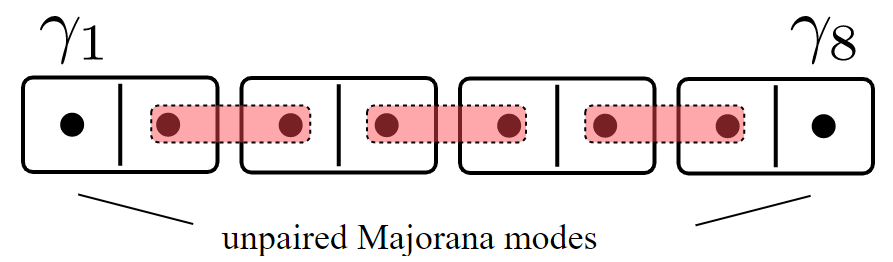
The Kitaev Chain
H=i t \sum_{n=1}^{N-1} \gamma_{2 n} \gamma_{2 n+1} \quad \text{(topological phase)}
H=(i / 2) \mu \sum_{n=1}^{N} \gamma_{2 n-1} \gamma_{2 n} \quad \text {(trivial phase)}
Rewrite as fermions:
The Kitaev Chain
\begin{aligned}
H=&-\mu \sum_{n} c_{n}^{\dagger} c_{n}\\
&-t \sum_{n}\left(c_{n+1}^{\dagger} c_{n}+\mathrm{h.c.}\right)\\
&+\Delta \sum_{n}\left(c_{n} c_{n+1}+\mathrm{h.c.}\right)
\end{aligned}
H=i t \sum_{n=1}^{N-1} \gamma_{2 n} \gamma_{2 n+1} \quad \text{(topological phase)}
H=(i / 2) \mu \sum_{n=1}^{N} \gamma_{2 n-1} \gamma_{2 n} \quad \text {(trivial phase)}
Rewrite as fermions: Obtain Hamiltonian of a superconductor.
\(\mu\) = chemical potential
\(t\) = kinetic energy
\(\Delta\) = superconducting band gap/Cooper pairs
H=-\mu \sum_{n} c_{n}^{\dagger} c_{n}-t \sum_{n}\left(c_{n+1}^{\dagger} c_{n}+\mathrm{h.c.}\right)\\+\Delta \sum_{n}\left(c_{n} c_{n+1}+\mathrm{h.c.}\right)
H=i t \sum_{n=1}^{N-1} \gamma_{2 n} \gamma_{2 n+1} \\\text{(topological phase)}
H=(i / 2) \mu \sum_{n=1}^{N} \gamma_{2 n-1} \gamma_{2 n} \\ \text {(trivial phase)}
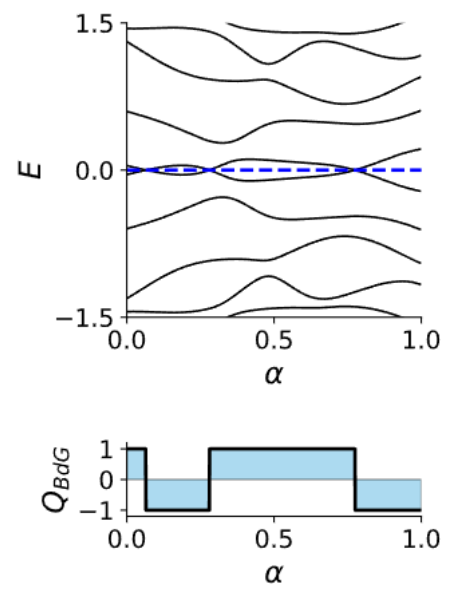
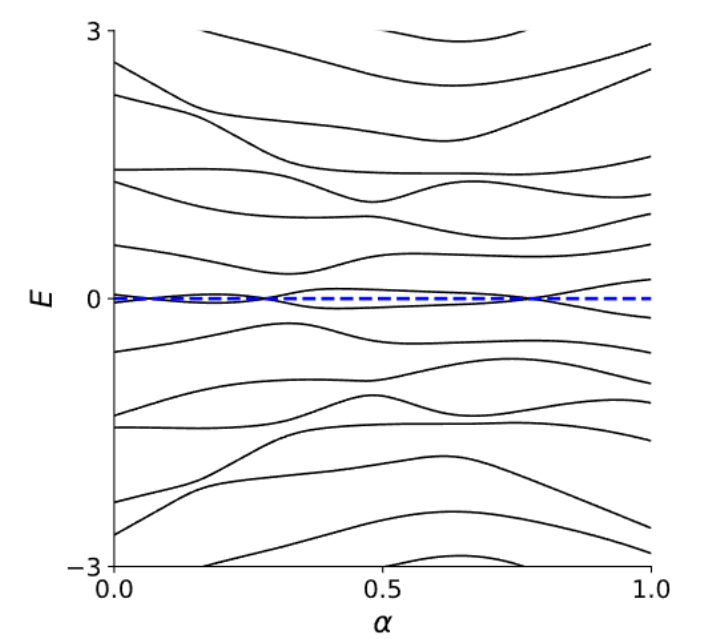
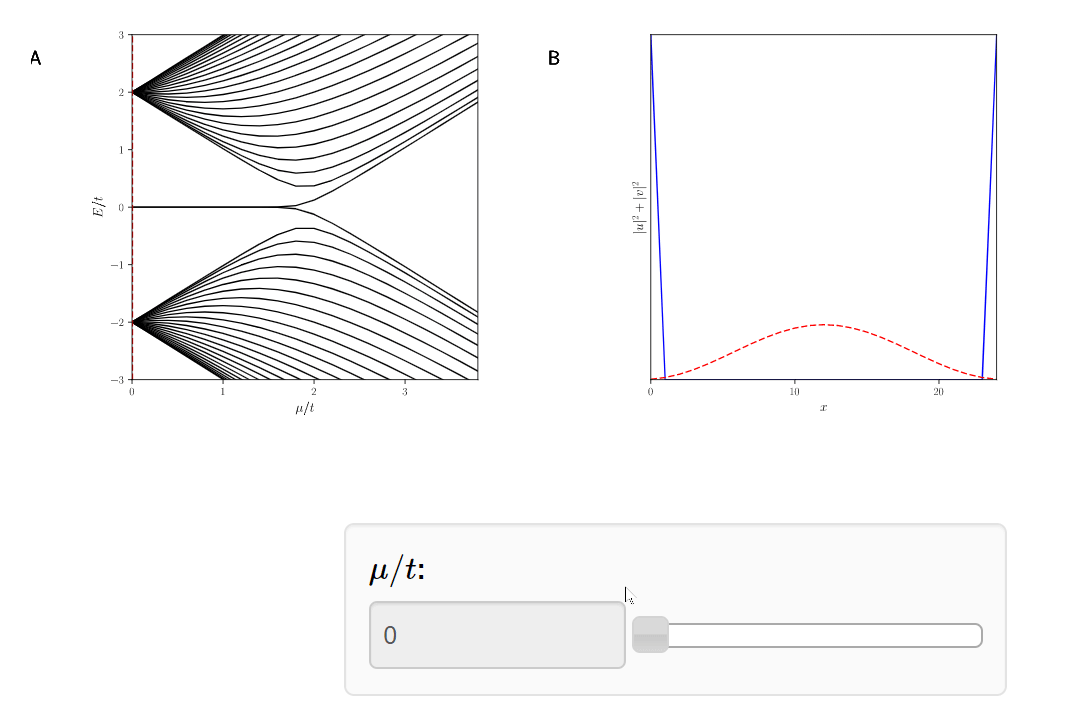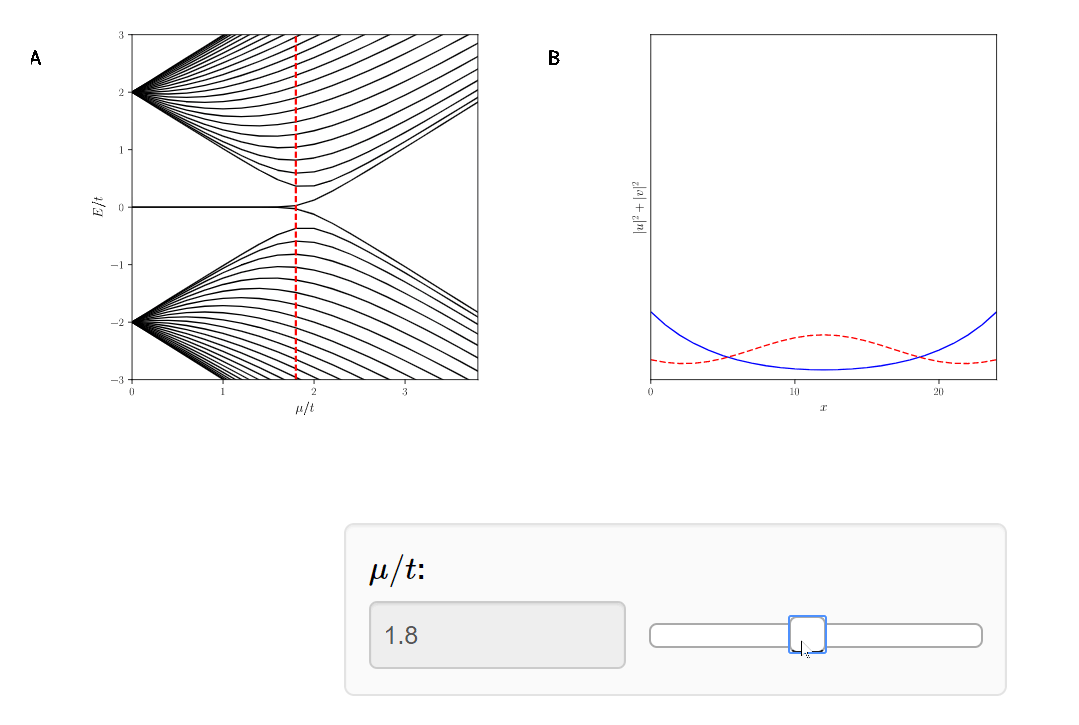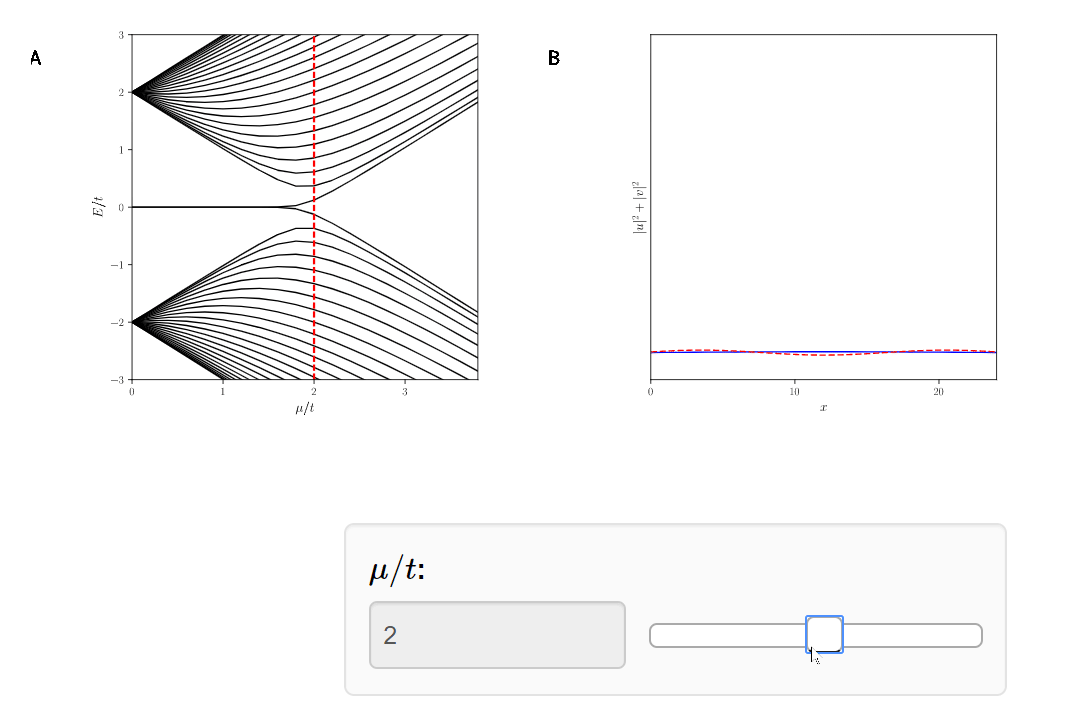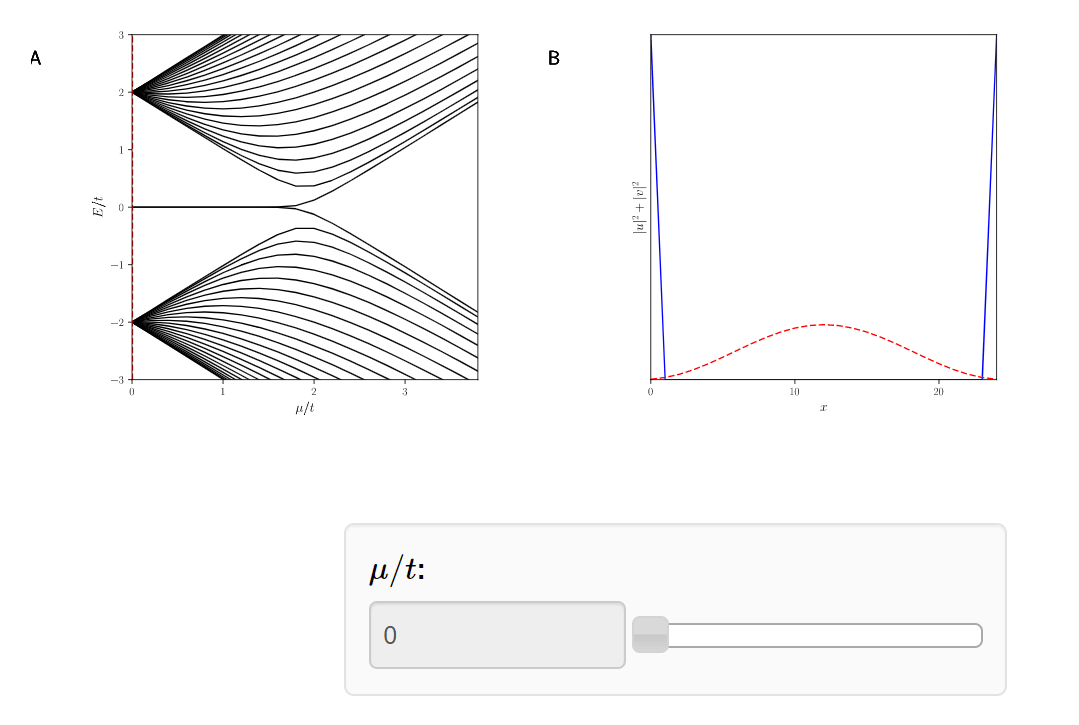
Topological
phase transition at \(\mu = 2t\)
Topological \( |\mu|<2t\)
Trivial \( |\mu|\geq2t\)
Topological
phase transition at \(\mu = 2t\)
Topological \( |\mu|<2t\)
Trivial \( |\mu|\geq2t\)
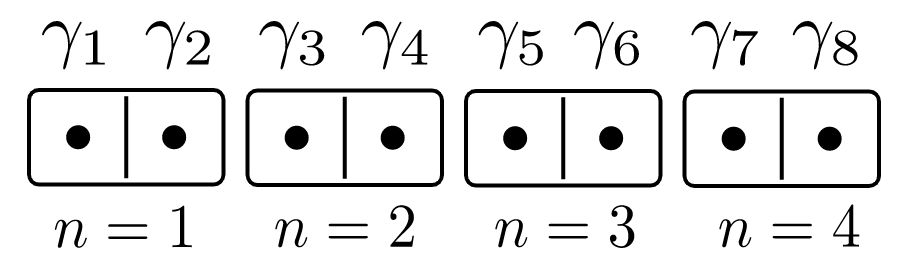
Why do we care?
The Majoranas are a topological property of the system. If one electron falls off the chain, a new Majorana will appear.
- Bulk-edge correspondence!
- Highly desirable for quantum computing.
- The topological invariant corresponds to the topological phase.
- Q = -1 (topological)
- Q = +1 (trivial)
- Two topological phases: \(\mathbb{Z}_2 = \{1, -1\}\) (or \(\{0, +1\}\))
Topological Phase Transition
\psi
x
E/t
\mu/t
Classification of Topological Superconductors
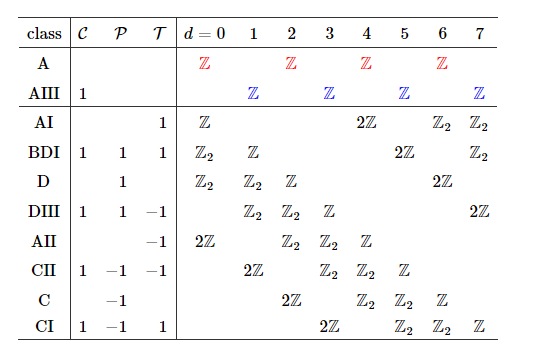
- \(d\) = dimension
- \(\mathcal{C}\) = charge symmetry
- \(\mathcal{P}\) = parity symmetry
- \(\mathcal{T}\) = time symmetry
- Quantum Hall effect: \(\mathbb{Z}\)
- Kitaev chain: \(\mathbb{Z_2}\)
- Classified by topological phases.
Store quantum information in the Majorana?
Main idea behind topological quantum computing.
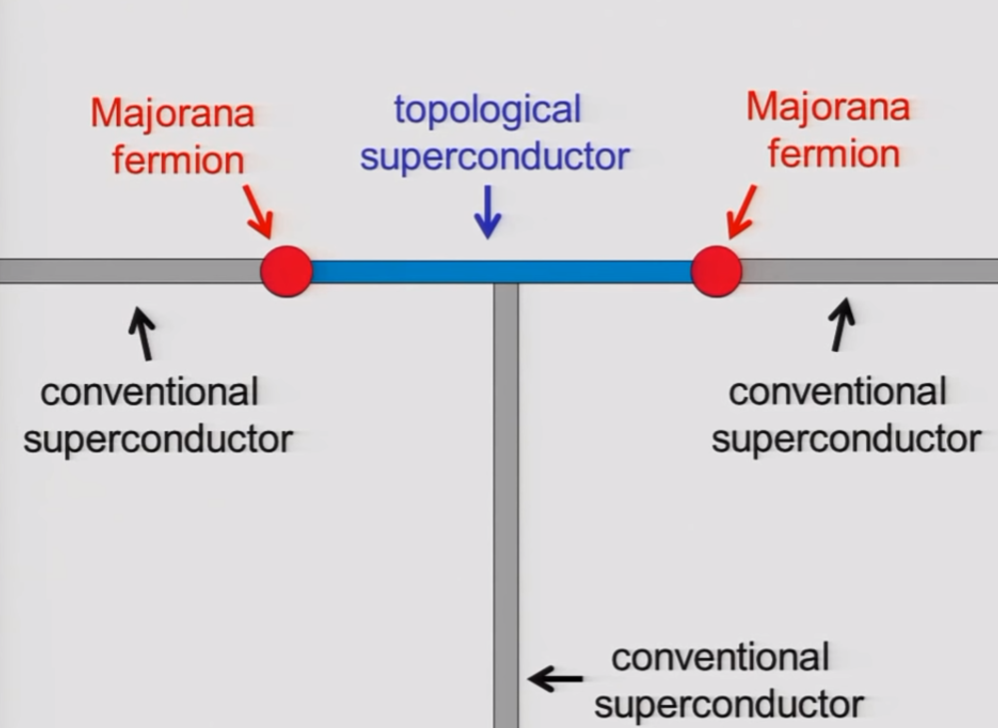
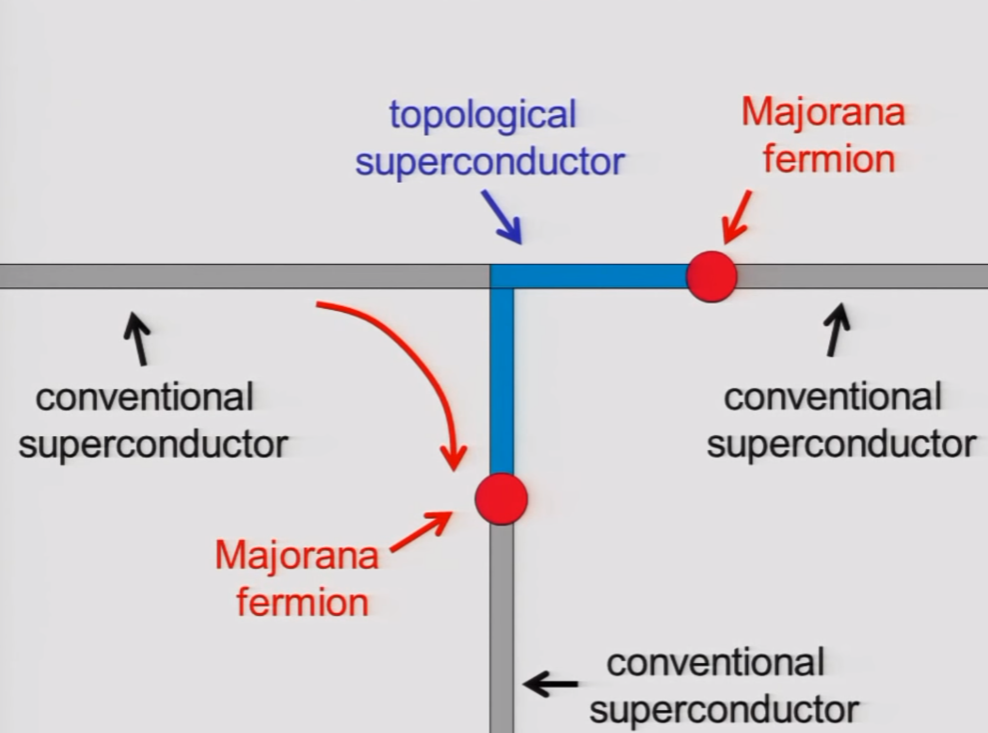
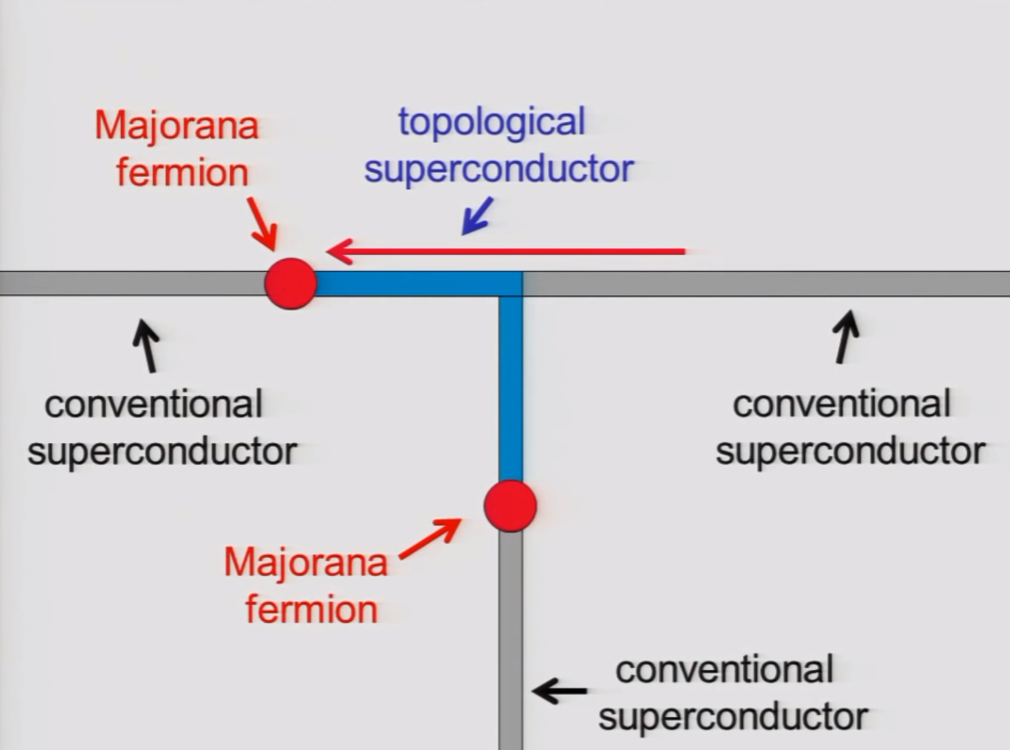
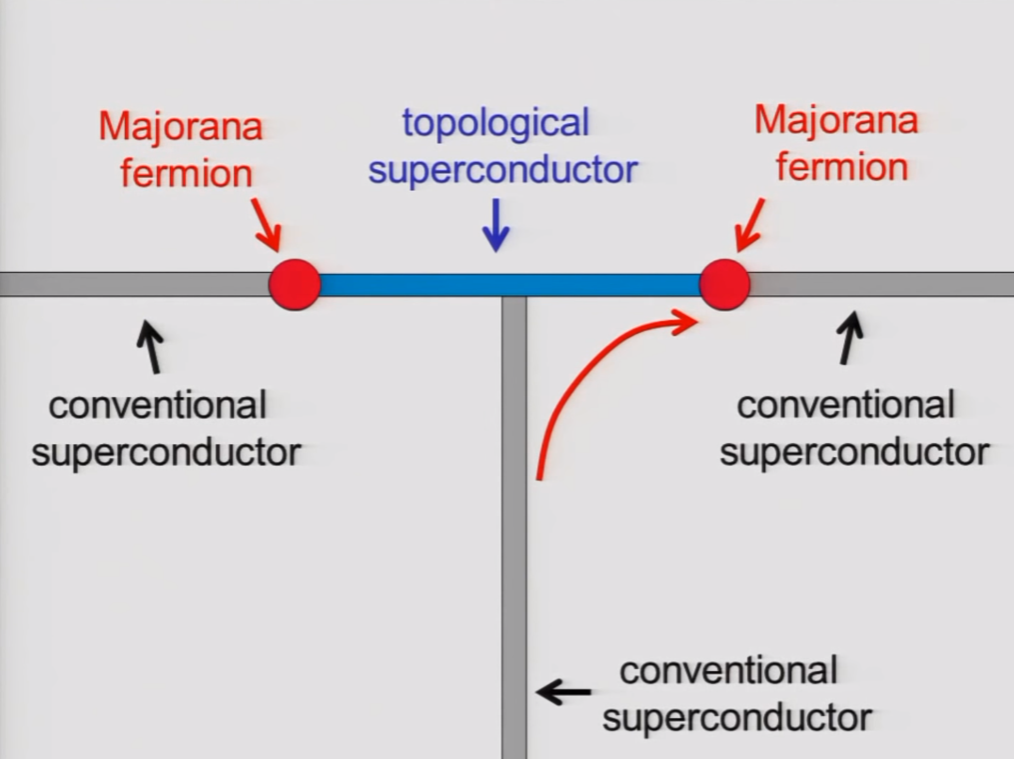
(Topological Quantum Computer - Professor John Preskill, Caltech, YouTube)
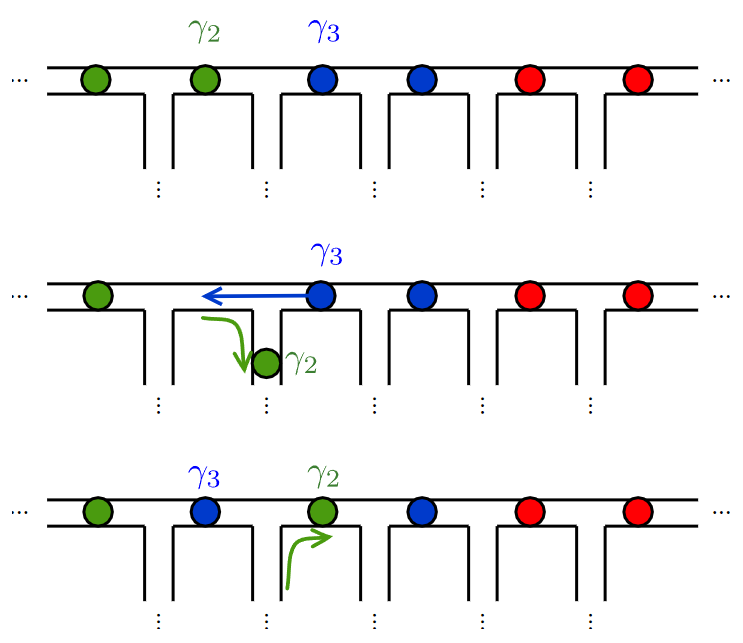
We can do quantum gates by braiding the Majoranas.
Great quantum memory!
You and your buddy were made in a pair,
Then wandered around, braiding here, braiding there.
You'll fuse back together when braiding is through
Well bid you adieu as you vanish from view.
Alexei exhibits a knack for persuading
That someday we'll crunch quantum data by braiding, With quantum states hidden where no one can see, Protected from damage through topology.
Anyon, anyon, where do you roam?
Braid for a while ... before you go home.
John Preskill
Classification of Topological Superconductors
Bulk-edge correspondence
Topological Phases
Holes
Topological quantum computation
References
[1]Topology in Condensed Matter Course (Main reference)
[2]M. Leijnse and K. Flensberg, Introduction to Topological Superconductivity and Majorana Fermions, Semicond. Sci. Technol. 27, 124003 (2012).
[3]C. W. J. Beenakker, Search for Majorana Fermions in Superconductors, Annu. Rev. Condens. Matter Phys. 4, 113 (2013).
[4]B. Field and T. Simula, Introduction to Topological Quantum Computation with Non-Abelian Anyons, Quantum Sci. Technol. 3, 045004 (2018).
Topology in physics
By Zhi Han
