Superconducting Qubits in 1 hour

Based off the CMC Superconducting Qubits Workshop

Zhi Han

Overview

  • Review of superconductivity
  • The LC Circuit
  • The Josephson effect
  • Transmons
    • Jaynes-Cumming Hamiltonian
  • SQUIDs

Main goal is give an overview to superconductors and provide reference

What is a superconductor?

 

  • Meissner effect
  • Zero resistivity under \(Tc\)
  • Cooper pairs
  • One macroscopic wavefunction

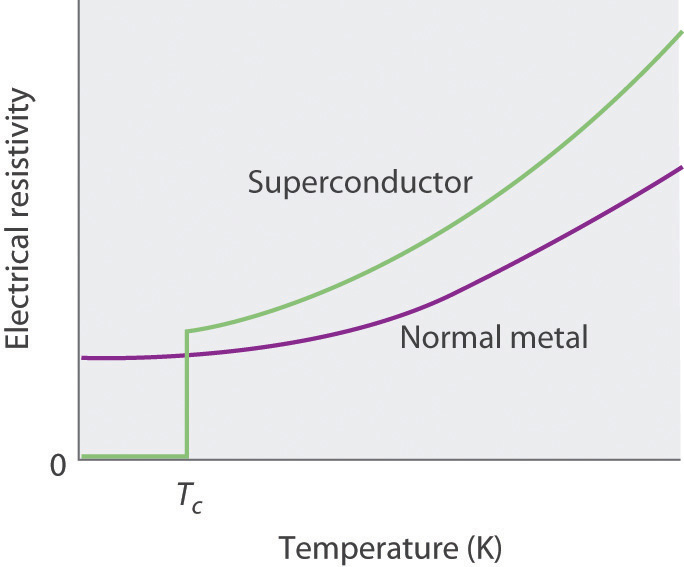
Image: Reddit

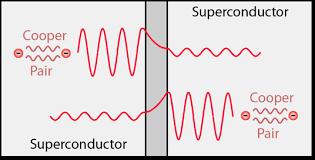
Cooper pairs

  • Electrons pair up to form cooper pairs.
  • These cooper pairs behave as bosons rather than photons.
  • Bosons do not obey the Pauli exclusion principle.
  • Therefore, all the cooper pairs can simultaneously occupy the ground state, and behave as one wavefunction.
  • We will make this ansatz later: \[ \psi = \sqrt{n}e^{i\varphi}\]

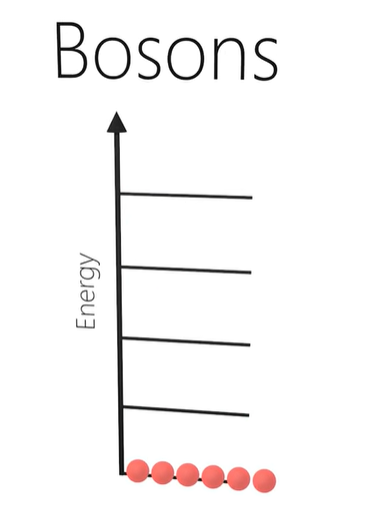
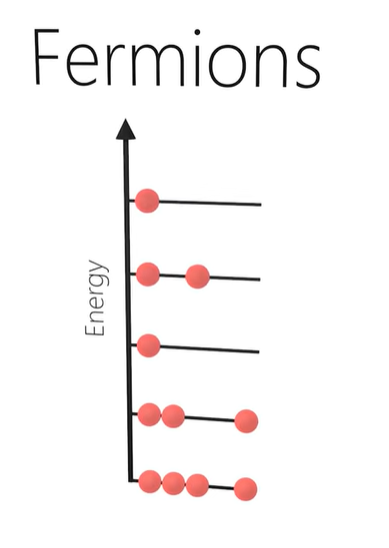
Image: Higgsino Physics

\displaystyle
\displaystyle

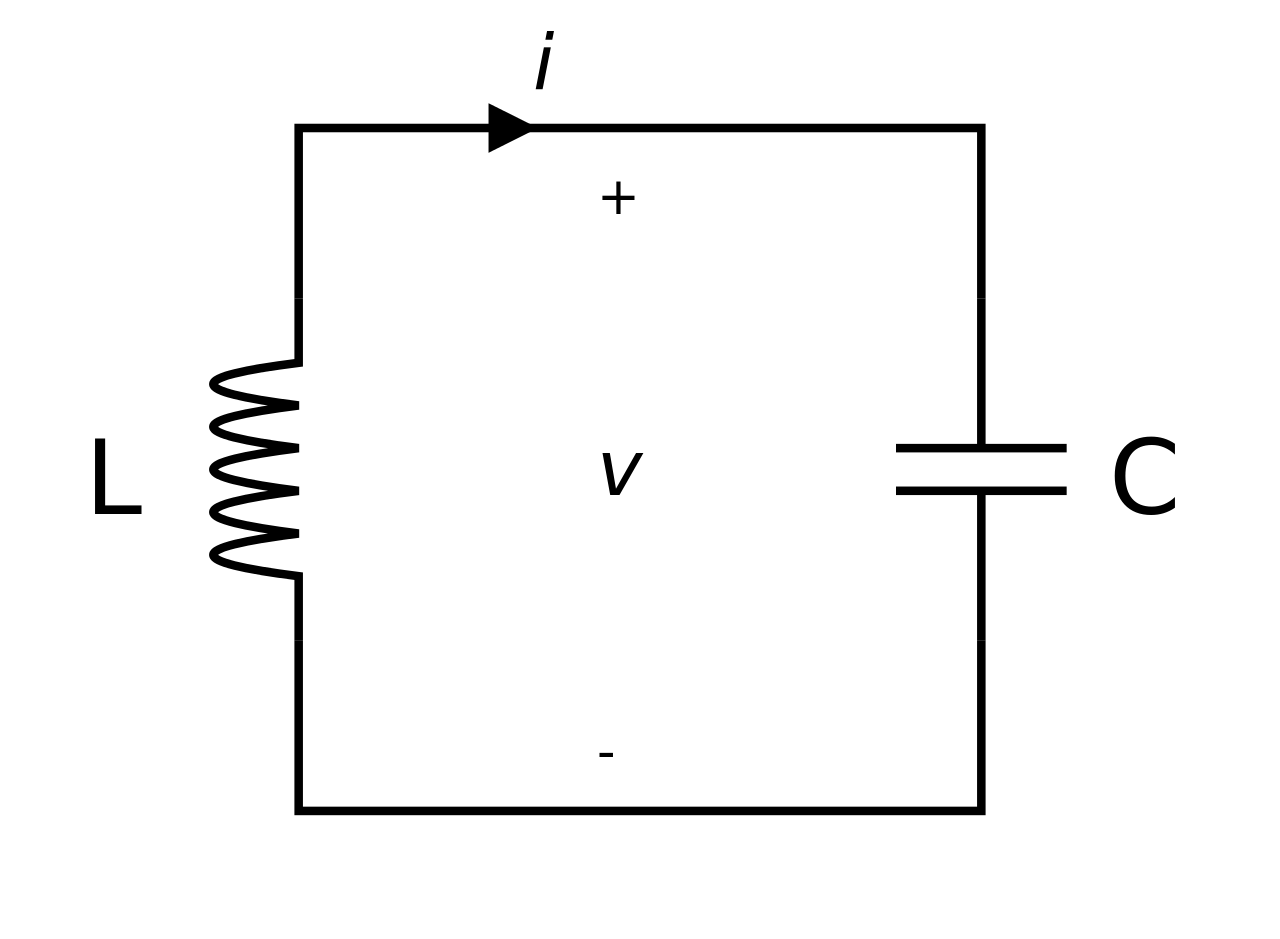
LC Circuit

\omega_r = \frac{1}{\sqrt{LC}}
\displaystyle

Looks like SHO:

\[E=\frac{1}{2}m\omega^2x^2 + \frac{1}{2}m\dot{x}^2\]

Total energy:

\[ E_m + E_e = \frac{1}{2}C\omega_r^2\Phi^2(t) + \frac{1}{2}C\dot{\Phi}^2(t)\]

x \to \Phi, m \to C

LC Circuit

Image: Wikipedia - LC Circuit

\omega_r = \frac{1}{\sqrt{LC}}
E_m = \frac{1}{2L} \Phi^2(t) = \frac{1}{2}C\omega_r^2 \Phi^2(t)
E_e = \frac{1}{2} C V(t)^2 = \frac{1}{2}C\dot{\Phi}^2(t)

Electric and Magnetic Energy

Lagrangian Formulation

\displaystyle
\displaystyle
\displaystyle \mathcal{L} = E_e - E_m = \frac{1}{2}C\dot{\Phi}^2(t) -\frac{1}{2}C\omega_r^2\Phi^2(t)
\begin{gathered} \frac{d}{d t} \frac{\partial \mathscr{L}}{\partial \dot{\Phi}}-\frac{\partial \mathscr{L}}{\partial \Phi}=0 \end{gathered}
\implies \ddot{\Phi}(t)+\omega_{r}^{2} \Phi(t)=0
\Phi(t) = \Phi_0 \cos(\omega_r t)

Solution

\frac{d}{d t} \frac{\partial \mathscr{L}}{\partial \dot{\Phi}}=C \ddot{\Phi} \\ \frac{\partial \mathscr{L}}{\partial \Phi}=\frac{1}{L} \Phi

Euler Lagrange Equations

Equation of motion

\omega_r = \frac{1}{\sqrt{LC}}
\displaystyle
\displaystyle
\displaystyle Q=\frac{\partial\mathscr{L}}{\partial\dot{\Phi}}=C \dot{\Phi}

Conjugate momentum

to flux is charge

E_m = \frac{1}{2L}\Phi^2(t) = \frac{1}{2L}\Phi_0 \cos^2(\omega_rt)
E_e = \frac{C}{2}\dot{\Phi}^2(t) = \frac{1}{2L}\Phi_0^2\sin^2(\omega_r t)
E_t = \frac{1}{2L}\Phi^2_0

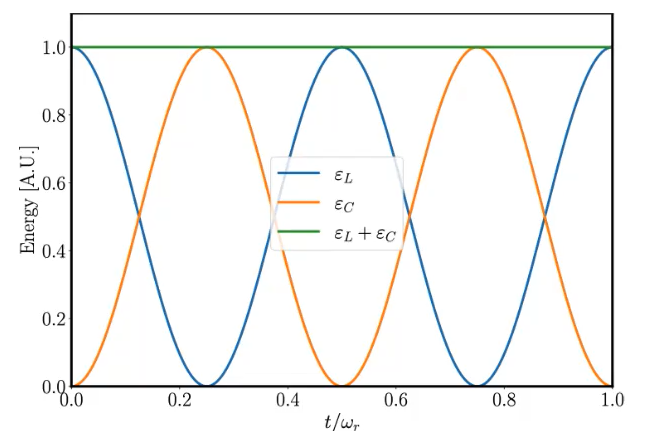
Oscillating between electric and magnetic

LC Hamiltonian

H_{L C}=Q \dot{\Phi}-\mathscr{L}=\frac{1}{2 C} Q^{2}+\frac{1}{2 L} \Phi^{2}

Promote flux and charge to quantum operators (canonical/dirac quantization)

\{A,B\} \longmapsto \tfrac{1}{i \hbar} [\hat{A},\hat{B}]

Since flux and charge are already canonical coordinates we just promote

\hat H_{L C} = \frac{1}{2 C} \hat Q^{2}+\frac{1}{2 L} \hat \Phi^{2}
[\hat \Phi, \hat Q] = i\hbar

LC Hamiltonian

\hat H_{L C} = \frac{1}{2 C} \hat Q^{2}+\frac{1}{2 L} \hat \Phi^{2}
\hat{\Phi}=\Phi_{z p f}\left(\hat{a}^{\dagger}+\hat{a}\right) \quad \hat{Q}=i Q_{z p f}\left(\hat{a}^{\dagger}-\hat{a}\right)
\hat{H}_{L C}=\hbar \omega_{r}\left(\hat{a}^{\dagger} \hat{a}+1 / 2\right)
\begin{aligned} \Phi_{z p f} &=\sqrt{\hbar Z_{r} / 2} \\ Q_{z p f} &=\sqrt{\hbar / 2 Z_{r}} \end{aligned}

Original Hamiltonian

Raising/lowering operators

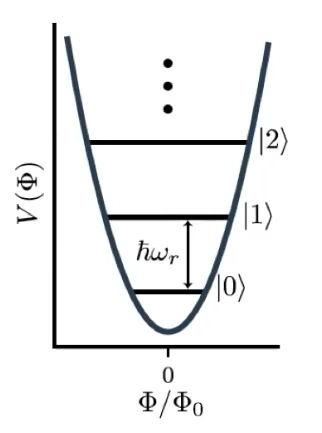
LC circuit as QHO

  • Eigenstates of LC circuit satisfies \( a^\dagger a | n \rangle = n |n\rangle \)
  • \(a^\dagger \) creates a quantized excitation of flux and charge. In other words, a photon of frequency \( \omega_r\) is created.

Coplanar waveguide

Resonant Modes

Transmission line LC circuit

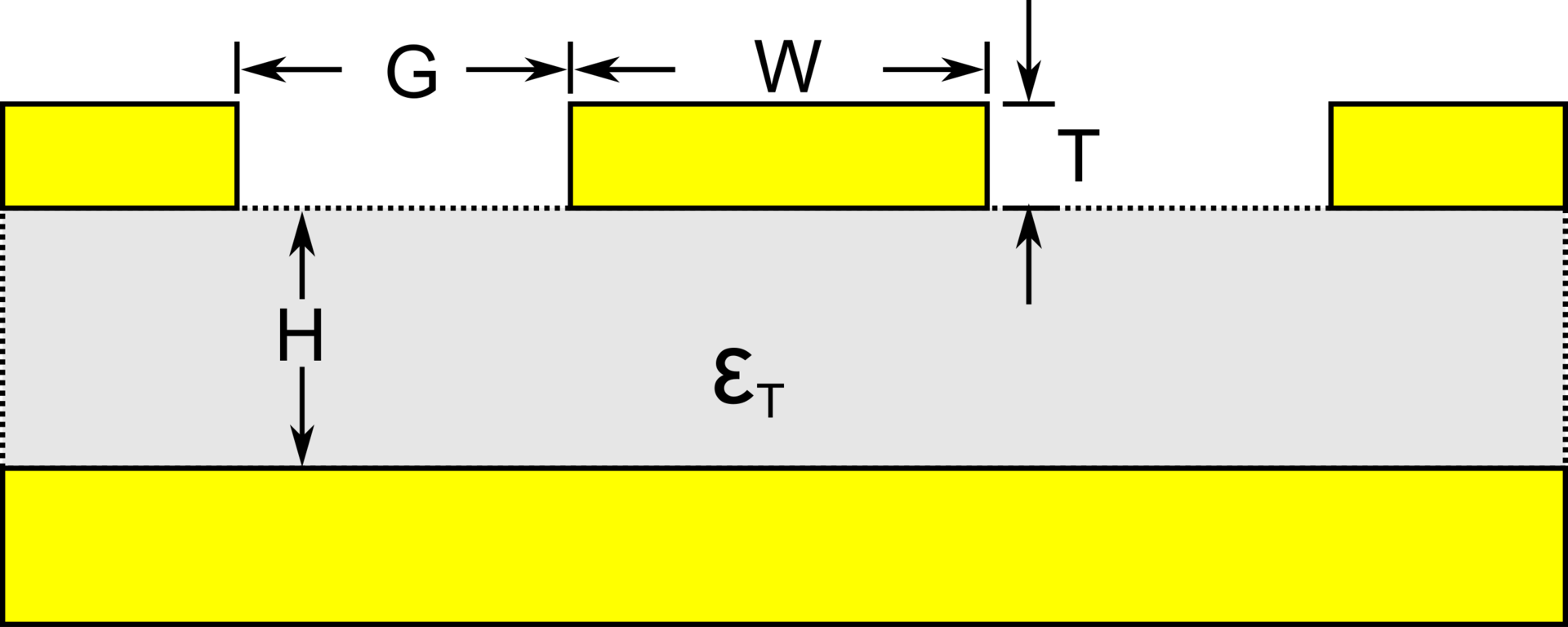
Conductors

Dielectric

Coplanar Waveguides

  • Transmission line.
  • Behave as coupled LC circuits.
  • The solution for a chain of 1d harmonic oscillators is given by a wave equation.
  • Described by the Telegrapher's equations.
\displaystyle \frac{\partial^2 V}{{\partial t}^2} - u^2 \frac{\partial^2 V}{{\partial x}^2} = 0
\displaystyle \frac{\partial^2 I}{{\partial t}^2} - u^2 \frac{\partial^2 I}{{\partial x}^2} = 0
u = \frac{1}{\sqrt{LC}}

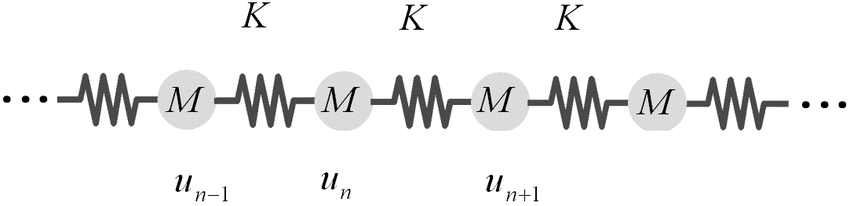
Images: Wikipedia

SC Device Physics Function in SC circuit
LC circuit/Resonator Quantum Harmonic Oscillator Readout, control, couple qubits.
Coplanar Waveguide Telegrapher's Equations Transmission of qubits as photons
Josephson Junction Josephson's Equations Nonlinear inductor
SQUID Josephson's Equations, Two state system Qubit (Magnetic flux)
Transmon Two state system Qubit (Charge)
Transmon with LC circuit Jaynes-Cumming Hamiltonian Qubit (Charge)

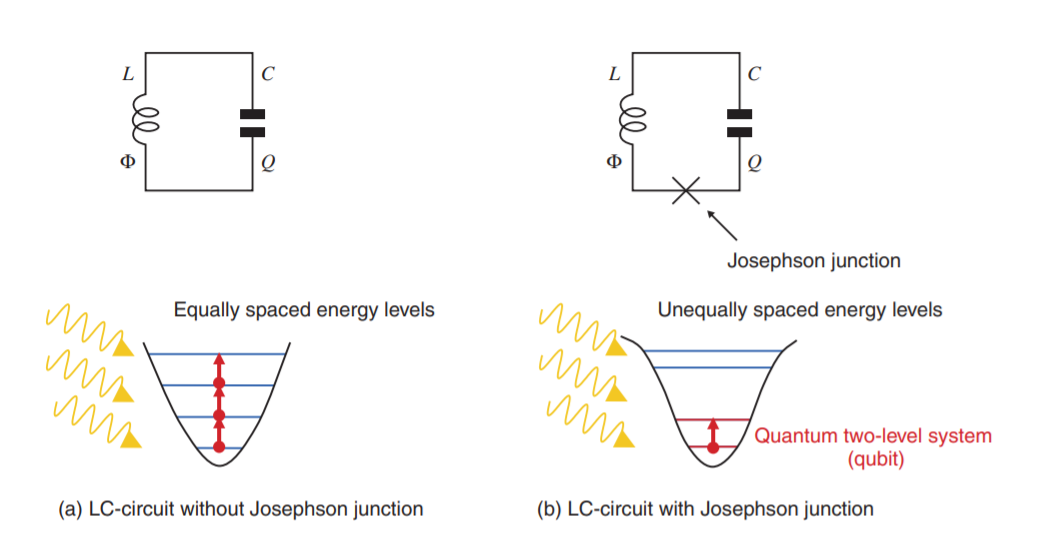
Josephson Junctions

  • LC circuit is a linear device that cannot be used for a qubit. But it is used for readout, control, and couple qubits.
  • Non-linearity is needed to process and encode quantum information.
  • Superconducting qubits and quantum parametric amplifiers are possible only with a non linear element.

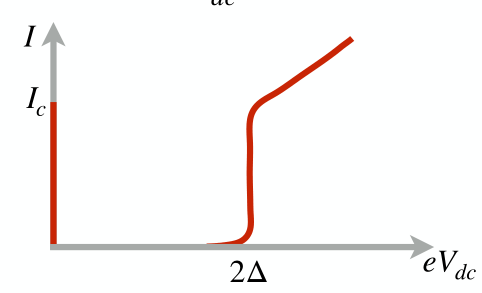
Josephson Relations

  • Obtained by solving the Schrodinger equation with the ansatz \[ \psi = \sqrt{n}e^{i\phi}\] on both sides of the junction.
\boxed{{\displaystyle I(t)=I_{c}\sin(\varphi (t))}}
\boxed{{\displaystyle {\frac {\partial \varphi }{\partial t}}={\frac {2eV(t)}{\hbar }}}}
\varphi=2 \pi \Phi / \Phi_{0} = \phi_2 - \phi_1
\Phi_{0}=h / 2 e

Josephson Phase

Quantum flux

Worth memorizing!!!!

{\displaystyle I(t)=I_{c}\sin(\varphi (t))}
L_{J}=\left(\frac{\partial I}{\partial \Phi}\right)^{-1}=\frac{\Phi_{0}}{2 \pi I_{c}} \frac{1}{\cos \left(2 \pi \Phi / \Phi_{0}\right)}

Josephson current equation

Non-linear inductor

Linear inductor

I = \Phi/L
\begin{aligned} \varepsilon_{J J}(t) &=\int V\left(t^{\prime}\right) I\left(t^{\prime}\right) d t^{\prime}=\int \frac{d \Phi\left(t^{\prime}\right)}{d t^{\prime}} I_{c} \sin \left(2 \pi \Phi / \Phi_{0}\right) d t^{\prime} \\ &=\boxed{-E_{J} \cos \left(2 \pi \Phi / \Phi_{0}\right)} \end{aligned}

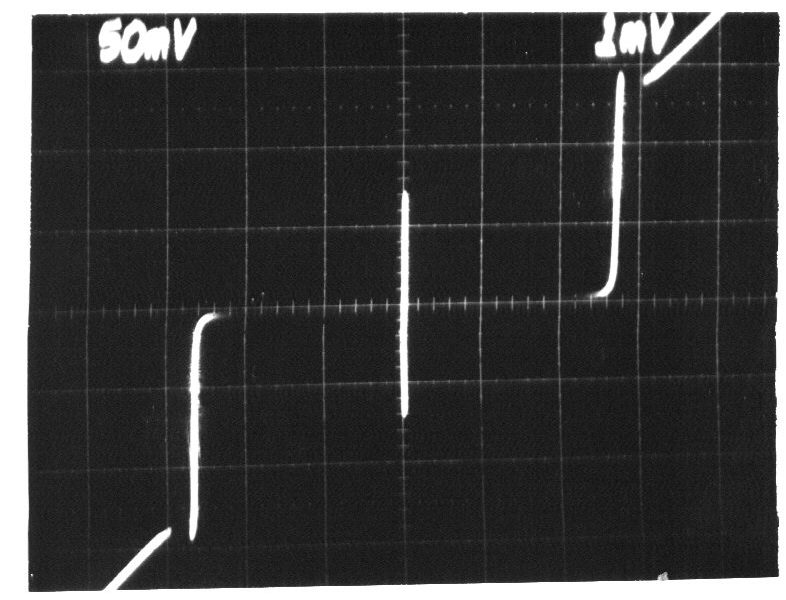
Energy of a Josephson Junction

E_{J}:=\Phi_{0} I_{c} / 2 \pi

Archetype 1:

Transmon Qubit

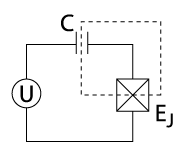
Transmon Qubit

  • Replace linear inductor with a Josephson Junction.
\mathcal{L}=\frac{C_{\Sigma}}{2} \dot{\Phi}^{2}(t)+E_{J} \cos \left(2 \pi \Phi / \Phi_{0}\right)
\hat{H}=\frac{1}{2 C_{\Sigma}}\left(\hat{Q}-Q_{g}\right)^{2}-E_{J} \cos \left(2 \pi \hat{\Phi} / \Phi_{0}\right)
C_\Sigma = C_j + C_c
[\hat{Q}, \hat{\Phi}]=i\hbar
H = Q\dot{\Phi} - \mathcal{L}

Quantization

Hamiltonian of a Transmon

Transmon Qubit

Image Source

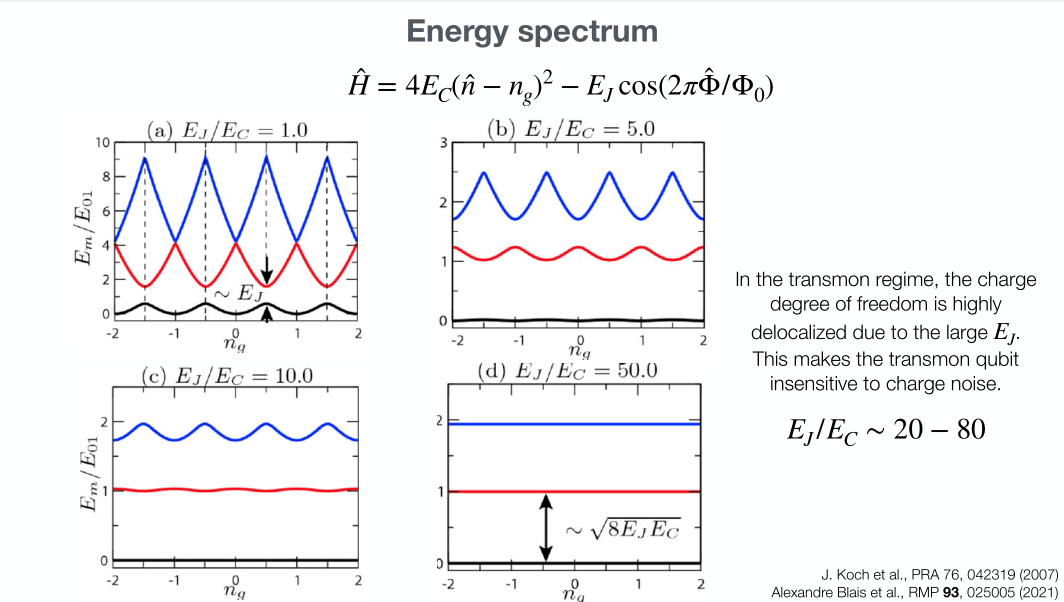
LC-Transmon Hamiltonian

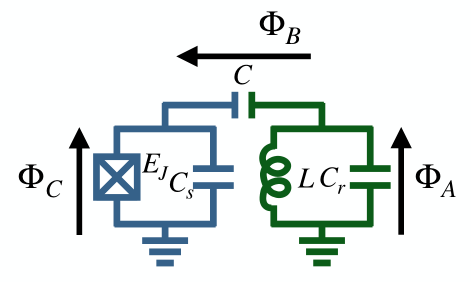
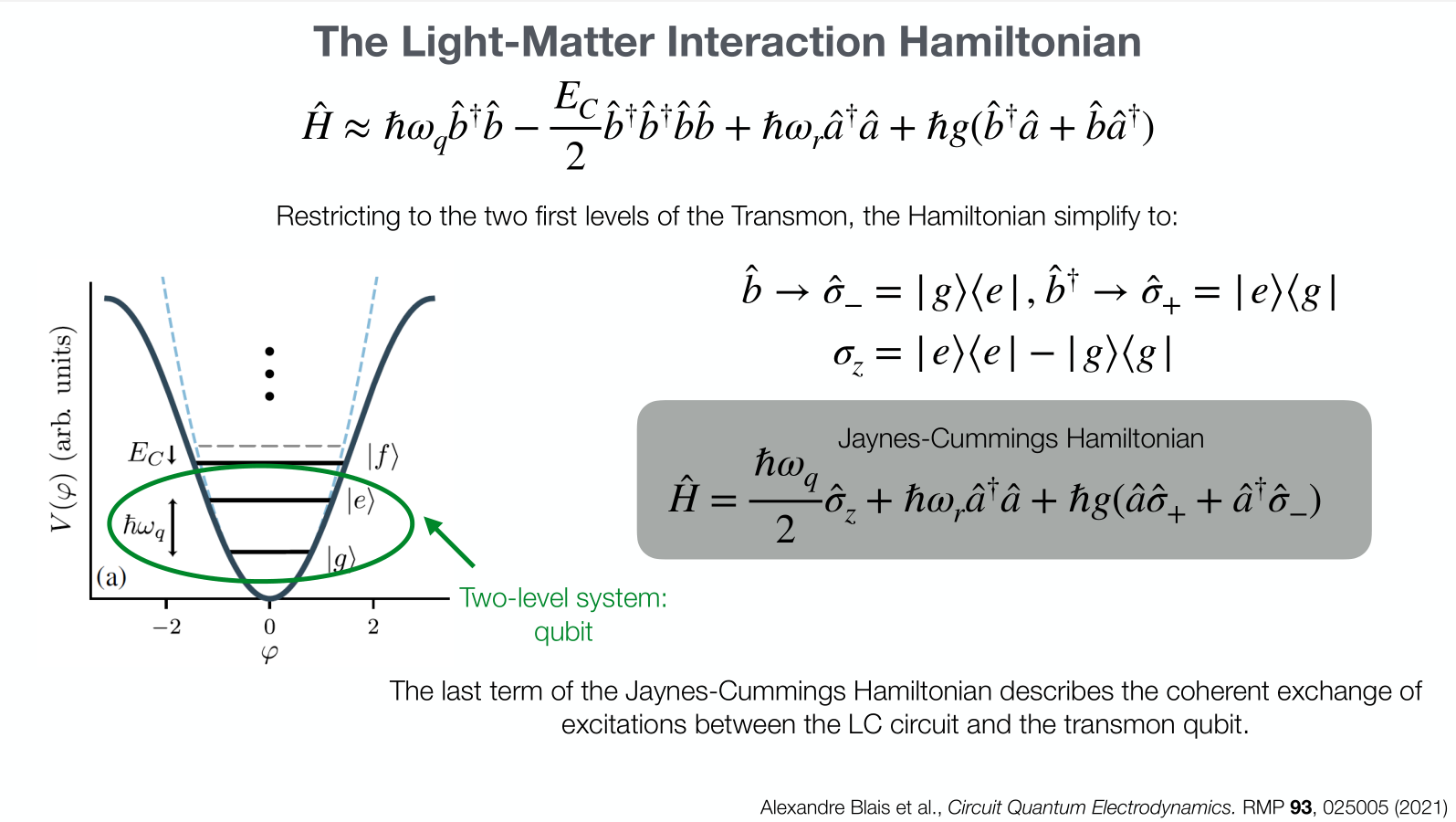
  • Transmon coupled with LC circuit.
  • Solving this circuit results in the Jaynes-Cumming Hamiltonian.
  • Qubit readout commutes with the Hamiltonian, so we don't disturb the state.
  • Interaction is mediated by virtual photons.

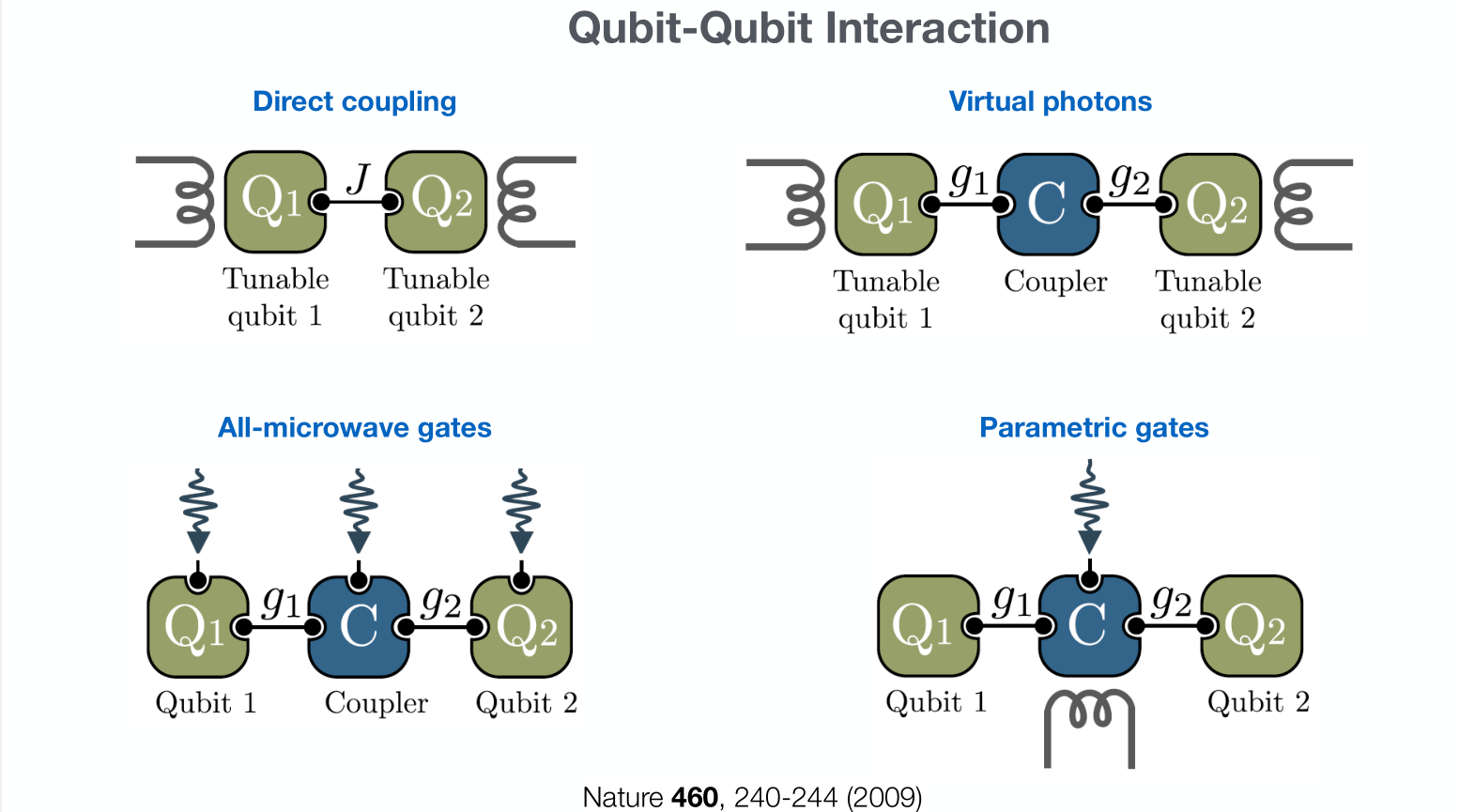
Archetype 2: SQUID Qubits

SC Device Physics Function in SC circuit
LC circuit/Resonator Quantum Harmonic Oscillator Readout, control, couple qubits.
Coplanar Waveguide Telegrapher's Equations Transmission of qubits as photons
Josephson Junction Josephson's Equations Nonlinear inductor
SQUID Josephson's Equations, Two state system Qubit (Magnetic flux)
Transmon Two state system Qubit (Charge)
Transmon with LC circuit Jaynes-Cumming Hamiltonian Qubit (Charge)

Superconducting loop

\psi(z)=m_{s} e^{i \theta(z)}, z \in[0,2 \pi R)
\frac{1}{2 m^{*}}\left(\frac{\hbar}{i} \nabla-q^{*} \vec{A}\right)^{2} \psi \approx 0

Ginzburg-Landau

\Phi
\implies \frac{1}{2 m^{*}} \frac{\hbar}{i} \nabla \cdot \frac{\hbar}{i} \vec{\nabla} \cdot\left[\psi_0(r) e^{\frac{-iq^{*}}{\hbar} \int_{0}^{z} \mathbf{A} \cdot d \mathbf{l}}\right] \approx 0
\psi(z)=n_{s} e^{\frac{iq^*}{\hbar}\int_0^z\mathbf{A} \cdot d \mathbf{l}}
\Phi = LI_s + \Phi_{ext}

Internal flux

External flux

Source: Wikipedia

Superconducting loop

\Phi
\psi(z=0) = \psi(z=2\pi R)

Periodic boundary conditions

\psi(z)=n_{s} e^{\frac{iq^*}{\hbar}\int_0^z\mathbf{A} \cdot d \mathbf{l}}
\implies n_s=n_{s} e^{\frac{iq^*}{\hbar}\oint_0^z\mathbf{A} \cdot d \mathbf{l}}=n_{s} e^{\frac{iq^*}{\hbar}\Phi}
1 = e^{\frac{-q^*\Phi}{\hbar}} \implies \frac{q^*\Phi}{\hbar} = 2 \pi m, m\in \Z
\frac{\Phi}{2 \pi\hbar/q} = m \implies \boxed{\Phi/\Phi_0 =m}

Flux is quantized

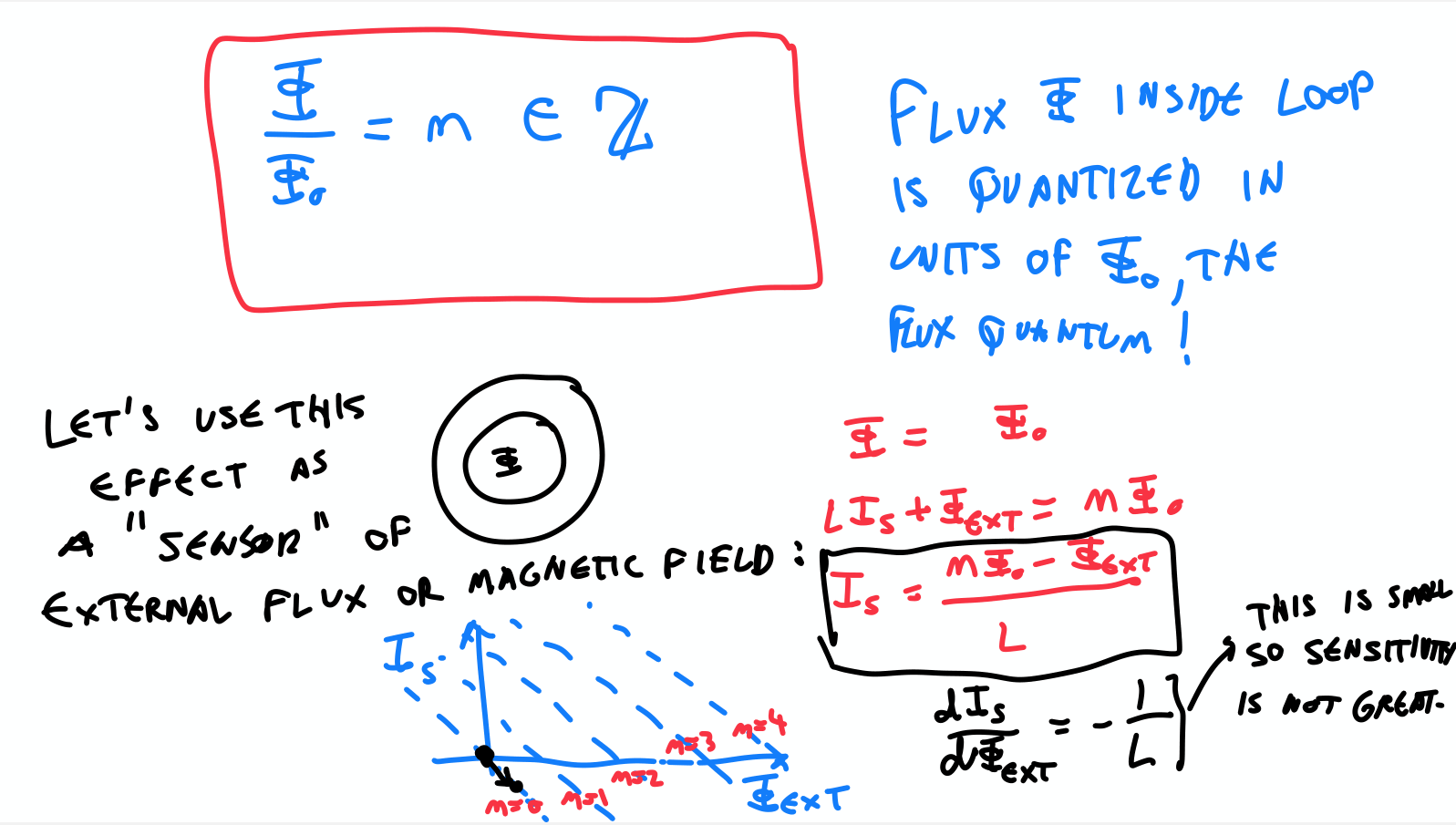
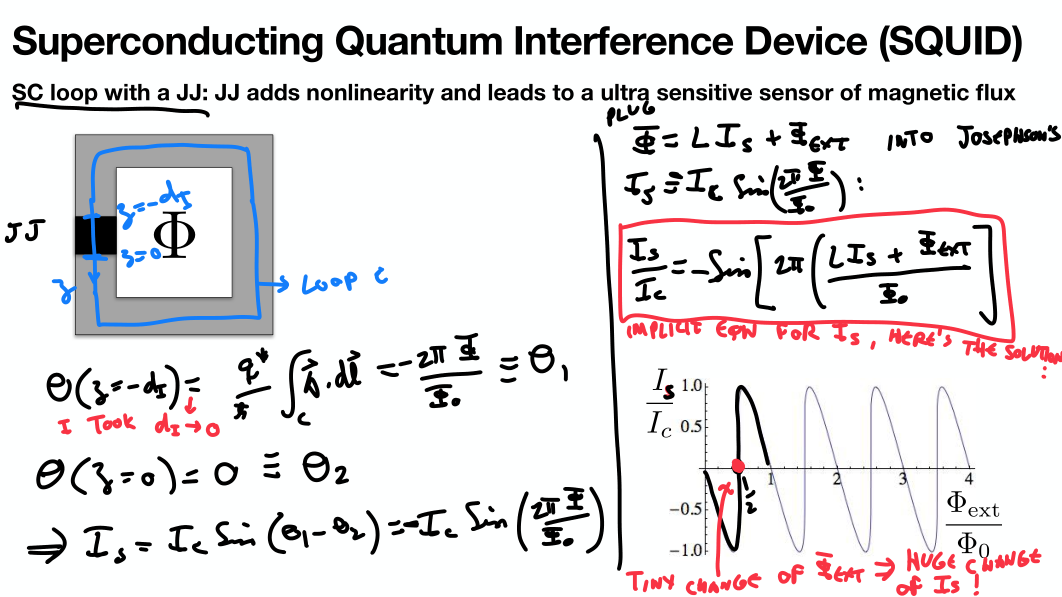
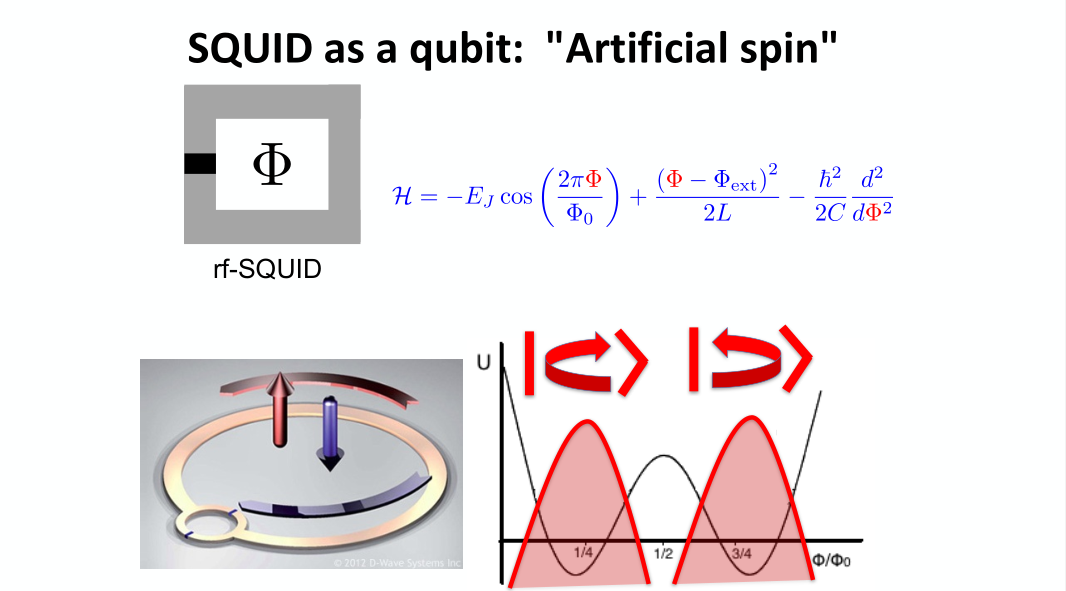
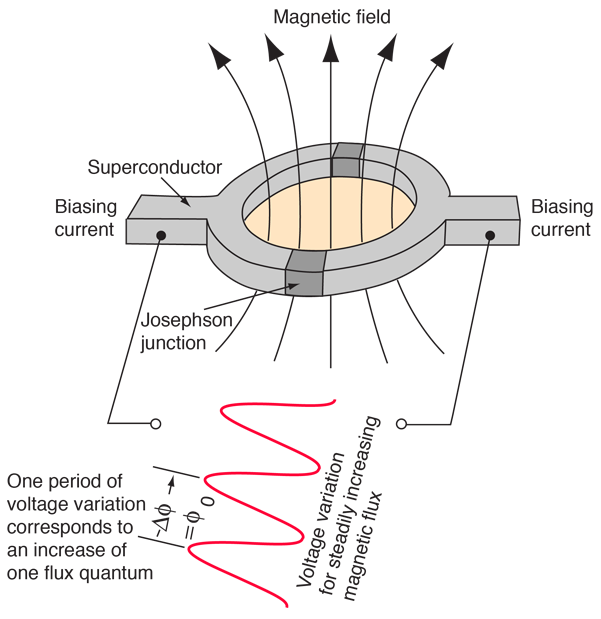
  • A small change in the external magnetic field changes the current.
  • Used as qubit or quantum sensor.
  • Based on the idea that flux is quantized.

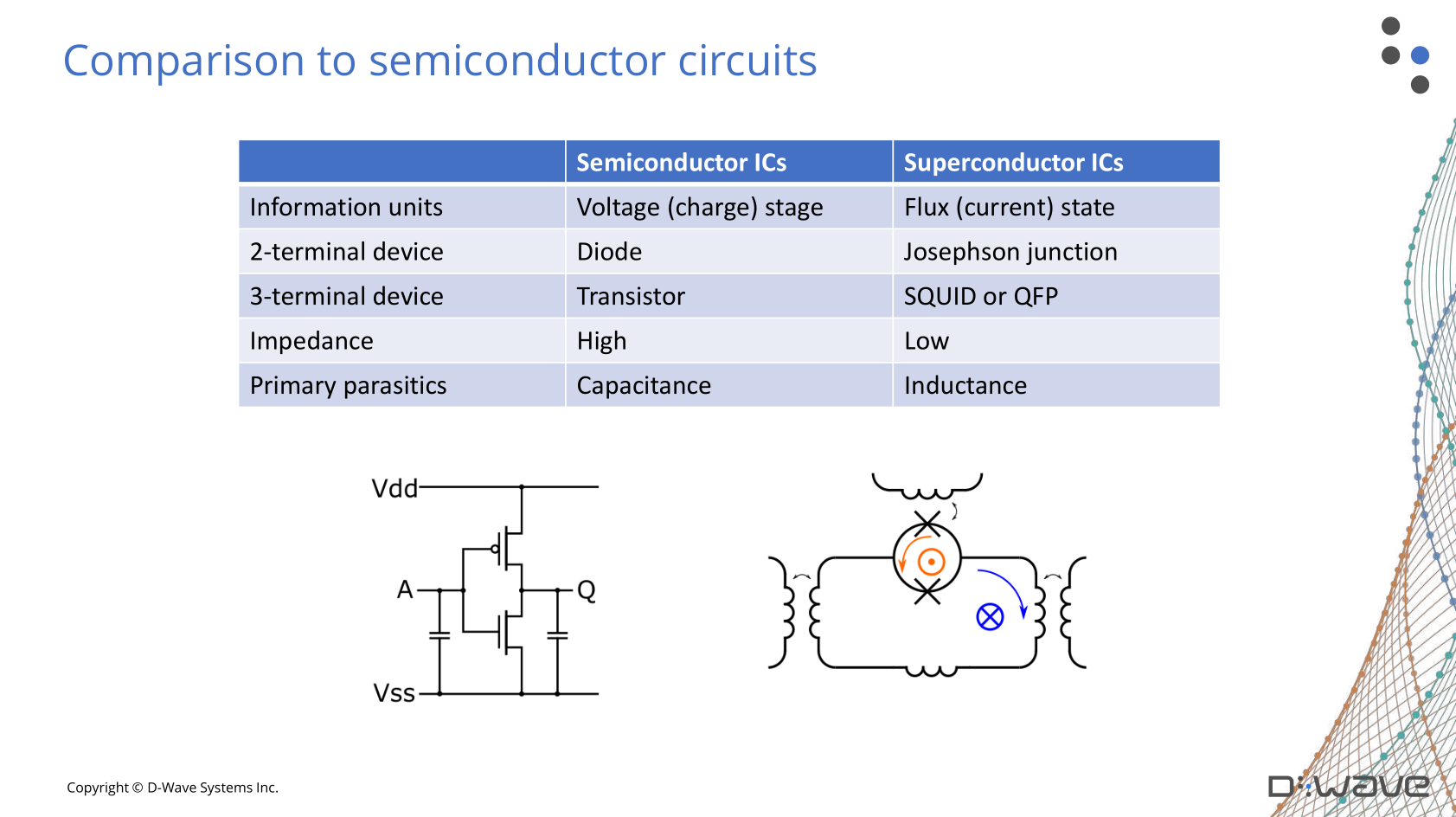
(D-Wave slides)

Further Reading on Transmons

  • Circuit Quantum Electrodynamics, Alexander Blais 
    • arXiv:2005.12667 [quant-ph]
  • Udson C. Mendes slides from Cornerstones of Quantum Computing Workshop

Questions

superconducting

By Zhi Han

superconducting

  • 163

More from Zhi Han