時間複雜度

講師蕭梓宏

極粗略課程大綱

甚麼是時間複雜度？
時間複雜度對我(你)來說很重要嗎？
怎麼估複雜度？

針對這堂課的提醒

雖然是遠距上課，但還是希望大家能有多一點互動
- 有想法就可以提出來
課程內容的難易度未必適合所有人
- 有問題就問
- 覺得太簡單不用急，後面的講師一定可以滿足你
雖然這堂課可能偏理論，但並非那麼嚴謹

什麼是時間複雜度？

某個演算法的時間複雜度？

一個描述該演算法(或程式)執行時間的函式
通常假設各種基本操作都花一單位時間
- 加、減、乘、除、取模
- 賦值
- 條件判斷
- 存取變數
- …...

舉例

\(F(N) = N^2+2N+3\)

cin >> N;
i = 0;//1
j = 0;//1
while(i < N)//N+1
{
    while(j < i)//1+2+3+..+N=(N+1)N/2
    {
        j++;//1+2+3+..+(N-1)=(N-1)N/2
    }
    i++;//N
}

這個算起來也太麻煩了吧

big-O

\(f(x) = O(g(x))\) 代表存在\(M,x_0 > 0\)，使得所有\(x \geq x_0\)都有\(|f(x)|\leq M|g(x)|\)
也就是說，當\(x\)很大的時候，存在常數\(M\)，使得\(M|g(x)|\)一定會大於等於\(f(x)\)
其實也就表示，\(g(x)\)是\(f(x)\)的某種上界
看例子！

例子

\(f(x)\)

\(g(x)\)

\(f(x) = O(g(x))\)？

\(x\)

\(100x\)

Yes

\(x\)

\(100x\)

Yes

\(x^3\)

\(x^2\)

\(\frac{x^2\log(x)}{10000}\)

Yes

\(x-1000\sqrt{x}-100\)

\(x\)

big-O

可以看出，只要有了big-O符號，我們就可以無視低次項跟常數，更方便地表示複雜度
因此，在剛剛的例子中，原本複雜度是
\(F(N)=N^2+N+4\)，現在也可以用\(O(N^2)\)來表示該程式的時間複雜度
雖然也可以用\(O(N^3)\)來表示，但我們追求的是複雜度越小越好！
這樣估複雜度就不用那麼麻煩了！

小測驗

\(O(N^3)\)

cin >> N;
i = 0;
j = 0;
while(i < N*N+N-2)
{
    while(j < N*3-10)
    {
        j++;
    }
    i++;
}

小測驗

\(O(N^2\sqrt{N})\)

cin >> N;
i = 0;
j = 0;
while(i < N*N+N-2)
{
    while(j*j < N)
    {
        j++;
    }
    i++;
}

時間複雜度很重要嗎？

很重要

即使你的程式是正確的，如果他的執行時間超過了題目的限制，你會得到一個而無法得到分數
一般的judge一秒可以跑\(10^8\)筆運算左右，所以想要知道自己的程式會跑幾秒，就把題目的範圍限制代入所估的複雜度中，最後再除以\(10^8\)。然後再跟題目的限制秒數比比看就可以知道會不會TLE了
注意我們要估的通常是最糟的情形

第一個例題！

給定一個單字，請你找出其中"最長的"連續的一段，使得那段正著唸反著唸都一樣。(單字長度\(L \leq 5000\))

範例輸入：

abcbbd

範例輸出：

bcb

作法其一

枚舉所有的「連續的一段」，再把那一段掃過一遍就好囉！

abac

作法其一複雜度

因為長度為\(1\)的區間有\(L\)個，\(2\)的區間有\(L-1\)個，...，\(L\)的區間有\(1\)個，所以複雜度是\(1\times L+2\times (L-1)+...+L\times 1=\frac{L^3+3L^2-4L}{6}\)

複雜度是：

枚舉連續的一段 \(O(L^2)\)

然後再把那段掃一遍最糟\(O(L)\)

所以就是\(O(L^3)\)囉！

這樣OK嗎?

已知\(L \leq 5000\)，而複雜度為\(L^3\)
\(5000^3=1.25\times 10^{11} >> 10^8\)

跑100秒都跑不完QQ

作法其二

枚舉所有的「中間點」，然後看可以往外擴張多少！

作法其二

枚舉所有的「中間點」，然後看可以往外擴張多少！

a b c b b d

長度：3

作法其二

枚舉所有的「中間點」，然後看可以往外擴張多少！

a b c b b d

長度：2

作法其二複雜度

複雜度是：

枚舉中間點(包含中間字母語中間空隙) \(O(L)\)

然後看可以往外擴張多少最糟\(O(L)\)

所以就是\(O(L^2)\)囉！

\(5000^2 = 2.5 \times 10^7\)，理論上一秒內可以跑完！

第一個例題實作時間

回文好玩好文回(6)

10 min

複雜度真的很重要

除了判斷自己的演算法可不可以拿到想要的分數之外，因為比較難的題目通常都會把限制的範圍出的盡量大，所以看到範圍後也可以得到一些關於作法複雜度的線索

第二個例題！

給你一個正整數\(Q\)，接下來有\(Q\)筆詢問，每次詢問你一個整數\(N\)是不是質數。

範例輸入：

\(3\)

\(1\)

\(2\)

\(3\)

範例輸出：

Yes

第二個例題！版本一

給你一個正整數\(Q\)，接下來有\(Q\)筆詢問，每次詢問你一個整數\(N\)是不是質數。

範圍：\(Q\leq 100\)，\(N\leq 10^{10}\)

第二個例題！版本二

給你一個正整數\(Q\)，接下來有\(Q\)筆詢問，每次詢問你一個整數\(N\)是不是質數。

範圍：\(Q\leq 10^6\)，\(N\leq 10^6\)

版本一 \(Q\leq 100\)，\(N\leq 10^{10}\)

這個版本的\(Q\)範圍比第二個版本小，所以我們每筆詢問的複雜度把\(N\)帶入後不超過\(\frac{10^8}{100}=10^6\)就好，所以每一筆詢問可以相對暴力地回答

說到最直接判斷質數的方法

試除法？

試除法複雜度

跟我們平常用手算一樣，試除法有一個重點是如果\(N\)是合數，他至少有一個因數\(d\leq\sqrt{N}\)
換句話說，我們只要拿\(2,3,..., \left \lfloor{\sqrt{N}}\right \rfloor\)這\(O(\sqrt{N})\)個東西去除除看就可以確認他是不是質數了
對每筆詢問都做一樣的事，複雜度\(O(Q\sqrt{N})\)
\(Q\leq 100\)，\(N\leq 10^{10}\)帶進去算出來大概是\(10^7\)
讚讚！

第二個例題版本一實做時間

質數判斷(7)

9 min

版本二 \(Q\leq 10^6\)，\(N\leq 10^{6}\)

直接用試除法，那個複雜度應該是過不了的！
相對於上一題，這一題的突破口是\(N\)比較小
其實，我們只要知道\(1\)~\(10^6\)中每個數是不是質數就好了！

說到找出比\(K\)小的質數的方法

篩法？

篩法

1 2 3 4 5 6 7 8 9 10

11 12 13 14 15 16 17 18 19 20

這樣做的複雜度是\(\frac{K}{2}+\frac{K}{3}+\frac{K}{5}...\)

有點難估所以抓個上界：

\(\frac{K}{2}+\frac{K}{3}+\frac{K}{5}...\leq K(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{K})\)

篩法複雜度

可以學(記)起來的小引理：\(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{K} = O(log(K))\)
所以複雜度就是\(\\\frac{K}{2}+\frac{K}{3}+\frac{K}{5}...\leq K(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{K})=O(Klog(K))\)
所以我們一開始先用\(O(Klog(K))\)的時間建好\(K=10^6\)以下的質數表，並存在陣列中
然後每筆詢問\(N\)直接\(O(1)\)去看陣列中第\(N\)格
總複雜度\(O(Klog(K)+Q);K=10^6, Q\leq 10^6\) 讚讚！

第二個例題版本二實作時間

質數判斷2(11)

9 min

第二個例題！

所以，除了題目本身之外，也要根據範圍來選擇適合的做法！

\(Q\leq 100,N\leq 10^{10}\)

\(Q\leq 10^6,N\leq 10^6\)

\(O(Q\sqrt{N})\)

\(O(Klog(K)+Q)\)

TLE

有此一說(僅供參考)

如果有一題他的複雜度只跟\(N\)有關的話

範圍

做法複雜度

\(N\leq 10\)

\(O(4^N),O(N^7),O(N!),...\)

\(N\leq 20\)

\(O(N\times2^N),O(N^6),...\)

\(N\leq 50\)~ \(100\)

\(O(N^4)\)

\(N\leq 200\)

\(O(N^3log(N))\)

\(N\leq 500\)

\(O(N^3)\)

\(N\leq 2000\)

\(O(N^2log(N))\)

有此一說(僅供參考)

如果有一題他的複雜度只跟\(N\)有關的話

範圍

作法複雜度

\(N\leq 5000\)

\(O(N^2)\)

\(N\leq 5\times 10^4\)

\(O(N\sqrt{N})\)

\(N\leq 10^5\)

\(O(N\sqrt{N}),O(Nlog^2(N)),O(Nlog(N))\)

\(N\leq 10^6\)

\(O(Nlog(N)),O(N)\)

\(N\leq 10^7\)

\(O(N)\)

\(N\leq 10^{12}\)

\(O(\sqrt{N})\)

\(N\leq 10^{18}\)

\(O(log(N)),O(log^2(N)),...\)

怎麼估時間複雜度？

估時間複雜度的方法

其實大家都會了？
根據之前的例子，基本上就是看每一層迴圈最多跑多少次，然後全部乘起來？

但是......

第三個例題！

給你一個單字，你要從中找到其中連續的一段，使得該段是包含全部的字母中最短的(很多個的話請輸出最先出現的，不存在請輸出"QQ")

範例輸入：

aabbabcdefghijklmnoqrstuvwxyz

範例輸出：

abcdefghijklmnoqrstuvwxyz

某個作法

枚舉「連續的一段」的左界\(L\)，開一個26格的陣列代表每個字母出現過幾次，然後從\(L\)往右一直看直到包含所有字母為止，並記錄當前長度

假設只有三個字母(a,b,c)

a b c b a

a	b	c

\(L\)

某個作法

枚舉「連續的一段」的左界\(L\)，開一個26格的陣列代表每個字母出現過幾次，然後從\(L\)往右一直看直到包含所有字母為止，並記錄當前長度

假設只有三個字母(a,b,c)

a b c b a

a	b	c
1

\(L\)

某個作法

枚舉「連續的一段」的左界\(L\)，開一個26格的陣列代表每個字母出現過幾次，然後從\(L\)往右一直看直到包含所有字母為止，並記錄當前長度

假設只有三個字母(a,b,c)

a b c b a

a	b	c
1	1

\(L\)

某個作法

枚舉「連續的一段」的左界\(L\)，開一個26格的陣列代表每個字母出現過幾次，然後從\(L\)往右一直看直到包含所有字母為止，並記錄當前長度

假設只有三個字母(a,b,c)

a b c b a

a	b	c
1	1	1

\(L\)

長度：3

某個作法

枚舉「連續的一段」的左界\(L\)，開一個26格的陣列代表每個字母出現過幾次，然後從\(L\)往右一直看直到包含所有字母為止，並記錄當前長度

假設只有三個字母(a,b,c)

a b c b a

a	b	c

\(L\)

某個作法

枚舉「連續的一段」的左界\(L\)，開一個26格的陣列代表每個字母出現過幾次，然後從\(L\)往右一直看直到包含所有字母為止，並記錄當前長度

假設只有三個字母(a,b,c)

a b c b a

a	b	c
	1

\(L\)

某個作法

枚舉「連續的一段」的左界\(L\)，開一個26格的陣列代表每個字母出現過幾次，然後從\(L\)往右一直看直到包含所有字母為止，並記錄當前長度

假設只有三個字母(a,b,c)

a b c b a

a	b	c
	1	1

\(L\)

某個作法

枚舉「連續的一段」的左界\(L\)，開一個26格的陣列代表每個字母出現過幾次，然後從\(L\)往右一直看直到包含所有字母為止，並記錄當前長度

假設只有三個字母(a,b,c)

a b c b a

a	b	c
	2	1

\(L\)

某個作法

枚舉「連續的一段」的左界\(L\)，開一個26格的陣列代表每個字母出現過幾次，然後從\(L\)往右一直看直到包含所有字母為止，並記錄當前長度

假設只有三個字母(a,b,c)

a b c b a

a	b	c
1	2	1

\(L\)

長度：4

某個作法分析

複雜度應該蠻容易可以看出是枚舉\(L\)的\(O(N)\)乘上往右掃的\(O(N)\)，所以是\(O(N^2)\)
但是應該也有人發現其實\(L\)往右一格之後，不用從新的\(L\)開始往右掃，只要把原本\(L\)的字母出現次數減一，然後繼續掃就好

a b c b a

a	b	c

\(L\)

某個作法分析

複雜度應該蠻容易可以看出是枚舉\(L\)的\(O(N)\)乘上往右掃的\(O(N)\)，所以是\(O(N^2)\)
但是應該也有人發現其實\(L\)往右一格之後，不用從新的\(L\)開始往右掃，只要把原本\(L\)的字母出現次數減一，然後繼續掃就好

a b c b a

a	b	c
1

\(L\)

某個作法分析

複雜度應該蠻容易可以看出是枚舉\(L\)的\(O(N)\)乘上往右掃的\(O(N)\)，所以是\(O(N^2)\)
但是應該也有人發現其實\(L\)往右一格之後，不用從新的\(L\)開始往右掃，只要把原本\(L\)的字母出現次數減一，然後繼續掃就好

a b c b a

a	b	c
1	1

\(L\)

某個作法分析

複雜度應該蠻容易可以看出是枚舉\(L\)的\(O(N)\)乘上往右掃的\(O(N)\)，所以是\(O(N^2)\)
但是應該也有人發現其實\(L\)往右一格之後，不用從新的\(L\)開始往右掃，只要把原本\(L\)的字母出現次數減一，然後繼續掃就好

a b c b a

a	b	c
1	1	1

\(L\)

長度：3

某個作法分析

複雜度應該蠻容易可以看出是枚舉\(L\)的\(O(N)\)乘上往右掃的\(O(N)\)，所以是\(O(N^2)\)
但是應該也有人發現其實\(L\)往右一格之後，不用從新的\(L\)開始往右掃，只要把原本\(L\)的字母出現次數減一，然後繼續掃就好

a b c b a

a	b	c
	1	1

\(L\)

某個作法分析

複雜度應該蠻容易可以看出是枚舉\(L\)的\(O(N)\)乘上往右掃的\(O(N)\)，所以是\(O(N^2)\)
但是應該也有人發現其實\(L\)往右一格之後，不用從新的\(L\)開始往右掃，只要把原本\(L\)的字母出現次數減一，然後繼續掃就好

a b c b a

a	b	c
	2	1

\(L\)

某個作法分析

複雜度應該蠻容易可以看出是枚舉\(L\)的\(O(N)\)乘上往右掃的\(O(N)\)，所以是\(O(N^2)\)
但是應該也有人發現其實\(L\)往右一格之後，不用從新的\(L\)開始往右掃，只要把原本\(L\)的字母出現次數減一，然後繼續掃就好

a b c b a

a	b	c
1	2	1

\(L\)

長度：4

某個改進的作法

也就是說

for(L = 1;L <= N;L++)
{
    for(R = L;R <= N;R++)
    {
    	//do something
        if(something happens)
        {
            ans = min(ans,R-L+1);
            break;
        }
    }
}

int R = 1;
for(L = 1;L <= N;L++)
{
    while(R <= N) 
    {
    	//do something
        if(something happens)
        {
            ans = min(ans,R-L+1);
            //do something
            break;
        }
        R++;
    }
}

某個改進的作法分析

如果跟之前一樣看每個迴圈最多跑多少再乘起來的話，複雜度還是\(O(N^2)\)
明明感覺變快不少？

某個改進的作法分析

我們之所以把複雜想成\(O(N^2)\)，是因為我們覺得中間的while迴圈最慘會執行那麼多次

但其實可以發現，中間的while迴圈每跑一次，\(R\)就會加一，但是只有\(R \leq N\)的時候while迴圈才會執行，所以while迴圈只會執行\(O(N)\)次！

所以總複雜度其實是\(O(N)\)！

第三個例題實作時間

電皇的小寫英文字母(5)

15 min

均攤分析

有時候某個迴圈跑的數量我們不確定，就只能以最糟情況來計算複雜度
但或許我們可以想想，他總共跑的次數或許會受到某種限制
這種分析方式稱為均攤分析，通常要正確分析會需要一些經驗
剛剛例題中的演算法被稱為「雙指針」或「爬行法」，是很經典可以透過均攤分析找到真正複雜度的演算法

遞迴函式複雜度分析

如果是遞迴函式，就不能把迴圈直接乘起來囉！
但是遞迴函式也有各式各樣的，這邊就只先舉簡單的幾個例子
主定理甚麼的聽說分治那堂課會教？

送分題

int f(int n)
{
    if(n == 1) return 1;
    return n*f(n-1);
}

\(f(n)\to f(n-1) \to ... \to f(1)\)

每個函式本身都\(O(1)\)

總共\(O(n)\)！

快速冪

int Pow(int a,int b)
{
    if(n == 0) return 1;
    int t = Pow(a,b/2);
    if(b & 2 == 1) return t*t*a;
    else return t*t;
}

每個函式本身都\(O(1)\)，共有\(O(log(b))\)次函式被呼叫

總共\(O(log(b))\)！

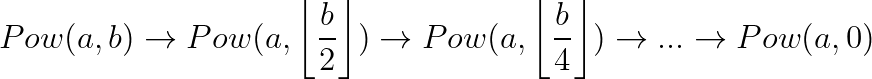
分治預習

void f(int n)
{
    if(n <= 1) return 1;
    //Do some O(n) things
    f(n/2);
    f(n/2);
}

\(f(n)\)

\(f(\left \lfloor \frac{n}{2} \right \rfloor)\times 2\)

\(f(\left \lfloor \frac{n}{4} \right \rfloor)\times 4\)

\(\cdots\)

\(f(1)\times n\)

每層都是跑\(O(n)\)

總共有\(O(log(n))\)

總複雜度\(O(nlog(n))\)！

準備下課啦

除了時間複雜度之外，也有空間複雜度
除了時間複雜度之外，還有常數
這堂課應該比接下來的課簡單，但很重要
接下來的課可能很大的比例就是在教怎麼樣才能讓複雜度降低
接下來的課一定會更有趣，講師也更強，請好好期待><

題目小整理

上課例題：

6,7,11,5

回家練習：

8,9,10

謝謝大家！

APCS Camp時間複雜度

By Zi-Hong Xiao

APCS Camp時間複雜度

APCS Camp 資料結構

時間複雜度

講師 蕭梓宏

極粗略課程大綱

針對這堂課的提醒

什麼是時間複雜度？

某個演算法的時間複雜度？

舉例

這個算起來也太麻煩了吧

big-O

例子

big-O

小測驗

小測驗

時間複雜度很重要嗎？

很重要

第一個例題！

作法其一

作法其一 複雜度

這樣OK嗎?

作法其二

作法其二

作法其二

作法其二 複雜度

第一個例題 實作時間

複雜度真的很重要

第二個例題！

第二個例題！ 版本一

第二個例題！ 版本二

版本一 \(Q\leq 100\)，\(N\leq 10^{10}\)

試除法 複雜度

第二個例題 版本一 實做時間

版本二 \(Q\leq 10^6\)，\(N\leq 10^{6}\)

篩法

篩法 複雜度

第二個例題 版本二 實作時間

第二個例題！

有此一說(僅供參考)

有此一說(僅供參考)

怎麼估時間複雜度？

估時間複雜度的方法

第三個例題！

某個作法

某個作法

某個作法

某個作法

某個作法

某個作法

某個作法

某個作法

某個作法

某個作法 分析

某個作法 分析

某個作法 分析

某個作法 分析

某個作法 分析

某個作法 分析

某個作法 分析

某個改進的作法

某個改進的作法 分析

某個改進的作法 分析

第三個例題 實作時間

均攤分析

遞迴函式 複雜度分析

送分題

快速冪

分治預習

準備下課啦

題目小整理

謝謝大家！

APCS Camp時間複雜度

More from Zi-Hong Xiao

講師蕭梓宏

作法其一複雜度

作法其二複雜度

第一個例題實作時間

第二個例題！版本一

第二個例題！版本二

試除法複雜度

第二個例題版本一實做時間

篩法複雜度

第二個例題版本二實作時間

某個作法分析

某個作法分析

某個作法分析

某個作法分析

某個作法分析

某個作法分析

某個作法分析

某個改進的作法分析

某個改進的作法分析

第三個例題實作時間

遞迴函式複雜度分析