圖論
重要名詞
圖論裡的圖(graph):由節點(vertex),邊(edge)組成

無向圖
有向圖
(有箭頭,只能單向走訪)


邊權
走過那個邊的代價(無向有向都可以有邊權)

其他
- 環:一個點經過一些邊可以再回到自己
- 自環:自己連到自己
- 重邊:同樣的邊重複出現
- 一般圖:沒有自環,每有重邊
- 完全圖:有n點,每個n^2個點對都有邊相連
樹
n個點,必有n-1個邊,無環

有向無環圖 DAG(directed acyclic graph)
有向圖,不形成環

入度(in degree):連進一個節點的邊數
出度(out degree):連出一個節點的邊數
如何存圖?
鄰接矩陣
給n個節點,n*n的二維矩陣adj[a][b]=1代表a連到b1代表a連到b,=0代表沒連到
空間複雜度O(n^2)

鄰接陣列
給n個節點,m個邊
開n個空vector,第i個vector代表點i有連到vector裡的點
空間 - O(n+m)

鄰接陣列
code example
#include <iostream>
using namespace std;
const int maxn = 1e5;
vector<int> adj[maxn];
int main()
{
// n nodes, m edges
int n, m;
cin>>n>>m;
for(int i=0;i<m;++i){
// one directional edge from a to b
int a, b;
cin>>a>>b;
adj[a].push_back(b);
}
}
圖的走訪
dfs
depth first search
深度優先搜尋法
用遞迴一直往一條路徑走下去,直到不能走在退回去找其他路走
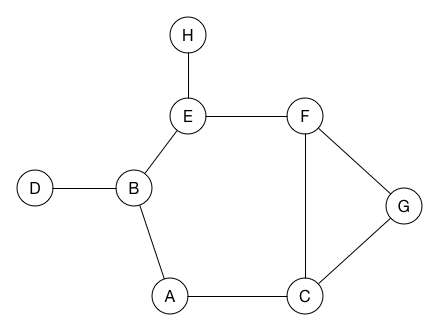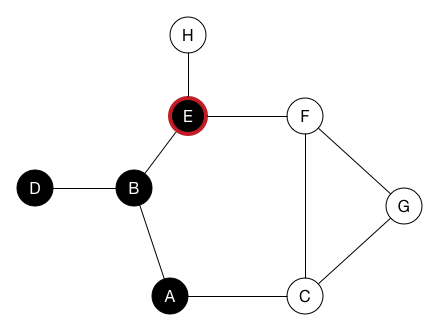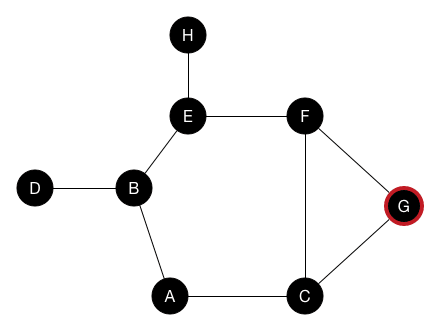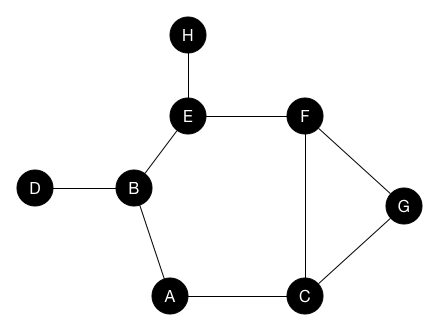
走訪時記一個visit陣列紀錄走過的點
實作
int visit[100000];
vector<int> adj[10000];
void dfs(int v){
visit[v]=1;
for(int i=0;i<adj[v].size();++i){
int a = adj[v][i];
if(!visit[a]) dfs(a);
}
}bfs
breadth first search
廣度優先搜尋法
一層一層走訪
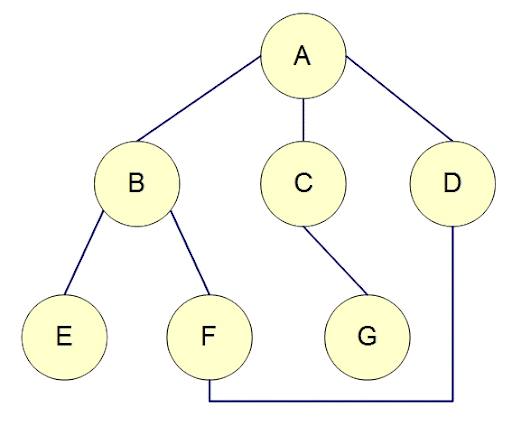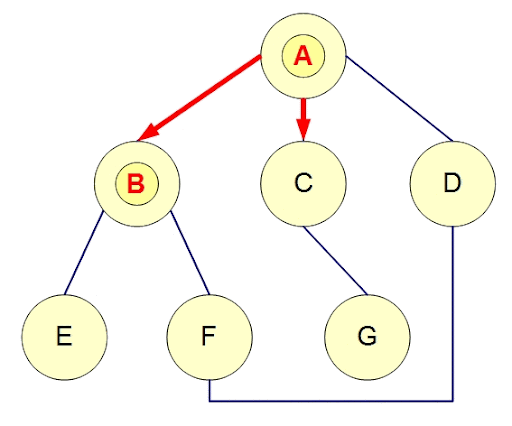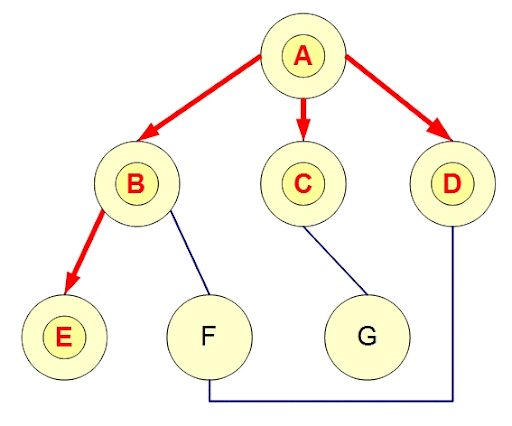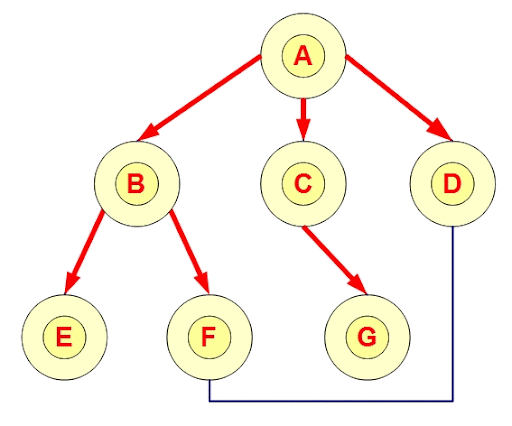
用queue實作,每次走訪queue最前面的點,把其連到的點放進queue的尾端
vector<int> adj[100000];
int visit[100000];
void bfs(int st) {
queue<int> q;
q.push(st);
visit[st] = 1;
while(!q.empty()) {
int v=q.front();
q.pop();
for (auto a:adj[v]) {
if (!visit[a]) {
q.push(a);
visit[a] = 1;
}
}
}
}可以拿來算無邊權最短路徑(dfs不太行)
原因,queue裡越前面的點代表越早連到,所以如果一個點有兩個路徑連到,較短的一定會在queue的前面
其實很多bfs/dfs圖論題兩種都適用
最短路徑
最短路演算法很多種,但實用的只有dijkstra和floyd warshall
有向/無向圖中,帶權的最短路徑
dijkstra's algorithm
單源最短路徑
令:
n個點
s為起點
dis[v]代表s到v的最點距離
weight[a][b]為邊a-b的權重
done[v]=1代表點v已走過(預設0)
-
從沒走過的點中,找一個點x其dis[x]最小的,設done[x]=1,所以一開始x就是起點s
- 用priority_queue找最小的dis[x]
- 對於每個x連到的點y,做dis[y]=min(dis[y],dis[x]+weight[x][y])
- 重複直到都走過
邊權不能是負的
\(O(E \log V)\)
#include <bits/stdc++.h>
#define NL "\n"
using namespace std;
vector<pair<int,int> > gh[100010];
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0);
int n, m, u, v, w;
cin>>n>>m;
for(int i=0;i<m;++i){
cin>>u>>v>>w;
gh[u].push_back({v, w});
gh[v].push_back({u, w});
//doesn't matter if there's multiple line between two nodes, the algorithm will take the least one
}
//init
vector<int> done(n, 0);
vector<int> dis(n, 1e9);
dis[0]=0; //default dis[s] is 0
priority_queue<pair<int,int>, vector<pair<int,int> >, greater<pair<int,int> > > pq;
pq.push({dis[0], 0});
while(!pq.empty()){
pair<int,int> x=pq.top();
pq.pop();
if(done[x.second]) continue;
done[x.second]=1;
for(auto a:gh[x.second]){
if(done[a.first]) continue; //not necessary
if(dis[x.second]+a.second<dis[a.first]){
dis[a.first]=dis[x.second]+a.second;
pq.push({dis[a.first], a.first});
}
}
}
}
floyd warshall
dis[i][j]代表i到j的最短路
做一個類似dp的東西
對於dis[i][j],枚舉i~j的中點k
轉移:dis[i][j]=min(dis[i][j], dis[i][k]+dis[k][j])
可用於權重為負值的情況,但不能有負環
\(O(n^3)\)
for(int k = 1; k <= n; k++){
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
dp[i][j]=min(dp[i][j], dp[i][k]+dp[k][j]);
}
}
}dis預設=鄰接矩陣(沒連到的設無線大)
迴圈的順序要注意
拓樸排序
用拓樸排序把dag壓成一個序列
其序列要滿足每個點一定要往前指
因為dag是有向無環,所以一定存在一個序列使的邊不會往前指
紀錄每個點的入度,把入度為0的拔掉,並把其連出的邊也拔掉(把他們連到的點的入度-1)。
重複直到所有點都被拔完
#include <bits/stdc++.h>
using namespace std;
vector<int> graph[100010];
int main() {
int n, m;// n: 點個數 m:邊個數
cin >> n >> m;
vector<int> cnt(n, 0);
int a, b;
for(int i=0;i<m;++i){
cin >> a >> b;
graph[a].push_back(b);
cnt[b]++;
}
// find the node with no edge
queue<int> topo;
for(int i=0;i<n;++i)
if(cnt[i]==0)
topo.push(i);
vector<int> ans;
while(!topo.empty()){
int v=topo.front();
topo.pop();
ans.push_back(v);
for(int a:graph[v]){
cnt[a]--;
if(cnt[a]==0)
topo.push(a);
}
}
}
拓樸排序可以拿來做dp
dag最短路為例:
從第一個位置開始,比對它所連到位置其路徑長(or加權重)是否為最小
$$dp[j]=min(dp[j], dp[i]+weight[i][j])$$
j為i連到的地方,weight[i]為邊的權重。
最小生成樹
生成樹:在一連通圖中,選擇一些邊,使一張圖連通,而且任兩點路徑唯一
aka 在一張圖中找一棵樹,有n-1個邊
最小生成樹:有權重的圖中,選擇的邊權和最小的生成樹
1
2
3
4
5
9
2
3
5
7
15
6
Kruskal's Algorithm
- 先將所有邊以權重由小排到大
- 開一個並查集
- 從小考慮到大,如果目前的邊兩端點在同一個集合,代表都在生成樹了,反之將之加進生成樹(合併集合)
\(O(m\log m)\)
struct e{
int u, v, w;
};
vector <e> edge;
bool cmp(e a, e b){
return a.w < b.w;
}
int main(){
int n, m;
cin >> n >> m;
for(int i = 0; i < m; i++){
int a, b, w;
cin >> a >> b >> w;
edge.push_back({a, b, w});
}
sort(edge.begin(), edge.end(), cmp);
int sum = 0;
for(int i = 0; i < m; i++){
int u = edge[i].u, v = edge[i].v, w = edge[i].w;
if(findroot(u) != findroot(v)){
connect(u, v);
sum += w;
}
}
}Prim's Algorithm
和Dijkstra類似
改成每次尋找離目前最小生成樹最近的點
用priority_queue維護連出去最小的邊
#define f first
#define s second
typedef pair <int, int> pii;
bool visit[100005];
vector <pii> g[100005];
priority_queue <pii, vector <pii>, greater <pii> > pq;
int prim(){
int sum = 0;
pq.push({0, 1});
while(!pq.empty()){
pii tmp = pq.top();
pq.pop();
if(visit[tmp.s]) continue;
visit[tmp.s] = true;
sum += tmp.f;
for(auto i : g[tmp.s]){
pq.push({i.s, i.f});
}
}
return sum;
}例題
LCA
lowest common ancestor
最低共同祖先
有一棵樹,兩個節點的lca即為兩節點往上走第一個相遇的點
有一棵樹,兩個節點的lca即為兩節點往上走第一個相遇的點
最低共同祖先
用途:找出樹上兩點的路徑
法一 - 倍增法
倍增表:紀錄每個點往上\(2^0, 2^1, 2^2, 2^3...\)層會到的節點
anc[v][i]代表點v往上\(2^i\)個點的祖先
ex:樹上第k祖先
先跳到第16個祖先,停在第16個祖先後再往上跳2個,再跳1個
觀察k=19的二進位組成:\(19_{(10)}=10011_{(2)}\),所以\(19=2^4+2^1+2^0\)
如何找lca?

chennn種的樹
如何找lca?

chennn種的樹
1. 把深度較深的點移到跟另一個點一樣的深度
如何找lca?

chennn種的樹
2. 從大的長度開始跳,如果跳上去\(anc[a][i]!=anc[b][i]\)
,就跳上去
如何找lca?

chennn種的樹
跳\(2^1\)
如何找lca?

chennn種的樹
最後lca會在兩點的往上一個
// par==上面的anc
ll n, q, par[200010][21];
vector<int> adj[200010];
int level[200010]; //深度
void dfs(int v){
for(auto a:adj[v]){
par[a][0]=v;
level[a]=level[v]+1;
dfs(a);
}
}
ll lca(int a, int b){
if(level[a]<level[b]) swap(a, b);
//set a and b to the same level
int d=level[a]-level[b];
rep(i,0,21) if(d & (1<<i)) a=par[a][i];
if(a==b) return a;
for(int i=20;i>=0;--i){
if(par[a][i]!=par[b][i]){
a=par[a][i];
b=par[b][i];
}
}
return par[a][0];
}
void solve(){
cin>>n>>q;
ll v;
rep(i,2,n+1){
cin>>v;
adj[v].pb(i);
}
par[1][0]=1;
level[1]=1;
dfs(1);
for(int j=1;j<=20;++j){
for(int i=1;i<=n;++i){
par[i][j]=par[par[i][j-1]][j-1];
}
}
int a, b;
while(q--){
cin>>a>>b;
cout<<lca(a, b)<<NL;
}
}
留給你們自學
圖論
By alan lai
圖論
- 457



