
第一章 运动的描述

高中物理——绪论课

什么是物理学?
物理学研究的是物质的最普遍的运动形式和物质的基本结构,它是其他自然科学的基础。

为什么要学物理?
三、物理学改变了世界
第一次突破:牛顿力学的建立和热力学的发展。导致了蒸汽机的发明,使人类进入了蒸汽动力时代,引发了第一次工业革命。
瓦特的改良蒸汽机
斯蒂芬逊的蒸汽机车


三、物理学改变了世界
第二次突破:19世纪,法拉第发现了电磁感应现象,麦克斯韦创立了电磁理论,推动了电机、电器、电信设备等的发明和制造,使人类进入了电气时代。


法拉第在给公众做科普讲座
马可尼和他的无线电器械
三、物理学改变了世界
第三次突破:20世纪以来,根据相对论、量子力学,大力开发新材料、新光源、新能源,发展了微电子技术、计算机技术,使人类进入了信息时代。


秦山核电站
互联网
四、高中物理与初中物理的区别
高中物理的知识面更广,内容更丰富,更深入
初中物理较多的是定性的描述,高中物理则有较多的定量计算。
初中物理以现象为主,比较直观,高中物理则要透过现象看本质,有一定的抽象思维要求。



物理核心素养
辩证唯物主义世界观
世界是物质的,物质是运动的,
运动是有规律的,规律是可以认识的,
认识是发展变化的。

第一章 运动的描述
你可据此推测出哪些关于车辆运动的信息?
在本章中我们将:
1.认识和理解位移、速度、加速度等物理量。
2.经历质点模型的建构过程,初步学会测量物体的瞬时速度。
3.学习用文字、关系式、图像描述简单的实际运动。


第一节
质点 物理模型

第一节
质点 物理模型
一、机械运动


鸟儿飞翔
滑板运动
物体空间位置随时间的变化

第一节
质点 物理模型


鸟儿飞翔
滑板运动

鸟、人等具有一定大小和形状的研究对象上各部分的运动情况不尽相同

第一节
质点 物理模型
二、质点
在某些情况下,可以忽略物体的大小和形状,把实际物体抽象为一个有质量的点。


第一节
质点 物理模型

何种条件下可将物体抽象为质点?
当研究对象的尺寸与其运动范围相比小得多时

月球可以看成质点吗?


第一节
质点 物理模型
例1:列车沿直线轨道通过隧道。两位同学对列车是否能视为质点持有不同观点,他们的观点在一定的条件下都是合理的。讨论什么情况下列车可以视为质点,什么情况下列车不能视为质点。


第一节
质点 物理模型

何种条件下可将物体抽象为质点?
某些情况下,关注的是研究对象整体的运动,无需考虑对象各部分的运动差异

大雁可以看成质点吗?

第一节
质点 物理模型
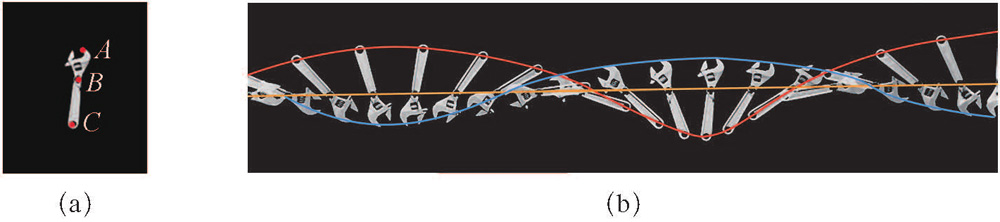
例2:当将扳手放在光滑水平面上推出后,会发现扳手边旋转边向前运动,如果不考虑扳手的旋转,可以认为扳手整体在做匀速直线运动。如图(a)所示,在扳手的三个位置标注A、B、C三点。图(b)是扳手由左向右运动的部分频闪照片,图中画出了扳手上A、B、C三点在水平面上运动的轨迹,试问扳手上哪个点的运动可以反映扳手整体的运动。说明理由。


第一节
质点 物理模型
为何要构建物理模型?


建立模型是关键。……模型就是通过我们对问题现象的了解,利用我们考究得来的机理,吸收一切主要因素、略去一切次要因素所制造出来的“一幅图画“。
——钱学森

第一节
质点 物理模型
把复杂问题简单化,再把简单问题模型化,可以更好地研究事物,抓住问题的本质,发现规律。
科学研究中的其他模型
为何要构建物理模型?

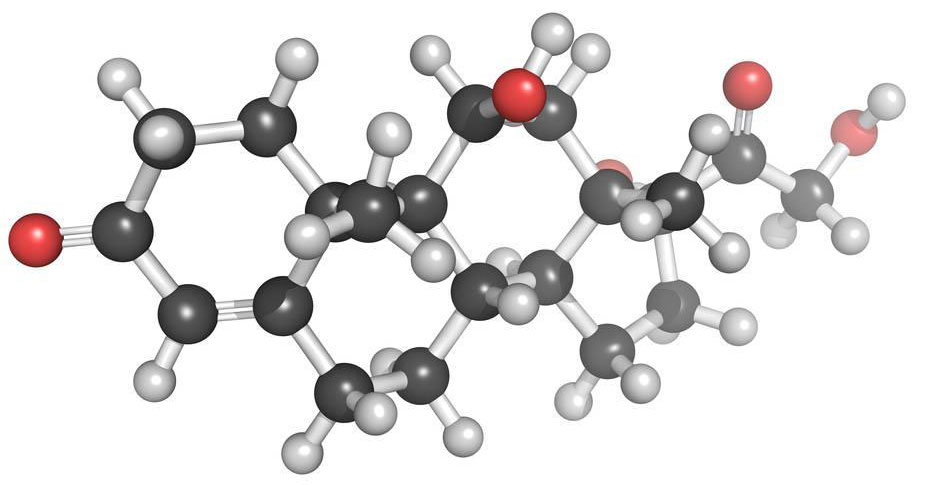
化学键模型
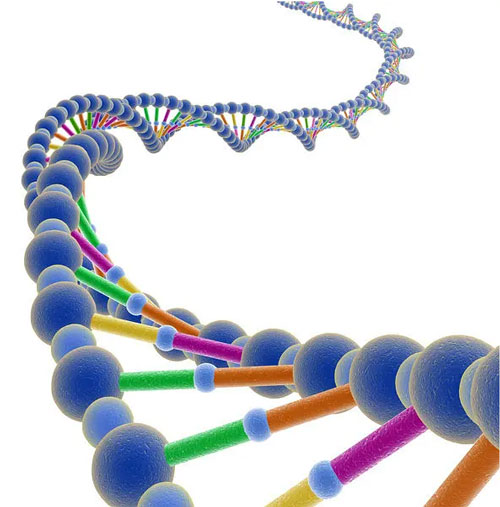
双螺旋结构模型
气象模型


第一节
质点 物理模型
一、机械运动
物体空间位置随时间的变化
二、质点(物理模型)
在某些情况下,可以忽略物体的大小和形状,把实际物体抽象为一个有质量的点。
条件:取决于研究的问题
次要因素
主要因素

第二节
位置的变化 位移


第二节
位置的变化 位移
一、时间与时刻
市八中学作息时间表
| 节次 | 时间 |
|---|---|
| 1 | 8:00-8:40 |
| 2 | 8:50-9:55 |
| 3 | 10:30-11:10 |
| 4 | 11:20-12:00 |
| 午休 | |
| 5 | 13:00-13:40 |
| 6 | 13:50-14:30 |
| 8 | 14:45-15:25 |
| 9 | 15:35-16:15 |
列车时刻表


第二节
位置的变化 位移
一、时间与时刻
在下列各项叙述中,表示时间的是( )
(A)奥运会上,苏炳添用9.83 s跑完了100 m
(B)中央电视台新闻联播节目从19时开始
(C)1997年7月1日零时我国政府开始对香港恢复行使主权
(D)由于火车提速,从上海到北京又缩短2小时

第二节
位置的变化 位移

一、时间与时刻
时间轴:时刻 \(t\) 为一点,时间(间隔)\( \Delta t\) 为一段
2
1
3
4
5
6
/s
请在时间轴上标出:前 3 s、第 5 s,第 4 s 末,第 5 s 初。

第二节
位置的变化 位移

参考系
二、路程与位移
通常以地球为参考系,用直角坐标系的坐标来表示物体的位置
甲
乙

如图所示,新中国成立70周年阅兵仪式上,国产武装直升机排列并保持“70”字样编队从天安门上空飞过。甲、乙分别是编队中的两架直升机,则( )
(A)以甲为参考系,乙是运动的
(B)以乙为参考系,甲是运动的
(C)以甲为参考系,坐在观众席上的观众都是静止的
(D)以乙为参考系,编队中所有直升机都是静止的

第二节
位置的变化 位移

如何描述物体位置的变化?
二、路程与位移

路程:物体在运动过程中通过的路径(或轨迹)长度
标量与矢量
位移:物体位置的变化
表示:有向线段
方向:起点指向终点
大小:起点到终点的直线距离

第二节
位置的变化 位移


二、路程与位移
请在图上用有向线段表示 A 到 B、 B 到 C 的位移,并给出该同学在整个过程中的位移大小。

第二节
位置的变化 位移
二、路程与位移
什么情况下路程等于位移
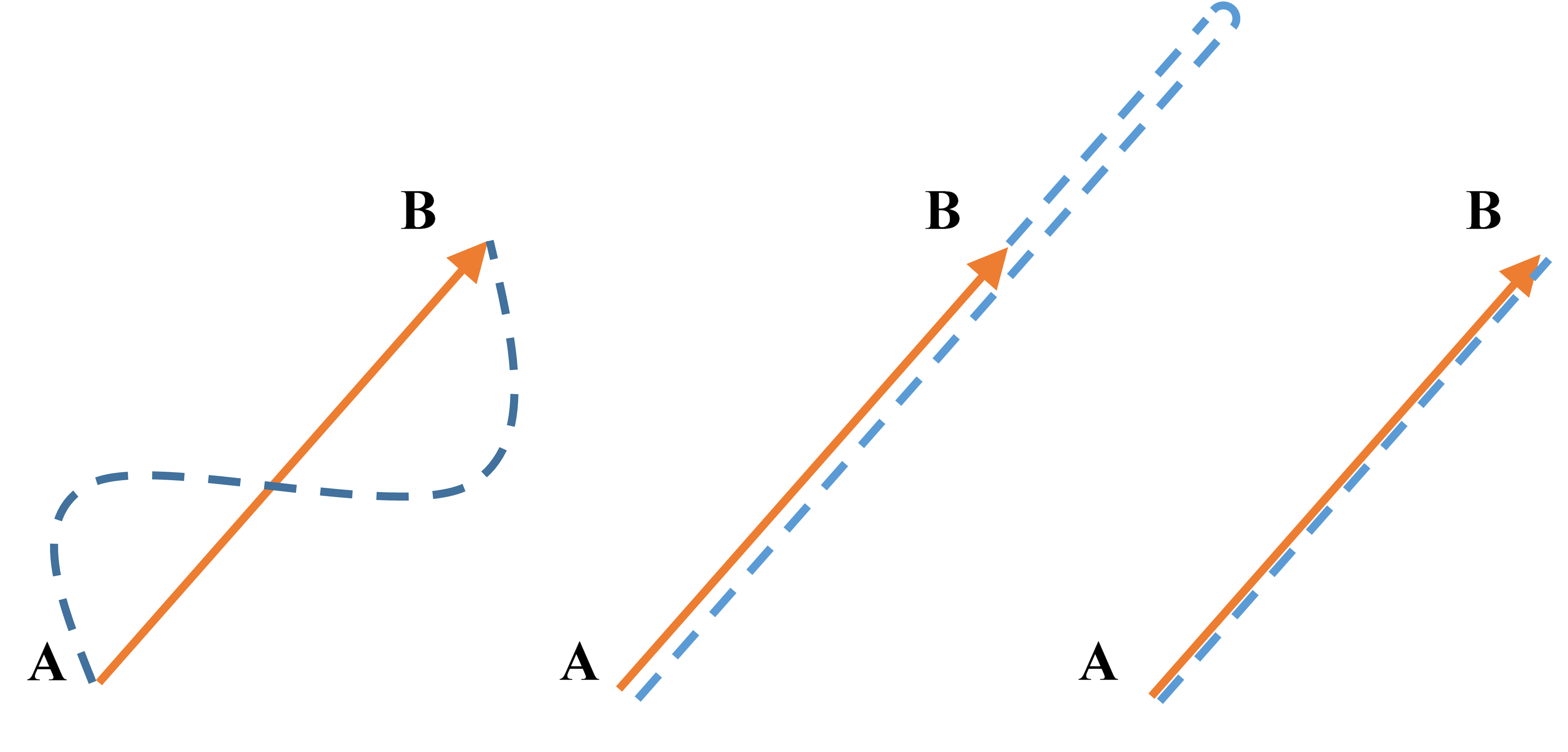
的大小?
概念辨析

第二节
位置的变化 位移
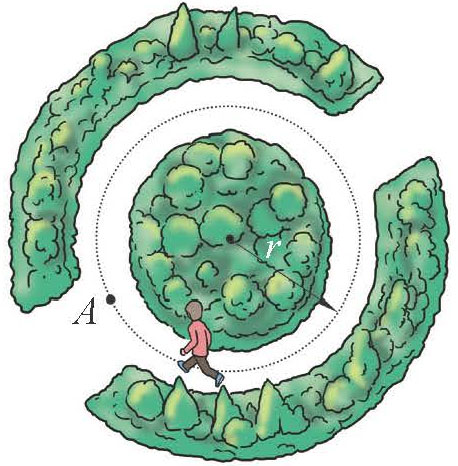
例2 如图所示的圆形大花坛的环形道路半径为 r,某人从 A 点出发沿环形道路健身跑。当他的位移大小刚好等于环形道路的直径时,他经过的路程是多少?


第二节
位置的变化 位移
一、时间与时刻
二、路程与位移
路程:物体在运动过程中通过的路径(或轨迹)长度
标量与矢量
位移:物体位置的变化
表示:有向线段
方向:起点指向终点
大小:起点到终点的直线距离
时间轴

第二节
位置的变化 位移

如何描述做直线运动物体的位移?

二、路程与位移
位置
(一点)
位移
(一段)

第二节
位置的变化 位移

例3 足球运动员进行折返跑训练。运动员先沿着 x 轴正向跑动,经 A 点到达 B 点后转身,沿 x 轴负向跑到 C 点。各点的位置如图所示。试据此填写表。

| A点坐标 | B点坐标 | C点坐标 | 从A到B的位移 | 从B到C的位移 | 从A到C的位移 |
|---|---|---|---|---|---|

第二节
位置的变化 位移

如何描述做直线运动物体的位移?

小球沿水平方向运动的频闪照片

用 \(x-t\) 图像表示
表述物理规律的三种常用方法
文字叙述
图像
数学关系

第二节
位置的变化 位移

例4 一跑步者在不同时刻的位置数据如表所示,利用表中的数据作图。在 5.5 s时,跑步者位于何处?如果跑步者继续按此规律运动,何时距离出发点 35 m?
| 时刻 t/s | 位置 x/m |
|---|---|
| 0.0 | 0.0 |
| 1.0 | 4.9 |
| 2.0 | 10.0 |
| 3.0 | 15.1 |
| 4.0 | 19.9 |
| 5.0 | 25.0 |
| 6.0 | 30.1 |


第二节
位置的变化 位移

例5 如图所示为 A 、 B 两人运动的 \(x-t\) 图像。 A 保持匀速运动直达终点, B 晚出发一段时间。图中哪根图线表示 A 的运动? A 、 B 两人谁先到达终点?


第二节
位置的变化 位移

如何测量做直线运动物体位移的大小?

皮尺

超声波测距仪

第二节
位置的变化 位移
传感器




位移传感器
电压传感器
电流传感器
力传感器

光电门传感器
数据采集器

计算机

三、数字化信息系统(DIS)
数据采集
处理
显示

第二节
位置的变化 位移
三、数字化信息系统(DIS)
传感器




位移传感器
电压传感器
电流传感器
力传感器

光电门传感器
数据采集


处理
显示
物理信息
电信号
数字信息
数值、图像
数据采集器
注意:此页未完成,参见空中课堂的处理

第二节
位置的变化 位移
位移传感器

位移传感器(接收器)
位移传感器(发射器)

红外线
超声波


第三节
位置的变化的快慢 速度

为什么照片中的运动员出现了“拖影”?
如何判断运动员的移动快慢?

第三节
位置的变化的快慢 速度
一、速度

匀速直线运动:任意相等时间内物体的位移总是相等的运动(理想模型)
描述物体运动的快慢(位置变化的快慢)和方向
速度是矢量,方向为位移的方向
单位:m/s
速度:位移与发生这段位移所需的时间的比

第三节
位置的变化的快慢 速度
一、速度
\( x-t \) 图像
\( v-t \) 图像
斜率 \(k = \frac{\Delta x}{\Delta t} \) 表示速度


第三节
位置的变化的快慢 速度
二、平均速度
变速直线运动:相等时间间隔内物体的位移不总是相等的运动
平均速度:位移与发生这段位移所需的时间的比
平均速度是矢量,方向为位移的方向
粗略描述物体运动的快慢和方向

第三节
位置的变化的快慢 速度
二、平均速度


第三节
位置的变化的快慢 速度
三、瞬时速度
瞬时速度:某时刻或某位置的速度
瞬时速度是矢量,方向为物体运动方向
精确描述物体运动的快慢和方向

第三节
位置的变化的快慢 速度

例1 下列关于各种“速度”的说法中,哪些是平均速度?哪些是瞬时速度?
(1)羽毛球比赛中的最高球速曾达到 420 km/h
(2)高铁经 12 min 加速到 350 km/h
(3)台风中心以 20 km/h 的速度向西北方向移动
(4)车辆通过 1 km拥堵路段耗时 20 min,车速仅为 3 km/h

第三节
位置的变化的快慢 速度

例2 如图所示是设立在学校附近的限速标志牌,在这段道路上全程限速 30 km/h。一辆汽车通过该路段 150 m 的距离所用的时间为18 s 。请判断此车是否超速,并作出分析。


第三节
位置的变化的快慢 速度
一、速度
匀速直线运动:任意相等时间内物体的位移总是相等的运动(理想模型)
描述物体运动的快慢(位置变化的快慢)和方向
速度是矢量,方向为位移的方向
单位:m/s
速度:位移与发生这段位移所需的时间的比
二、平均速度
变速直线运动:相等时间间隔内物体的位移不总是相等的运动
平均速度:位移与发生这段位移所需的时间的比
平均速度是矢量,方向为位移的方向
粗略描述物体运动的快慢和方向
三、瞬时速度
瞬时速度:某时刻或某位置的速度
瞬时速度是矢量,方向为物体运动方向
精确描述物体运动的快慢和方向

第三节
位置的变化的快慢 速度

平均速度与瞬时速度的方向
物体在某段时间内沿如图所示轨迹从A运动到B。则:
(1)初始时刻(位置)A的瞬时速度 \( v_A \) 的方向为向 ;
(2)末时刻(位置)B的瞬时速度 \( v_B \) 的方向为向 ;
(3)全过程平均速度 \( \bar {v}\) 的方向为向 。

第三节
位置的变化的快慢 速度
大飞机C919在试飞时曾以 800 km/h 的速度沿着直航线匀速巡航 15 min。
(1)根据这些信息能否确定飞机在15 min内的位移?
(2)800 km/h是飞机的平均速度还是瞬时速度?

匀速直线运动是瞬时速度保持不变,瞬时速度与平均速度相等的运动

第三节
位置的变化的快慢 速度




斜率 \(k = \frac{\Delta x}{\Delta t} \) 表示速度 \(v\)
请说出下列 \(x-t\) 图像中 2 s 末 的瞬时速度

第三节
位置的变化的快慢 速度
一物体运动的 \( x-t \) 图像如图所示,则下列说法正确的是( ) 。
(A)0.5 s时物体的速度为 6 m/s
(B)第3 s末物体的速度为 \( \frac{8}{3} \) m/s
(C)第3 s内物体的平均速度为 2 m/s
(D)4 s内物体的平均速度为 2.5 m/s
在图像中读取多段运动的平均速度、瞬时速度

第三节
位置的变化的快慢 速度
一质点沿直线做单向的运动,若前一半时间的平均速度为 \(4 \rm{m/s}\) ,后一半时间的平均速度为 \(6 \rm{m/s}\) ,求:
(1)整个过程的平均速度的大小;
(2)若其他条件不变,若质点前一半位移的平均速度为 \(4 \rm{m/s}\) ,后一半时间的平均速度为 \(6 \rm{m/s}\) ,则整个过程的平均速度多大?
多段运动的平均速度

第三节
位置的变化的快慢 速度
某人爬山,从山脚爬上山顶,然后又从原路返回到山脚,上山的平均速率为 \( v_1 \),下山的平均速率为 \(v_2\),求:
(1)往返全过程的平均速度;
(2)往返全过程的平均速率。
平均速度和平均速率

第三节
位置的变化的快慢 速度
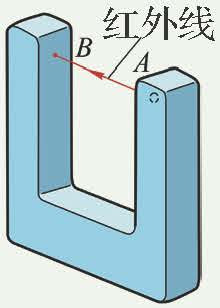
用光电门测量物体的瞬时速度
实验原理:某时刻(或某位置)附近极短时间(或极短位移)内的平均速度可视为物体在该时刻的瞬时速度
光电门传感器

测量的是挡光时间\(\Delta t\)
若再给出挡光片的宽度\(\Delta x\)
则可以计算出速度\(v=\frac{\Delta x}{\Delta t}\)

第三节
位置的变化的快慢 速度
用光电门测量物体的瞬时速度

实验装置
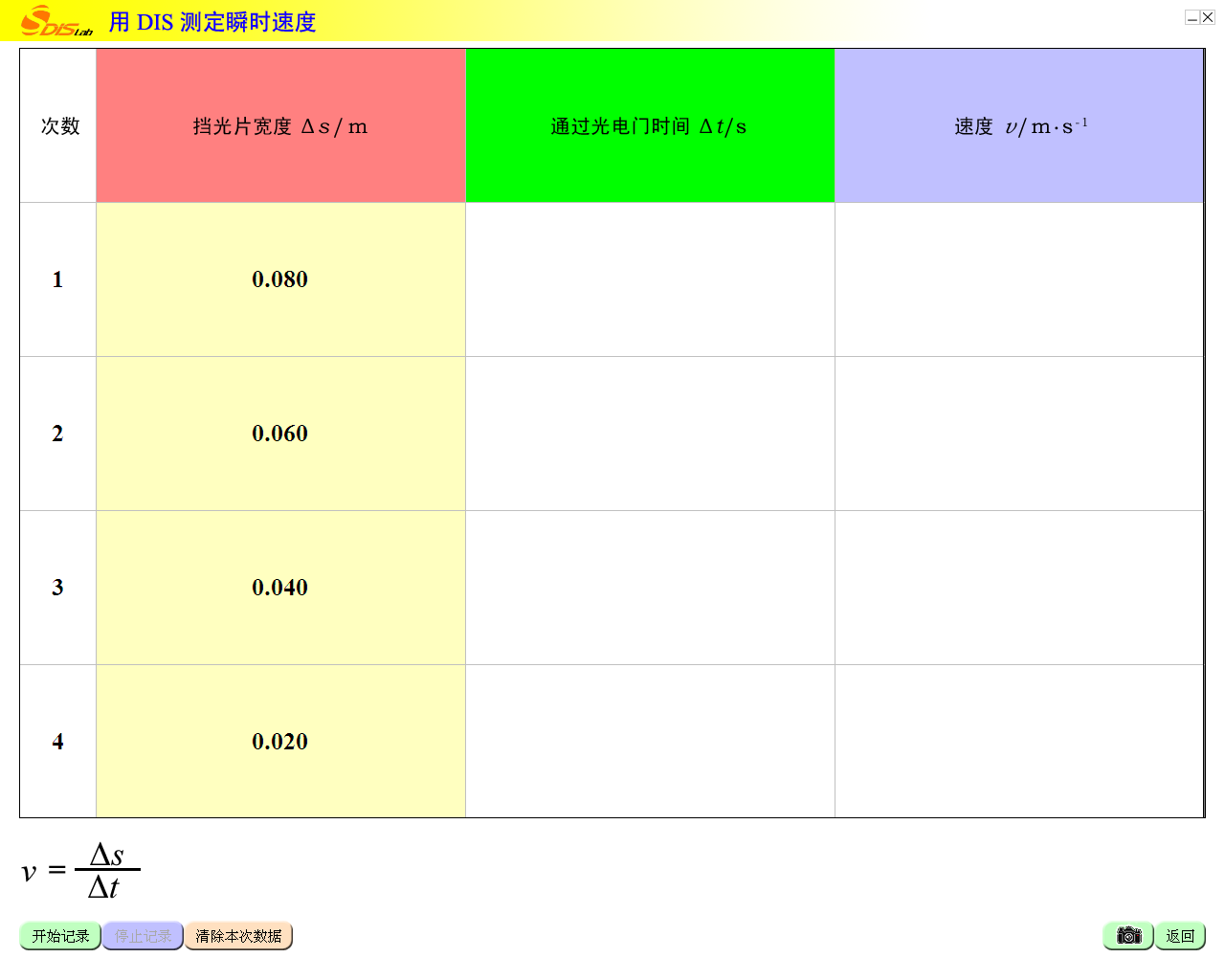
不同宽度挡光片做4次

第四节
速度变化的快慢 加速度

起跑时有的运动员冲到了前面,或者说速度增加得比其他运动员快

第四节
速度变化的快慢 加速度
怎样描述物体速度变化的快慢
(1)哪个物体的速度变化量最大?哪个物体的速度变化量最小?
(2)哪个物体的速度变化最快?哪个物体的速度变化最慢?
飞机以 200 m/s 的速度沿直线匀速飞行


运载火箭点火后升空,2 s 内由 0 m/s 加速到 60 m/s
赛车沿直线赛道启动,从静止加速到 100 km/h 约需 2.5 s


第四节
速度变化的快慢 加速度

第四节
速度变化的快慢 加速度
一、加速度(acceleration)
描述物体运动的快慢(位置变化的快慢)和方向
速度是矢量,方向为位移的方向
单位:\(\rm{m/s}\) 或 \(\rm{m·s^{-1}}\)
速度:位移与发生这段位移所用时间的比
描述速度变化的快慢和方向
单位:\(\rm{m/s^2}\) 或 \(\rm{m·s^{-2}}\)
速度变化量与发生这一变化所用时间的比

第四节
速度变化的快慢 加速度
一、加速度(acceleration)
描述速度变化的快慢和方向
单位:\(\rm{m/s^2}\) 或 \(\rm{m·s^{-2}}\)
速度变化量与发生这一变化所用时间的比
加速度是速度随时间的变化率

某个量 \(D\) 的变化量可记为 \(\Delta D\),如果发生这个变化所用的时间为 \(\Delta t\),则 \(\Delta D\) 与 \(\Delta t\) 的比 \( \frac{\Delta D}{\Delta t} \) 称为 \(D\) 的变化率。速度是位置的变化率,加速度是速度的变化率。变化率表示变化的快慢。

第四节
速度变化的快慢 加速度

A、B 两车均做直线运动。A 车的速度从 0 增大到 30 km/h,B 车从 20 km/h加速到 60 km/h,两辆车的速度分别变化了多少?哪辆车的加速度更大?
1
一、加速度(acceleration)

第四节
速度变化的快慢 加速度
一、加速度(acceleration)
某同学骑自行车从静止开始运动,经 10 s 后速度增大到 5 m/s,在这段时间内自行车的速度变化量为_______m/s,平均加速度为_______\(\rm{m/s^2}\);以 5 m/s 的速度到达路口附近后,自行车减速 2 s 即停止,在这段时间内,自行车的速度变化量为________m/s,平均加速度为_________\(\rm{m/s^2}\)。
练习册P12/7

第四节
速度变化的快慢 加速度
一、加速度(acceleration)

与速度有平均速度、瞬时速度之分类似,加速度也有平均加速度和瞬时加速度。
一般而言,物体做变速运动时速度变化的快慢程度也会随时间和空间位置而变化。此时,速度的变化量 \(\Delta v\) 与所用时间 \(\Delta t\) 的比即为该段时间内的平均加速度。平均加速度只能粗略地表示某段时间内物体速度变化的快慢程度。
如果 \(\Delta t\) 无限趋近于0,即得到某一时刻速度的瞬时变化率,相应的加速度称为瞬时加速度。瞬时加速度描述了物体在某时刻、经过相应位置速度变化的快慢。

第四节
速度变化的快慢 加速度
一、加速度(acceleration)
刚开始点火升空时,火箭的加速度可达14 \(\rm{m/s^2}\),所以火箭的速度在 1 s 时间内增加了 14 m/s。这一说法正确吗?为什么?
练习册P12/5

第四节
速度变化的快慢 加速度
一、加速度(acceleration)
- 速度大,加速度也大
- 加速度大,速度变化量也大
- 加速度大小不变,速度大小也一定不变
概念辨析
练习册P13/8

第四节
速度变化的快慢 加速度
二、加速度的方向
某同学骑自行车从静止开始运动,经 10 s 后速度增大到 5 m/s,在这段时间内自行车的速度变化量为__ 5___m/s,平均加速度为___0.5____\(\rm{m/s^2}\);以 5 m/s 的速度到达路口附近后,自行车减速 2 s 即停止,在这段时间内,自行车的速度变化量为___-5___m/s,平均加速度为___-2.5___\(\rm{m/s^2}\)。
练习册P12/7
问:负号代表的物理意义是什么?

第四节
速度变化的快慢 加速度
二、加速度的方向
根据加速度的定义:\(a = \frac{\Delta v}{\Delta t} \),加速度 \(a\) 的方向与速度变化量 \(\Delta v\) 的方向一致
即速度变化的方向

第四节
速度变化的快慢 加速度
二、加速度的方向
一辆沿直线行驶的汽车在 5 s 内速度由 15 m/s 增加到 25 m/s,在随后的 5 s 内速度减小到 15 m/s。如图所示,取汽车前进方向为正方向,分别画出两段时间内的初速度与末速度矢量。
用速度、加速度矢量表示下述两个过程
结论:加速时 \(a\)、\(v\) 同向;减速时 \(a\)、\(v\) 反向
书本P20

第四节
速度变化的快慢 加速度
二、加速度的方向
概念辨析
练习册P13/8
- 加速度增大,速度也随之增大
- 加速度的大小减小时,速度的大小可能增大

第四节
速度变化的快慢 加速度
二、加速度的方向

如图所示,一个弹性小球在光滑水平面上以 5 m/s 的速度撞墙后,以大小不变的速度反向弹回。球与墙的接触时间为 0.1 s。用速度矢量表示撞墙前、后小球速度 \(v\) 和速度变化量 \(\Delta v\),并求小球在与墙接触过程中的加速度 \(a\)。
4


第四节
速度变化的快慢 加速度
二、加速度的方向

某小车运动的 \(v-t\) 图像如图所示。\(t_1\) ~ \(t_2\)、 \(t_3\) ~ \(t_4\) 时间间隔内的 \(v-t\) 图像近似看作直线。这两段时间内,小车的加速度为多大?设小车运动方向为正方向,\(t_1\)~ \(t_2\) 时间内的加速度和 \(t_3\) ~ \(t_4\) 时间内的加速度是正还是负?说明理由。
6


第四节
速度变化的快慢 加速度
二、加速度的方向
9
练习册P12/7
如图(a)、(b)所示分别为质点做直线运动的 \(x-t\) 图像和 \(v-t\) 图像,其中OBC和OBʹCʹ分别表示质点1和质点2的运动,DE和DʹEʹ分别表示质点3和质点4的运动。仿照下表第一行,将表格填写完整。

第四节
速度变化的快慢 加速度
二、加速度的方向
一、加速度(acceleration)
描述速度变化的快慢和方向
单位:\(\rm{m/s^2}\) 或 \(\rm{m·s^{-2}}\)
速度变化量与发生这一变化所用时间的比
即速度变化的方向
加速时 \(a\)、\(v\) 同向;减速时 \(a\)、\(v\) 反向

第一章 运动的描述
实验
测量做直线运动物体的瞬时速度
三
用分体式位移传感器测量加速度
二
用分体式位移传感器测量位移
一
1、练习使用DIS
2、用DIS测位移和平均速度


1、练习使用DIS
一
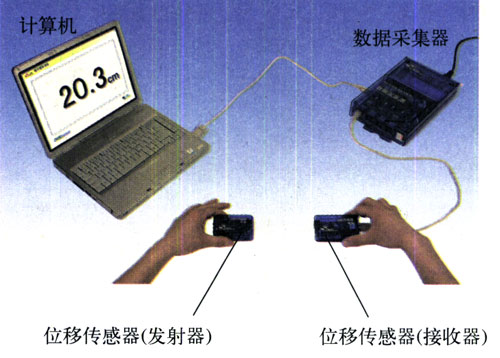
将位移传感器的发射器与接收器正对放置,开启发射器电源,
观察计算机界面上的数据变化

2、测量位移和平均速度
一

位移传感器发射器
位移传感器接收器
数据采集器
导轨,调成倾斜
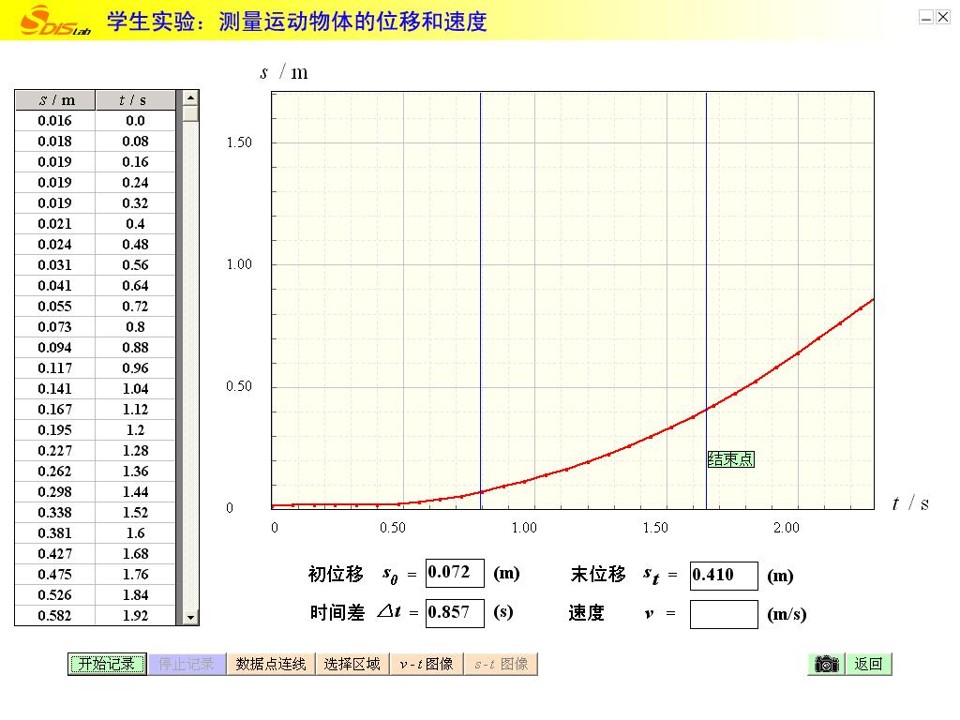
“选择区域“(例如1.00~1.50 秒)
得出该时间内的平均速度

测量加速度
二


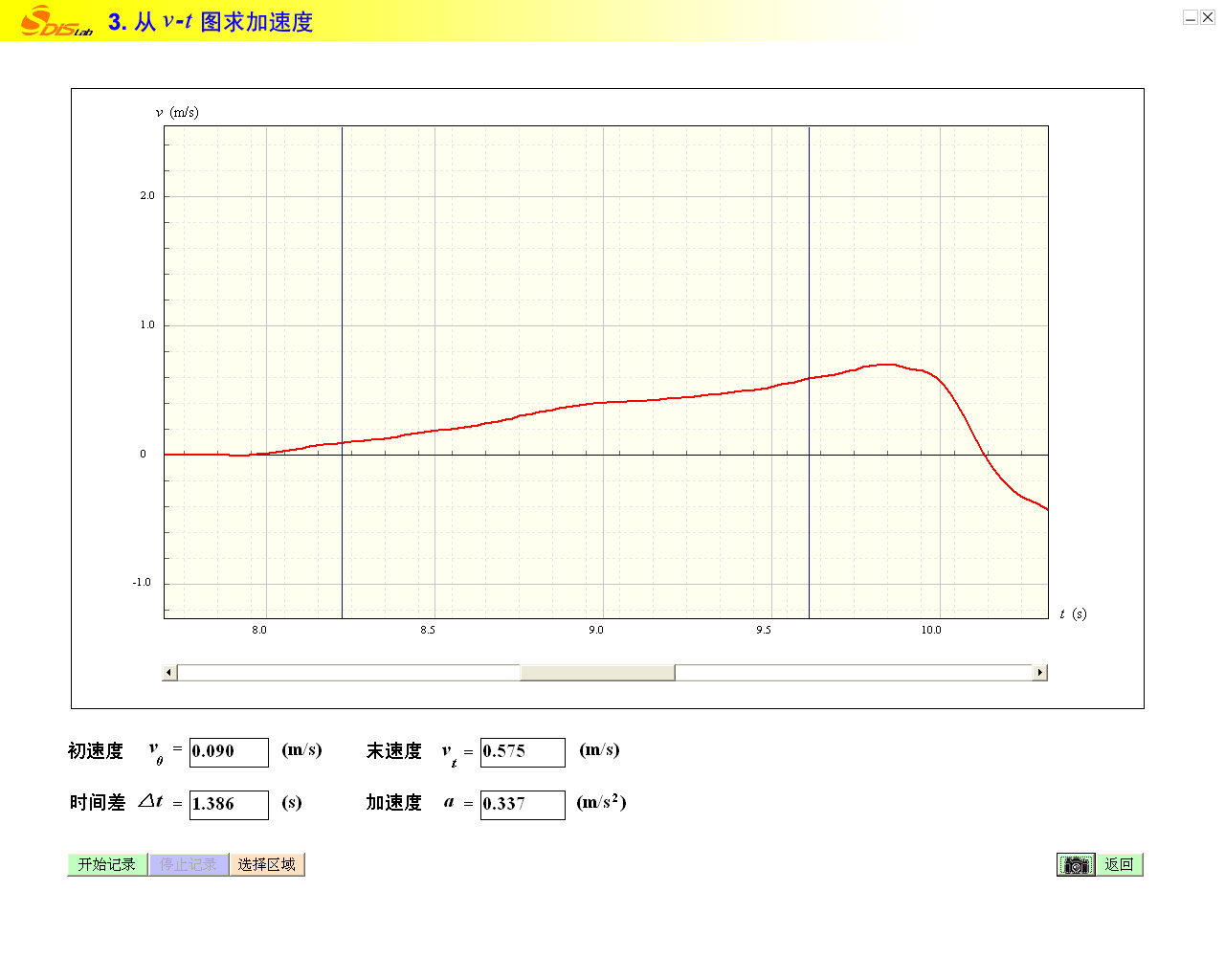
“选择区域“
得出该时间内的平均加速度
测量瞬时速度
三

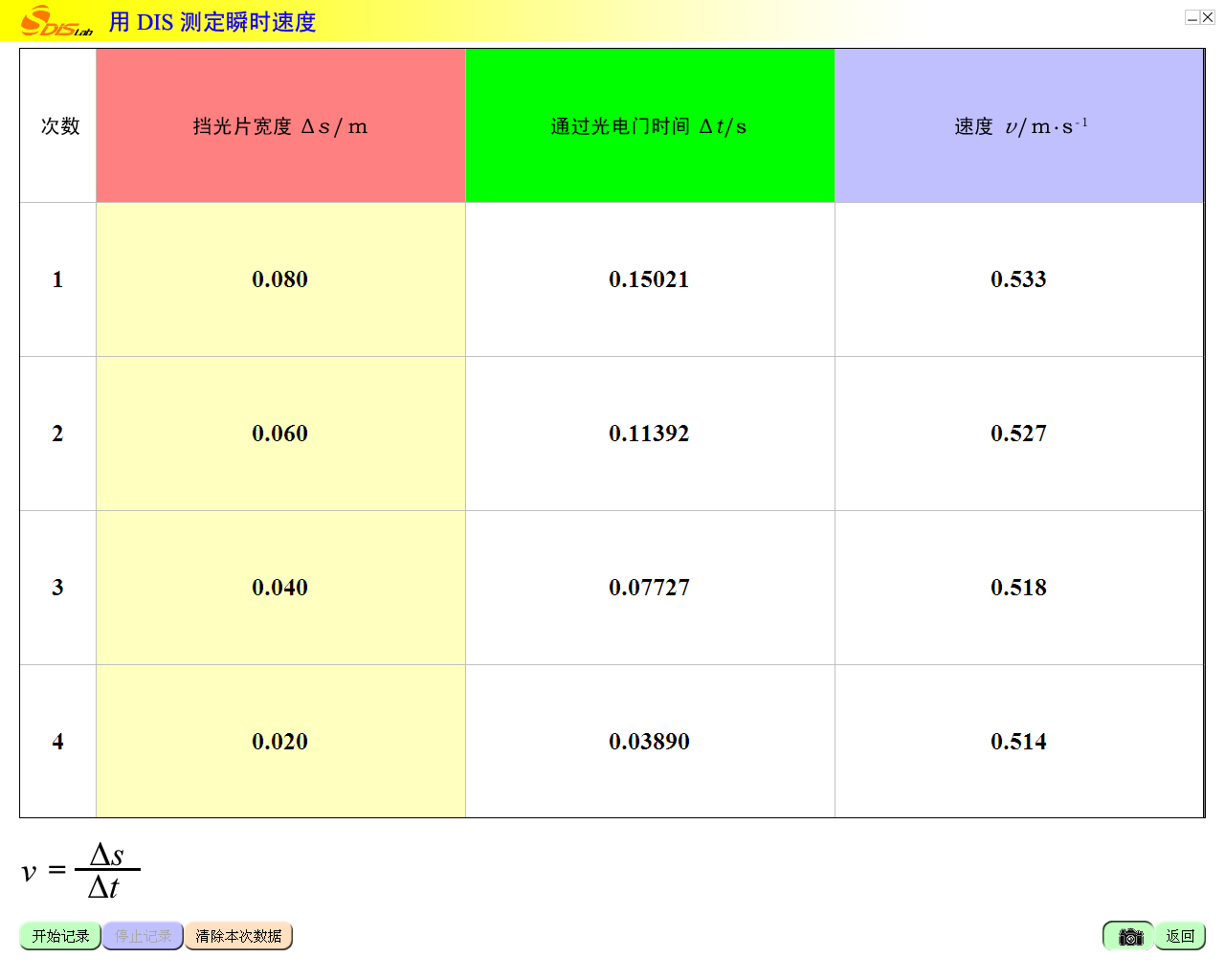
依次将8cm、6cm、4cm、2cm宽度的挡光片放置在小车上
注意:每次都需从同一位置由静止释放小车
将支架移至轨道中部
将接收器换成光电门
将发射器从小车上拆除
换成挡光片

通用软件的使用
补
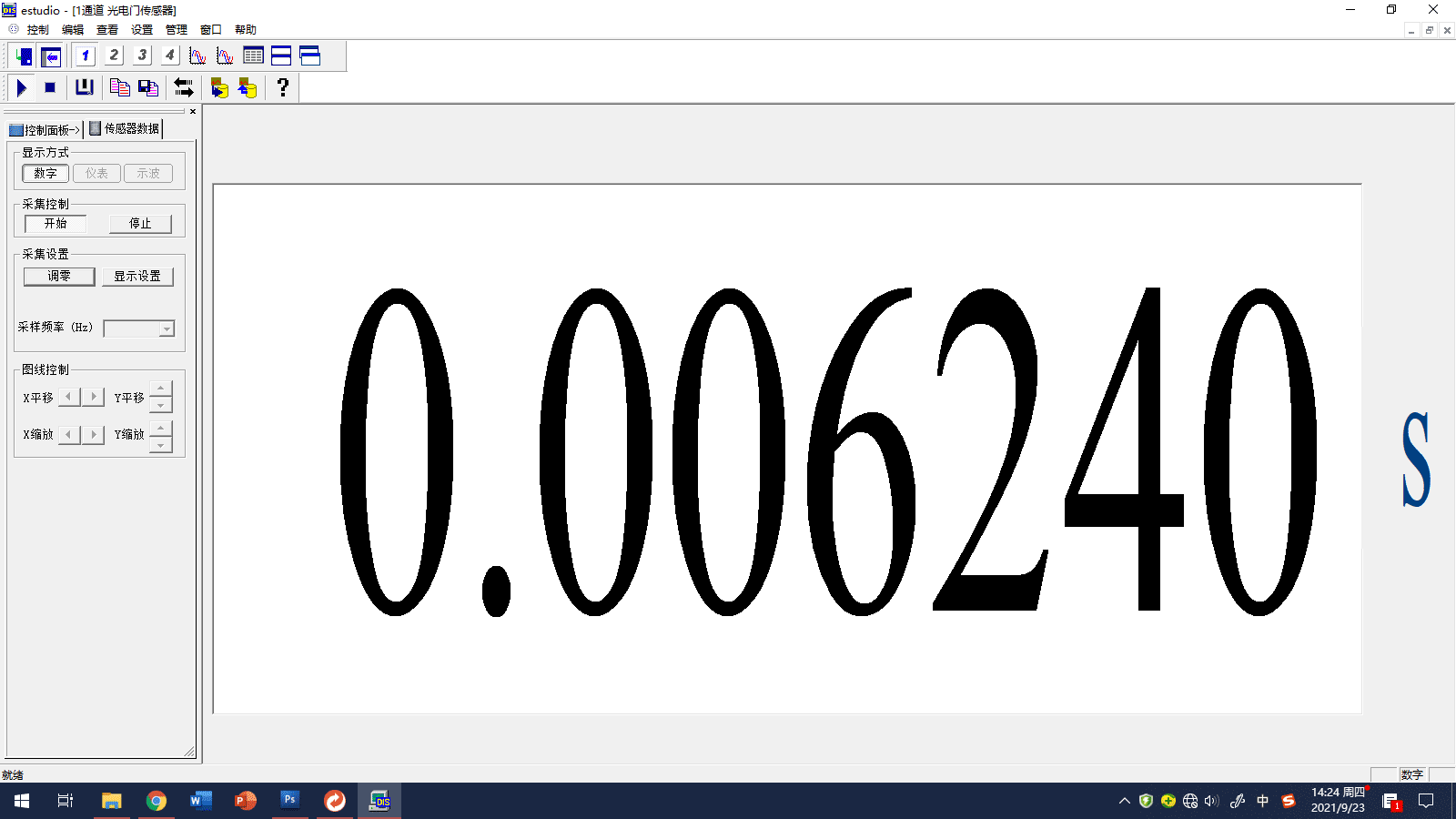
光电门的通用软件界面,测量的是挡光时间

位移传感器的通用软件界面——数字形式

位移传感器的通用软件界面——图像形式
位移传感器的通用软件界面——图像形式
请通过操作,使界面上出现如下图所示的 \(x-t\)图像

第一章 运动的描述
By fjphysics
第一章 运动的描述
- 796



