第五章 机械能
锥体“上滚”
第五章A 功
功（Work）的要素
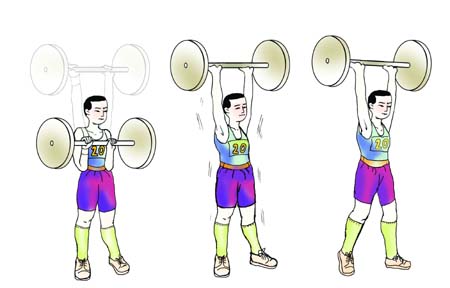
1
力、物体在力方向上的位移
F
上举过程
挺住不动
匀速向前移动
F
F
s
s
功的计算
2
W=Fs \cos \theta
W=Fs \cos \theta
功的计算
2
力对物体所做的功W等于力的大小F、位移的大小s、力和位移之间夹角θ的余弦三者的乘积。
F
s
θ
功的计算
2
1、首先确定研究对象。
2、对物体进行受力分析，作出物体的受力图。
3、找准每个力与位移方向之间的夹角θ。
4、根据功的公式：W＝Fscosθ求解。
计算力对物体做功的步骤
功的计算
2
1 用此公式计算功时，α为力和位移方向上的夹角，F必须为恒力。
2 做功与物体运动形式无关，也就是说，力对物体做功具有独立性。
3 计算功时，一定要明确是计算哪个力对物体所做的功，不能张冠李戴。
力对物体做功的理解
当\( \theta= \frac{\pi}{2} \)时，\( \cos \theta=0 \)，\( W=0\)，这时力的方向与位移的方向垂直，力不做功。
当\(\frac{\pi}{2}＜\theta≤ \pi \)时，\( \cos \theta＜0 \)，\( W＜0\)，这时力做的功为负值，或者说物体克服力做功。
当\( 0≤\theta＜\frac{\pi}{2} \)时，\( \cos \theta＞0 \)，\( W＞0\)，这时力做的功为正值。
正功和负功
3
注意：虽然功有正负，但功是标量，符号并不表示方向。
如图所示，一位老爷爷在一片平坦的草地遛狗，拉狗的绳子与地面夹角为30°，设绳的拉力始终是20 N，在向前运动2 m的过程中拉力做了多少功 ？
正功和负功
3
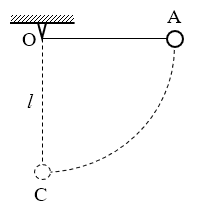
如图所示，用一根长 l＝0.8 m的细绳拴住一个质量为0.5 kg的小球悬挂在O点，将小球拉至A点使细绳呈水平状态。求从释放小球到细绳和小球摆至竖直位置OC的过程中，重力和细绳的拉力对小球做的功。（g取10 m/s 2）
正功和负功
3
Title Text
合力做功的求法
先把合力F求出来，然后用公式W=Fscosθ计算合力所做的功。
先把每个分力所做的功算出来，然后求它们的代数和，即合力所做的功等于每个分力所做功的代数和。
正功和负功
3
在F-s图中，表示F与s关系的曲线和坐标轴所包围的面积表示功的大小。
功的图示
4
s
F
W
第五章B 功率
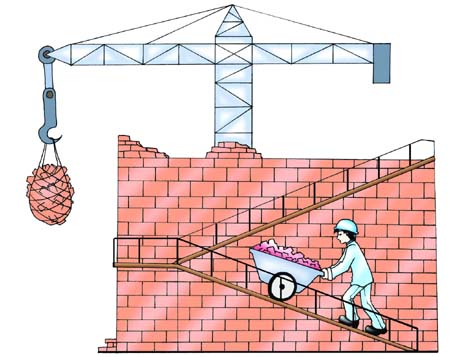
做功的快慢
1、做功是否相同？
2、做功快慢是否相同？
在建筑工地，将砖块送到楼顶
功率的定义
1
P= \frac {W}{t}
功 W 跟完成这些功所用时间 t 的比值，叫做功率。
单位是W（读作瓦），1 W = 1 J/s
功率的计算
2
P= \frac {W}{t}
定义式：
P= Fv
推论：
推导过程：\(P=\frac{W}{t} =\frac{Fs}{t}=Fv\)
平均功率和瞬时功率
3
\overline{P}= \frac {W}{t}
平均功率
P= Fv
瞬时功率
\overline{P}= F\overline{v}
额定功率和实际功率
4
额定功率：机械正常条件下长时间工作的最大功率
实际功率：机械实际运行时的功率
第五章C 动能
E_{k}=\frac{1}{2}mv^2
第五章D 重力势能
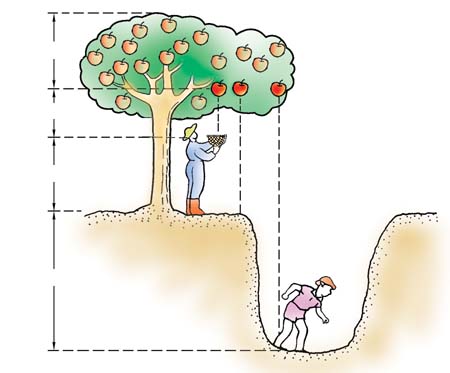
3、重力做功的特点
重力做功与路径无关，仅取决于始点与终点的位置
第五章E 功和能量变化的关系
第五章F 机械能守恒定律
八年级第二学期物理课本
1、动能和势能的相互转化
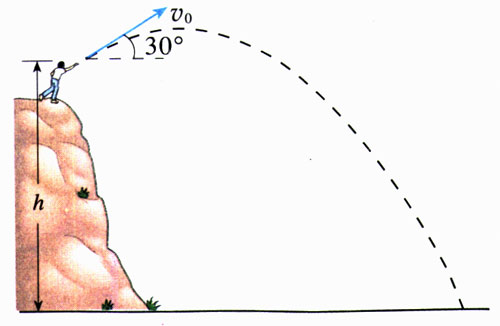
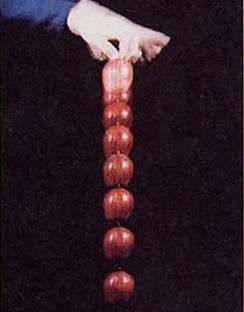
自由落体运动
抛体运动
动能和重力势能之间的相互转化
过山车
1、动能和势能的相互转化
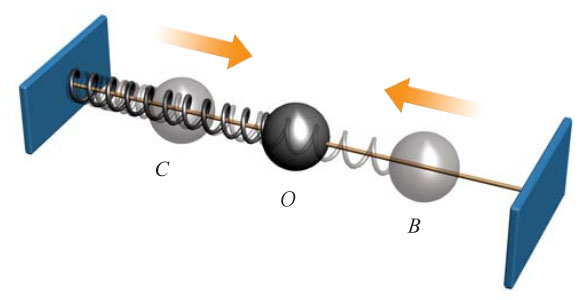
动能和弹性势能之间的相互转化
动能、重力势能和弹性势能
之间的相互转化
弹簧振子
撑杆跳
2、机械能
动能、势能统称为机械能
E=E_k+E_p
提桶碰鼻
3、机械能守恒定律
守恒条件
只有重力做功
表达式
mgh_1+\frac{1}{2}mv_1^2=mgh_2+\frac{1}{2}mv_2^2
3、机械能守恒定律
如何理解只有重力做功？
物体只受重力
除重力外还受其他力，但其他力不做功
自由落体运动
抛体运动
接触面光滑
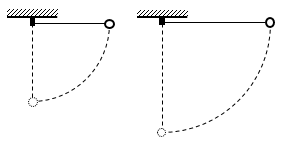
不计空气阻力
3、机械能守恒定律
判断下面各个实例中，哪些是机械能守恒？为什么？说明理由。
（1）跳伞运动员带着张开的降落伞在空气中匀速下降。
（2）不计空气阻力，把手榴弹或标枪斜向上抛出。
（3）用细绳拴着一个小球，绳的一端固定，使小球在光滑水平面上做匀速圆周运动。
（4）用细绳拴着一个小球，绳的一端固定，设法使小球在竖直平面上做匀速圆周运动。
（5）物体沿着光滑的曲面滑下，如图（a）所示。
（6）拉着一个物体沿着光滑的斜面匀速上升，如图（b）所示。
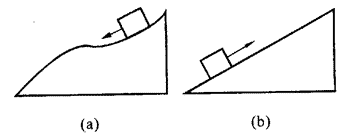
3、机械能守恒定律
一小球做自由落体运动，求下落45m高度时速度为多大？（ g 取 10 \(m/s^2\)）
3、机械能守恒定律
质量为 0.5 kg 的石块从 10 m 高处以 30° 角斜向上方抛出，速度 \(v_0\) 的大小为 5 m/s。求：（不计空气阻力， g 取 10 \(m/s^2\)）
（2）求落地时的速度大小。
结论： \({W_F}= \Delta {E_k}\) 如何运用？（做正功的情况）
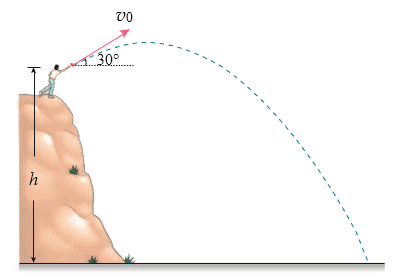
机械能守恒定律： \({mgh_1}+\frac{1}{2}mv_1^2= {mgh_2}+\frac{1}{2}mv_2^2\)
4、机械能和其他形式能的转化
情景：跳伞运动员带着张开的降落伞匀速下落
机械能转化为什么能？
（3）
机械能增加还是减少？
（2）
除重力之外还有什么力做功，做正功还是负功？
（1）
4、机械能和其他形式能的转化
情景：拉着一个物体在光滑斜面匀速上升
什么能转化为机械能？
（3）
F
机械能增加还是减少？
（2）
除重力之外还有什么力做功，做正功还是负功？
（1）
功是能量转化的量度
W 合正功， E k增加； W 合负功， E k减少
1
W G正功， E p减少； W G负功， E p增加。 W G=-ΔEp
2
W 除G外正功， E增加； W 除G外负功， E减少
3
DIS实验：验证机械能守恒定律
观察由同一高度释放的摆锤上升的最大高度
1
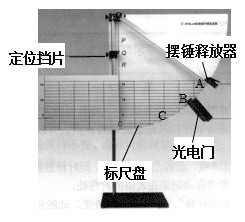
摆锤释放器
定位挡片
DIS实验：验证机械能守恒定律
验证机械能守恒定律
2
摆锤释放器
光电门传感器
\begin{aligned} mgh_{\rm A}+\frac{1}{2}mv{\rm_A}^2=mgh_{\rm B}+\frac{1}{2}mv{\rm_B}^2 \\
=mgh_{\rm C}+\frac{1}{2}mv{\rm_C}^2=mgh_{\rm D}+\frac{1}{2}mv{\rm_D}^2 \end{aligned}
要验证
h_A=0.15\,{\rm{m}},h_B=0.10\,{\rm{m}},h_C=0.05\,{\rm{m}},h_D=0.00\,{\rm {m}}
已知
v_A=0.0\,{\rm{m/s}}
（每次都从A点静止释放）
只需测
v_B，v_C，v_D
DIS实验：验证机械能守恒定律
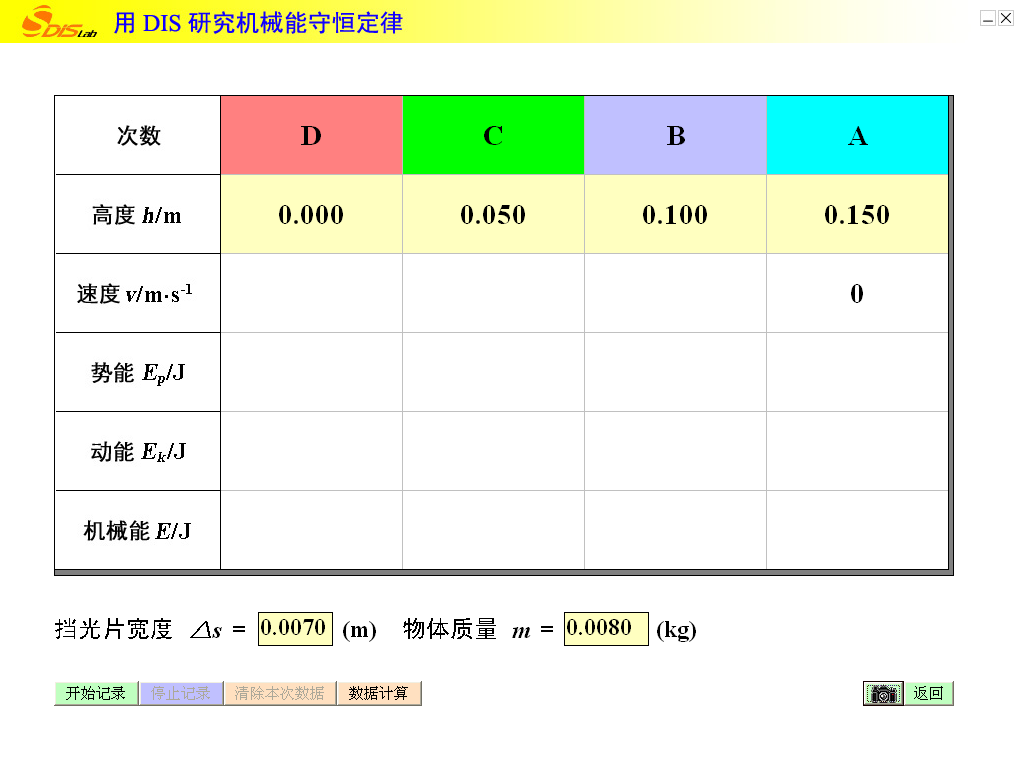
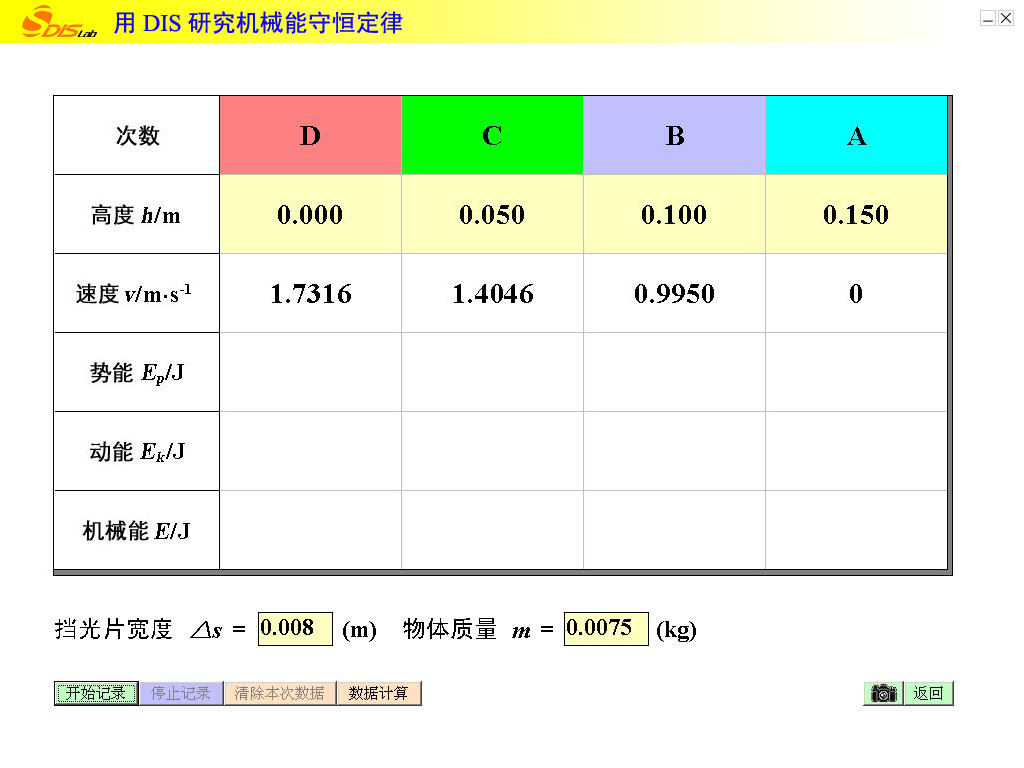
(1）实验1中，装上定位挡片，将摆锤从A点静止释放，观察到它到达左侧最高点，此点与A点高度基本相同。由此得到的结论是：摆锤②。（选填“①”或“②”）
①在摆动过程中，机械能处处相等
②在左侧最高点的机械能与A点的机械能基本相等
在如图所示的“用DIS研究机械能守恒定律”的实验中，有实验1和实验2两部分。
1
（2）请按正确的实验2顺序填写下列步骤：__________。
①开启电源，运行DIS应用软件，点击实验条目中的“研究机械能守恒定律”软件界面
②卸下“定位挡片”和“小标尺盘”，安装光电门传感器并接入数据采集器
③摆锤置于A点，点击“开始记录”，同时释放摆锤，摆锤通过D点的速度将自动记录在表格的对应处
④把光电门传感器放在大标尺盘最底端的D点，并以此作为零势能点。A、B、C点相对于D点的高度已事先输入，作为计算机的默认值
⑤点击“数据计算”，计算D点的势能、动能和机械能
⑥依次将光电门传感器放在标尺盘的C、B点，重复实验，得到相应的数据
1
在如图所示的“用DIS研究机械能守恒定律”的实验中，有实验1和实验2两部分。
②①④③⑤⑥
（3）（多选题）除了以上实验步骤，该实验还需要测量的物理量有（ BC ）
A．摆线的长度 B．摆锤的直径
C．摆锤的质量 D．摆锤下落的时间
1
在如图所示的“用DIS研究机械能守恒定律”的实验中，有实验1和实验2两部分。
2
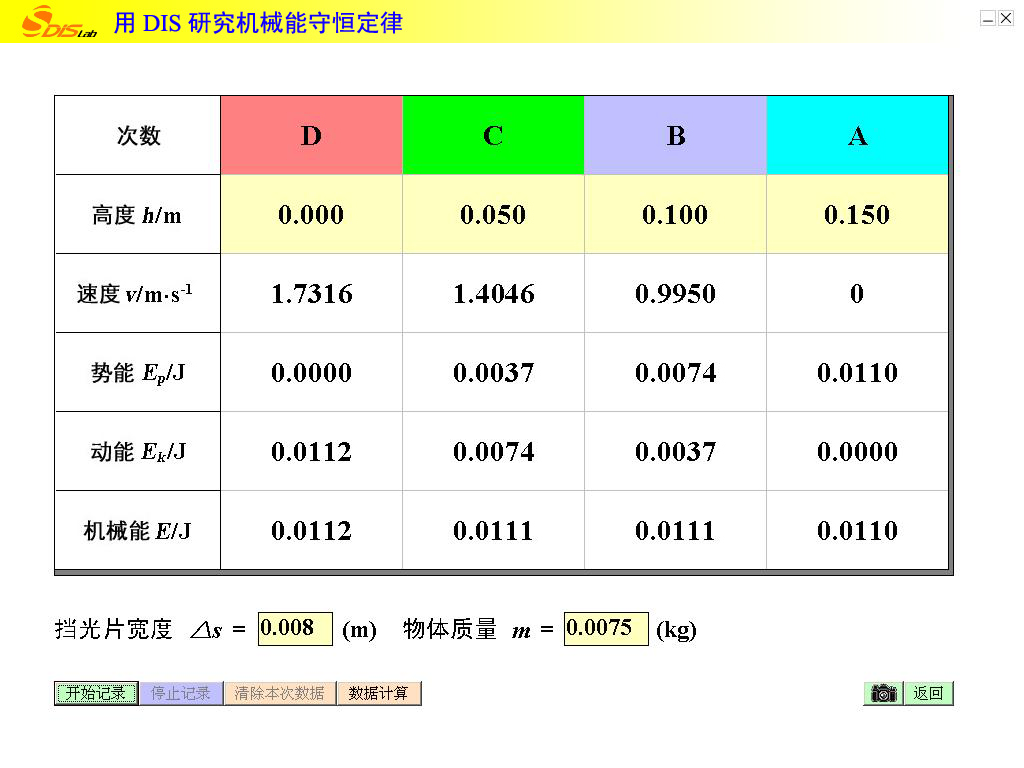
“用DIS研究机械能守恒定律”的实验中，用光电门测定摆锤在某一位置的瞬时速度，从而求得摆锤在该位置的动能，同时输入摆锤的高度（实验中A、B、C、D四点高度为0.150m、0.100m、0.050m、0.000m，已由计算机默认），求得摆锤在该位置的重力势能，进而研究势能与动能转化时的规律。
（1）实验时，把___D_____点作为了零势能点。
（2）本实验中，先选取零势能面再进行实验，则零势能面位置的选取对验证摆锤动能与重力势能之和为常数__无____影响（选填“有”或“无”）。
2
“用DIS研究机械能守恒定律”的实验中，用光电门测定摆锤在某一位置的瞬时速度，从而求得摆锤在该位置的动能，同时输入摆锤的高度（实验中A、B、C、D四点高度为0.150m、0.100m、0.050m、0.000m，已由计算机默认），求得摆锤在该位置的重力势能，进而研究势能与动能转化时的规律。
（3）（单选）将摆锤由A点静止释放，在摆锤摆到最低点的过程中（ B ）
（A）摆锤只受重力作用
（B）绳子拉力不做功，重力做正功
（C）绳子拉力做负功，重力做正功
（D）摆锤受到的合外力不为零，合外力做功为零
（4）（单选）若实验测得D点的机械能明显偏大，造成该误差的原因可能是（ C ）
（A）摆锤在运动中受到空气阻力的影响 （B）光电门没有放在D点
（C）摆锤在A点不是由静止释放的 （D）摆锤释放的位置在AB之间
3
如图为“DIS研究机械能守恒定律”的实验装置。
（1）请指出该同学实验中的错误之处：
①光电门传感器未放在标尺盘最低端的D点；
②摆锤释放器未置于A点。
（2）图中计算机记录的数据与真实值相比将偏小（填“偏大”、“偏小”或“仍准确”）
4
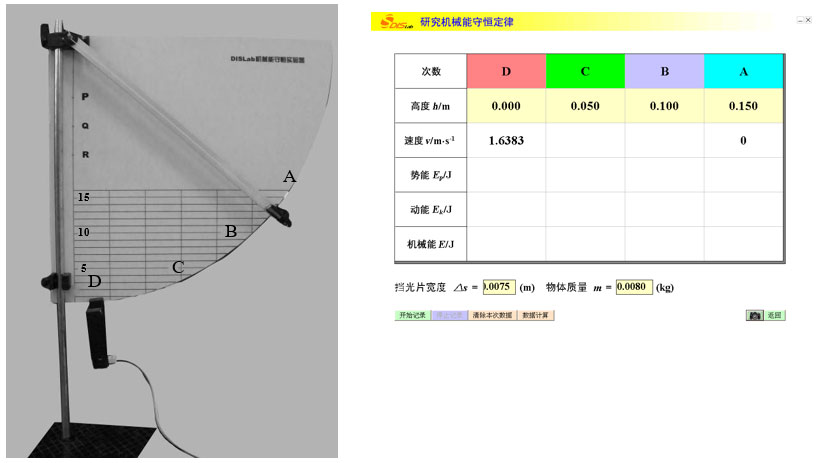
如图所示是在“用DIS实验系统研究机械能守恒定律”的实验装置，完成下列有关问题：
（1）图中摆锤释放器的作用是使摆锤每次从同一位置由静止释放。
（2）每次都准确从同一位置静止释放摆锤，改变传感器安装的高度，以同一零势能面测得四个不同位置的重力势能和动能数据。
|
动能（×10-2J） |
重力势能（×10-2 J） |
机械能（×10-2 J） |
|
0.00 |
7.50 |
7.50 |
|
2.46 |
5.00 |
7.46 |
|
4.91 |
2.50 |
7.41 |
|
7.34 |
0.00 |
7.34 |
分析实验数据可以发现，动能与势能之和（机械能）随测量位置的不同而不断减小，其可能的原因是：摆动过程中存在阻力做负功。
5
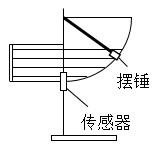
如图为“用DIS研究机械能守恒定律”的实验中，将一传感器先后分别固定在竖直板上的D、C和B三点，最低点D作为零势能点。逐次将摆锤从A点自由释放，分别测出摆锤经过D、C和B点时的速度。
（1）实验中使用的传感器是光电门传感器。
（2）已知摆锤的直径为Δs，由传感器测出摆锤通过传感器时的挡光时间为Δt，则摆锤经过传感器时的速度大小为\(\frac {\Delta s}{\Delta t}\)。
（3）若摆锤直径的测量值大于其真实值会造成摆锤动能的测量值偏大。（选填：“大”或“小”）。
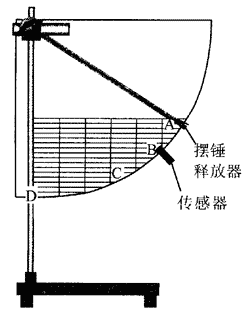
5
如图为“用DIS研究机械能守恒定律”的实验中，将一传感器先后分别固定在竖直板上的D、C和B三点，最低点D作为零势能点。逐次将摆锤从A点自由释放，分别测出摆锤经过D、C和B点时的速度。
（4）已知B、C两点与最低点D和高度差分别为hB、hC，实验测得摆锤经过B、C两点时的速度分别为vB、vC，重力加速度为g。为了证明摆锤在B、C两点的机械能相等，需要得到的关系式是\(\frac{1}{2}v_B^2+gh_B=\frac{1}{2}v_C^2+gh_C\)。
（5）某同学由于操作不当，测得摆锤在B点的机械能明显比在A、C和D的机械能大，其原因可能是___________。
光电门传感器固定在B点下方；摆锤释放点高于A点；摆锤离开A点时速度不为零。
P104/15 在20 m高的平台上，弹簧手枪将质量为10 g的子弹以15 m/s的速度水平射出。若不计空气阻力，子弹落地速度大小为25m/s，弹簧手枪对子弹做的功是1.125 J 。
P100/14 某人在距地面10 m高处以10 m/s的速度抛出一个质量为1.5 kg的物体，不计空气阻力，则此人对物体做的功为75J，物体落地时的速度为\( 10 \sqrt{3} \)m/s 。
=10m
=10m/s
\(v_t = 10 \sqrt{3}\)m/s
\(v_0\)=10m/s
\(v_t\)=25m/s
第五章 机械能
By fjphysics
