An intrinsic geometry for alternating minimization
Flavien Léger
joint work with Pierre-Cyril Aubin-Frankowski
1. Alternating minimization
2. The Kim–McCann geometry
3. Applications
Outline
\begin{aligned}
y_{n+1} &= \argmin_{y\in Y} \phi(x_n,y)\\
x_{n+1} &= \argmin_{x\in X} \phi(x,y_{n+1})
\end{aligned}
For each \(x\in X\): \(y\mapsto \phi(x,y)\) has a unique minimizer.
For each \(y\in Y\): \(x\mapsto \phi(x,y)\) has a unique minimizer.
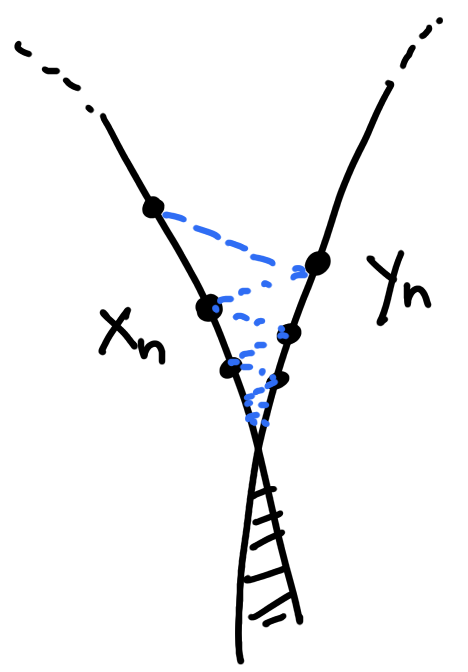
Alternating minimization
\[\operatorname*{minimize}_{x\in X,\,y\in Y} \;\phi(x,y)\]
A L G O R I T H M
\(X,Y\) two sets,
\(\phi\colon X\times Y\to\mathbb{R}\)
Assumptions:
Convergence rates: typically Euclidean space, \(\phi\) convex and \(L\)-smooth
(Beck–Tetruashvili ’13, Beck ’15)
Motivations
Expectation–Maximization in statistics
Sinkhorn (aka RAS, IPFP) for matrix scaling and optimal transport
Projection Onto Convex Sets
\min_{\theta,\pi}\operatorname{KL}(\pi|p_\theta)=:\Phi(\theta,\pi)
\pi\in\Pi(\mu,*),
\theta\in\Theta
model \(p_\theta\)
\(X,Y\): two convex subsets of \(\mathbb{R}^d\)
\min_{x\in X,\,y\in Y}\lVert x-y\rVert^2
Motivations 2: “Gradient descent” family
\[F(x)=\inf_{y\in Y} \phi(x,y)\]
\(X,Y\) two smooth manifolds
x_{n+1} = \displaystyle\argmin_{x\in X} \phi(x,y_{n+1}) \quad\longrightarrow \quad \nabla_x\phi(x_{n+1},y_{n+1})=0
y_{n+1} = \displaystyle\argmin_{y\in Y} \phi(x_n,y) \quad\longrightarrow\quad \nabla_x\phi(x_n,y_{n+1})=\nabla F(x_n)
\phi(x,y)=\frac{1}{2\tau}\lVert x-y\rVert^2 + h(y)\quad\rightsquigarrow\qquad x_{n+1}-x_n=-\tau\nabla F(x_n), \qquad y_n=x_n
\phi(x,y)=\underbrace{u(x|y)} + h(y)\quad\rightsquigarrow\qquad \nabla u(x_{n+1})-\nabla u(x_n)=-\nabla F(x_n), \qquad y_n=x_n
= u(x)-u(y)-\langle\nabla u(y),x-y\rangle
\phi(x,y)=u(y|x) + h(y)\quad\rightsquigarrow\qquad x_{n+1}-x_n=-\nabla^2 u(x_n)^{-1}\nabla F(x_n), \qquad y_n=x_n
\phi(x,y)=\frac{1}{2\tau}d_M^2(x,y)+h(y)\quad\rightsquigarrow\qquad x_{n+1}=\exp_{x_n}(-\tau\nabla F(x_n)), \qquad y_n=x_n
Let \(\lambda\geq 0\). \(\phi\) has the \(\lambda\)-strong FPP if
\[\phi(x,y_{1})+(1-\lambda)\phi(x_0,y_0)\leq \phi(x,y)+(1-\lambda)\phi(x,y_0)\]
(\(\lambda\)-FPP)
D E F I N I T I O N
The five-point property
(\forall y_0)(\exists \,x_0,y_1)(\forall x,y)
x_{0} = \displaystyle\argmin_{x\in X} \phi(x,y_{0})
y_{1} = \displaystyle\argmin_{y\in Y} \phi(x_0,y)
inspired by Csiszár–Tusnády ’84
Characterizes (AM):
Intrinsic, no regularity on \(X,Y,\phi,\mathbb{R}\)
If \(\phi\) satisfies the FPP then
\[\phi(x_n,y_n)\leq \phi(x,y)+\frac{\phi(x,y_0)-\phi(x_0,y_0)}{n}\]
If \(\phi\) satisfies the \(\lambda\)-FPP then
\[\phi(x_n,y_n)\leq \phi(x,y)+\frac{\lambda[\phi(x,y_0)-\phi(x_0,y_0)]}{\Lambda^n-1},\]
where \(\Lambda\coloneqq(1-\lambda)^{-1}>1\).
T H E O R E M (FL–PCAF '23)
Convergence rates
Proof.
(FPP) \(\iff\)
\[\phi(x_{n+1},y_{n+1}) \leq \phi(x,y) + [\phi(x,y_n)-\phi(x_n,y_n)] - [\phi(x,y_{n+1})-\phi(x_{n+1},y_{n+1})]\]
Sum from \(0\) to \(n-1\) implies
\[n\,\phi(x_n,y_n) \leq n\,\phi(x,y) + [\phi(x,y_0)-\phi(x_0,y_0)] - [\phi(x,y_{n})-\phi(x_{n},y_{n})]\]
🤔
\[\phi(x_0,y_0)\leq \phi(x,y)+\phi(x,y_0)-\phi(x,y_{1})\]
(\forall y_0)(\exists \,x_0,y_1)(\forall x,y)
Transition to geometry
How to obtain the FPP
Answer: when \(X,Y\) smooth manifolds, find a path \((x(t),y(t))\) joining \((x_0,y_1)\) to \((x,y)\) such that
\(b(t)=\phi(x(t),y(t))+\phi(x(t),y_0)-\phi(x(t),y_{1})\) is convex.
Why: special structure of the FPP
(FPP) \(\iff b(0)\leq b(1)\)
and \(b'(0)=0\)
1. Alternating minimization
2. The Kim–McCann geometry
3. Applications
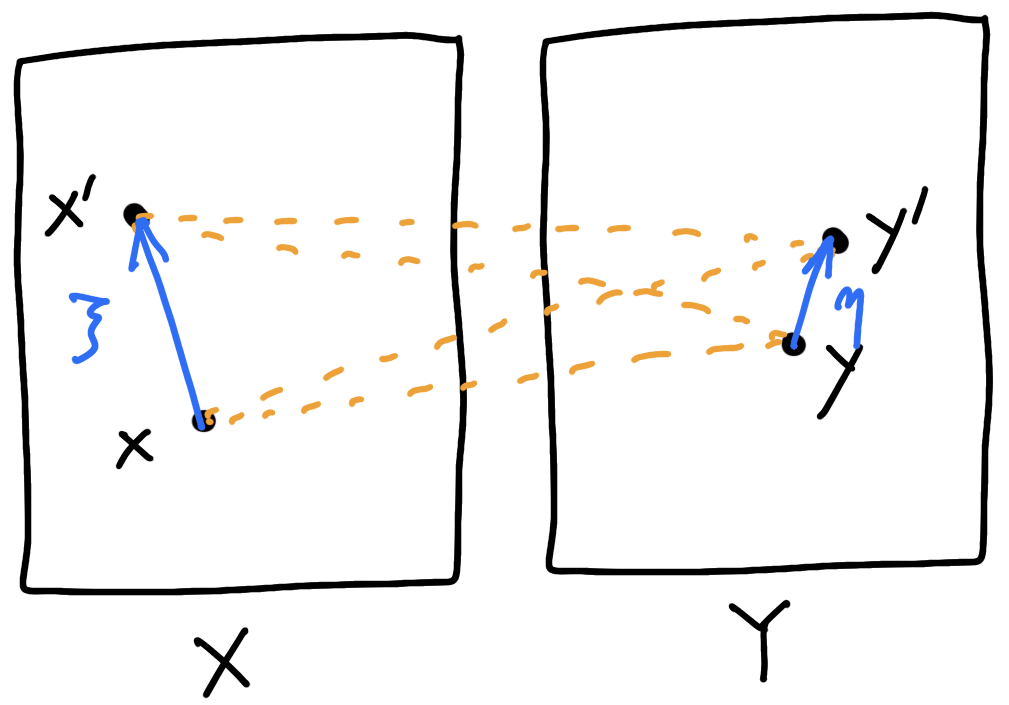
Pseudo-Riemannian metric on \(X\times Y\)
(Kim–McCann ’10)
D E F I N I T I O N : The Kim–McCann metric
\[g_{\scriptscriptstyle\text{KM}}=\frac12\begin{pmatrix}0 & -\nabla^2_{xy}c(x,y)\\-\nabla^2_{xy}c(x,y) & 0\end{pmatrix}\]
\(\delta_c(x+\xi,y+\eta;x,y)=\underbrace{-\nabla^2_{xy}c(x,y)(\xi,\eta)}_{\text{Kim--McCann metric ('10)}}+o(\lvert\xi\rvert^2+\lvert\eta\rvert^2)\)
\(\delta_c(x',y';x,y)=\)
\([c(x,y')+c(x',y)]-[c(x,y)+c(x',y')]\)
\(X, Y\): \(d\)-dimensional smooth manifolds
\(c\in C^4(X\times Y)\)
➡ \(c\)-segments: Kim–McCann geodesics \((x(t),y)\)
➡ cross-curvature: curvature of the Kim–McCann metric (aka MTW tensor)
T H E O R E M (Kim–McCann '11)
Under some assumptions on \((X,Y,c)\),
nonnegative cross-curvature \(\iff t\mapsto c(x(t),y)-c(x(t),y')\) is convex for any \(c\)-segment \((x(t),y)\).
\(c\)-segments and cross-curvature
A local criteria for the five-point property
Suppose that \(c\) has nonnegative cross-curvature.
T H E O R E M (FL–PCAF '23)
\(X, Y\): \(d\)-dimensional smooth manifolds
\(c\in C^4(X\times Y), \,\, g\in C^1(X),\,\, h\in C^1(Y)\)
\phi(x,y)=c(x,y)+g(x)+h(y)
If \(F(x)\coloneqq\inf_{y\in Y}\phi(x,y)\) is convex on every \(c\)-segment \(t\mapsto (x(t),y)\) satisfying \(x(0)=\argmin_{x\in X} \phi(x,y)\), then \(\phi\) satisfies the FPP.
"... \(F(x)-\lambda\phi(x,y)\) ..." \(\leadsto\) \(\lambda\)-FFP.
Intrinsic: \(c\)-segments and \(F\).
1. Alternating minimization
2. The Kim–McCann geometry
3. Applications
Riemannian/metric space setting
da Cruz Neto, de Lima, Oliveira ’98
Bento, Ferreira, Melo ’17
2. Explicit: \(\phi(x,y)=\frac{1}{2\tau} d_M^2(x,y)+h(y),\quad f(x)=\inf_y\phi(x,y)\)
\[x_{n+1}=\exp_{x_n}\big(-\tau\nabla f(x_n)\big)\]
\(\operatorname{Riem}\geq 0\): \(\nabla^2f\geq 0\) gives \(O(1/n)\) convergence rates
\(\operatorname{Riem}\leq 0\): if \(d_M^2(x,y)\) has nonpositive cross-curvature then convexity of \(f\) on \(c\)-segments gives \(O(1/n)\) convergence rates
Riemannian manifold \(X=Y=M\)
1. Implicit: \(\phi(x,y)=\frac{1}{2\tau} d_M^2(x,y)+f(x)\)
\[x_{n+1}=\argmin_{x} f(x)+\frac{1}{2\tau}d_M^2(x,x_n)\]
\(\operatorname{Riem}\leq 0\): \(\nabla^2f\geq 0\) gives \(O(1/n)\) convergence rates
\(\operatorname{Riem}\geq 0\): if \(d_M^2(x,y)\) has nonnegative cross-curvature then convexity of \(f\) on \(c\)-segments gives \(O(1/n)\) convergence rates
Wasserstein gradient flows, generalized geodesics (Ambrosio–Gigli–Savaré '05)
Global rates for Newton's method
Newton's method: new global convergence rate.
New condition on \(F\) similar but different from self-concordance
T H E O R E M (FL–PCAF '23)
If \(F\) is convex on the paths \(x(t)=(\nabla u)^{-1}(y(t))\) with \(y(t)\) standard segments, then
\[F(x_n)\leq F(x)+\frac{u(x_0|x)}{n}\]
\(\longrightarrow\) Natural gradient descent:
\[x_{n+1}-x_n=-\nabla^2u(x_n)^{-1}\nabla F(x_n)\]
\begin{aligned}
\phi(x,y)&=u(y|x)+h(y)\\
F(x)&=\inf_y\phi(x,y)
\end{aligned}
Thank you!
Reference:
Gradient descent with a general cost. Flavien Léger and Pierre-Cyril Aubin-Frankowski. arXiv:2305.04917, 2023
(SIGMA-MODE 2024-01-30) A geometry for alternating minimization
By Flavien Léger
