Suites arithmétiques -
Suites géométriques



Les suites arithmétiques correspondent à des évolutions linéaires.


Méthode : Pour montrer qu'une suite \((u_n)\) est arithmétique de raison r, il faut montrer que pour tout entier n on a :
Ce qui équivaut à :


On en déduit que \((u_n)\) est une suite arithmétique de raison r = 2
et de premier terme \(u_0=2\times 0+3=3\).
ou


Méthode : Pour montrer qu'une suite \((u_n)\) n'est pas arithmétique, on peut montrer que :

On en déduit que \((u_n)\) est une suite arithmétique de raison \(r=\dfrac{3}{2}\)
et de premier terme \(u_0=\dfrac{3\times 0+1}{2}=\dfrac{1}{2}\).



donc par définition \((u_n)\) est une suite arithmétique de raison \(r=-2\)
et de premier terme \(u_0=2\).


4. a.


5
u \(-\) 3
u
u

Python
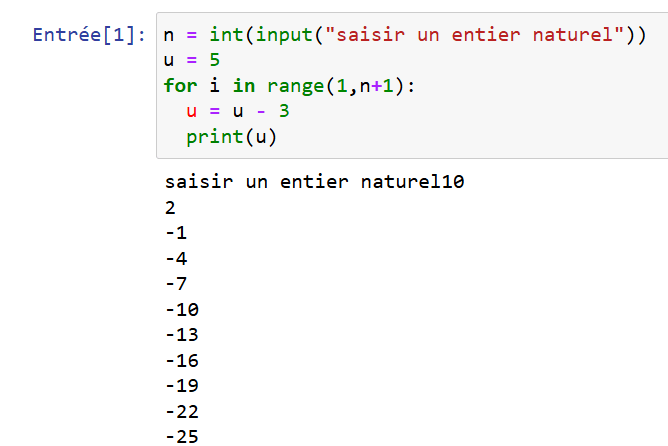















On demande la formule explicite de la suite \((u_n)\).



On a donc :
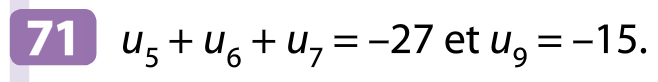
On a donc :
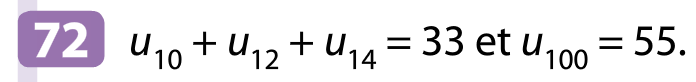
On a donc :




On a donc :






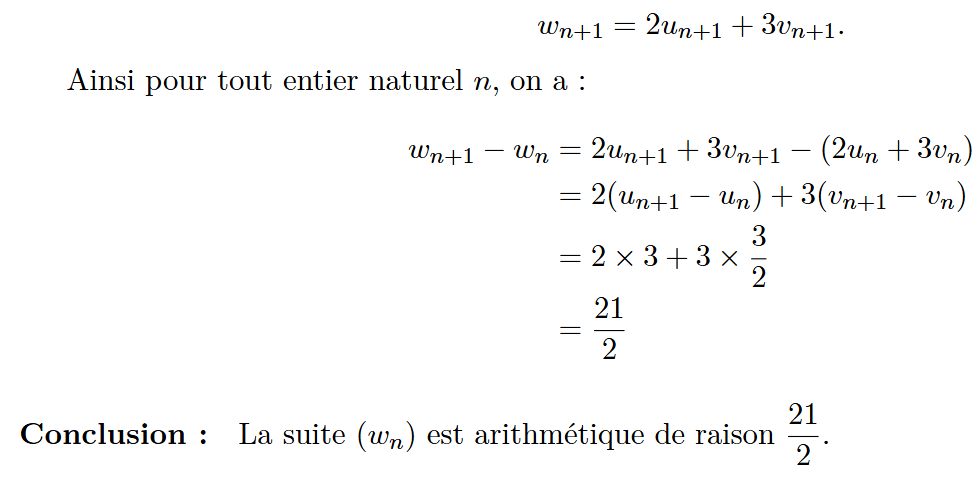
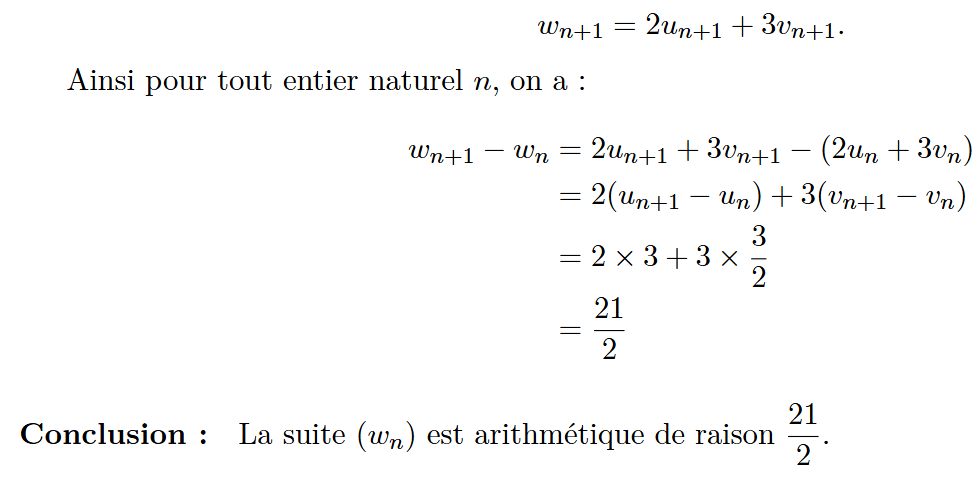
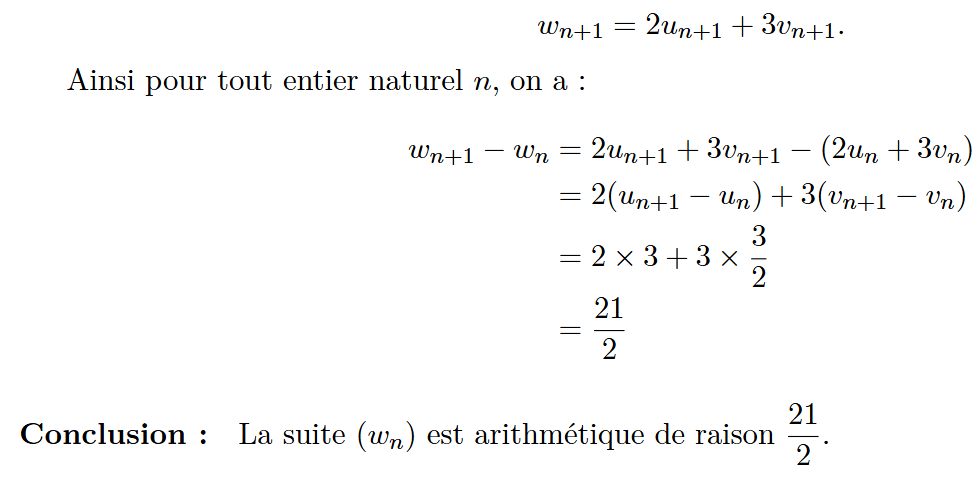



Somme de termes d'une suite arithmétique :



On exprime chaque terme en fonction de \(u_0\) et de r.
Ce qui nous donne :
Puis en divisant par 3 les deux membres de la première équation, on obtient :
Résolution du système :
Résolution du système avec la méthode par combinaisons :
On soustrait membre à membre les deux équations et on obtient :
On soustrait membre à membre les deux équations et on obtient :
Résolution du système :
Résolution du système avec la méthode par substitution :
Dans la première équation on exprime \(u_0\) en fonction de \(r\) :
Dans la deuxième équation on substitue à \(u_0\) l'expression obtenue :
On résout cette dernière équation :
On détermine la deuxième inconnue :

b) On commence par calculer le dernier terme de la somme :


bis
On commence par calculer le dernier terme de la somme :

bis
On commence par calculer le dernier terme de la somme :



Les suites géométriques correspondent à des évolutions exponentielles.

Méthode : Pour montrer qu'une suite \((u_n)\) est géométrique de raison q, il faut montrer que pour tout entier n on a :
Ce qui équivaut à :

On en déduit que \((u_n)\) est une suite géométrique de raison \(q=5\)
et de premier terme \(u_0=5^ {0+3}=125\).
ou

ou
On en déduit que \((u_n)\) est une suite géométrique de raison \(q=\dfrac{1}{3}\)
et de premier terme \(u_0= \dfrac{2}{3^{0+1}}=\dfrac{2}{3}\).

Méthode : Pour montrer qu'une suite \((u_n)\) n'est pas géométrique, on peut montrer que :











On commence par calculer la raison q :

On commence par calculer la raison q :


bis


Calcul du premier terme de la somme :
Le nombre de termes de la somme est 5 donc

Calcul du premier terme de la somme :
Le nombre de termes est 7 donc

On note \(u_1\) l'aire du premier disque : \(u_1=16 \pi\)
L'aire du deuxième est \(u_2=4 \pi\)...
\( (u_n) \) est une suite géométrique de raison \(\dfrac{1}{4} \).

28)








29)






30)






31)







31 bis )
Suites arithmétiques - Suites géométriques
By Jean-Marc Kraëber
Suites arithmétiques - Suites géométriques
Première - Spécialité
- 3,723



