Dérivation


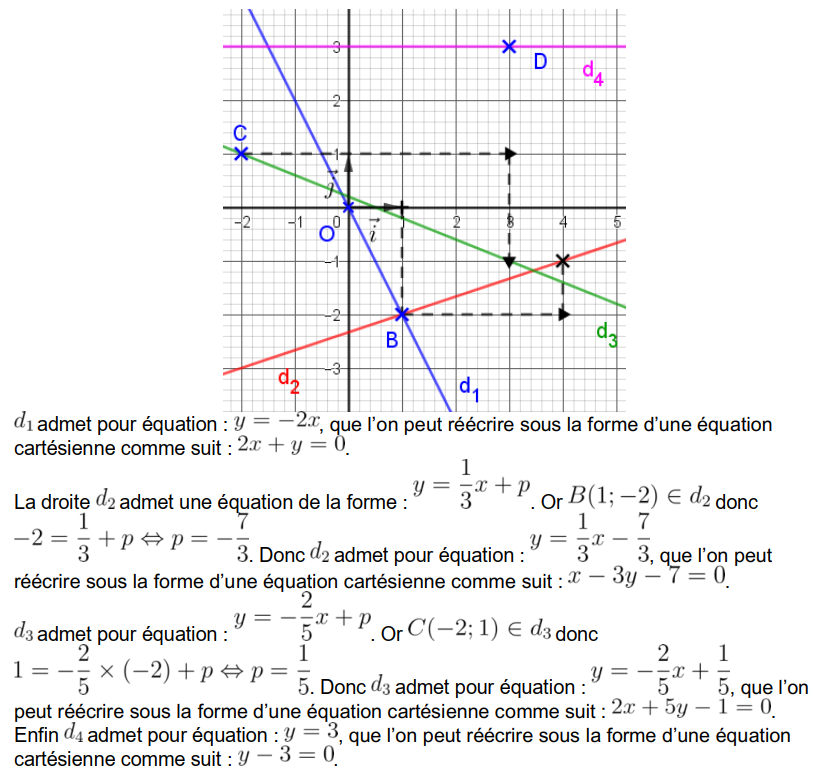
| (La droite \(d_4\) passe par la point de coordonnées (3 ; 3)) |

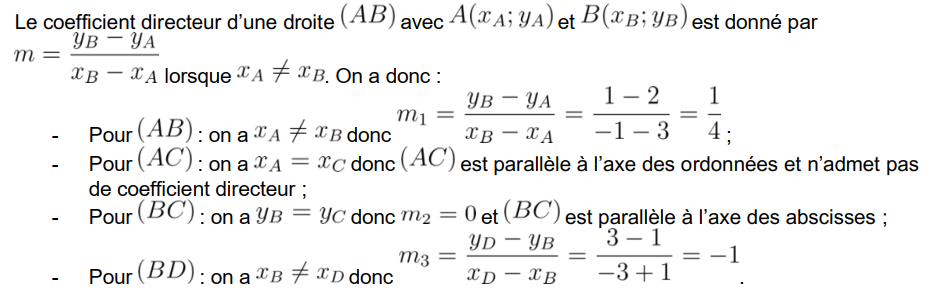






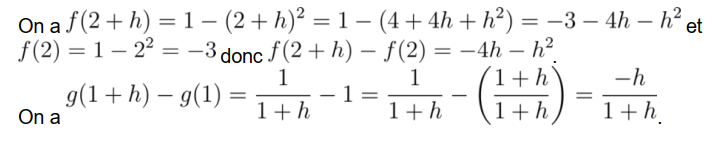

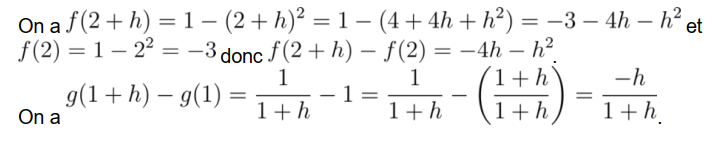
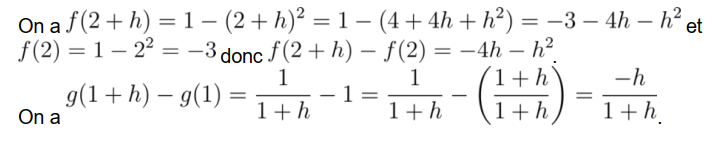
Comprendre la dérivation

La limite de \(-h-3\) quand \(h\) tend vers 0 est égale à \(-3\) donc \(f\) est dérivable en 2 et \(f'(2)=-3\).
3. A la calculatrice :




La limite de \(12+6h+h^2\) quand \(h\) tend vers 0 est égale à \(12\) donc \(f\) est dérivable en 2 et \(f'(2)=12\).
3. A la calculatrice :


La limite de \(\dfrac{-1}{1+h}\) quand \(h\) tend vers 0 est égale à \(-1\) donc \(f\) est dérivable en 1 et \(f'(1)=-1\).
La limite de \(\dfrac{-1}{2(2+h)}\) quand \(h\) tend vers 0 est égale à \(-\dfrac{1}{4}\) donc \(f\) est dérivable en 2 et
\(f'(2)=-\dfrac{1}{4}\).
On en déduit que


\(f'(1)\) est le coefficient directeur de la tangente à la courbe au point A d'abscisse 1, c'est à dire la droite (AB).

On remplace m par \(-\dfrac{25}{4}\) dans l'équation de \(T_B\) :
On en déduit que \(p=-\dfrac{21}{4}\).
3. \(T_B\) a pour coefficient directeur \(f'(-1)=-\dfrac{25}{4}\) .
\(T_C\) a pour coefficient directeur \(f'(3)=-\dfrac{101}{12}\) .
\(-\dfrac{25}{4}\neq -\dfrac{101}{12}\) donc \(T_B\) et \(T_C\) ne sont pas parallèles.

Équation réduite de la tangente à \(C_f\) au point d'abscisse \(a\) :
\(T_A\) admet pour équation réduite

Équation réduite de la tangente à \(C_f\) au point d'abscisse \(a\) :
\(T_B\) admet pour équation réduite

Équation réduite de la tangente à \(C_f\) au point d'abscisse \(a\) :
\(T_C\) admet pour équation réduite
Parcours orange




1. Équation réduite de la tangente à \(C_f\) au point d'abscisse \(4\) :


Calcul de \(f'(4)\) :
La limite de \(-h-6\) quand \(h\) tend vers 0 est égale à \(-6\) donc \(f'(4)=-6\).
L'équation réduite de la tangente à \(C_f\) au point d'abscisse \(4\) est donc
2. Pour étudier les positions relatives de \(\mathcal{C_f}\) et de sa tangente \(d\) on étudie le signe de \(f(x)-(-6x+24)\).
Soit
\(\Delta=0\) donc le trinôme est toujours du signe de a donc négatif et s'annule pour \(x_0=4\).
Conclusion : \(C_f\) est toujours située en-dessous sa tangente \(d\).
Pour étudier le signe du trinôme \(-x^2+8x-16\), on calcule son discriminant.

On en déduit que
La limite de \(6a+3h-2\) quand \(h\) tend vers 0 est égale à \(6a-2\) donc pour tout réel \(a\), \(f\) est dérivable en \(a\) et \(f'(a)=6a-2\).

1. a. Calcul de \(f'(-2)\) :
La limite de \(\dfrac{1}{2(h-2)}\) quand \(h\) tend vers 0 est égale à \(-\dfrac{1}{4}\) donc \(f'(-2)=-\dfrac{1}{4}\).
Avec un calcul similaire, on obtient \(f'(2)=-\dfrac{1}{4}\).
b. Équation réduite de la tangente à \(C_f\) au point d'abscisse \(-2\) :
Équation réduite de la tangente à \(C_f\) au point d'abscisse \(2\) :
c. Les deux tangentes ont le même coefficient directeur donc elles sont parallèles.
3. \(A'\) est le symétrique de \(A(a\;;f(a))\) par rapport à O donc ses coordonnées sont \((-a\;;-f(a))\).
La limite de \(\dfrac{-1}{a(a+h)}\) quand \(h\) tend vers 0 est égale à \(-\dfrac{1}{a^2}\) donc \(f'(a)=-\dfrac{1}{a^2}\) pour tout réel \(a\neq 0\).
On en déduit que
Les tangentes ont le même coefficient directeur donc elles sont parallèles.

On calcule \(f'(1)\) et \(g'(1)\) et on montre qu'ils sont égaux à \(-2\).
Cela prouve que \(C_f\) et \(C_g\) ont une tangente commune en A.

1. On a \(f(0) =0\). Calcul de \(f'(0)\) :
La limite de \(h^2-1\) quand \(h\) tend vers 0 est égale à \(-1\) donc \(f'(0)=-1\).
\(d\) la tangente à la courbe en O a donc pour équation réduite \(y=-x\).
2. On cherche à déterminer \(a\) l'abscisse du point A tel que \(g'(a)=-1\).
La limite de \(-2a-h+3\) quand \(h\) tend vers 0 est égale à \(-2a+3\) donc \(g'(a)=-2a+3\).
donc la tangente à \(C_g\) au point \(A(2\;;-2)\) a pour équation réduite
La tangente à \(C_g\) au point \(A(2\;;-2)\) est donc la droite \(d\).
Parcours vert
3 méthodes pour déterminer un nombre dérivé
- En calculant la limite d'un taux de variation : EX 42
- Par lecture graphique d'un coefficient directeur : EX 44, 47
- En calculant un coefficient directeur : Ex 48








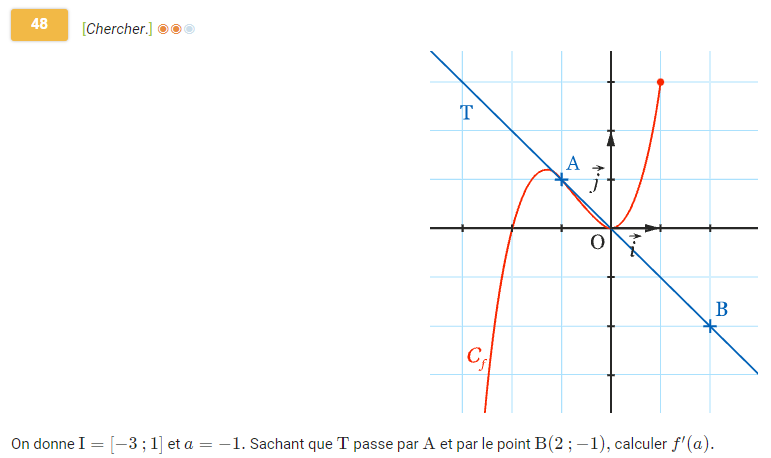



Équation réduite de la tangente à \(C_f\) au point d'abscisse \(a\) :
Équation réduite de la tangente à \(C_f\) au point d'abscisse 1 :

Équation réduite de la tangente à \(C_f\) au point d'abscisse 2 :








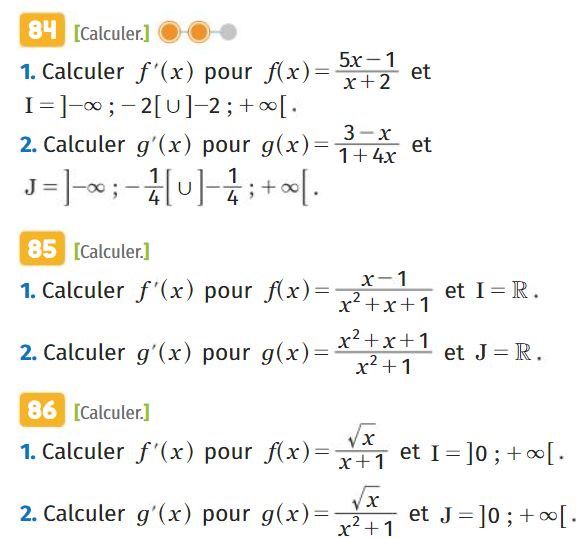
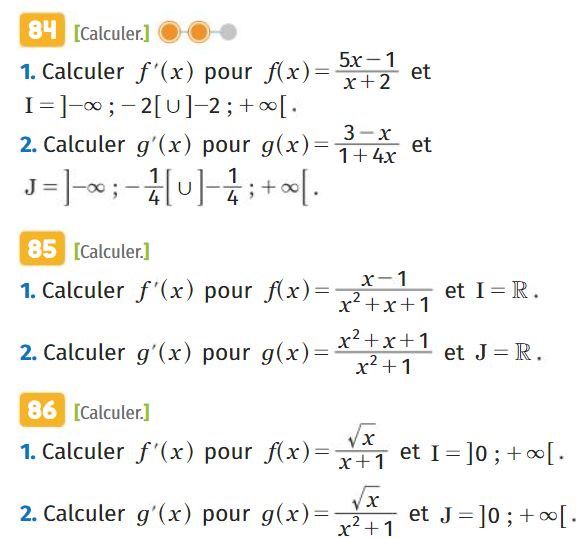
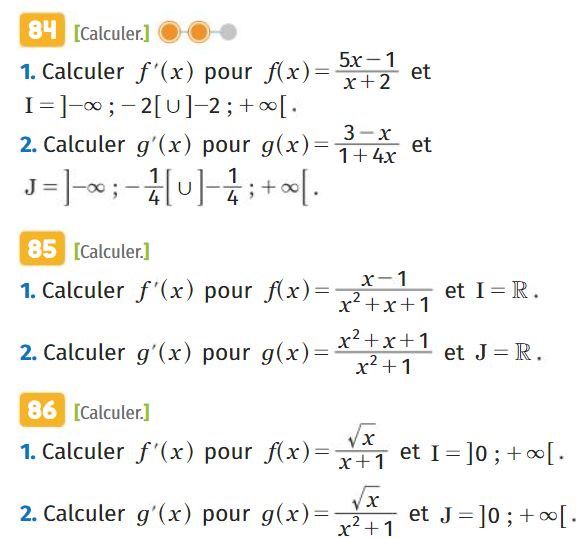
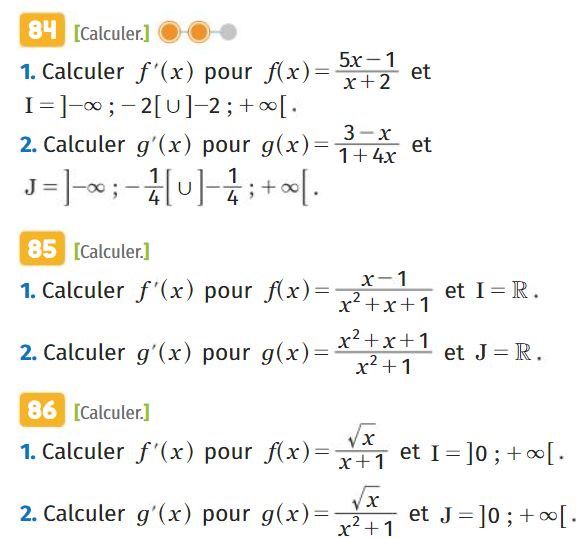
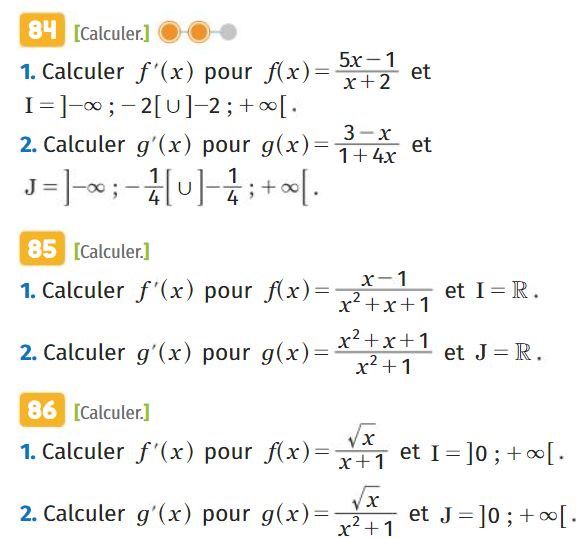
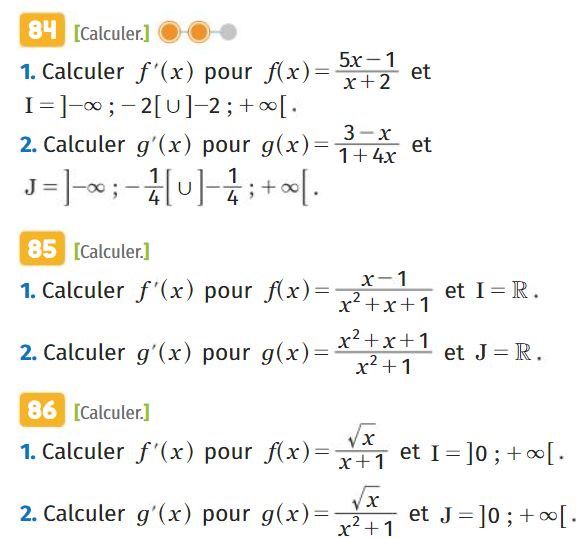




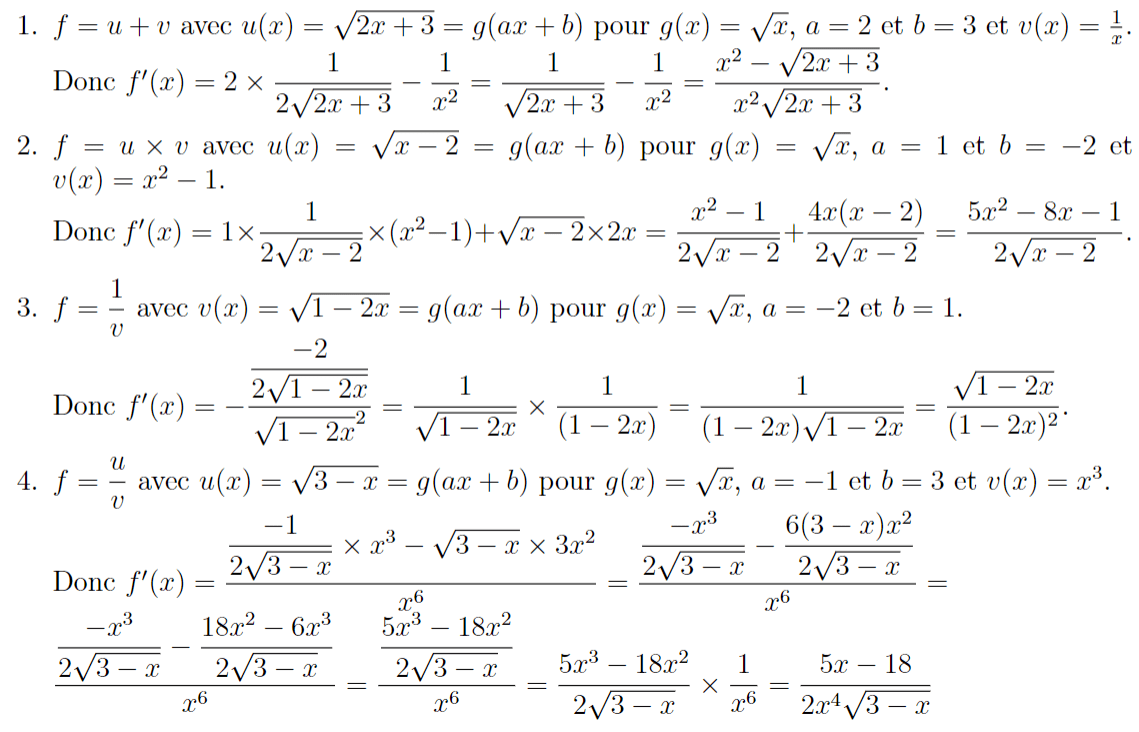

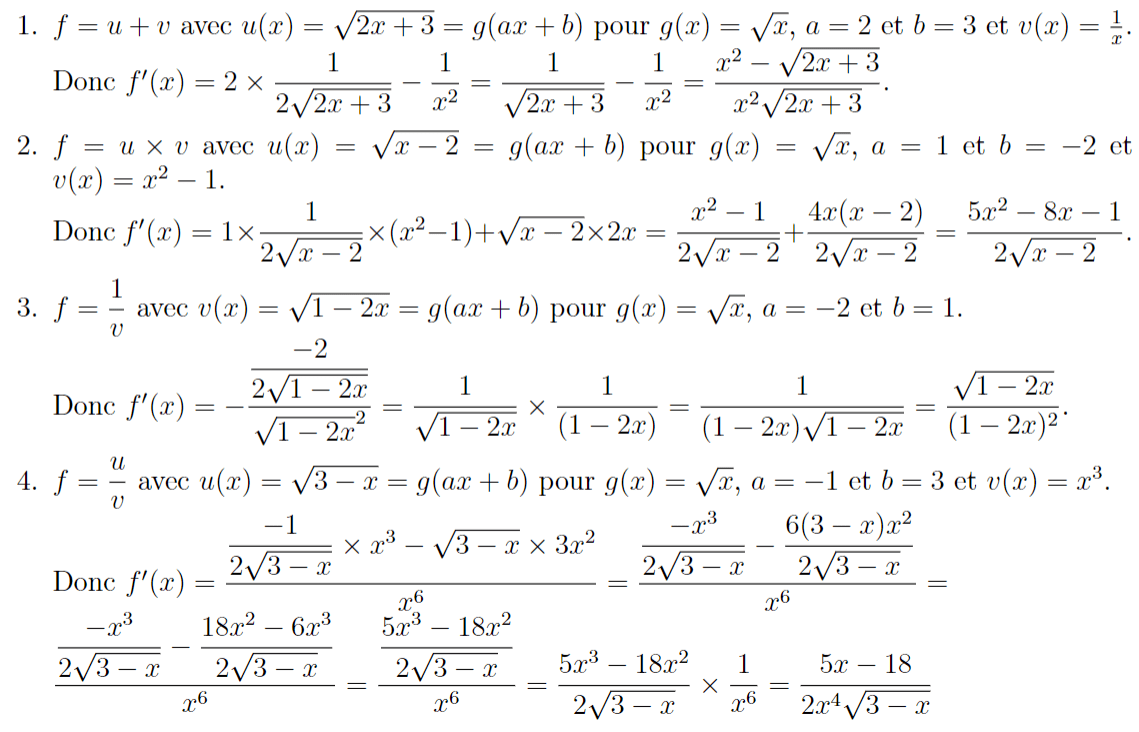


Dérivation : Exercices
By Jean-Marc Kraëber
Dérivation : Exercices
Première Spécialité
- 2,403



