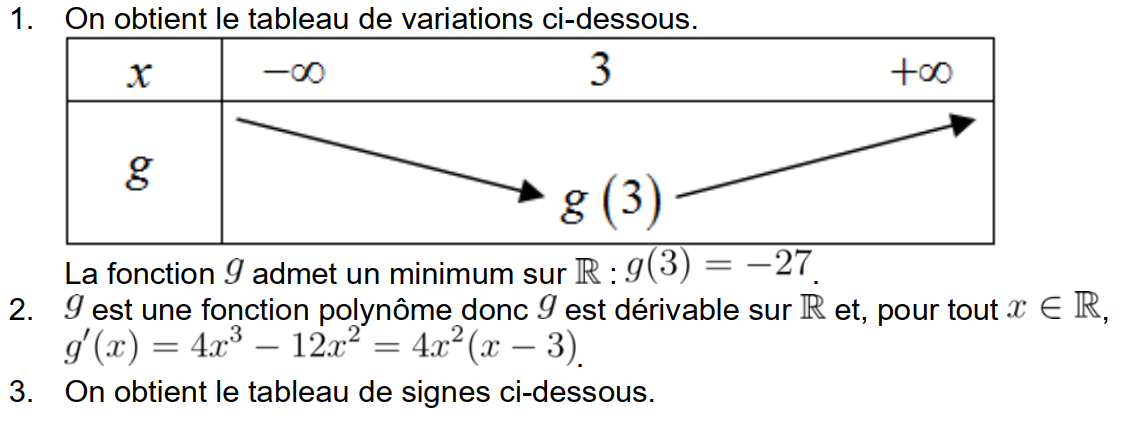
Applications de la dérivation
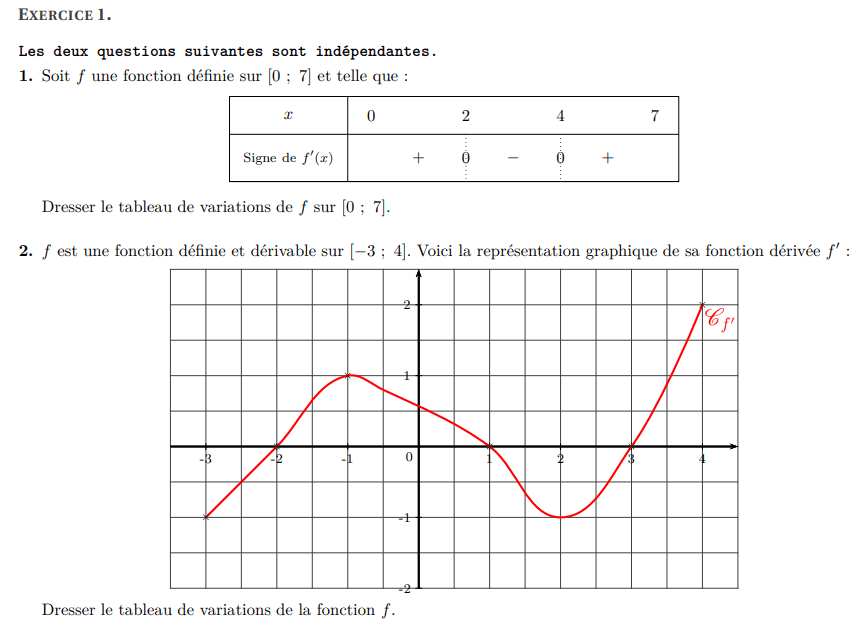
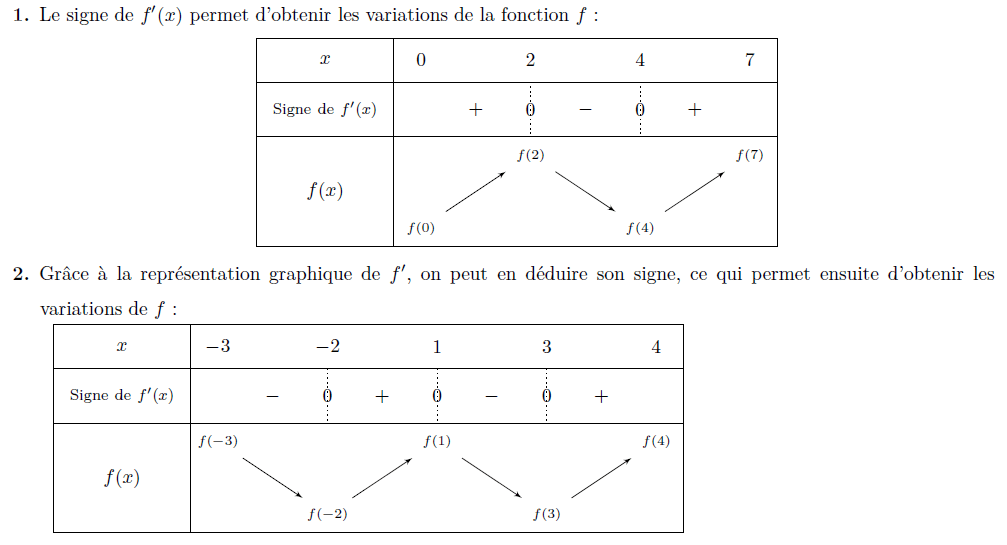
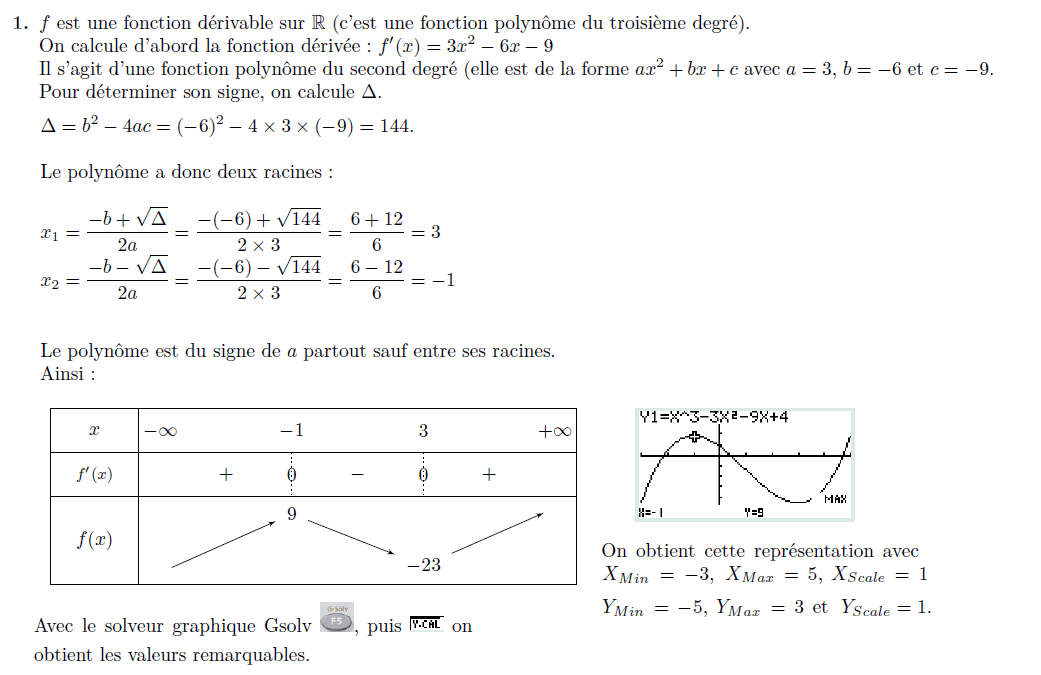
h est une fonction polynôme donc elle est dérivable sur \(\R\). On calcule d'abord la fonction dérivée :
h'(x)=3x^2-6x-9
On étudie ensuite le signe de h', la fonction dérivée :
La fonction h', est du signe de a donc positive à l'extérieur de ses racines.
h(-1)=9
h(3)=-23
).
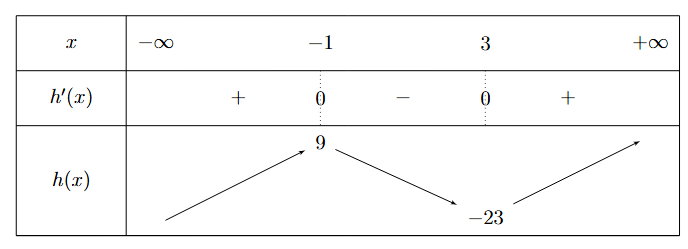
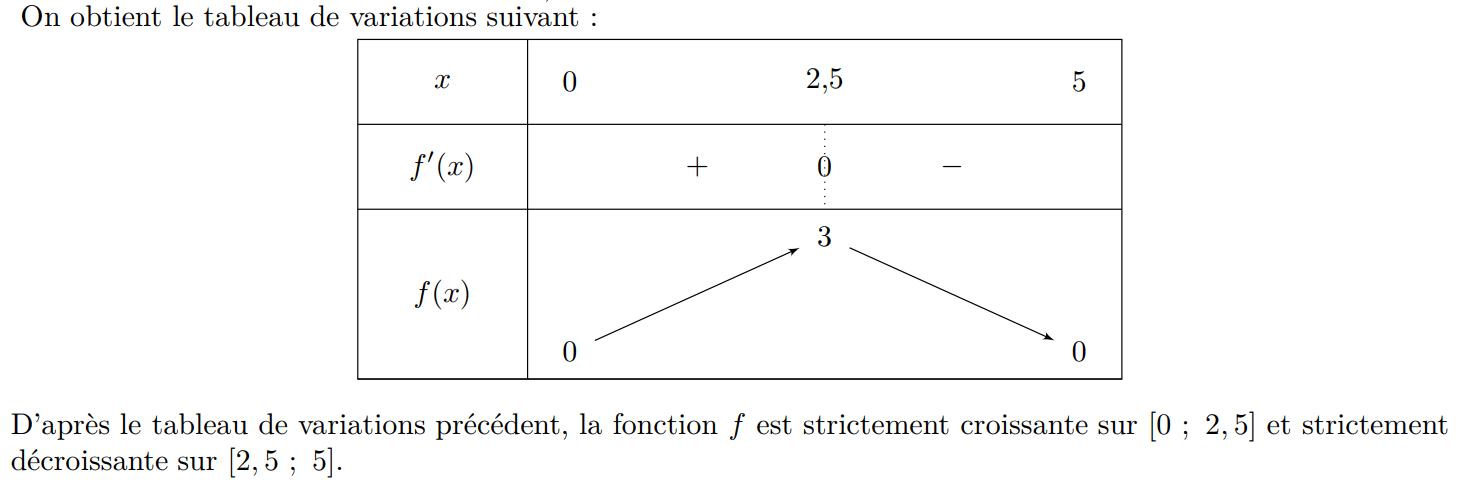
On en déduit le tableau de variations de la fonction h :
On vérifie avec la calculatrice :
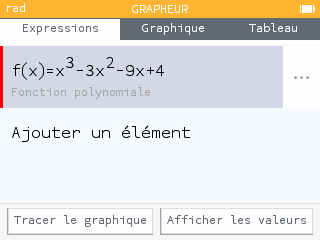
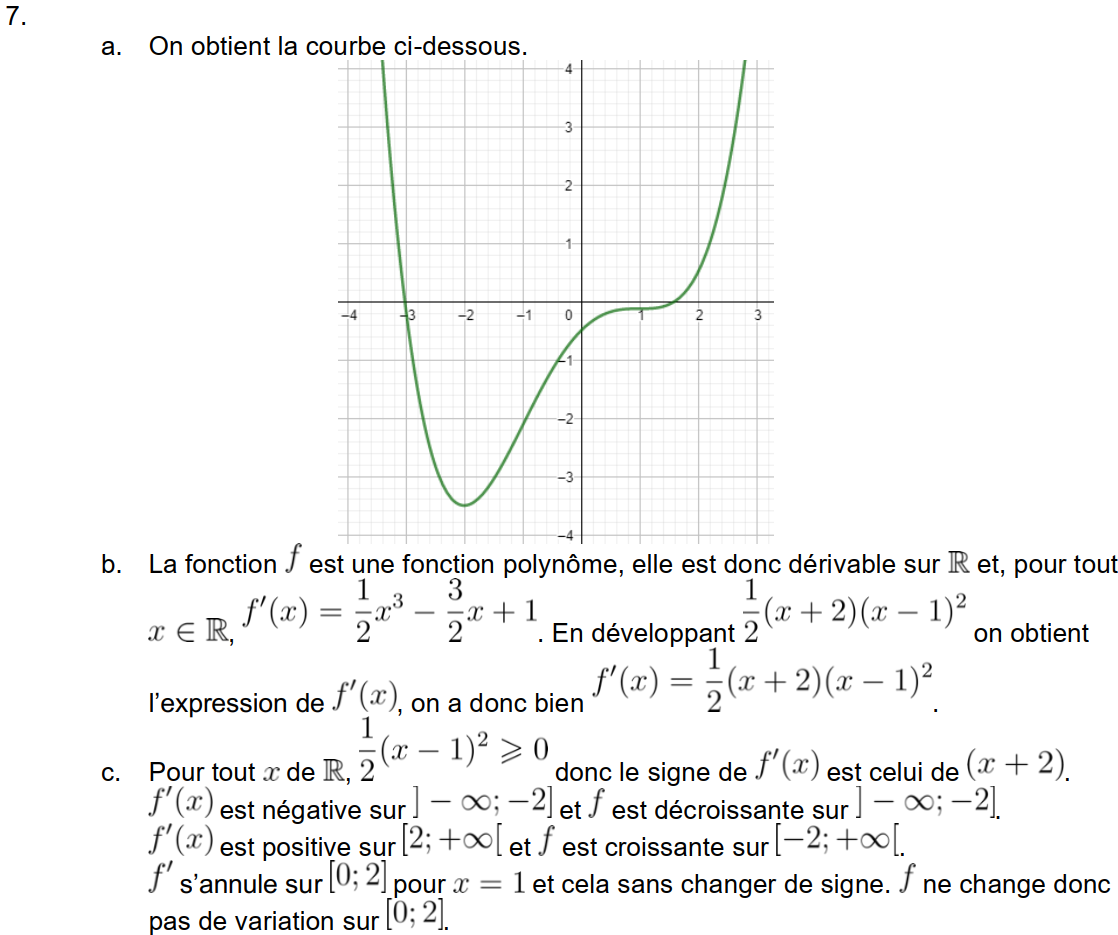
Calcul de la dérivée :
Signe de la dérivée :
\text{Pour tout réel }x\text{ de}\in ]-2\,;+\infty[, (4x+8)^2>0\text{ donc }g'(x)>0.
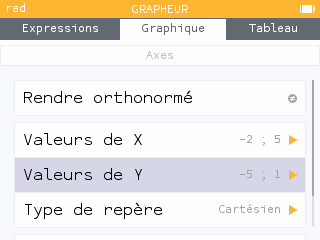
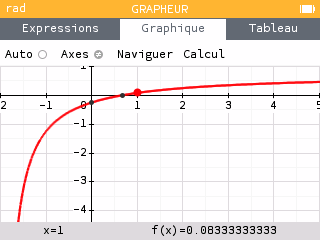
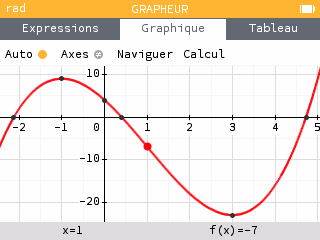
Axes :
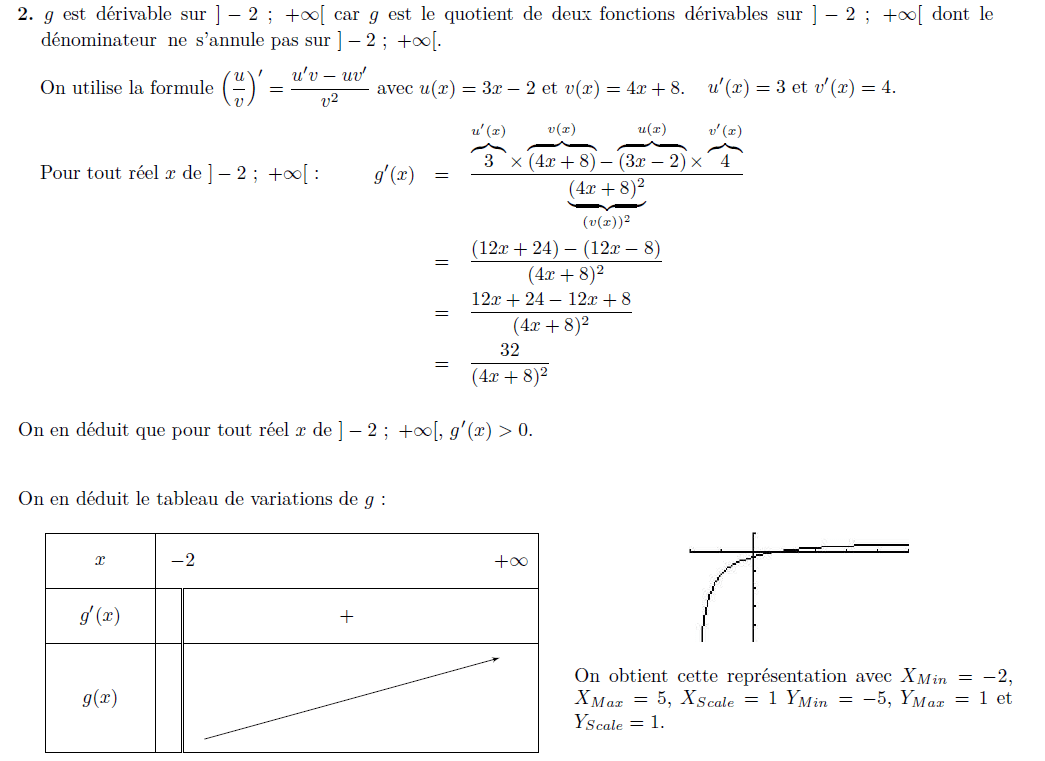
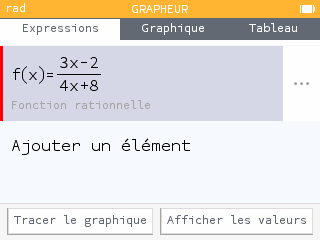
Calcul de la dérivée (avec mise au même dénominateur) :
Signe de la dérivée :
\text{Pour tout réel }x\text{ de}\in \R^*, x^2>0\text{ donc }f'(x)\text{ est du signe de }2x^2-1.
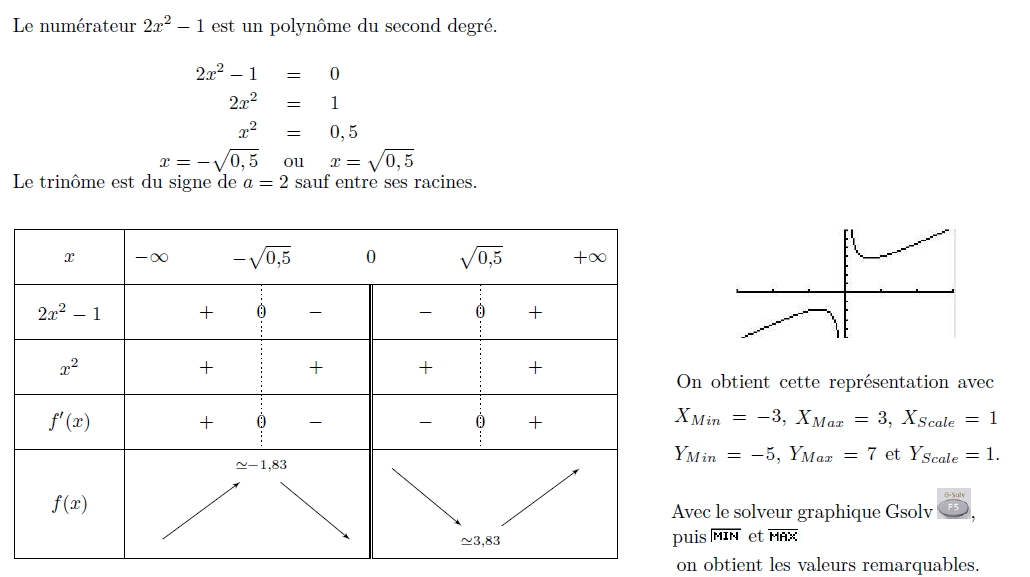
Il est du signe de a, donc positif, à l'extérieur de ses racines.
(\text{avec }a=2, b=0 \text{ et }c=-1)
(\text{ou calcul de }\Delta)
Tableau de variations :
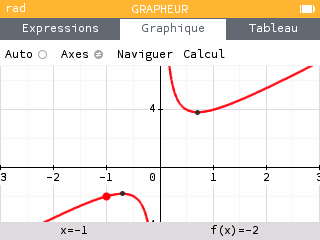
Calcul de la dérivée :
Signe de la dérivée :
Tableau de variations :
f'(x)=6x^2-18x-24
Calcul de la dérivée :
Le polynôme \(f'(x)\) est du signe de a, donc positif, à l'extérieur de ses racines.
D'après les calculs précédents, \(f\) admet un maximum local, \(53\), atteint pour \(x=-1\) et un minimum local, \(-72\), atteint pour \(x=4\).
D'après le tableau de variations de \(f\), lorsque \(x\in [-2\,;3]\), \(-59\leqslant f(x)\leqslant 53 \).
Le polynôme \(h'(x)\) est du signe de a, donc positif, à l'extérieur de ses racines.
f'(x)=0 \text{ équivaut à }x = 0 \text{ ou }
Le polynôme \(f'(x)\) est du signe de a, donc négatif, à l'extérieur de ses racines.
Calcul de la dérivée :
Signe de la dérivée :
On développe f pour ne pas avoir à utiliser la formule (uv)'=u'v+uv'
On factorise f' pour avoir les racines sans utiliser \(\Delta\)
y = -x+1
x
f(x)
mx+p
f(x)>mx+p
f(x)-(mx+p)>0
x
f(x)
mx+p
f(x)< mx+p
f(x)-(mx+p)<0
f(x)-(mx+p)
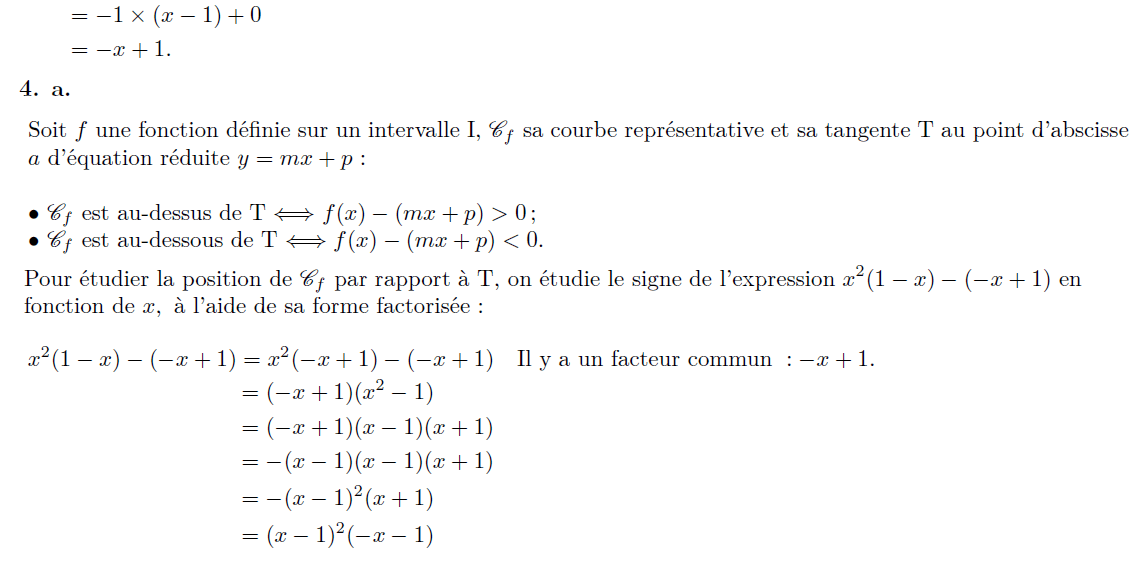
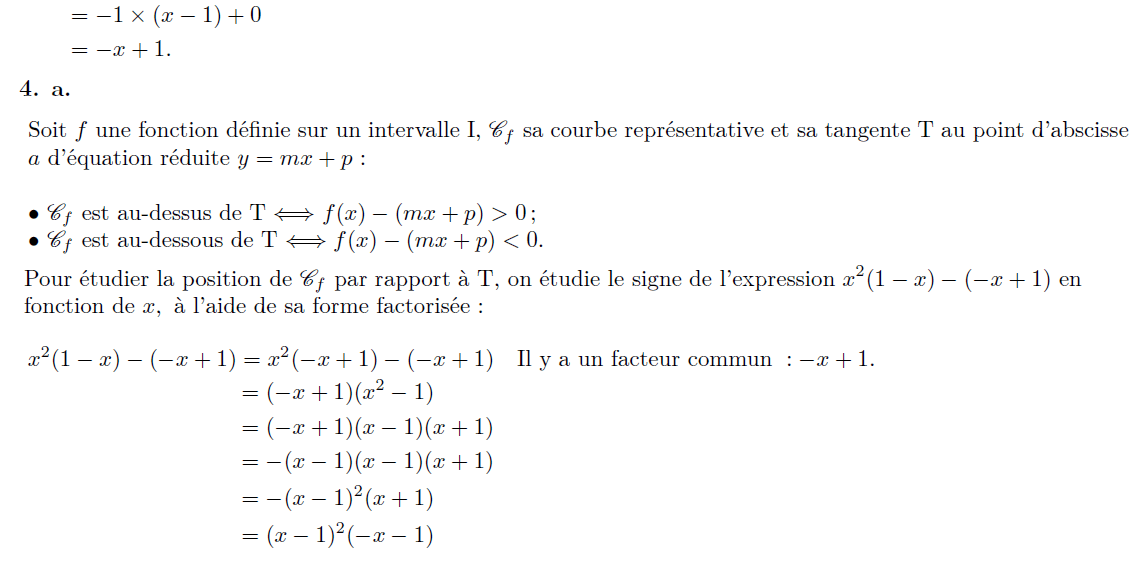
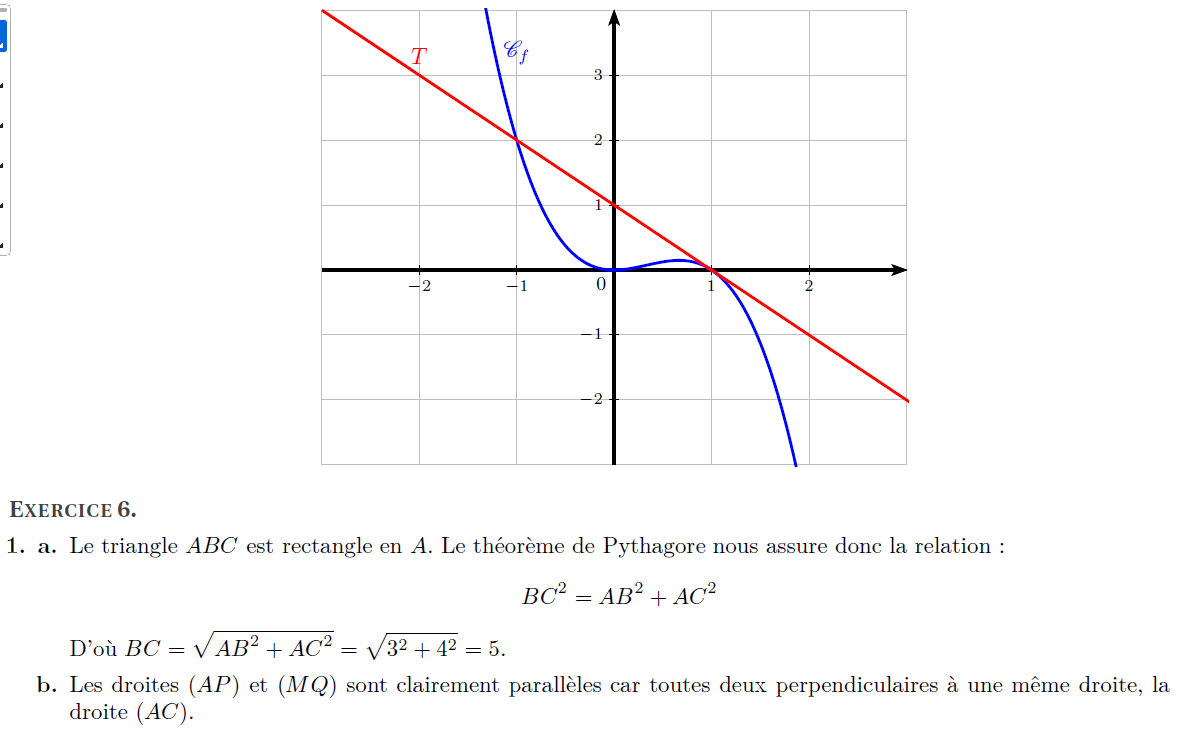
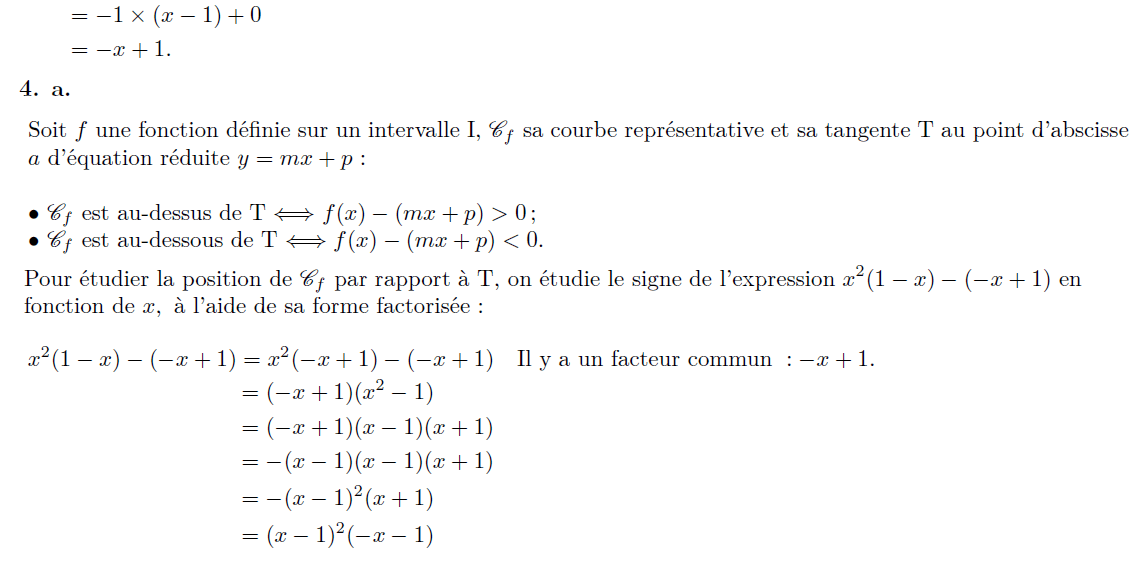
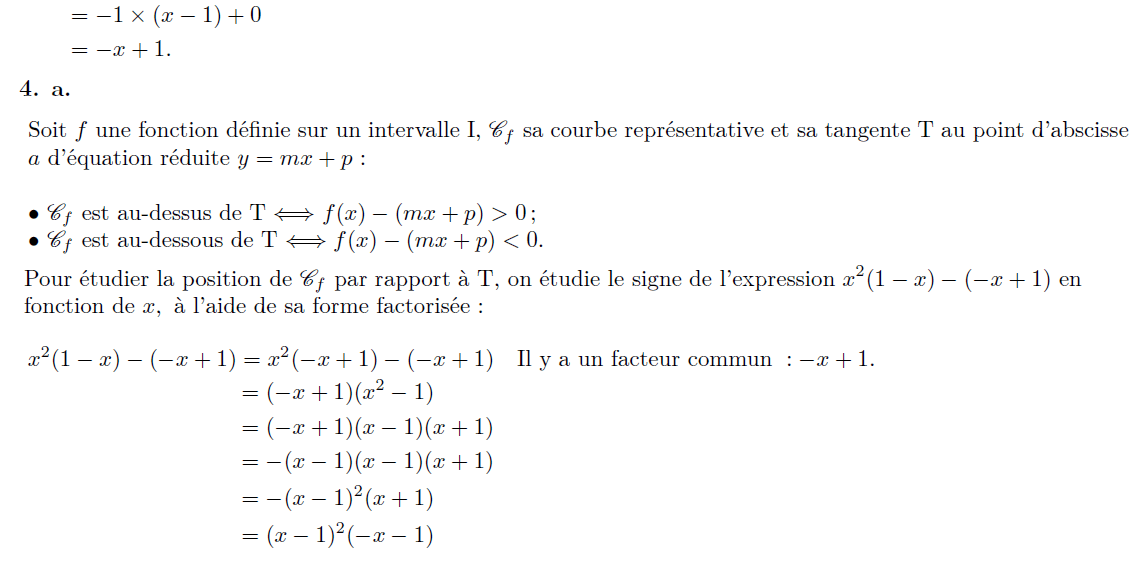
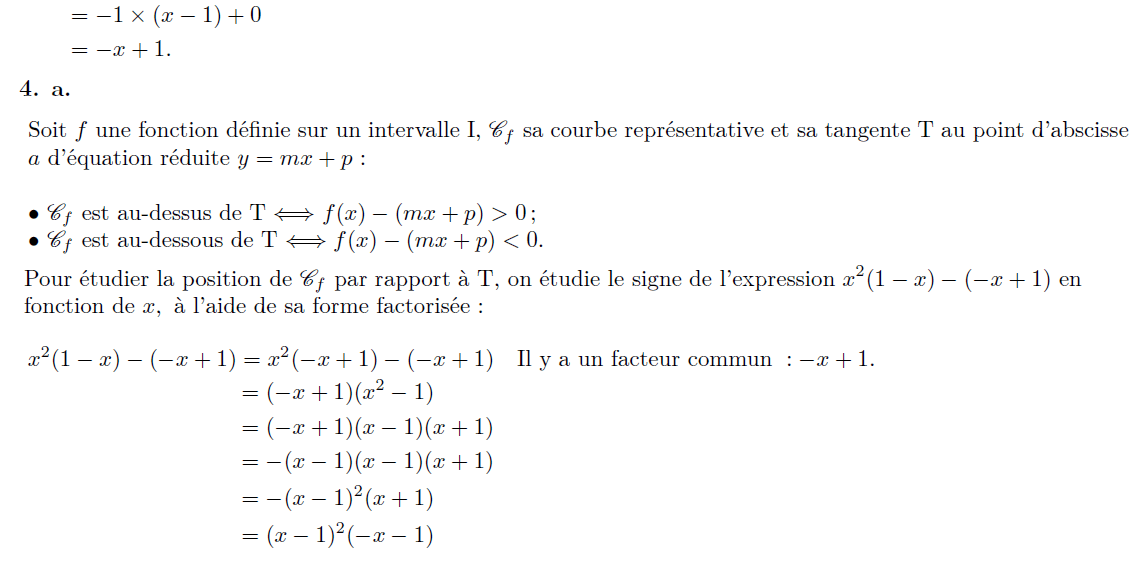
Méthode à retenir :
\text{Ici, }f(x)= x^2(1-x)\text{ et }mx+p = -x+1
f(x)-(mx+p)= x^2(1-x)-(-x+1)
\times 1
k\times a-k\times b
k( a- b)
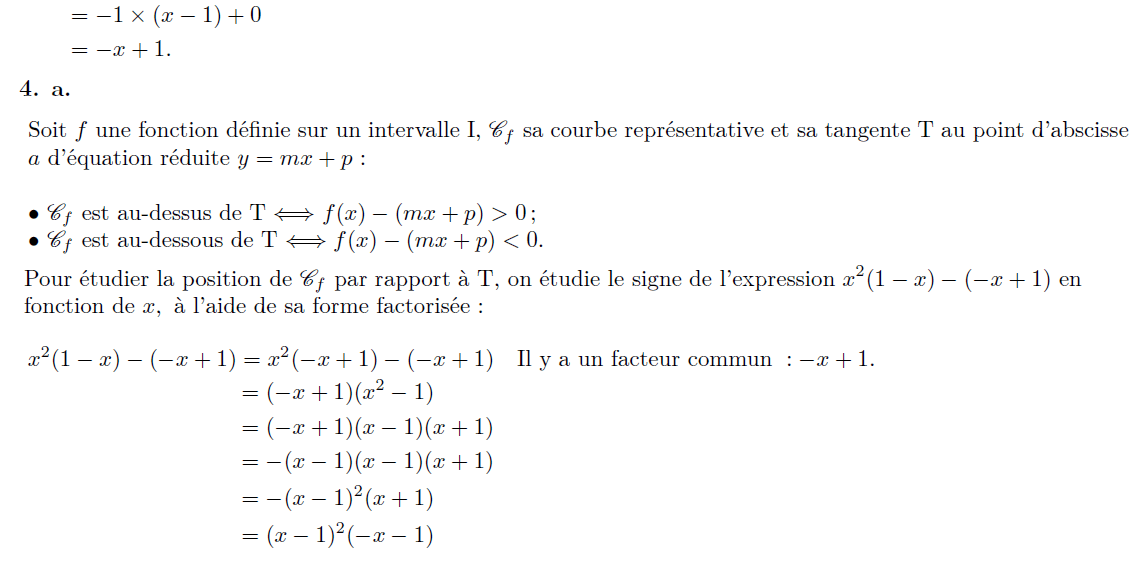
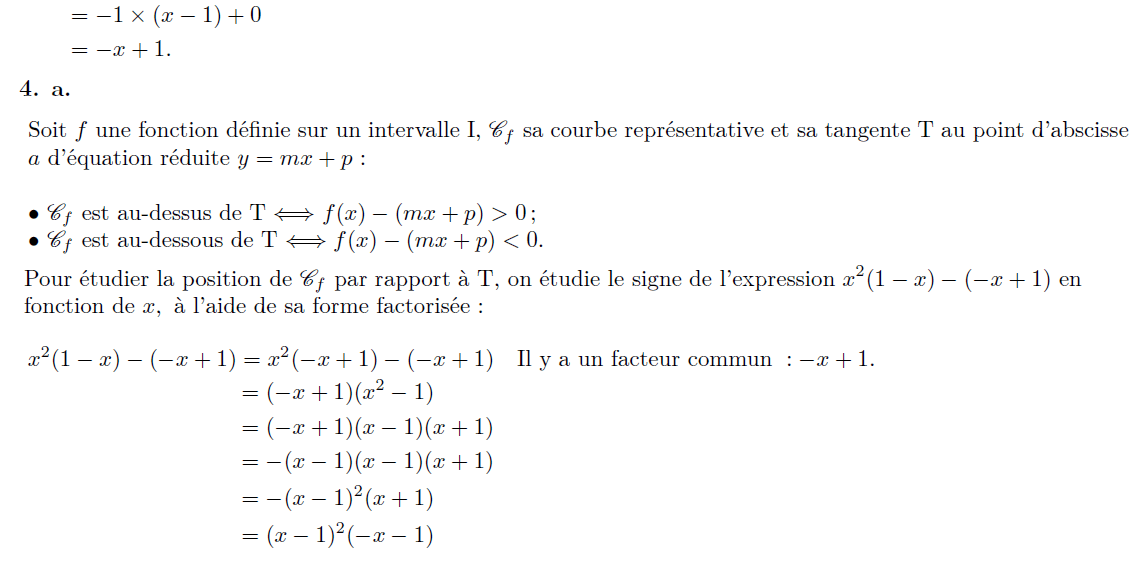
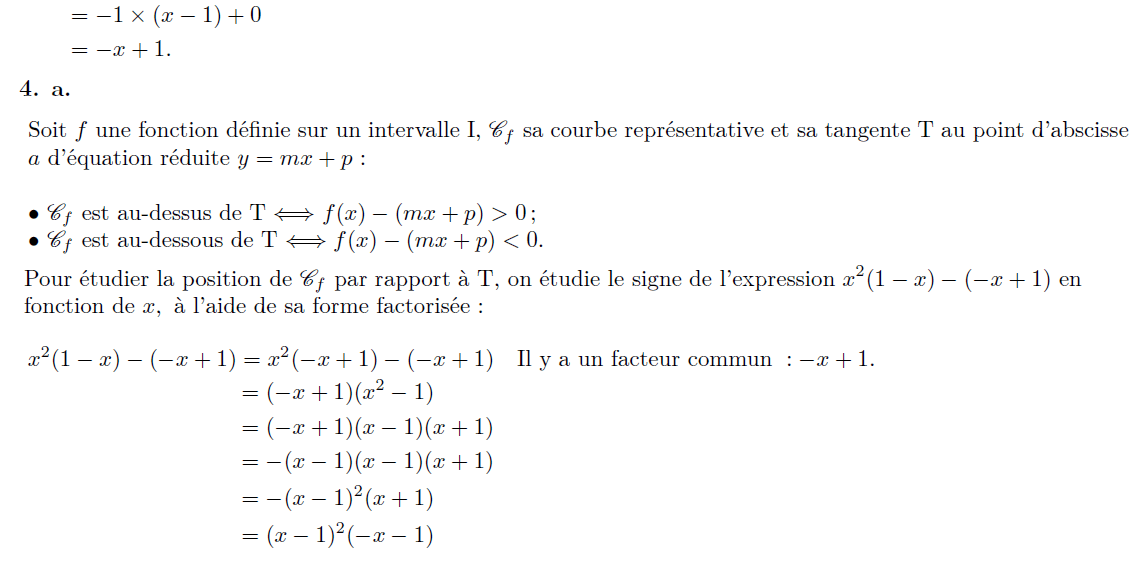
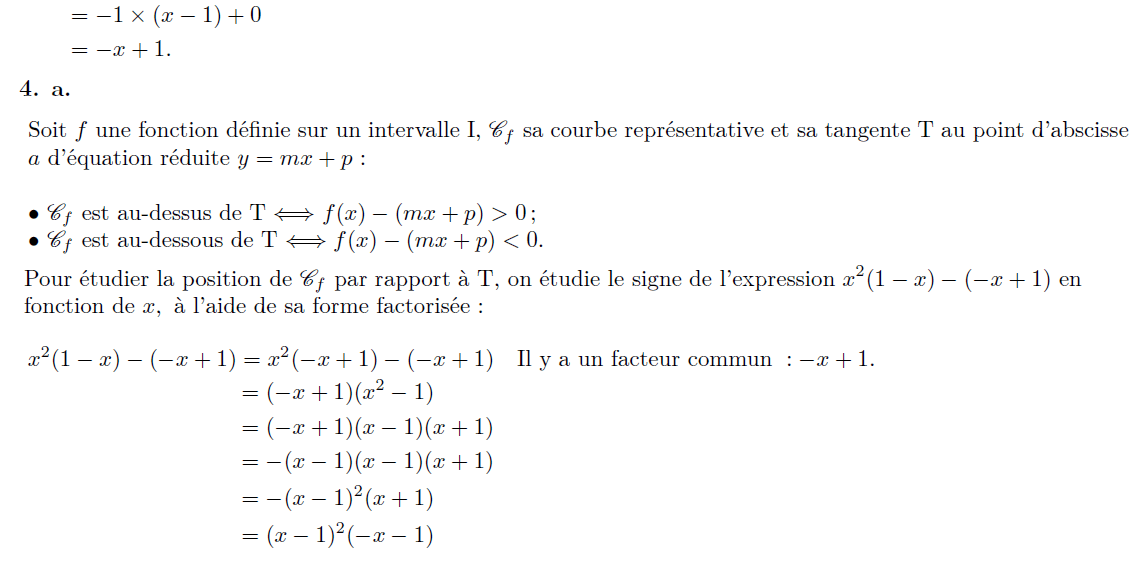
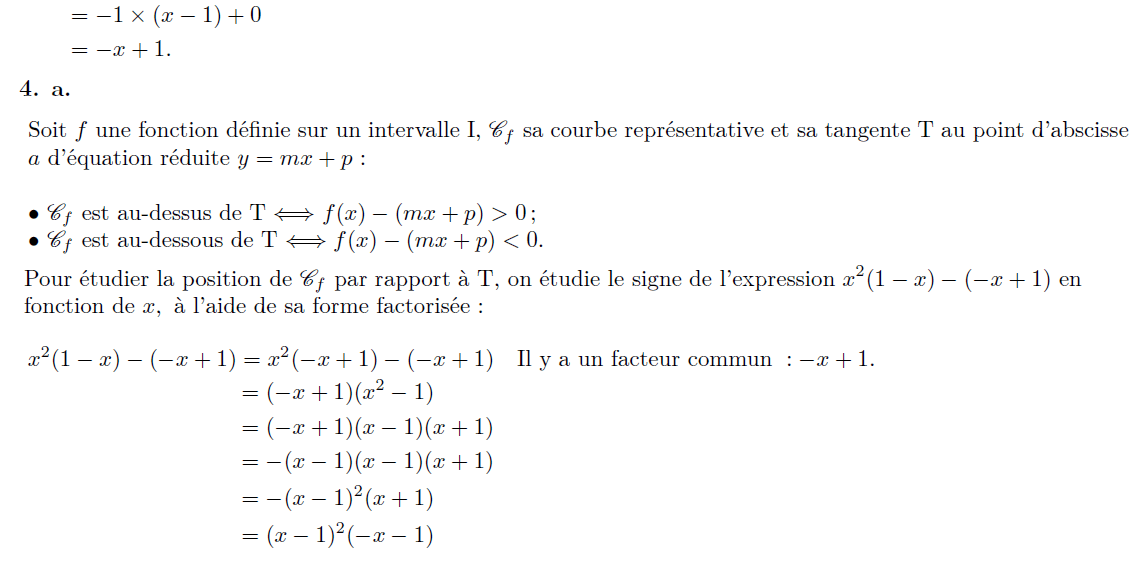
Signe ?
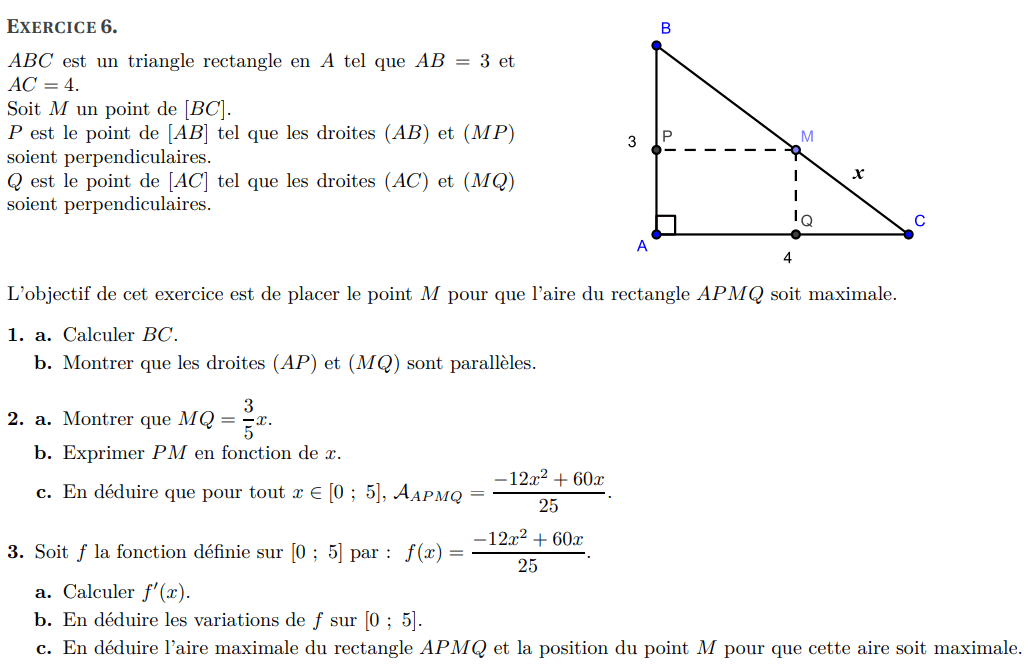
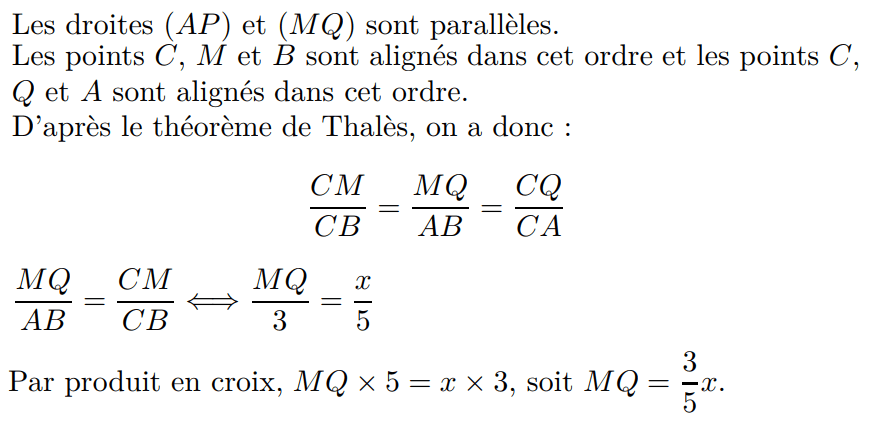
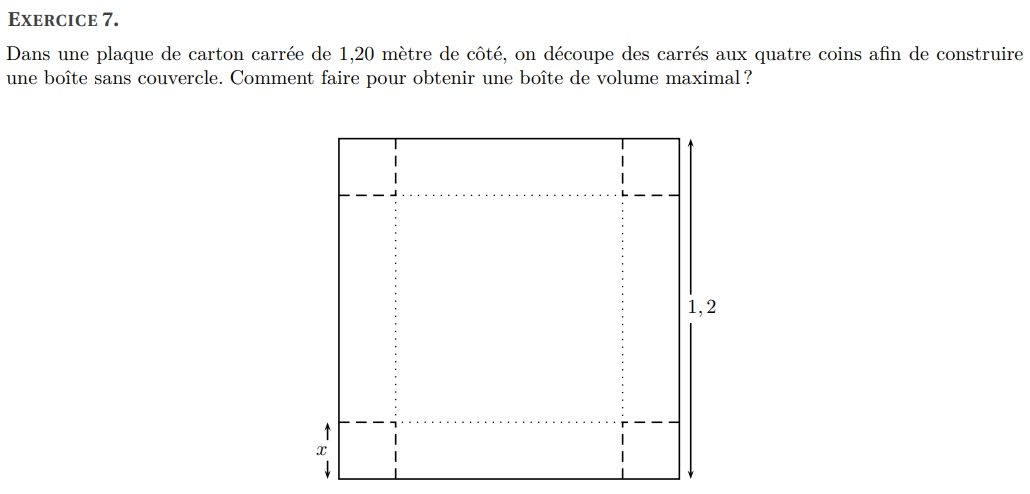
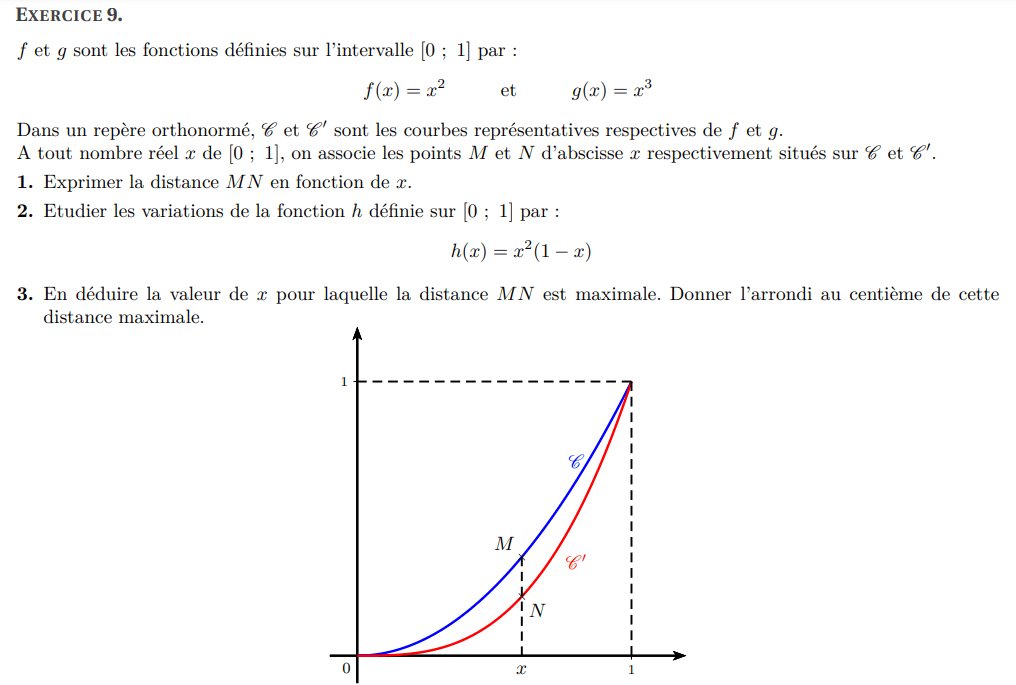
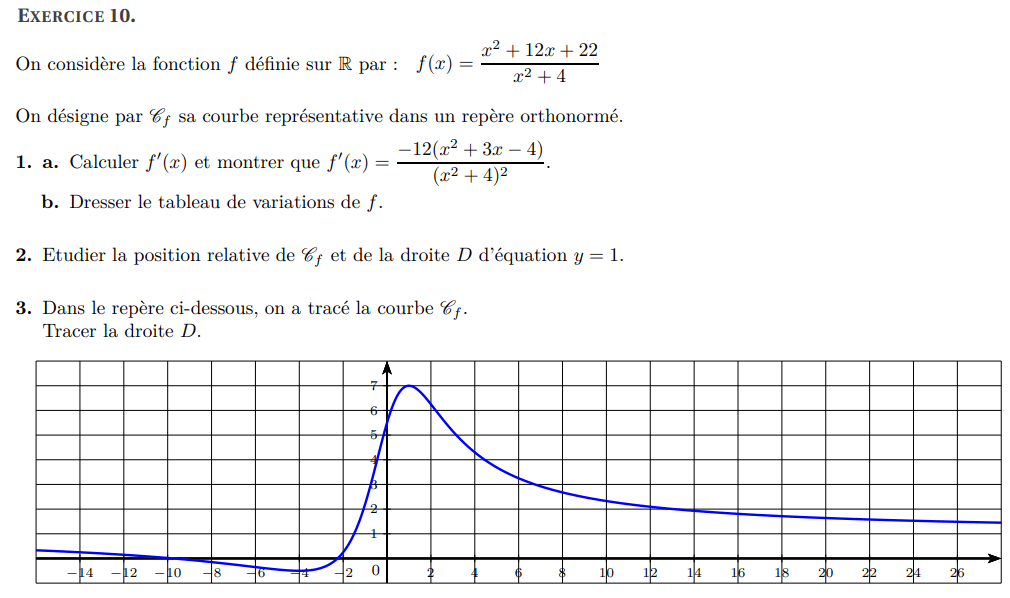
Calcul de la dérivée :
Signe de la dérivée :
Tableau de variations :
Applications de la dérivation
Version 2024
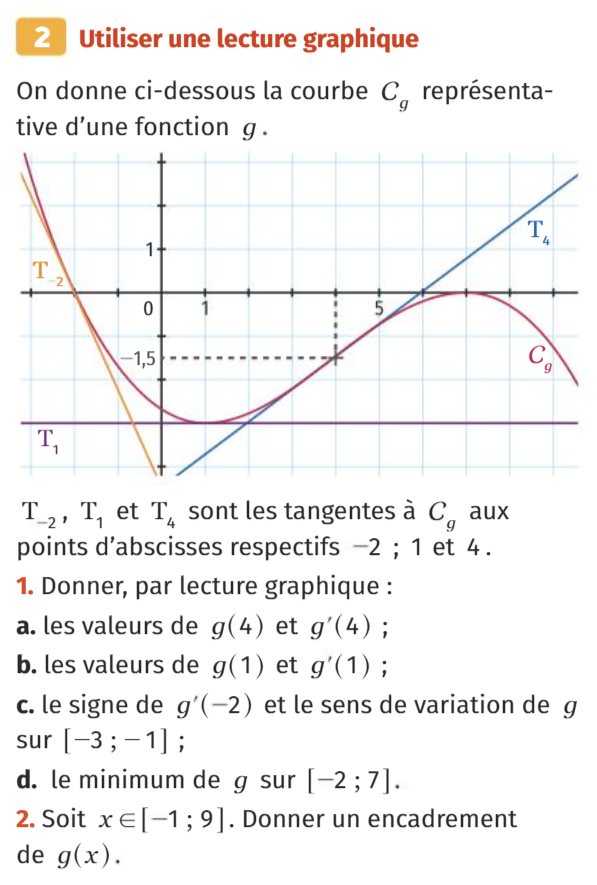
d. Le minimum de \(g\) sur \([-2~;~7]\) est 0 ; il est atteint pour \(x=1\).
\text{2. Si }x\in [-1~;~9]\text{ alors }-3\leqslant g(x)\leqslant 0.
Corrigé sur Overleaf
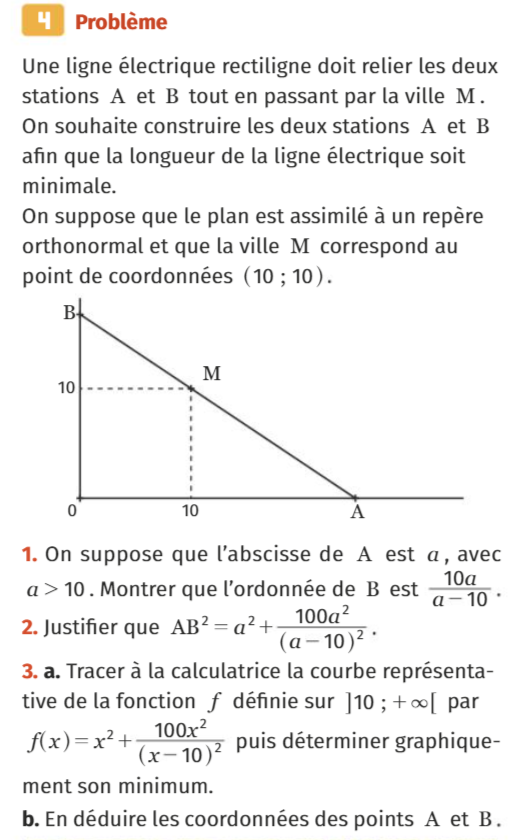
Corrigé sur Overleaf
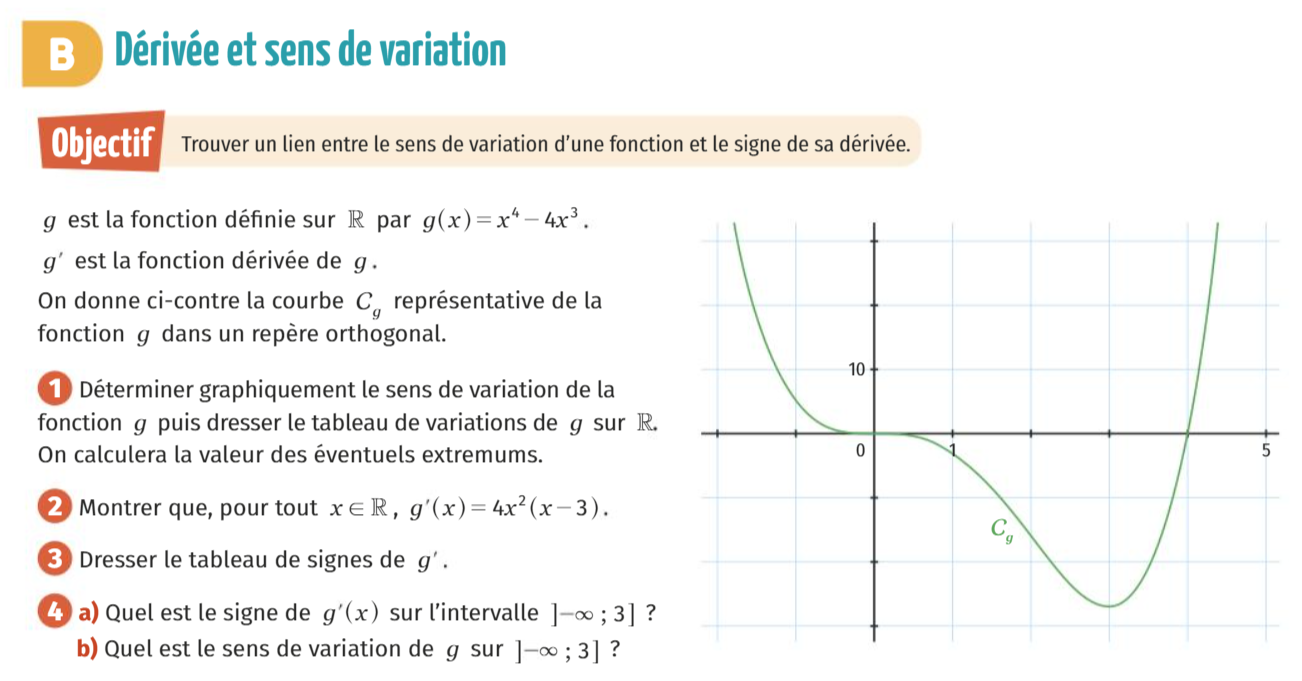
On peut conjecturer qu’une fonction dérivable est décroissante sur un intervalle si et seulement si sa dérivée est inférieure ou égale à 0 ; et qu’une fonction dérivable est croissante sur un intervalle si et seulement si sa dérivée est supérieure ou égale à 0.
Notion d'extremum local
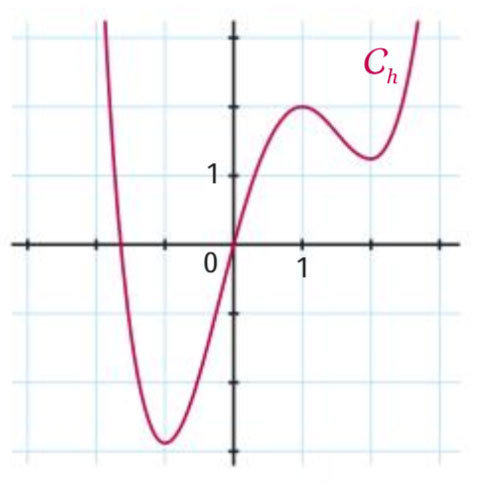
Savoir reconnaître un extremum local graphiquement :
la fonction \(h\) représentée ci-contre admet un maximum local en 1 : \(h(1)\)
h(1)
Autour de 1 (on dit "au voisinage de 1),
les images des nombres juste avant 1 et juste après 1 sont inférieures à \(h(1)\)
localement, le point de coordonnées (1 ; h(1)) est le sommet de la courbe
"Avant 1", \(h\) est croissante. "Après 1" \(h\) est décroissante : localement la fonction \(h\) a atteint un maximum.
Il y a un changement du sens de variation de la fonction.
Suite
la fonction \(h\) représentée ci-contre admet un minimum local en 2 : \(h(2)\)
h(2)
Au voisinage de 2, les images des nombres juste avant 2 et juste après 2 sont supérieures à \(h(2)\)
localement, le point de coordonnées (2 ; h(2)) est le plus bas de la courbe.
2
"Avant 2", \(h\) est décroissante. "Après 2" \(h\) est croissante : localement la fonction \(h\) a atteint un minimum.
Il y a un changement du sens de variation de la fonction.
Savoir reconnaître un extremum local à partir d'un tableau de variations :
Une fonction admet un extremum local lorsque sa dérivée s'annule et change de signe.
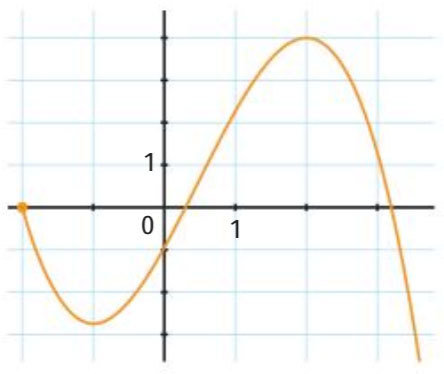
Exemple : Soit la fonction \(f\) définie sur \([-2\,;+\infty[\) par \(f(x) = -0,5x^3+0,75x^2+3x-1\).
On veut déterminer les valeurs de \(x\) pour lesquelles la fonction admet un extremum local :
Savoir déterminer un extremum local à partir de l'expression algébrique d'une fonction :
Conjecture :
- \(f\) admet un minimum local pour \(x=-1\)
- \(f\) admet un maximum local pour \(x=2\)
Pour le démontrer on détermine les variations de la fonction en étudiant le signe de la dérivée...
f'(x)=-1,5x^2+1,5x+3
1. On détermine \(f'\) :
\Delta = 20,25\,;\quad x_1=-1\text{ et }x_2=2.
Règle du signe d'un trinôme : \(f'\) est négative \( (a = -1,5) \) à l'extérieur de ses racines. D'où le tableau de variations :
2. On détermine le signe de \(f'\) :
Applications de la dérivation
By Jean-Marc Kraëber
Applications de la dérivation
Lycée Saint-Exupéry de La Rochelle
