Calcul littéral
Et un peu de calcul numérique...
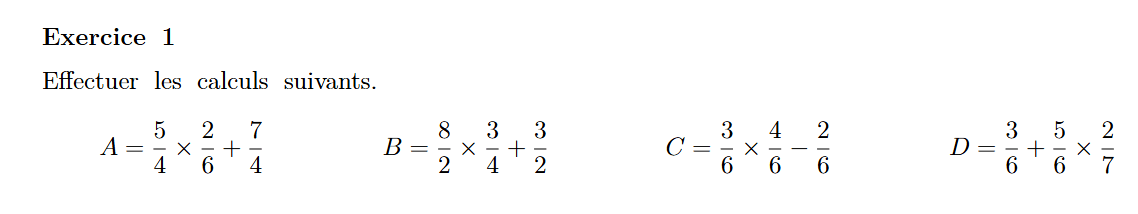
(sans calculatrice)
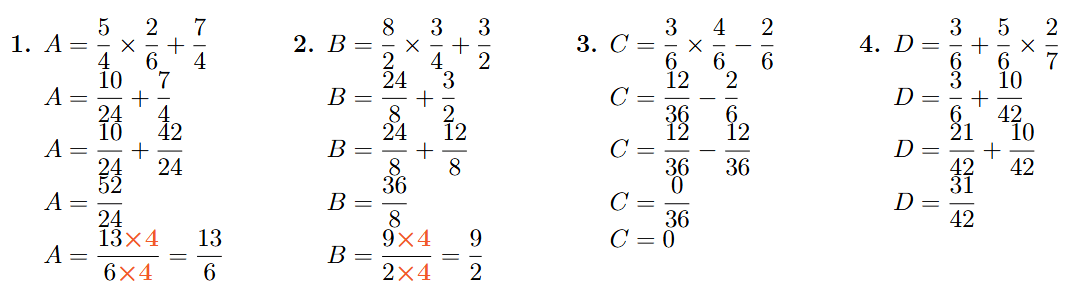
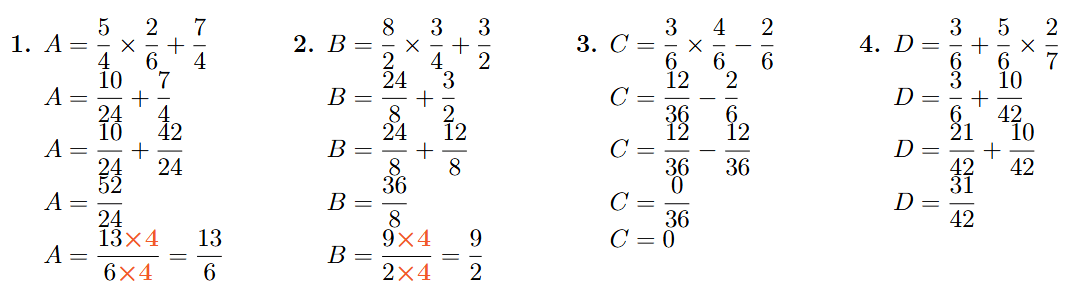
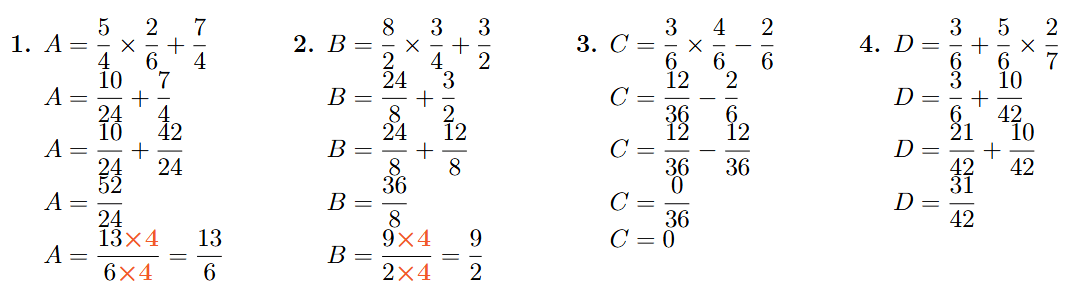
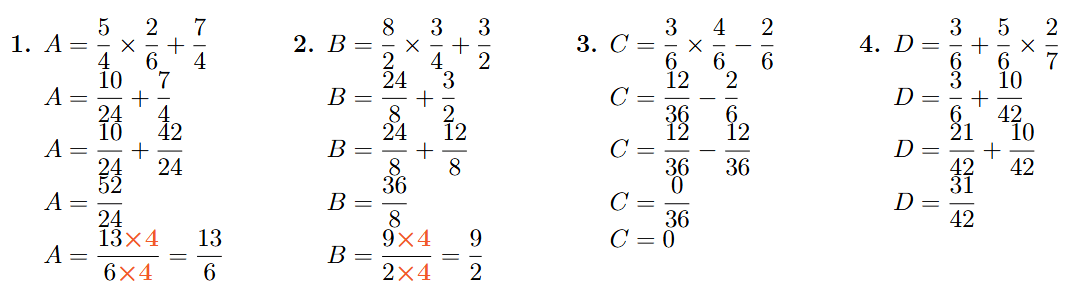
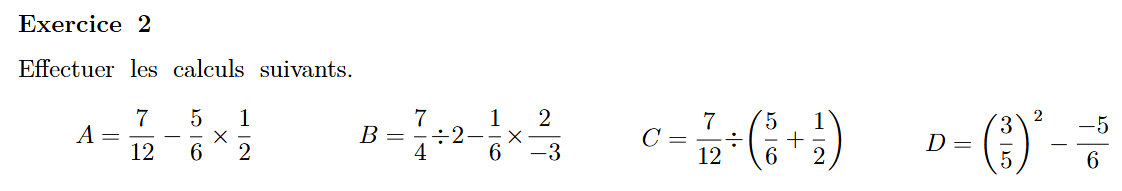
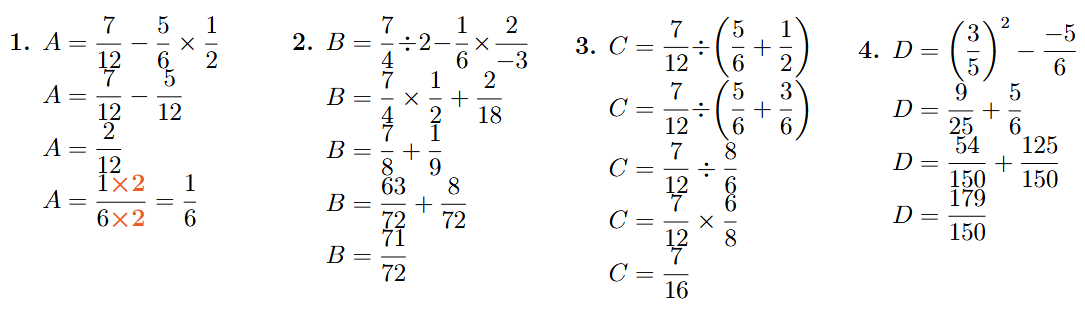
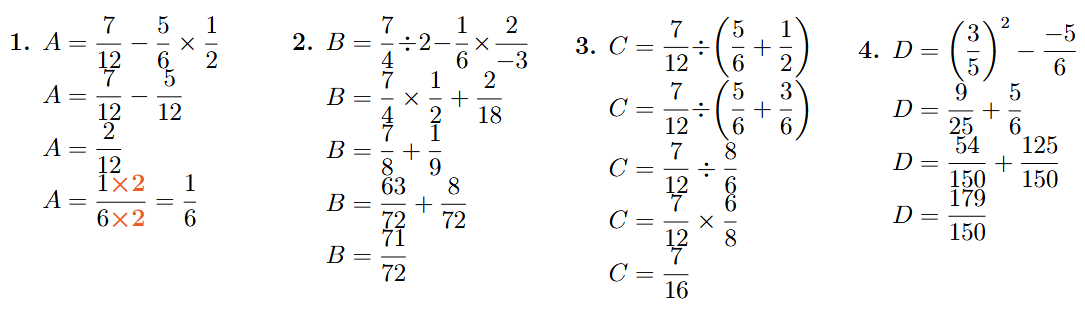
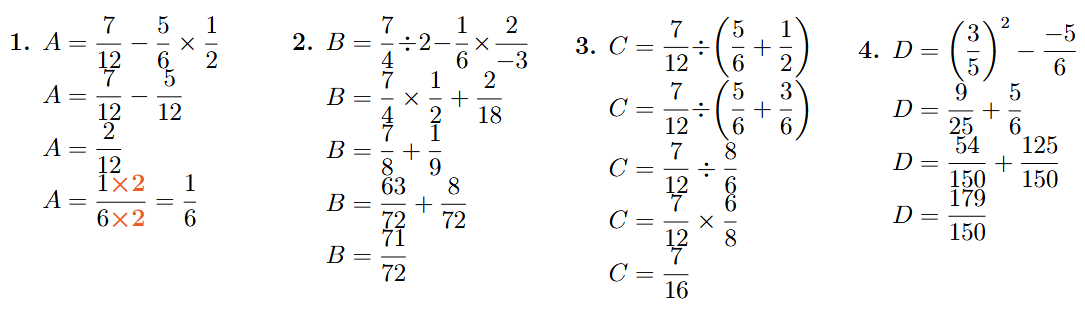
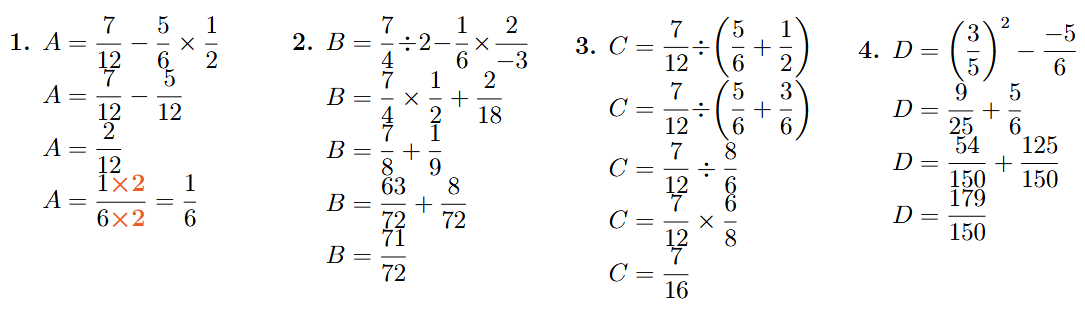





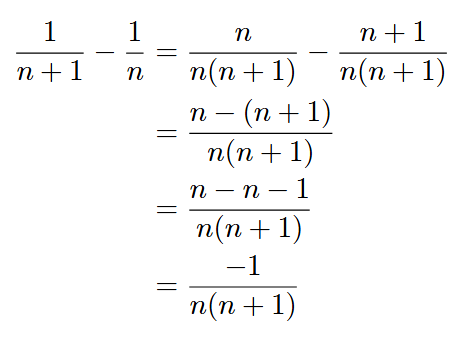
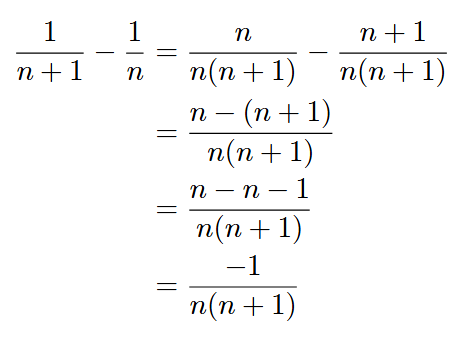


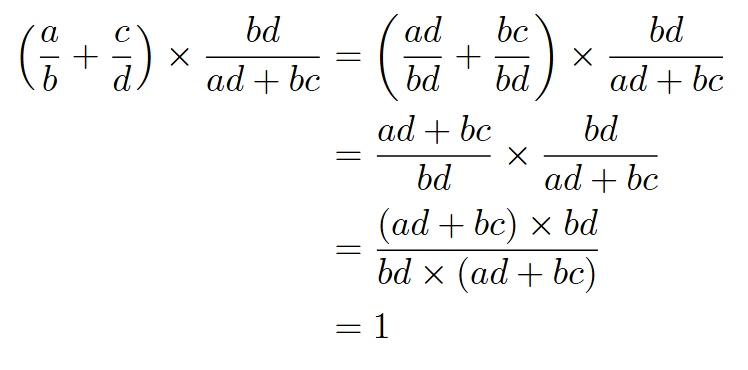
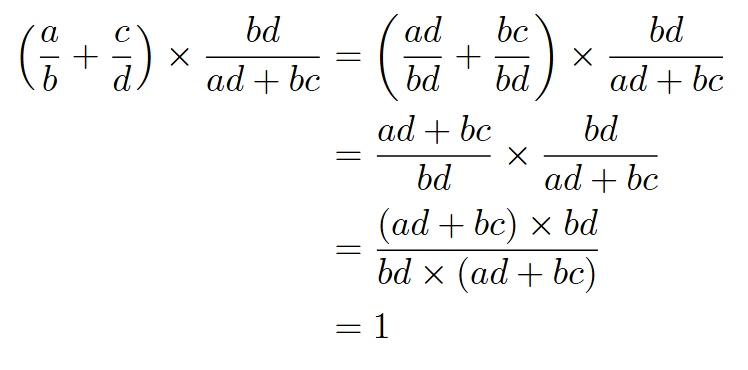









1.
3.
2.
5.
4.
9.



La première puissance est \(2^0\) ; la deuxième est \(2^1\) et ainsi de suite. La cinquième puissance de 2 est donc \(2^4=16\).
\(2^6=64\) et \(2^7=128\) donc 128 est la plus petite puissance de 2 supérieure ou égale à 100 .

\(2^9=512\) et \(2^{10}=1024\) donc 512 est la plus grande puissance de 2 inférieure ou égale à 1000 .

2.a La cinquième puissance de 3 est \(3^4=81\).
2.b \(3^4=81\) et \(3^5=243\) donc 243 est la plus petite puissance de 3 supérieure ou égale à 100 .
2.c \(3^6=729\) et \(3^7=2187\) donc 729 est la plus grande puissance de 3 inférieure ou égale à 1000 .

Programmation de l'algorithme en Python :
- Sur calculatrice (Numworks...)
Programmation en Python sur Calculatrice Numworks






La dernière valeur calculée par l'algorithme est 14.

Changer 10 000 en 50 000 et
print(n-1) à la place de print(n)

















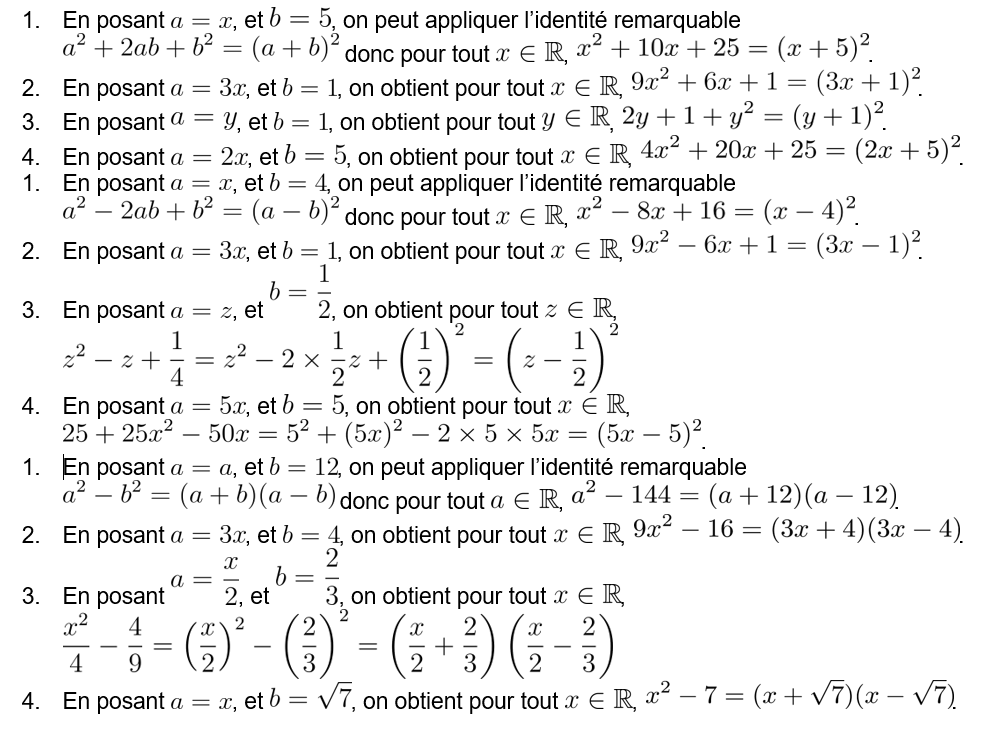


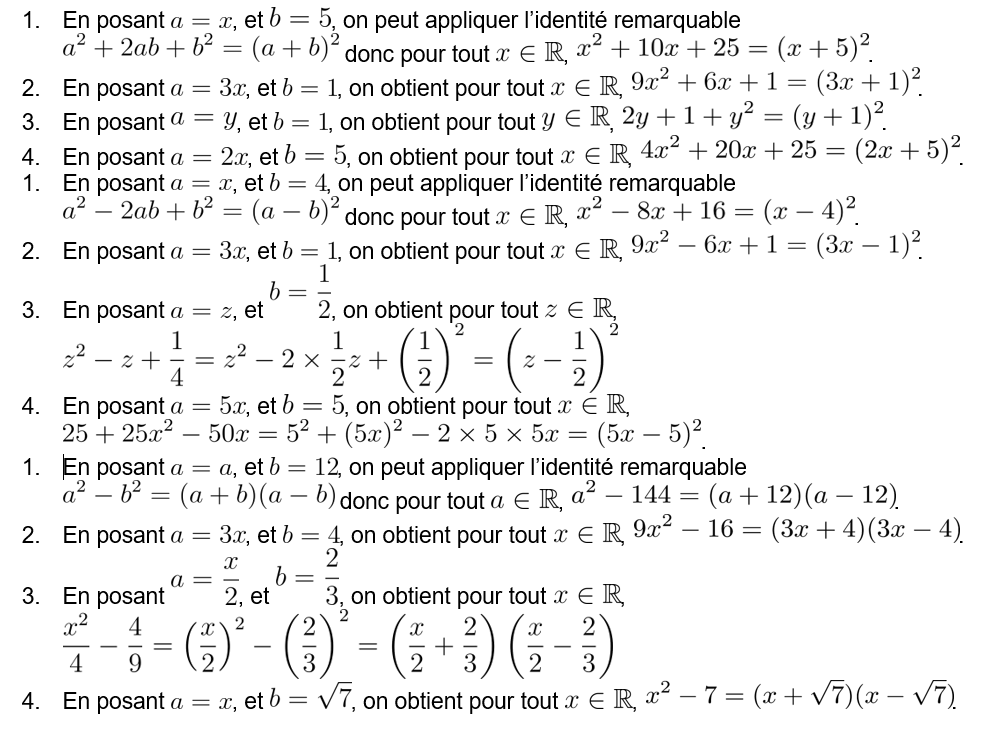


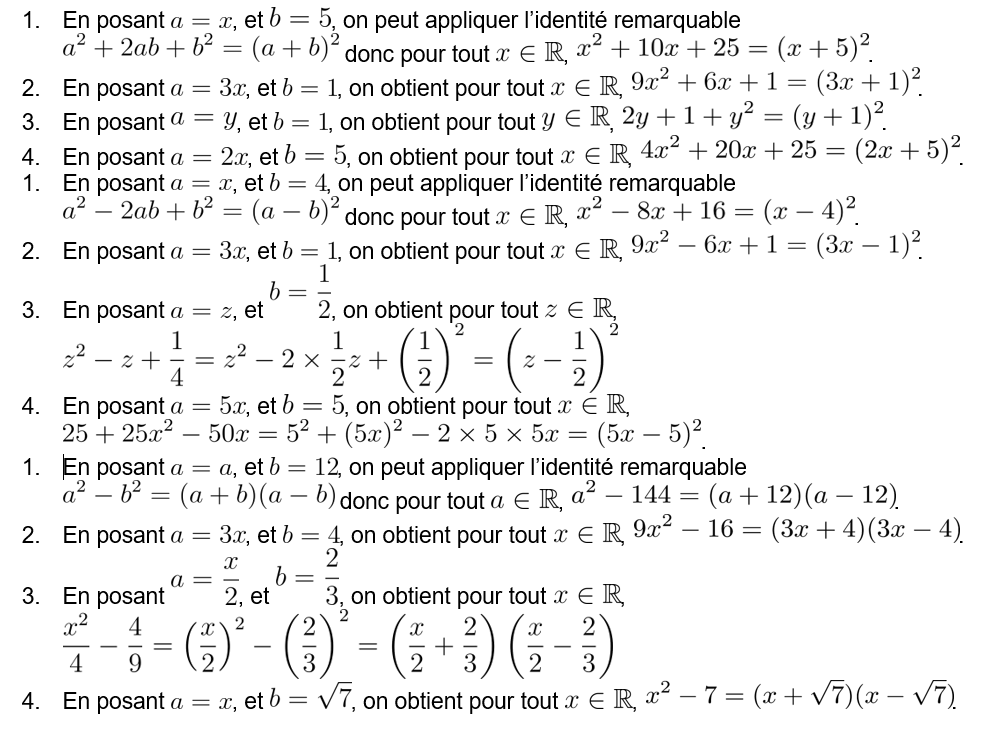
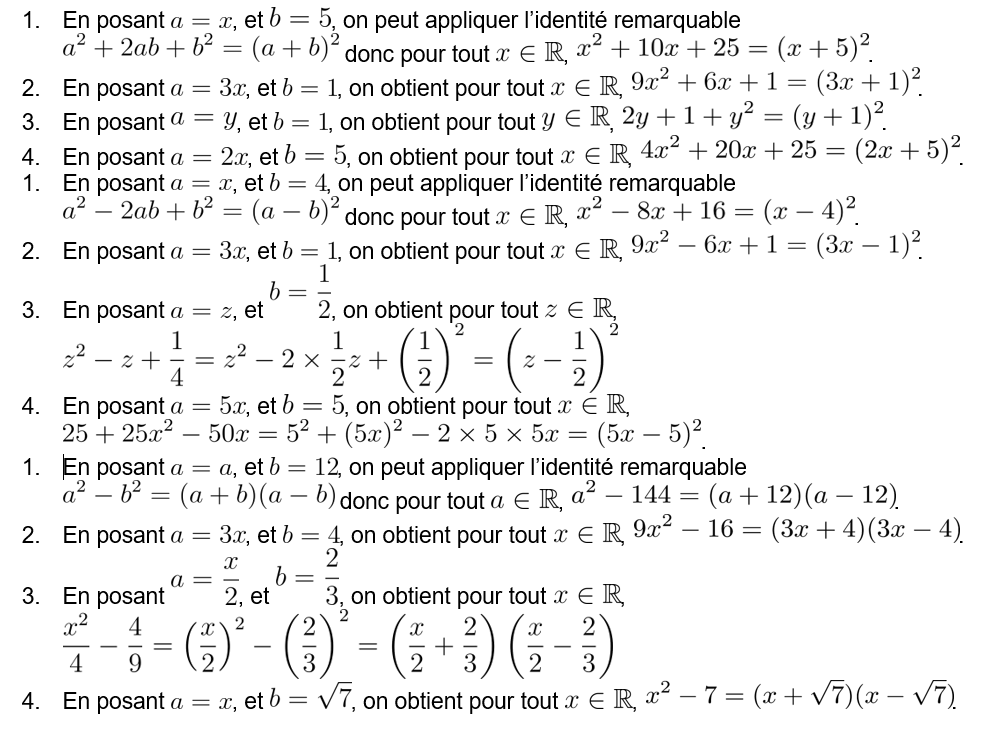





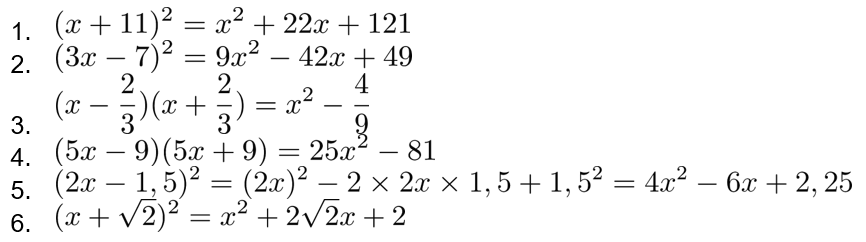


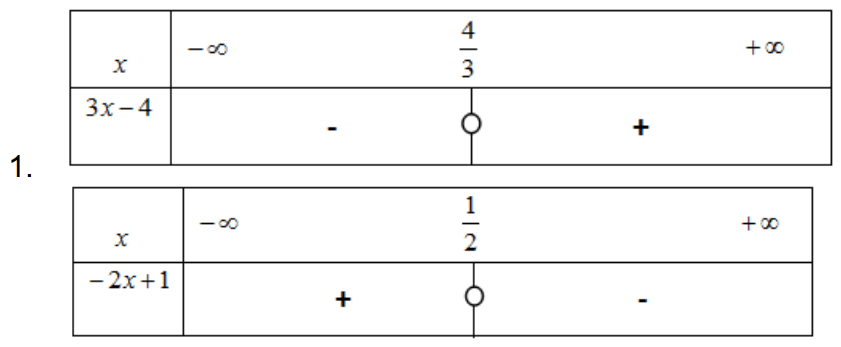
Exercice : Dresser le tableau de signes de l'expression \(3x-6\).
On résout l'inéquation \(3x-6\geqslant 0\).
l'expression \(3x-6\) est positive
lorsque \(x\) est supérieur ou égal à 2
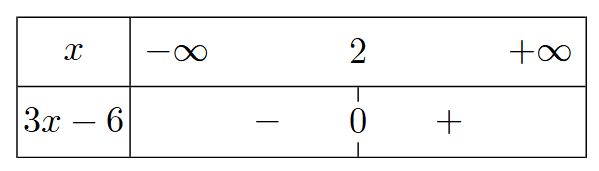
Exercice : Dresser le tableau de signes de l'expression \(-2x+5\).
On résout l'inéquation \(-2x+5\geqslant 0\).
l'expression \(-2x+5\) est positive
lorsque \(x\) est inférieur ou égal à 2,5
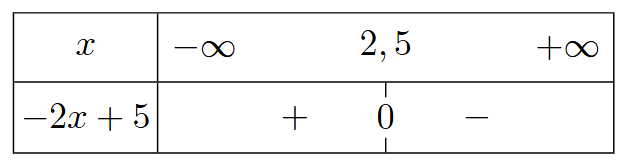

Ensemble des solutions de l'équation

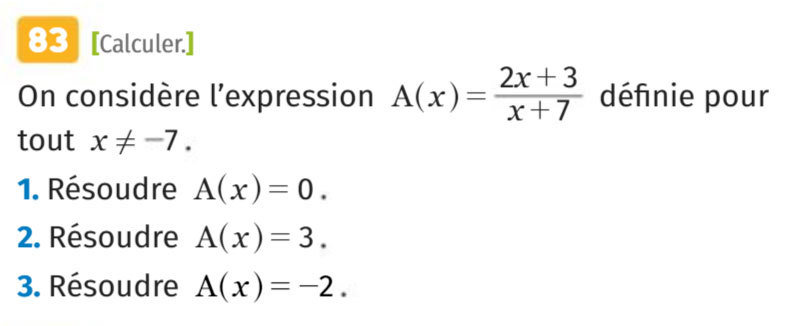






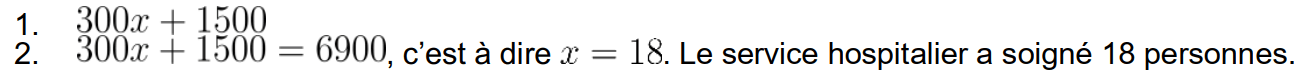
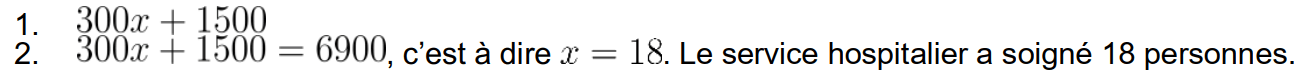















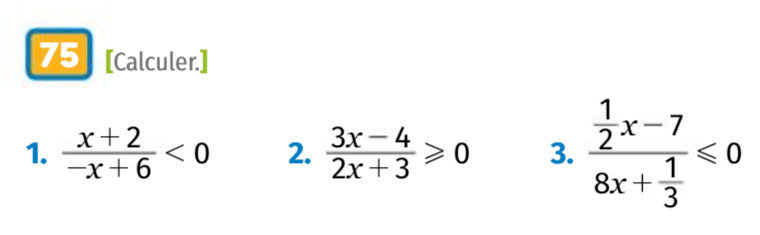
Calcul littéral : Exercices
By Jean-Marc Kraëber
Calcul littéral : Exercices
Seconde 2019
- 2,114



