Probabilités conditionnelles
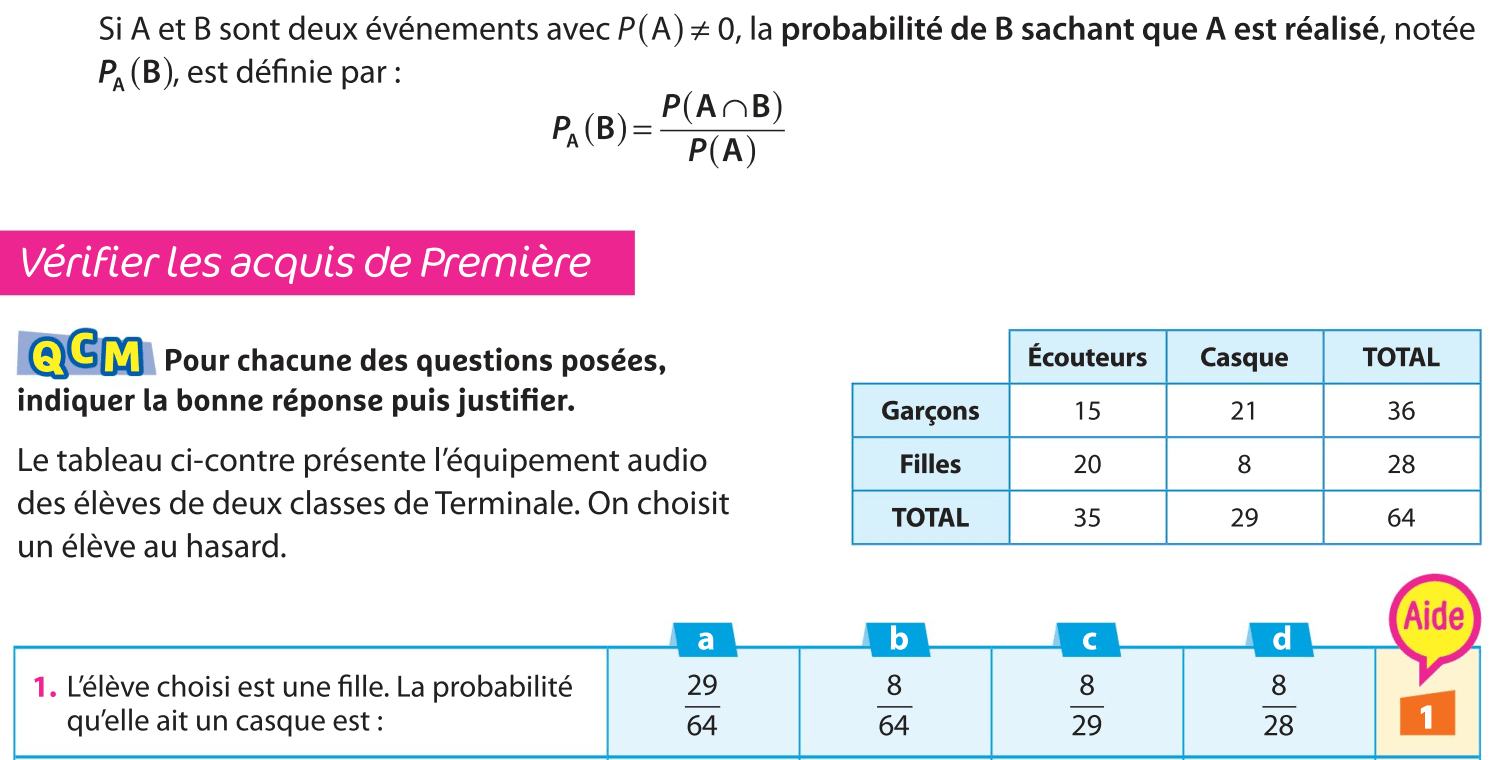




Act 1 p 120


0,7
0,4
0,8

A retenir :
En divisant par \(P(A)\), on retrouve la formule des probabilités conditionnelles :



0,7
0,4
0,8
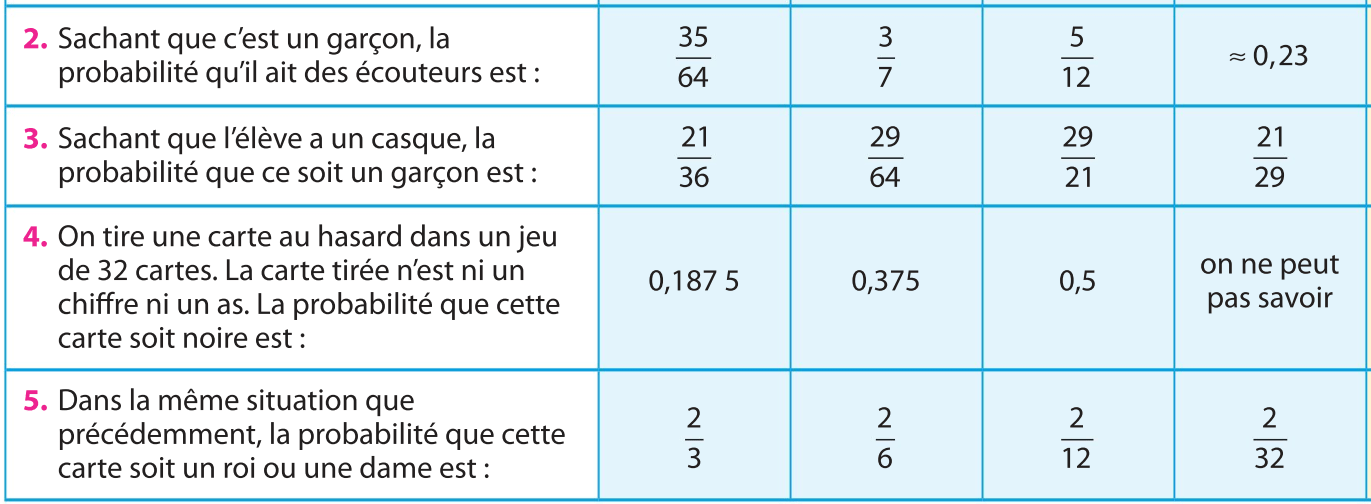
Act 2 p 120


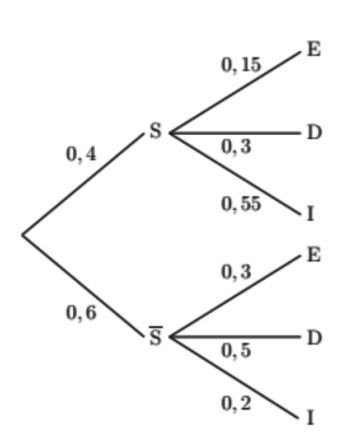
T ∩ M : « l’élève utilise le téléchargement et lit les vidéos sur son smartphone »
S ∩ M : « l’élève utilise le streaming et lit les vidéos sur son smartphone »


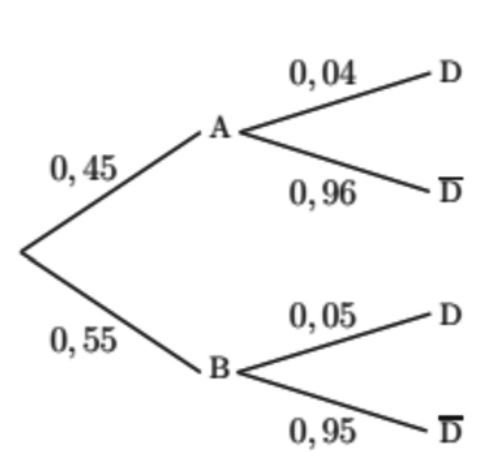
D'après la formule des probabilités totales :



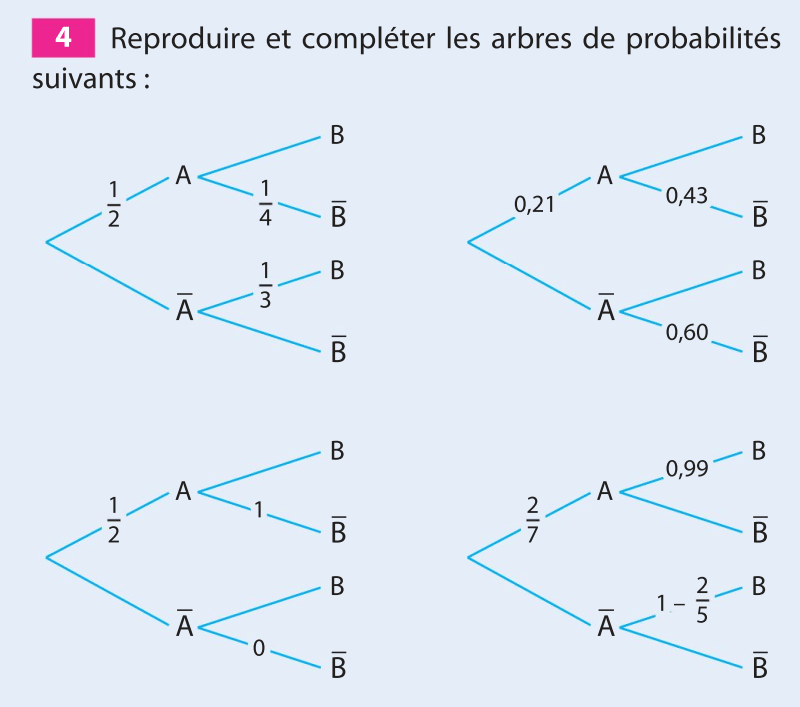
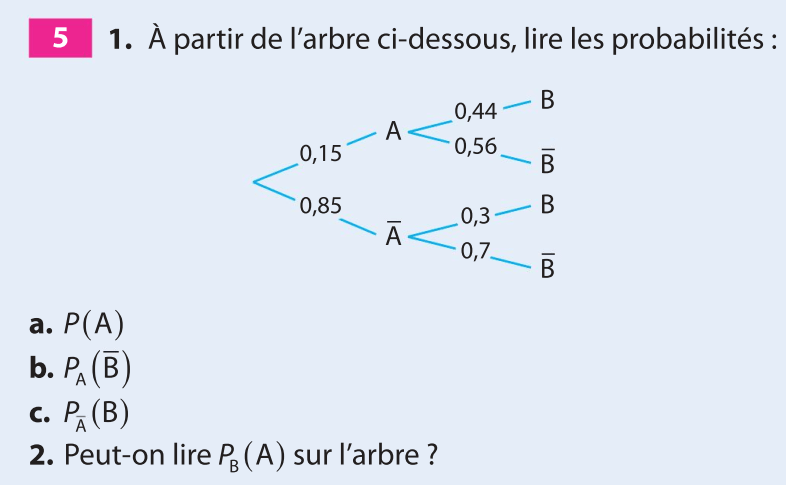
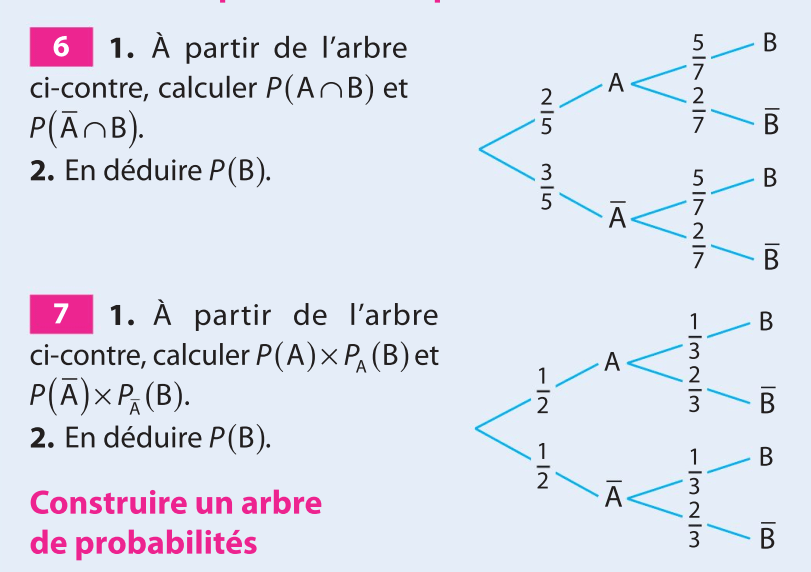
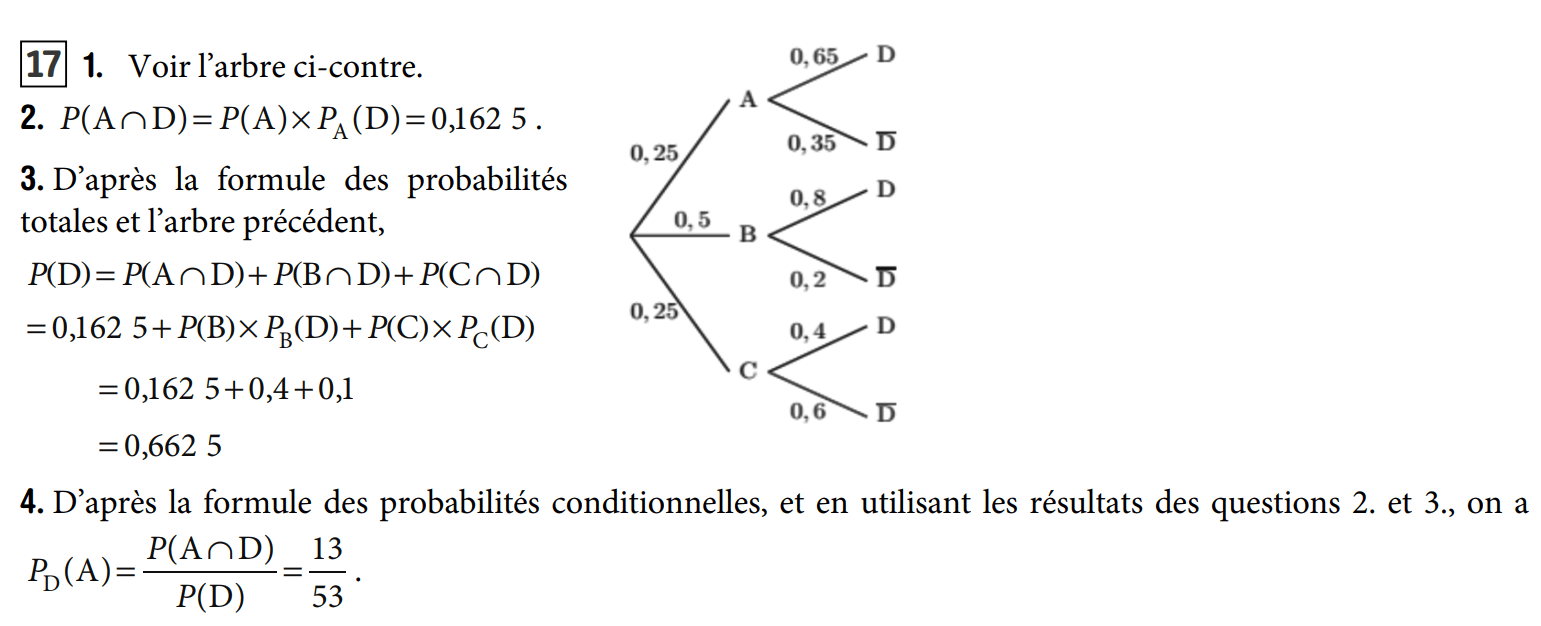
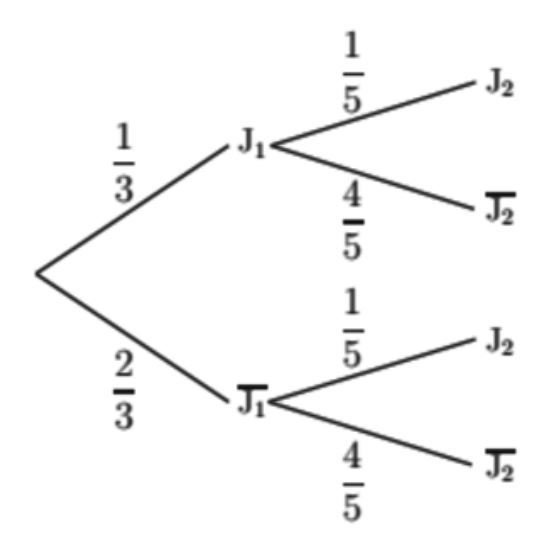
1.
2. D'après la formule des probabilités totales on a :


1.
2. D'après la formule des probabilités totales on a :

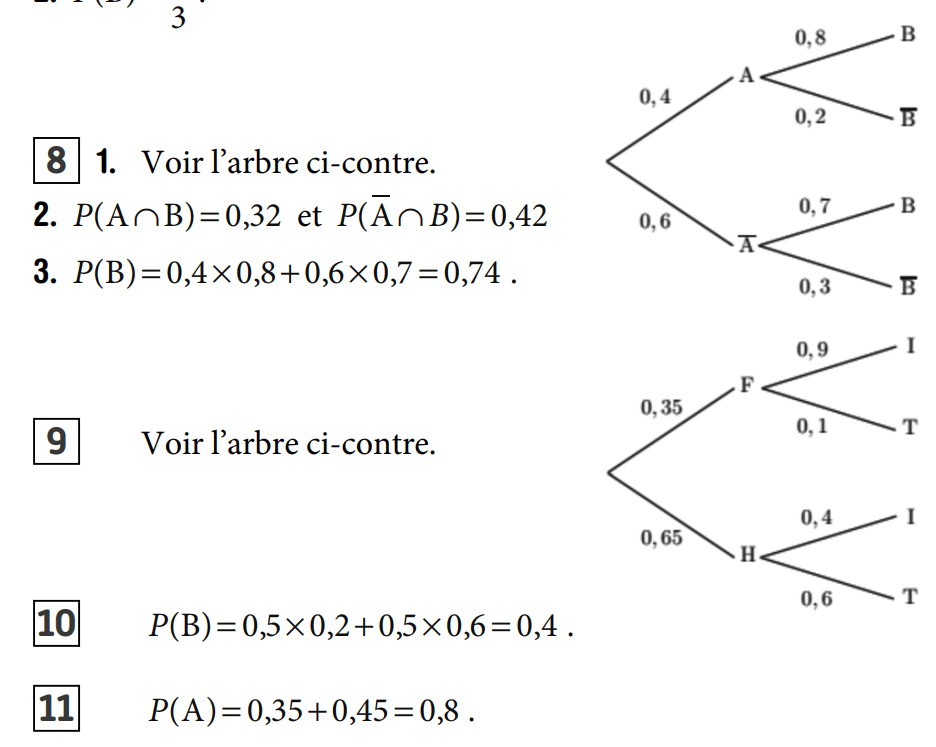

2.
3. D'après la formule des probabilités totales on a :


On note F : "l'employée est une femme".
On note H : "l'employé est un homme".
On note I : "l'employé(e) est un(e) ingénieur(e)".
On note T : "l'employé(e) est un(e) technicien(ne)".




On note G : "le licencié est un garçon".
On note M : "le licencié est majeur".
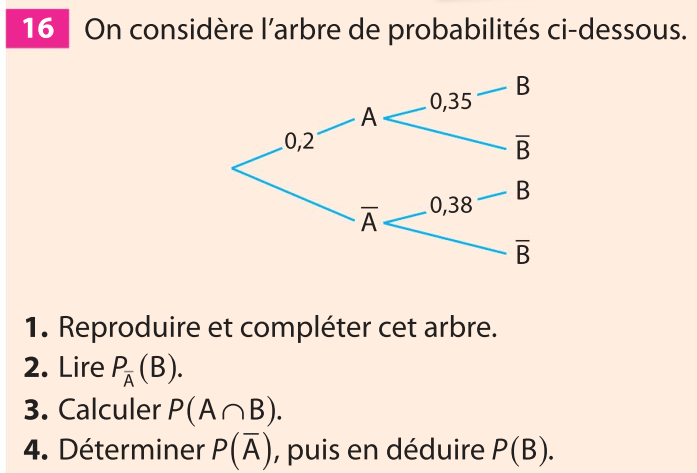





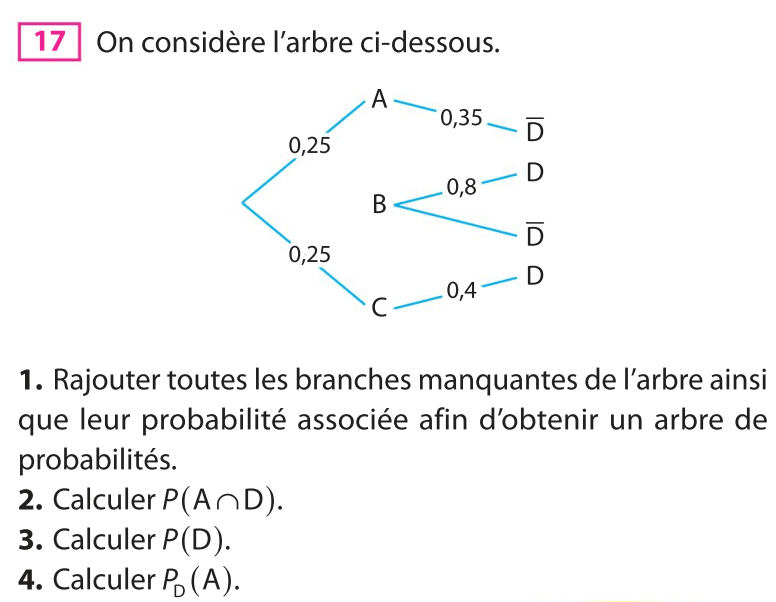







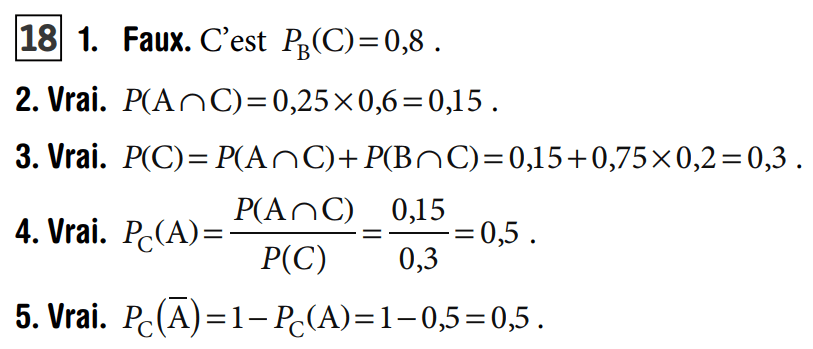
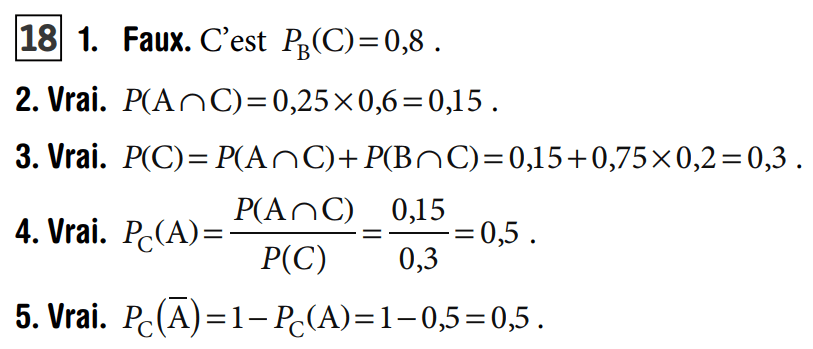
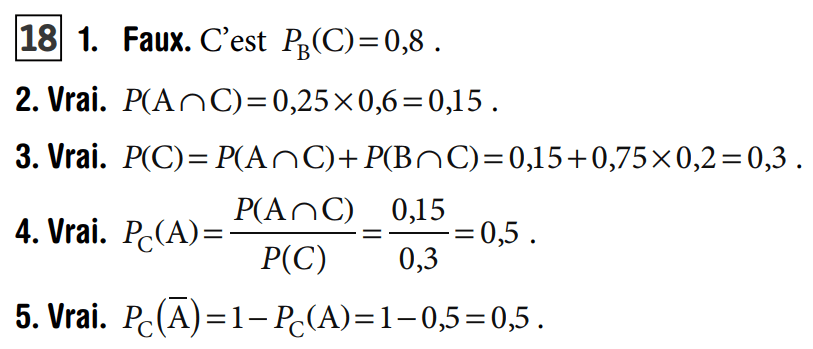
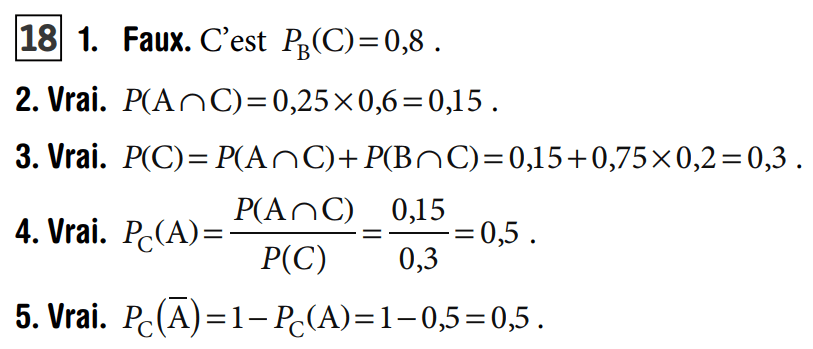
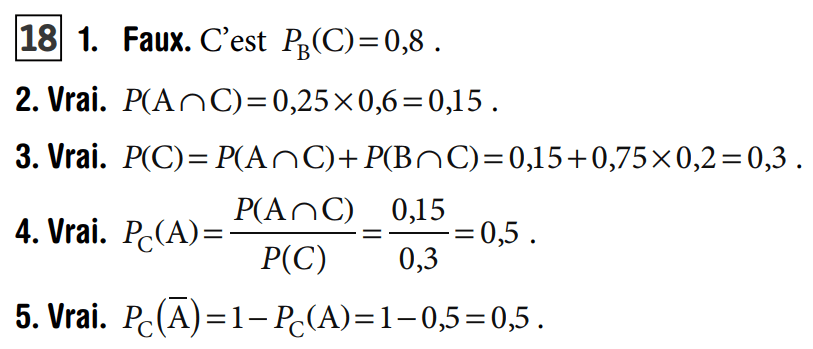







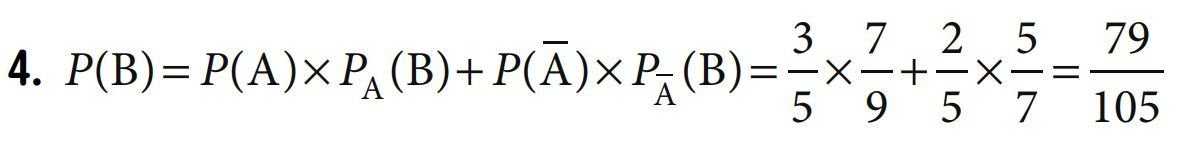






1. Faux

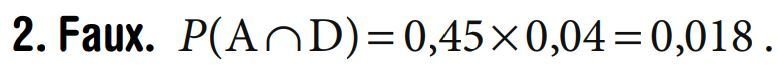


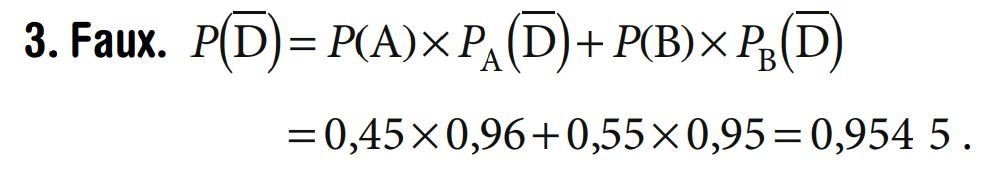

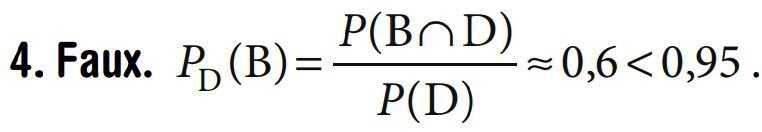

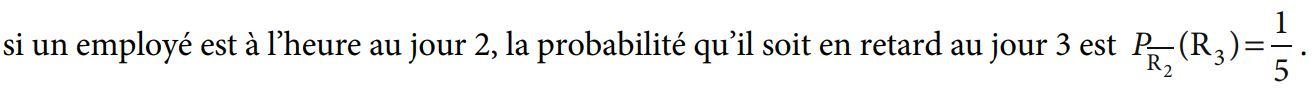

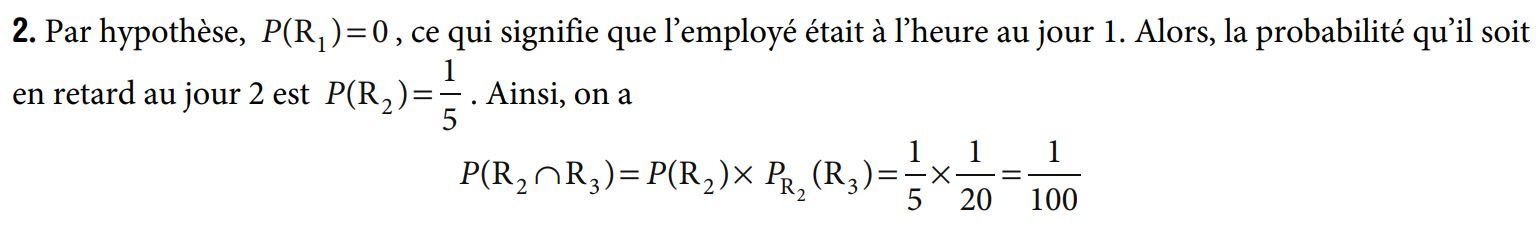
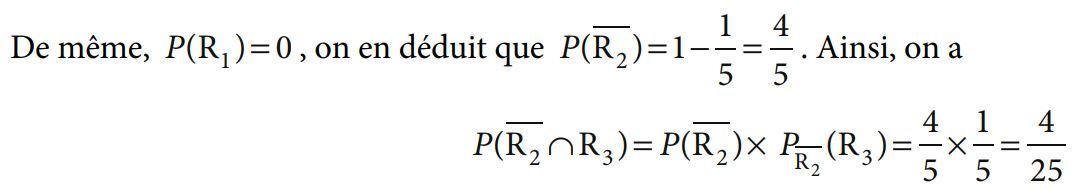



Indépendance de deux événements :





Réussir le premier et le deuxième service sont deux événements indépendants.



ou Réussir au moins un service est l'événement contraire de rater les deux :





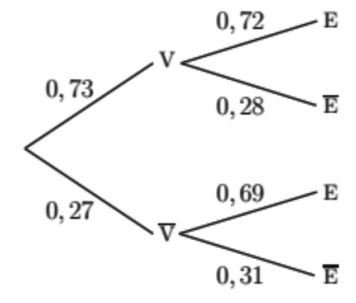
1. Les événements A et B ne sont pas indépendants mais incompatibles :
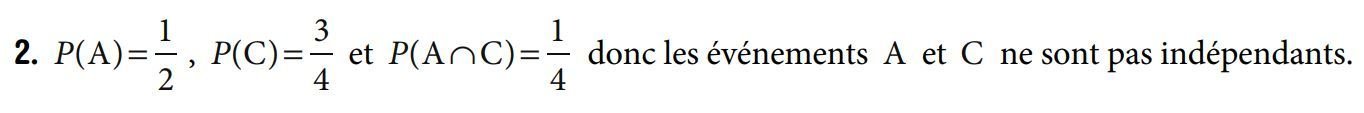

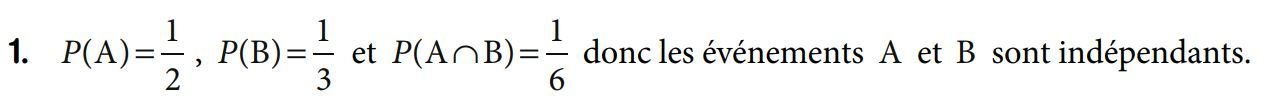

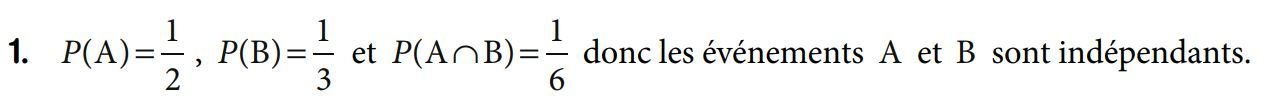



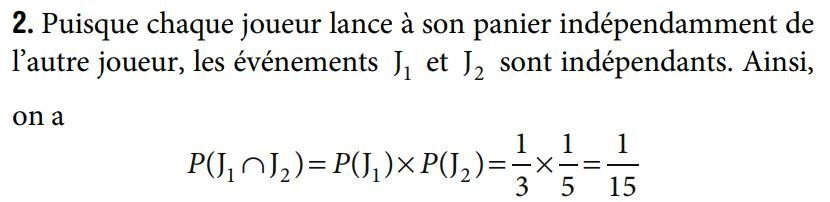





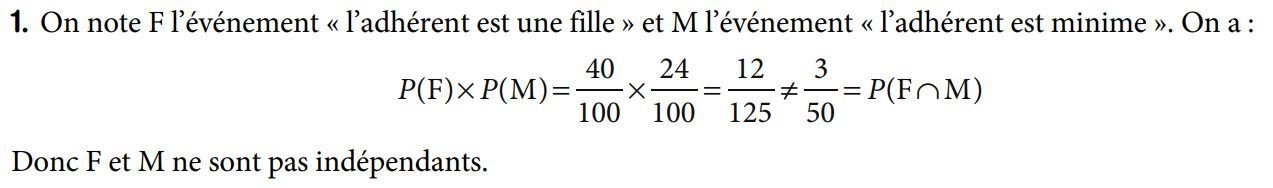

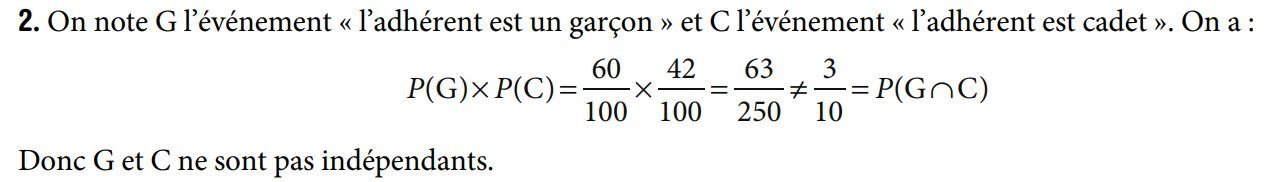



















TSTMG : Probabilités conditionnelles
By Jean-Marc Kraëber
TSTMG : Probabilités conditionnelles
Lycée Saint-Exupéry - La Rochelle
- 1,870



