

Elle est confondue avec d.
Faux : Soit a, l'abscisse du point A et f, la fonction représentée par C.
Le coefficient directeur de T est \(f'(a)\), le nombre dérivé de f en a et non \(f(a)\), l'ordonnée du point A.
Variation instantanée - Nombre dérivé

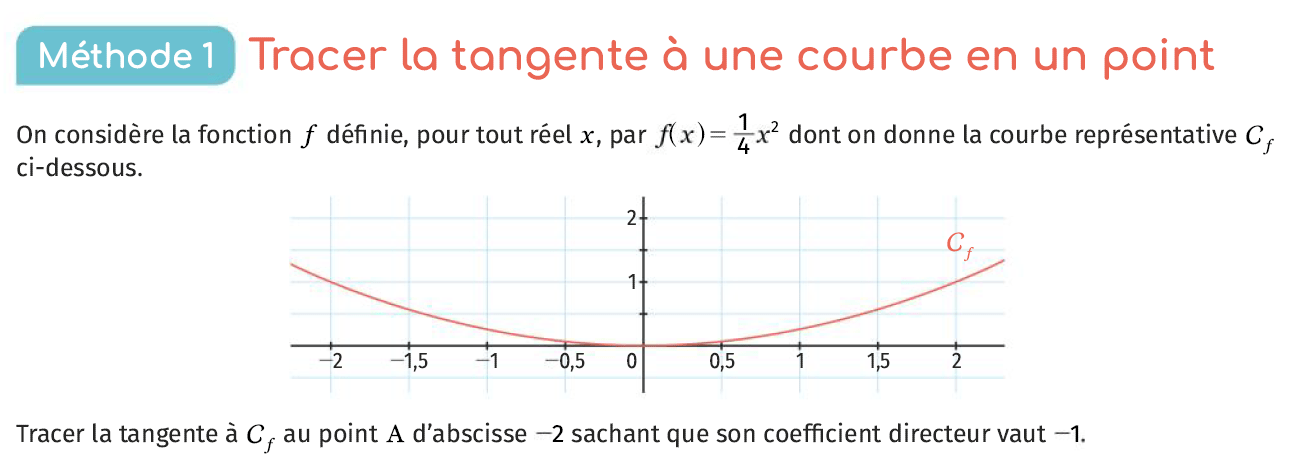
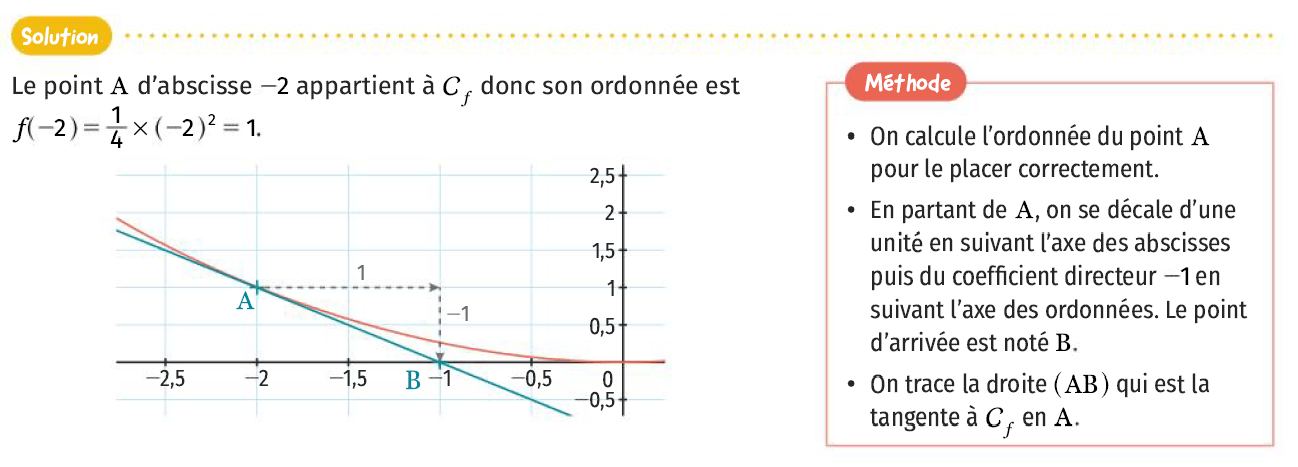
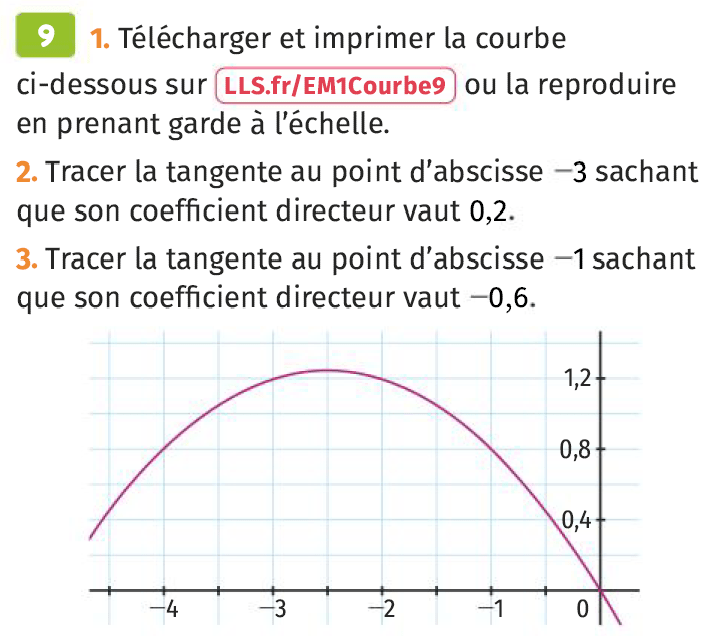

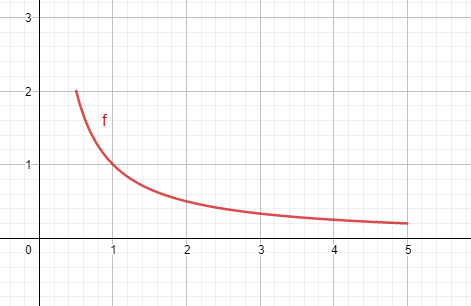

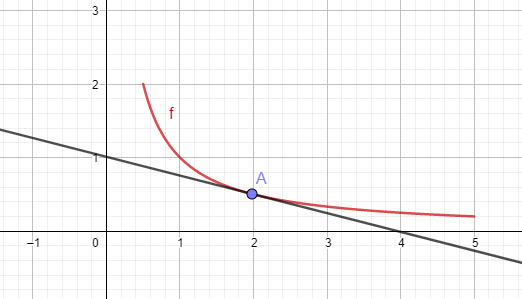
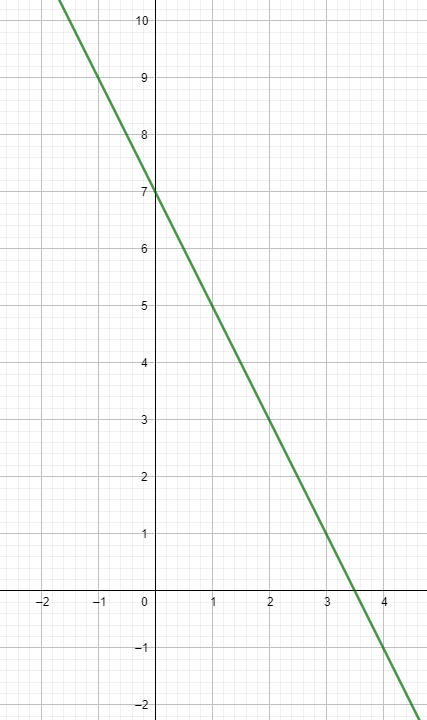
Le coefficient directeur est \(-0,25=-\dfrac{1}{4}\) ce qui signifie que lorsque l’on se déplace d’une unité vers la droite sur la tangente, l’ordonnée diminue de \(0,25\). On obtient ainsi la tangente suivante, passant par les points de coordonnées \((0\,;1)\) et \((4\,;0)\).
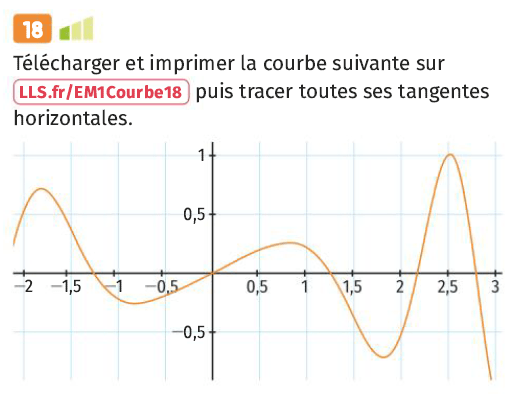
Si la tangente au point d’abscisse \(a\) est horizontale, alors son coefficient directeur vaut \(0\), donc \(f'(a)=0\).


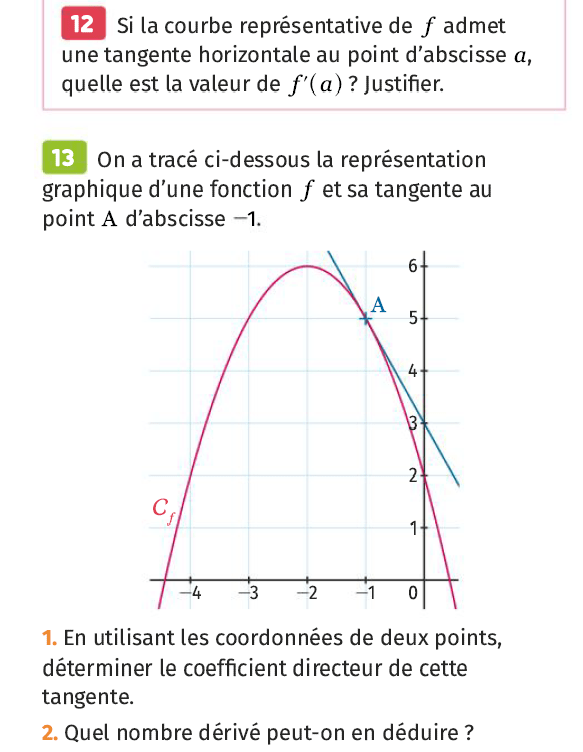
1) La tangente en \(A\) passe par les points \(A(-1\,;5)\) et \(B(0\,;3)\). Ainsi, le coefficient directeur de la tangente est \(\dfrac{y_B-y_A}{x_B-x_A}=\dfrac{3-5}{0 - (-1)}=-2\).
2) On en déduit que \(f'(-1)=-2\).

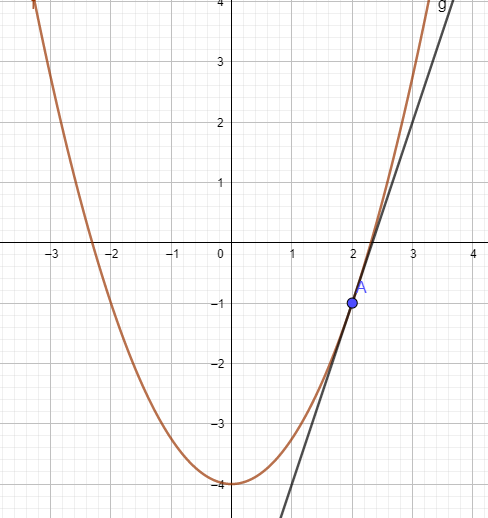
On commence par placer le point \(A(2\,;-1)\) par lequel la courbe doit passer. On trace également la droite passant par A et de coefficient directeur 3 qui devra être la tangente à la courbe au point A. On trace enfin une courbe possible. On obtient par exemple la courbe ci-dessous.
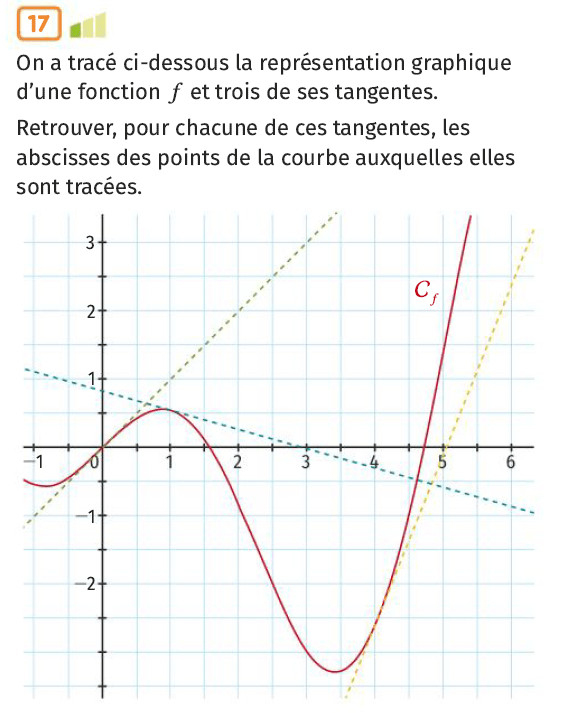
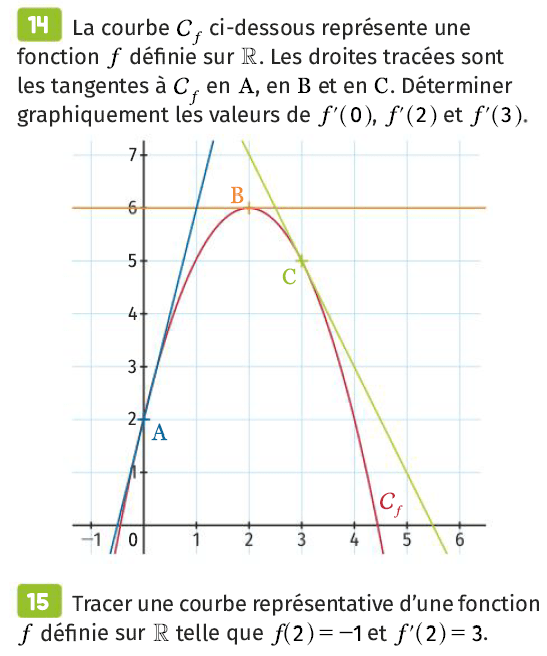
La droite verte est la tangente à la courbe représentative de \(f\) au point d’abscisse 0.
La droite bleue est la tangente à la courbe représentative de \(f\) au point d’abscisse 1.
La droite jaune est la tangente à la courbe représentative de \(f\) au point d’abscisse 4.

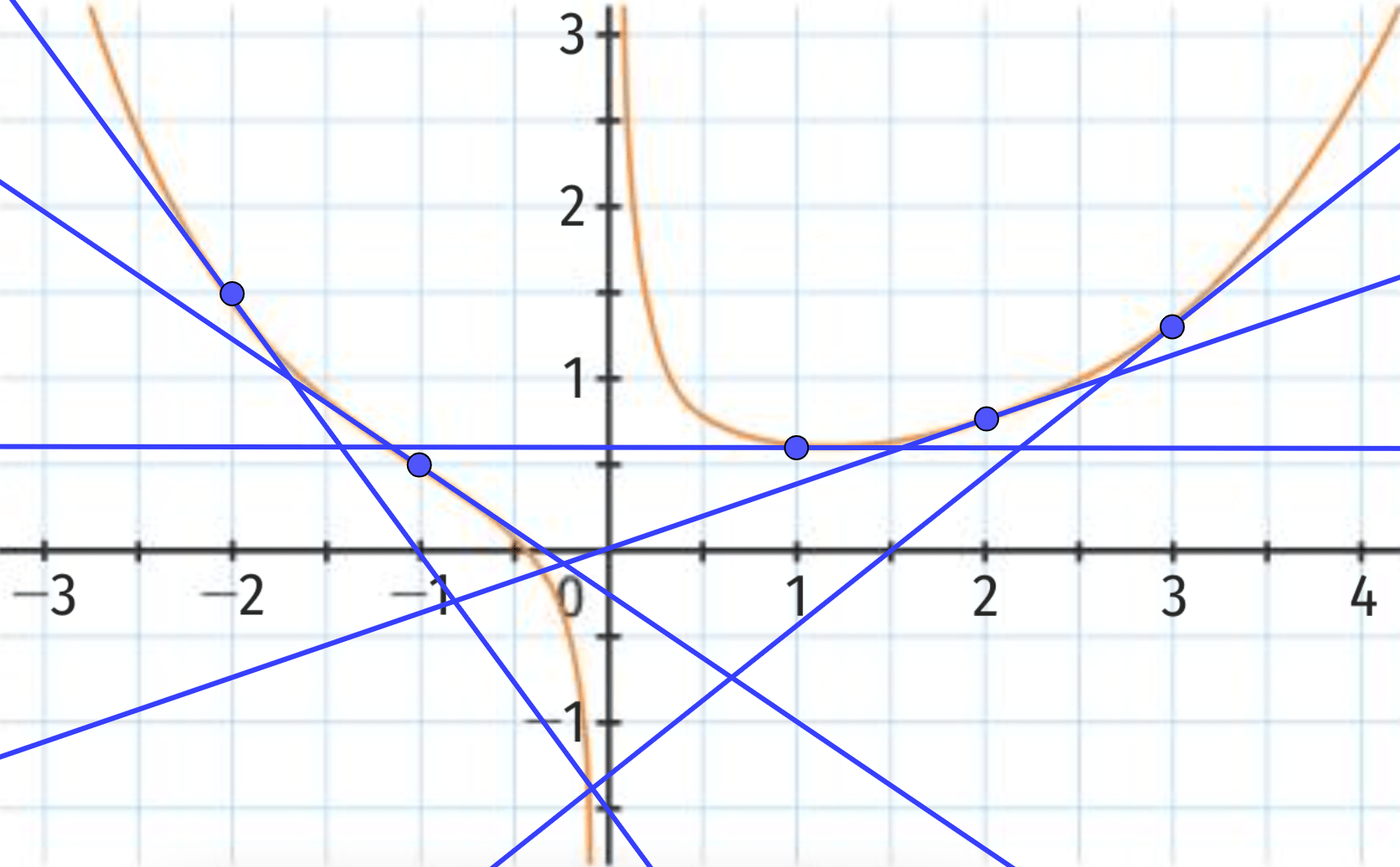




















b. La tangente à la courbe de \( f \) au point d’abscisse \(3\) est en fait confondue avec la courbe représentative de \(f\) elle-même.
c. La valeur de \( f'(3) \) est le coefficient directeur de la tangente au point d'abscisse 3 donc, d’après la question précédente, le coefficient directeur de la droite représentant f, qui vaut \(-2\).
d. Au point d’abscisse \(-4\), la tangente est à nouveau confondue avec la courbe de \(f\), et \(f'(-4) \) vaut donc encore \(-2\).



Variation instantanée
By Jean-Marc Kraëber
Variation instantanée
Lycée Saint-Exupery
- 1,704



