BreakID
now also for ASP
Jo Devriendt, Bart Bogaerts,
Maurice Bruynooghe, Marc Denecker
University of Leuven / Aalto University
State-of-the-art static symmetry breaking for SAT ported to ASP
Outline
- Static symmetry breaking in ASP
- Our contribution:
- Extending rule type support
- More stable graph coloring encoding
- Leveraging BreakID's improved symmetry breaking
- Experimental results
- Conclusion & Future work
Symmetry in ASP
- Defined for ground pogram with answer sets
- Permutation of literals is a symmetry if
- typically also
- Slows down search (exponentially)
- Often handled by posting
lex-leader symmetry breaking
formulas
\pi(\neg l)=\neg\pi(l)
\mathcal{P}
\pi(\mathcal{P})=\mathcal{P}
\pi
l
\mathcal{A}
\pi(\mathcal{A})=\mathcal{A}
Static symmetry breaking in ASP
ASP program in standard form (Lparse-Smodels)
Ground ASP program
Ground ASP program + symmetry breakers
Ground ASP program as a colored graph
Grounding
"Graphing"
Automorphism detection + symmetry breaking formula construction
"Graphing"
h_1\vee \ldots \vee h_l \leftarrow a_1 \wedge \ldots \wedge a_n \wedge \neg b_1 \wedge \ldots \wedge \neg b_m
Graph encoding of standard rule :
Graph encoding of literal :
l
r
"Graphing"
h \leftarrow g \leq \mathrm{sum}\{a_1=w_1, \ldots, a_n=w_n, \neg b_1=w_{n+1}, \ldots, \neg b_m=w_{n+m}\}
Graph encoding of integer :
Graph encoding of weight rule :
w
r
"Graphing"
- BreakID also supports
- Choice rule
- Minimize rule
- == Lparse-Smodels + Disjunctive rules
- (6 + #weights) colors
- (#heads + #bodies + #weights + #literals) nodes
- O( ) edges
\mathcal{P}
Difference with SBASS (alternative ASP symmetry breaker)
- support for Minimize and Weight rule
- undirected edges
"Graphing"
\mathcal{P}\colon
- SBASS detects no symmetry?
- BreakID detects interchangeability of {p,q}
0 \leq \#\{p\} \leq 1.
0\leq \#\{q\} \leq 1.
Hypothesis: Saucy only supports undirected edges
Symmetry breaking formulae
of BreakID
Motivating example for BreakID: pigeonhole problem
Only 2 more instances solved?
Let's try Shatter on the pigeonhole problem...
Only 2 more instances solved?
- Problem lies with generator symmetries Σ
- <Σ> is not completely broken by conjunction of sbf(σ), σ∈Σ
- For pigeonhole, there does exist some small Σ' for which sbf(σ), σ∈Σ' breaks <Σ> completely
In general, Σ lacks information on structure of group <Σ>
Symmetry breaking formula
BreakID tries to exploit symmetry group structure
- Detect row interchangeability symmetry subgroups
- Symmetry breaking based on stabilizer chain of symmetry group
- Small performance optimizations
Symmetry breaking formulae
-
Row interchangeability: common form of symmetry
- Stems from interchangeable objects
- Variables can be ordered as rows in matrix
- All permutations of rows are symmetries
- Can be broken completely by constructing symmetry breaking formula only for consecutive row swaps
- Assuming appropriate variable ordering
Symmetry breaking formulae
Detecting row interchangeability
| Occupies(p1,h1) | Occupies(p1,h2) | Occupies(p1,h3) |
| Occupies(p2,h1) | Occupies(p2,h2) | Occupies(p2,h3) |
| Occupies(p3,h1) | Occupies(p3,h2) | Occupies(p3,h3) |
| Occupies(p4,h1) | Occupies(p4,h2) | Occupies(p4,h3) |
Variable rows for 4 pigeons, 3 holes:
Symmetry due to interchangeable pigeons completely broken by
sbf(swap(p1,p2)) ∧ sbf(swap(p2,p3)) ∧ sbf(swap(p3,p4))
Detecting row interchangeability
- Input: CNF theory T, Σ detected by Saucy
- Output: variable matrix M such that rows are interchangeable and <M>⊆<Σ>
- extract σ1, σ2 ∈Σ that form 2 subsequent row swaps
- forms initial 3-rowed variable matrix M
- apply every σ∈Σ to all detected rows r∈M so far
- images σ(r) disjoint of M are candidates to extend M
- test if swap r ↔ σ(r) is a symmetry by syntactical check on T
- if success, extend M with σ(r)
- use Saucy to extend Σ with new symmetry generators by fixing all variable nodes with variable in M, first row excepted
Let's try BreakID on the pigeonhole problem,
while detecting row interchangeability
- Detects full pigeon subsymmetry and hole subsymmetry
- Poly performance
- 100+ holes are no problem
Symmetry breaking formulae
- If symmetry stabilizes literal , then
is a valid lex-leader symmetry breaking formula for symmetry group - BreakID maximizes the number of binary symmetry breaking clauses
- by adjusting variable order
\neg l \vee \pi(l)
\pi
l
Symmetry breaking formulae
BreakID derives binary symmetry breaking clauses
based on chains of stabilizer subgroups
Stabilizer chain symmetry breaking
\forall i\colon (\forall j < i \colon x_j \Leftrightarrow \sigma(x_j)) \Rightarrow \neg x_i \vee \sigma(x_i)
- Recall sbf(σ):
- for i=0:
-
Binary symmetry breaking clause
- x is stabilized by <Σ> iff σ(x)=x for all σ∈<Σ>
-
x' ∈ orbit(x) under <Σ> iff there exists σ∈<Σ> s.t. σ(x)=x'
- Given symmetry group <Σ> with smallest non-stabilized variable x, with x' ∈ orbit(x) under <Σ>,
is logical consequence of sbf(σ) for all σ∈<Σ>
- Moreover, all binary clauses in sbf(σ) for all σ∈<Σ> are derived this way [4]
\neg x_0 \vee \sigma(x_0)
\neg x \vee x'
Stabilizer chain symmetry breaking
- <Σ> has subgroups that have other smallest non-stabilized variables, depending on variable order
- Create stabilizer chain of <Σ> along variable ordering:
- next subgroup Gi is the stabilizer subgroup stabilizing the next non-stabilized variable in ordering
- Gi have different smallest non-stabilized variables x
- for each i: Orbit(x) under Gi leads to binary symmetry breaking clauses
- Derives all binary symmetry breaking clauses of <Σ> under variable ordering
<\Sigma> = G_0 \supset G_1 \supset \ldots \supset 1
Stabilizer chain symmetry breaking
| Occupies(p1,h1) | Occupies(p1,h2) | Occupies(p1,h3) |
| Occupies(p2,h1) | Occupies(p2,h2) | Occupies(p2,h3) |
| Occupies(p3,h1) | Occupies(p3,h2) | Occupies(p3,h3) |
| Occupies(p4,h1) | Occupies(p4,h2) | Occupies(p4,h3) |
Occupies(p1 ,h1) < Occupies(p2 ,h1) < Occupies(p3 ,h1) < Occupies(p4 ,h1) < ...
Stabilizer chain for pigeon symmetry consists of 4 subgroups
G0 permutes rows 1-2-3-4,
G1 permutes rows 2-3-4,
G2 swaps rows 3-4,
G3=1
Binary symmetry breaking clauses:
¬Occupies(p1 ,h1) v Occupies(p2 ,h1)
...
¬Occupies(p3 ,h1) v Occupies(p4 ,h1)
- More compact conversion of sbf to CNF [5]
- 3 clauses of size 3 instead of
4 clauses of sizes 3-4
- 3 clauses of size 3 instead of
- Limit the size of symmetry breaking formula to 50
- Limit symmetry detection time of Saucy
Symmetry breaking formulae
BreakID's small optimizations compared to Shatter / Sbass
Symmetry breaking in SAT competitions?
- BreakID overhead is low enough to be competitive, even on asymmetric instances
- Participated succesfully in SAT13, SAT15 competitions
- Experimental results on SAT14 instances
(Glucose as base solver)
Summary
- BreakID follows in Shatter's footsteps (after ~10 years!)
- Derive group structure information
- Row interchangeability detection
- Stabilizer chain based symmetry breaking
- Both are approximative algorithms
- Efficiency optimizations ensure competitiveness
Experimental comparison
of BreakID and SBASS
Experimental comparison
of BreakID and SBASS
Conclusion
- BreakID also works in an ASP setting
- Supports two extra rule types
- More robust due to undirected edges
- More efficient due to smarter symmetry breaking formulas
Future work?
- Symmetry detection on predicate level
- Paper presentation next friday ;)
-
Dynamic symmetry breaking
- Work underway, ready by SAT17 :)
Future of symmetry handling
ASP program in standard form (Lparse-Smodels)
Ground ASP program
Ground ASP program + symmetry breakers
Ground ASP program as a colored graph
Grounding
"Graphing"
Automorphism detection + symmetry breaking formula construction
Predicate level symmetry detection
Symmetry handling during search
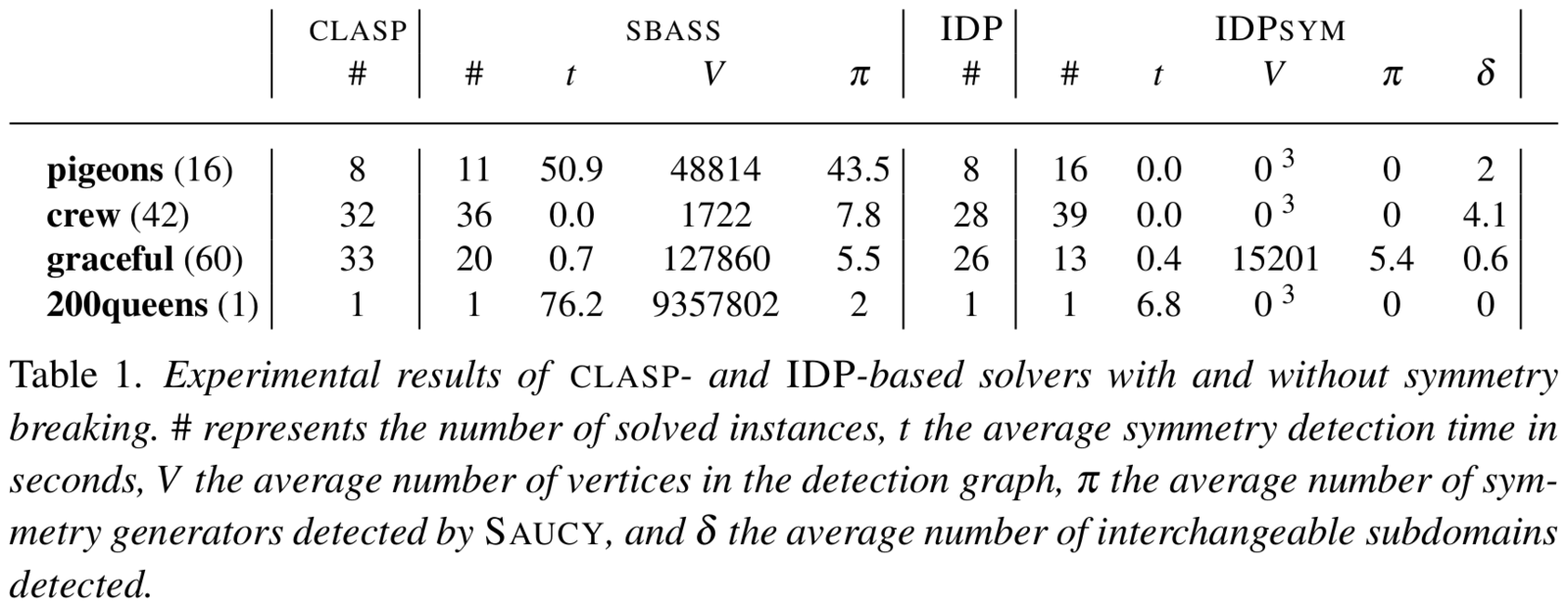
Experimental comparison
of IDP and SBASS
Thanks for your attention!
Questions?
[0] Improved Static Symmetry Breaking for SAT - 2016 - Devriendt et al.
[1] Symmetry and Satisfiability: An Update - 2010 - Katebi et al.
[2] Efficient Symmetry-Breaking for Boolean Satisfiability - 2006 - Aloul et al.
[3] On the importance of row symmetry - 2014 - Devriendt et al.
[4] Automatic generation of constraints for partial symmetry breaking - 2011 - Jefferson & Petrie
[5] Symmetry and satisfiability - 2009 - Sakallah
[6] On Local Domain Symmetry for Model Expansion - 2016 - Devriendt et al. (presentation Friday)
BreakID-ASP
By Jo Devriendt
BreakID-ASP
SAT16
