Constraint Reasoning,
Pseudo-Boolean Style
Jo Devriendt
KU Leuven
Acknowledgment:
MIAO group headed by Jakob Nordström
Lund University, Sweden
University of Copenhagen, Denmark
slides @ slides.com/jod/kaho
Constraint Reasoning,
Pseudo-Boolean Style
PB solvers
-
Input: 0-1 IL program
(integer coefficients and rhs) -
Output: either
- (optimal) solution
- proof that no solution exists
- generalizes
Boolean satisfiability (SAT) solving
Constraint Reasoning,
Pseudo-Boolean Style
Talk outline
- PB constraint learning
- intermezzo: proof complexity I
- PB cut generation
- intermezzo: proof complexity II
- PB lower bound derivation
- Outro: selected experimental results
PB constraint learning
(example-driven)
- Input: 0-1 IL program (integer coefficients and rhs)
-
Output: either
- (optimal) solution
- proof that no solution exists
-
Search state:
- set of constraints φ
- partial assignment α
-
Initial state:
- φ = input
- α = {}
-
Depth-first search loop
- "learning" an implied constraint from failure
PB constraint learning
Unit propagation
PB constraint learning
- Under α, if a constraint c ∈ φ would be falsified by assuming x=0 (resp. x=1), extend α with x=1 (resp. x=0)
- Propagate until fixpoint
Unit propagation
Conflict?
- Conflict: some c ∈ φ falsified by α
PB constraint learning
Unit propagation
Conflict?
Decide unassigned variable
no
- Only if unit propagation did not lead to a conflict
- If no unassigned variable left, return solution
- Resume unit propagation
PB constraint learning
Unit propagation
Conflict?
Decide unassigned variable
no
- Only if unit propagation did not lead to a conflict
- If no unassigned variable left, return solution
- Resume unit propagation
PB constraint learning
Unit propagation
Conflict?
Decide unassigned variable
no
PB constraint learning
Unit propagation
Conflict?
Decide unassigned variable
no
PB constraint learning
Unit propagation
Conflict?
Decide unassigned variable
no
PB constraint learning
Unit propagation
Conflict?
Decide unassigned variable
no
PB constraint learning
Unit propagation
Conflict?
Decide unassigned variable
no
PB constraint learning
Unit propagation
Conflict?
Decide unassigned variable
no
PB constraint learning
Unit propagation
Conflict?
Decide unassigned variable
no
- Conflict: some c ∈ φ falsified by α
PB constraint learning
Unit propagation
Conflict?
Learn constraint
Decide unassigned variable
yes
no
- From falsified constraint and reasons, construct learned constraint
- implied by φ, should prevent conflict
- Add learned constraint to φ
- → learned constraint database
PB constraint learning
Unit propagation
Conflict?
Learn constraint
Decide unassigned variable
yes
no
- From falsified constraint and reasons, construct learned constraint
- implied by φ, should prevent conflict
- Add learned constraint to φ
- → learned constraint database
PB constraint learning
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
- Backtrack based on learned constraint
- Resume unit propagation
PB constraint learning
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
- Backtrack based on learned constraint
- Resume unit propagation
PB constraint learning
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
PB constraint learning
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
PB constraint learning
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
PB constraint learning
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
PB constraint learning
PB constraint learning
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
PB constraint learning
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
PB constraint learning
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
PB constraint learning
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
Unsatisfiable!
PB constraint learning
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
- Learning constraints pushes search forward
- Thousands of conflicts per second
- Originates from Boolean satisfiability (SAT) [MS96,BS97,MMZZM01]
- Generalized to pseudo-Boolean (PB) solving [CK05,SS06,LP10,EN18]
- many variations possible
here be dragons
PB constraint learning
Proof complexity I
- Study of proof systems
(== syntactic derivation rules == operations on the dual) - Proof: syntactic derivation of new formulas leading to inconsistency
- Given an unsatisfiable formula
(== program == set of constraints)
how to derive an inconsistency? - What are the lower/upper bounds on proof length for certain formulas?
- What are the relations between proof systems?
Proof complexity I


Proof complexity I

Proof complexity I
In our example
- Multiplication and addition were sufficient
- We could also have used variable axioms
- Multiplication, addition, axioms: essentially positive linear combinations of the ILP and the 0-1 bound constraints

Farkas' lemma:
There exists a positive linear combination of constraints that is clearly inconsistent
iff
The ILP is rationally infeasible

Another look at our example...
- It's rationally infeasible!
- How does a PB constraint reasoning work if it is rationally feasible, but 0-1 infeasible (unsatisfiable)?
-
Still derive 0 ≥ 1
- From non-empty to empty polytope...
- Cut generation!
PB cut generation
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
PB cut generation
Rational solution:
x = y = 0.5
z = v = w = 1
but still unsatisfiable
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
PB cut generation
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
PB cut generation
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
PB cut generation
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
PB cut generation
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
PB cut generation
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
PB cut generation
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
PB cut generation
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
PB cut generation
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
PB cut generation
add variable axiom 1 ≥ v
divide by 2, round up rhs
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
PB cut generation
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
PB cut generation
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
PB cut generation
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
PB cut generation
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
PB cut generation
Unsatisfiable!
Proof complexity II
Fourth rule: division (with rounding)

Together: cutting planes proof system
Proof complexity II
cutting planes proof system
- Alternatives to Division rule:
- Saturation
- MIR inequality
- ?
- Implicationally complete
- Machine-verifiable
- Theoretical foundation
for PB solvers - Strictly stronger than
resolution proof system

Proof complexity II
Resolution:
- Propositional clauses
- A clause is a 0-1 IL constraint:
-
Resolution rule
- In 0-1 ILP formalism
Proof complexity II
- Simple!
- Implicationally complete (for clauses)
- Resolution underpins SAT, CP, ASP, SMT, ...
- learn clauses instead of cutting planes
- Cutting planes polynomially simulates resolution
- For some important ILPs the shortest resolution proof is exponential and the shortest cutting planes proof is polynomial
- Exponential running time shows up in practice
Proof complexity II
- Theoretically much stronger proof systems exist
- Not known how to use them effectively in practice
- Weakest proof system (resolution) is most widely employed!
- Only recently, effective cutting planes (PB) solvers are being developed
- My work: Exact PB solver
gitlab.com/jod/exact
PB lower bound derivation
- Based on "core-guided optimization" from MaxSAT [FM06]
- core == learned constraint
- Central observation:
- given objective
- and constraint
- then A is a lower bound to O
- given objective
- Force solver to learn such constraints
PB lower bound derivation
Modified PB solver
-
Input:
- 0-1 IL program
- set of assumptions (== variable fixings) β
-
Output: either
- SAT: solution consistent with β
- UNSAT: learned constraint inconsistent with β (core)
Assume best case objective
PB call yields SAT?
Extract core
Reformulate objective,
increase lower bound
Optimal
no
yes
PB lower bound derivation
PB lower bound derivation
Simple solution:
x = y = z = v = w = 1
Optimal rational solution:
x = z = 0, y = v = 1/3, w = 2/3
Assume best case objective
PB call yields SAT?
Extract core
Reformulate objective,
increase lower bound
Optimal
no
yes
PB lower bound derivation
Assume best case objective
PB call yields SAT?
Extract core
Reformulate objective,
increase lower bound
Optimal
no
yes
PB lower bound derivation
Assume best case objective
PB call yields SAT?
Extract core
Reformulate objective,
increase lower bound
Optimal
no
yes
PB lower bound derivation
Assume best case objective
PB call yields SAT?
Extract core
Reformulate objective,
increase lower bound
Optimal
no
yes
PB lower bound derivation
Assume best case objective
PB call yields SAT?
Extract core
Reformulate objective,
increase lower bound
Optimal
no
yes
PB lower bound derivation
Assume best case objective
PB call yields SAT?
Extract core
Reformulate objective,
increase lower bound
Optimal
no
yes
PB lower bound derivation
Assume best case objective
PB call yields SAT?
Extract core
Reformulate objective,
increase lower bound
Optimal
no
yes
PB lower bound derivation
Assume best case objective
PB call yields SAT?
Extract core
Reformulate objective,
increase lower bound
Optimal
no
yes
PB lower bound derivation
Assume best case objective
PB call yields SAT?
Extract core
Reformulate objective,
increase lower bound
Optimal
no
yes
PB lower bound derivation
Assume best case objective
PB call yields SAT?
Extract core
Reformulate objective,
increase lower bound
Optimal
no
yes
PB lower bound derivation
Assume best case objective
PB call yields SAT?
Extract core
Reformulate objective,
increase lower bound
Optimal
no
yes
PB lower bound derivation
Assume best case objective
PB call yields SAT?
Extract core
Reformulate objective,
increase lower bound
Optimal
no
yes
PB lower bound derivation
Assume best case objective
PB call yields SAT?
Extract core
Reformulate objective,
increase lower bound
Optimal
no
yes
PB lower bound derivation
Assume best case objective
PB call yields SAT?
Extract core
Reformulate objective,
increase lower bound
Optimal
no
yes
PB lower bound derivation
Assume best case objective
PB call yields SAT?
Extract core
Reformulate objective,
increase lower bound
Optimal
no
yes
PB lower bound derivation
Assume best case objective
PB call yields SAT?
Extract core
Reformulate objective,
increase lower bound
Optimal
no
yes
PB lower bound derivation
Assume best case objective
PB call yields SAT?
Extract core
Reformulate objective,
increase lower bound
Optimal
no
yes
PB lower bound derivation
- Learned constraints yield objective bounds
- Fully automatic procedure
- "Dual" optimization method
Conclusion
- PB solvers learn full-blown cutting planes
- Theoretically superior to resolution
- and hence, to SAT/CP/ASP/SMT/...
- They perform cut generation using the division rule
- Constraint learning allows lower-bound optimization
- Efficient implementation: gitlab.com/JoD/exact
Thanks for your attention!
What use cases do you see for this kind of technology?
[MS96] GRASP - a new search algorithm for satisfiability - Marques-Silva, Sakallah
[MMZZM01] Chaff: Engineering an efficient SAT solver - Moskewicz, Madigan, Zhao, Zhang, Malik
[P04] Where are the hard knapsack problems? - Pisinger
[CK05] A fast pseudo-Boolean constraint solver - Chai, Kuehlmann
[SS06] Pueblo: A hybrid pseudo-Boolean SAT solver - Sheini, Sakallah
[ABKW08] Constraint Integer Programming: A New Approach to Integrate CP and MIP - Achterberg, Berthold, Koch, Wolter
[LP10] The Sat4j library, release 2.2 - Le Berre, Parrain
[EN18] Divide and conquer: Towards faster pseudo-boolean solving - Elffers, Nordström
[EGNV18] Using Combinatorial Benchmarks to Probe the Reasoning Power of pseudo-Boolean Solvers - Elffers, Giráldez-Cru, Nordström, Vinyals
[DGN20] Learn to Relax: Integrating 0-1 Integer Linear Programming with Pseudo-Boolean Conflict-Driven Search - Devriendt, Gleixner, Nordström
[D20] Watched Propagation for 0-1 Integer Linear Constraints - Devriendt
[JGDNS21] Cutting to the Core of Pseudo-Boolean Optimization: Combining Core-Guided Search with Cutting Planes Reasoning - Devriendt, Gocht, Demirovć, Nordström, Stuckey
[ZIB] SoPlex - soplex.zib.de
[PBCOMP] Latest PB competition - www.cril.univ-artois.fr/PB16/
[MIPLIB] The Mixed Integer Programming Library - miplib.zib.de
References
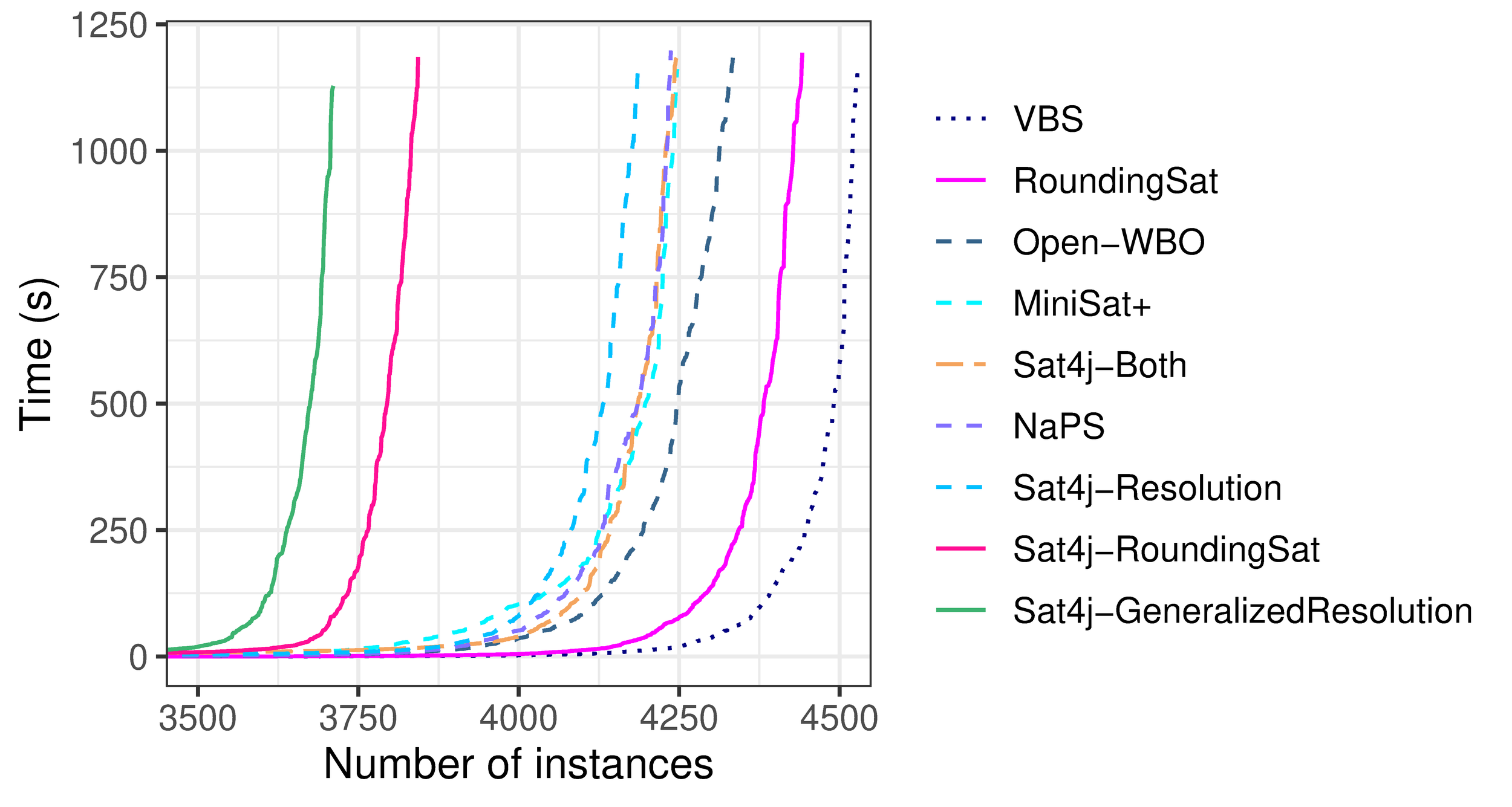
By Romain Wallon (CRIL, Univ Artois & CNRS)
RoundingSat (Exact) performance
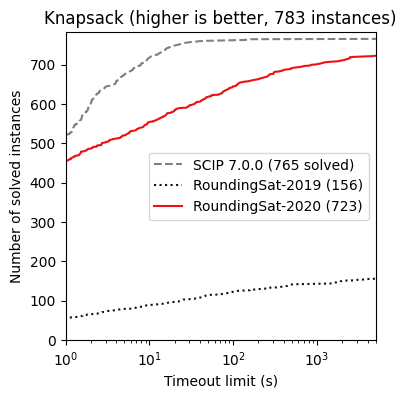
RoundingSat (Exact) performance

RoundingSat (Exact) performance
Constraint Reasoning, Pseudo-Boolean style
By Jo Devriendt
Constraint Reasoning, Pseudo-Boolean style
- 447



