Learn to Relax:
Integrating Integer Linear
Programming with
Conflict-Driven Search
Jo Devriendt †*, Ambros Gleixner ‡, Jakob Nordström *†
Acknowledgement: Jan Elffers †*
† Lund University, Sweden
‡ Zuse Institut Berlin, Germany
* University of Copenhagen, Denmark
jodevriendt.com
Conflict-driven search for 0-1 ILP
an example-driven intro
+x+y-z \geq 0 \\
-y+z-v \geq 0 \\
-z+2v-w \geq 0 \\
-x+y+w \geq 1 \\
x,y,z,v,w \mapsto \{0,1\}
Conflict-Driven Search Loop
- Input: 0-1 IL program
-
Output: either
- solution
- no solution exists
-
Search state:
- set of constraints φ
- partial assignment α
-
Initial state:
- φ = input
- α = {}
Conflict-Driven Search Loop
Unit propagation
- Under α, if a constraint c ∈ φ would be falsified by assuming x=0 (resp. x=1), extend α with x=1 (resp. x=0)
- Propagate until fixpoint
currently no unit propagation
\alpha=\{\}
+x+y-z \geq 0 \\
-y+z-v \geq 0 \\
-z+2v-w \geq 0 \\
-x+y+w \geq 1
Unit propagation
Conflict?
\alpha=\{\}
- Conflict: some c ∈ φ falsified by α
+x+y-z \geq 0 \\
-y+z-v \geq 0 \\
-z+2v-w \geq 0 \\
-x+y+w \geq 1
Conflict-Driven Search Loop
Unit propagation
Conflict?
Decide unassigned variable
no
- Only if unit propagation did not lead to a conflict
- If no unassigned variable left, return solution
- Resume unit propagation
\alpha=\{\}
+x+y-z \geq 0 \\
-y+z-v \geq 0 \\
-z+2v-w \geq 0 \\
-x+y+w \geq 1
Conflict-Driven Search Loop
Unit propagation
Conflict?
Decide unassigned variable
no
+x+y-z \geq 0 \\
-y+z-v \geq 0 \\
-z+2v-w \geq 0 \\
-x+y+w \geq 1
\alpha=\{x=0\}
- Only if unit propagation did not lead to a conflict
- If no unassigned variable left, return solution
- Resume unit propagation
Conflict-Driven Search Loop
Unit propagation
Conflict?
Decide unassigned variable
no
\alpha=\{x=0\}
+y-z \geq 0 \\
-y+z-v \geq 0 \\
-z+2v-w \geq 0 \\
+y+w \geq 1
Conflict-Driven Search Loop
Unit propagation
Conflict?
Decide unassigned variable
no
\alpha=\{x=0\}
+y-z \geq 0 \\
-y+z-v \geq 0 \\
-z+2v-w \geq 0 \\
+y+w \geq 1
Conflict-Driven Search Loop
Unit propagation
Conflict?
Decide unassigned variable
no
\alpha=\{x=0,y=1\}
+y-z \geq 0 \\
-y+z-v \geq 0 \\
-z+2v-w \geq 0 \\
+y+w \geq 1
Conflict-Driven Search Loop
Unit propagation
Conflict?
Decide unassigned variable
no
\alpha=\{x=0,y=1\}
+1-z \geq 0 \\
-1+z-v \geq 0 \\
-z+2v-w \geq 0 \\
+1+w \geq 1
Conflict-Driven Search Loop
Unit propagation
Conflict?
Decide unassigned variable
no
\alpha=\{x=0,y=1,\\z=1,v=0\}
+1-z \geq 0 \\
-1+z-v \geq 0 \\
-z+2v-w \geq 0 \\
+1+w \geq 1
Conflict-Driven Search Loop
Unit propagation
Conflict?
Decide unassigned variable
no
\alpha=\{x=0,y=1,\\z=1,v=0\}
0 \geq 0 \\
0 \geq 0 \\
-1-w \geq 0 \\
+1+w \geq 1
Conflict-Driven Search Loop
Unit propagation
Conflict?
Decide unassigned variable
no
\alpha=\{x=0,y=1,\\z=1,v=0\}
0 \geq 0 \\
0 \geq 0 \\
-1-w \geq 0 \\
+1+w \geq 1
- Conflict: some constraint in φ falsified by α
Conflict-Driven Search Loop
Unit propagation
Conflict?
Learn constraint
Decide unassigned variable
yes
no
- From falsified constraint and reasons, construct learned constraint
- implied by φ, should prevent conflict
- Add learned constraint to φ
- → learned constraint database
\alpha=\{x=0,y=1,\\z=1,v=0\}
0 \geq 0 \\
0 \geq 0 \\
-1-w \geq 0 \\
+1+w \geq 1
Conflict-Driven Search Loop
Unit propagation
Conflict?
Learn constraint
Decide unassigned variable
yes
no
\alpha=\{x=0,y=1,\\z=1,v=0\}
-2y+z-w \geq 0
- From falsified constraint and reasons, construct learned constraint
- implied by φ, should prevent conflict
- Add learned constraint to φ
- → learned constraint database
+x+y-z \geq 0 \\
-y+z-v \geq 0 \\
-z+2v-w \geq 0 \\
-x+y+w \geq 1
\textcolor{red}{2\times}
\textcolor{red}{1\times}
\textcolor{red}{+}
Conflict-Driven Search Loop
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
- Backtrack based on learned constraint
- Resume unit propagation
\alpha=\{x=0,y=1,\\z=1,v=0\}
-2y+z-w \geq 0
+x+y-z \geq 0 \\
-y+z-v \geq 0 \\
-z+2v-w \geq 0 \\
-x+y+w \geq 1
Conflict-Driven Search Loop
- Backtrack based on learned constraint
- Resume unit propagation
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
- Backtrack based on learned constraint
- Resume unit propagation
\alpha=\{\}
-2y+z-w \geq 0
+x+y-z \geq 0 \\
-y+z-v \geq 0 \\
-z+2v-w \geq 0 \\
-x+y+w \geq 1
Conflict-Driven Search Loop
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
\alpha=\{\}
+x+y-z \geq 0 \\
-y+z-v \geq 0 \\
-z+2v-w \geq 0 \\
-x+y+w \geq 1
-2y+z-w \geq 0
Conflict-Driven Search Loop
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
-2y+z-w \geq 0
+x+y-z \geq 0 \\
-y+z-v \geq 0 \\
-z+2v-w \geq 0 \\
-x+y+w \geq 1
\alpha=\{y=0\}
Conflict-Driven Search Loop
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
+x-z \geq 0 \\
+z-v \geq 0 \\
-z+2v-w \geq 0 \\
-x+w \geq 1
+z-w \geq 0
\alpha=\{y=0\}
Conflict-Driven Search Loop
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
\alpha=\{y=0,w=1,\\x=0\}
-z \geq 0 \\
+z-v \geq 0 \\
-z+2v-1 \geq 0 \\
1 \geq 1
+z-1 \geq 0
Conflict-Driven Search Loop
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
\alpha=\{y=0,w=1,\\x=0,z=0\}
0 \geq 0 \\
-v \geq 0 \\
+2v-1 \geq 0 \\
1 \geq 1
-1 \geq 0
Conflict-Driven Search Loop
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
\alpha=\{y=0,w=1,\\x=0,z=0\}
0 \geq 0 \\
-v \geq 0 \\
+2v-1 \geq 0 \\
1 \geq 1
-1 \geq 0
Conflict-Driven Search Loop
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
0 \geq 1
-2y+z-w \geq 0
+x+y-z \geq 0 \\
-y+z-v \geq 0 \\
-z+2v-w \geq 0 \\
-x+y+w \geq 1
\alpha=\{y=0,w=1,\\x=0,z=0\}
Conflict-Driven Search Loop
\textcolor{red}{+}
\textcolor{red}{+}
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
0 \geq 1
Unsatisfiable!
-2y+z-w \geq 0
+x+y-z \geq 0 \\
-y+z-v \geq 0 \\
-z+2v-w \geq 0 \\
-x+y+w \geq 1
\alpha=\{y=0,w=1,\\x=0,z=0\}
Conflict-Driven Search Loop
\textcolor{red}{+}
\textcolor{red}{+}
Unit propagation
Conflict?
Learn constraint
Backjump
Decide unassigned variable
yes
no
- Learning constraints pushes search forward
- Thousands of conflicts per second
- Highly optimized unit propagation
- Originates from Boolean satisfiability (SAT) [MS96,BS97,MMZZM01]
- Generalized to pseudo-Boolean (PB) solving [CK05,SS06,LP10,EN18]
- many variations possible
here be dragons
Conflict-Driven Search Loop
Another look at our example...
+x+y-z \geq 0 \\
-y+z-v \geq 0 \\
-z+2v-w \geq 0 \\
-x+y+w \geq 1 \\
x,y,z,v,w \mapsto \{0,1\}
- It's rationally infeasible!
- Could be solved without search
- In theory: rationally infeasible programs are easy for conflict-driven PB search
- In practice: PB solvers timeout on certain rationally infeasible programs [EGNV18]
- unit propagation is local
- wrong constraints are learned
How about integrating an LP solver?
our work
Linear Programming (LP) solver
- Input:
- LP relaxation of φ
- variable bounds α
- objective function
- Output: either
- optimal rational solution
-
Farkas multipliers
- define a positive linear combination of constraints
in φ, falsified by α
- define a positive linear combination of constraints
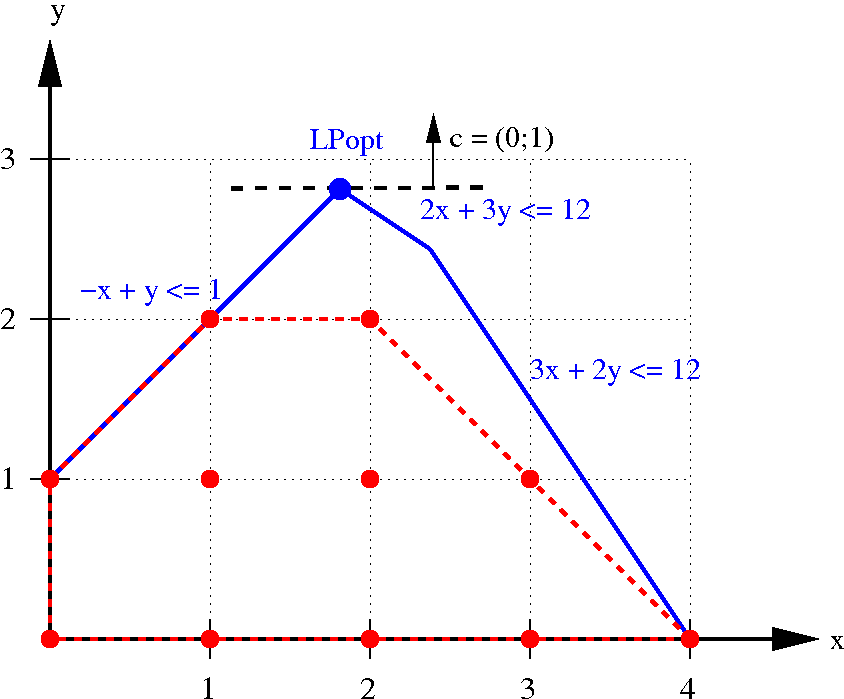
Conflict-Driven Search Loop
with LP solver call
Unit Propagation
Conflict?
Backjump
Decide unassigned variable
no
Rational infeasibility?
Query LP solver
yes
no
Learn constraint
Extract Farkas multipliers
yes
Learn Farkas constraint
Rational infeasibility example
\textcolor{red}{+a}+x+y-z \geq 0 \\
\textcolor{red}{+b}-y+z-v \geq 0 \\
-z+2v-w \geq 0 \\
-x+y+w \geq 1 \\
\textcolor{red}{+a-b \geq 0}
\alpha=\{a=0,b=0\}
\textcolor{red}{\times 1}\\
\textcolor{red}{\times 2}\\
\textcolor{red}{\times 1}\\
\textcolor{red}{\times 1}\\
\textcolor{red}{\times 0}\\
+a+2b\geq 1
Farkas multipliers
conflicting
Farkas constraint
- LP solvers are slow compared to conflict-driven search loop
- limit calls to LP solver
- limit LP solver running time
- deterministic measure: balance #conflicts in conflict-driven solver to #pivots in LP solver
- LP solver uses inexact floating point arithmetic
- learned constraint must be implied by φ
- calculate Farkas constraint with exact arithmetic
- verify Farkas constraint is still conflicting
- post-process Farkas constraint to eliminate noise
Two technical hurdles
- Every once in a while, run LP solver to completion at root
- use (optimal) rational solution as value heuristic
- generate Chvátal-Gomory (CG) cuts
- add to both LP solver and learned constraint set
- Generate "deep" Chvátal-Gomory cuts from internal search nodes
- valid at root node, so safe to add as learned constraint
- Add learned constraints as cuts to the LP solver
Further ideas
- PB solver RoundingSat [EN18]
- Strong ILP constraint learning
- Performed well in past PB competitions
- Linear optimization built on top of conflict-driven search loop
- LP solver SoPlex [ZIB]
- SCIP's native LP solver
- State-of-the-art open source
Working implementation
- #pivots/#conflicts ≤ 1
- 128 bit precision to calculate CG cuts and Farkas constraints
- Cut parallelism check
- for decision instances, minimize sum of variables in SoPlex
- for pure CNFs, deactivate LP techniques
Design choices
Compare state-of-the-art
- RoundingSat
- Sat4J
- NaPS
- SCIP
- Gurobi
- CPLEX
to implementations
- RS+SPX
- RS+SPX+GC
- RS+SPX+GC+LC
Experiments!
[PBCOMP]
[PBCOMP]
[PBCOMP]
[PBCOMP]
[P04]
[P04]
[MIPLIB]
[MIPLIB]
[MIPLIB]
[MIPLIB]
Related work
- Combined conflict analysis and LP solving in other solving paradigms:
- SAT: LPSAT [WW00]
- CP: LCG-Glucose [D16]
- SMT: deciding linear arithmetic [Dd06]
- MIP: SAT-style learning, e.g. SCIP [ABKW08]
- Key differences of our approach:
- run LP solver incrementally
- not until completion
-
native conflict analysis on all linear constraints
- exponentially stronger than clausal conflict analysis
- run LP solver incrementally
Summary
Conflict-driven search for 0-1 ILPs
- Generates cuts from search conflicts
- Does not always find short refutations for rational infeasibility
- Allows sound & efficient integration with LP solver
- Is further improved by value heuristic & Gomory cut generation
Thanks for your attention!
Experiments approach best of both worlds
[MS96] GRASP - a new search algorithm for satisfiability - Marques-Silva, Sakallah
[BS97] Using CSP lookback techniques to solve real-world SAT instances - Bayardo, Schrag
[WW00] Combining Linear Programming and Satisability Solving for Resource Planning - Wolfman, Weld
[MMZZM01] Chaff: Engineering an efficient SAT solver - Moskewicz, Madigan, Zhao, Zhang, Malik
[P04] Where are the hard knapsack problems? - Pisinger
[CK05] A fast pseudo-Boolean constraint solver - Chai, Kuehlmann
[SS06] Pueblo: A hybrid pseudo-Boolean SAT solver - Sheini, Sakallah
[Dd06] A Fast Linear-Arithmetic Solver for DPLL(T) - Dutertre, de Moura
[ABKW08] Constraint Integer Programming: A New Approach to Integrate CP and MIP - Achterberg, Berthold, Koch, Wolter
[LP10] The Sat4j library, release 2.2 - Le Berre, Parrain
[D16] Scheduling and rostering with learning constraint solvers - Downing
[EN18] Divide and conquer: Towards faster pseudo-boolean solving - Elffers, Nordström
[EGNV18] Using Combinatorial Benchmarks to Probe the Reasoning Power of pseudo-Boolean Solvers - Elffers, Giráldez-Cru, Nordström, Vinyals
[ZIB] SoPlex - soplex.zib.de
[PBCOMP] Latest PB competition - www.cril.univ-artois.fr/PB16/
[MIPLIB] The Mixed Integer Programming Library - miplib.zib.de
References
Learn to Relax: Integrating Integer Linear Programming with Conflict-Driven Search - CPAIOR
By Jo Devriendt
Learn to Relax: Integrating Integer Linear Programming with Conflict-Driven Search - CPAIOR
Learn to Relax: Integrating Linear Programming with Conflict-Driven Search
