Joost Jorritsma,
joint with Tim Hulshof and Júlia Komjáthy
Long connections carry the curve
This talk is about
- Epidemics like COVID-19
- Theoretical epidemiology
- What classical models lack
- Effect of space/geometry/geography
- Effect of social distancing
- Long-term effects
This talk is not about
- Predictions for COVID-19
- Precise modeling of COVID-19
Outline
- Classical models vs. Network-based
- Intervention strategies
Compartmental model
Susceptible
Infected
Recovered
- ODE: Analytic expression \(I(t), S(t), R(t)\)
- Additional states could be added (Richard)
- "Mean-field" model: everything is averaged out:
individuals are equal, everybody is weakly connected, individuals are "real-valued"
Two phases:
- Subcritical: \(R_0=\beta/\gamma\le1\): epidemic vanishes
- Supercritical: \(R_0>1\): exponential incline
Compartmental model
- Additional states could be added (Richard)
- "Mean-field" model: everything is averaged out:
individuals are equal, everybody is weakly connected, individuals are "real-valued"
- Only way of modeling interventions:
Set \(\beta:=\beta(t), \gamma:=\gamma(t), N:=N(t)\). - Unclear how and why interventions work (assuming no data is available)
- What is the most effective intervention?
Susceptible
Infected
Recovered
Network-based approach
Susceptible
Infected
Recovered
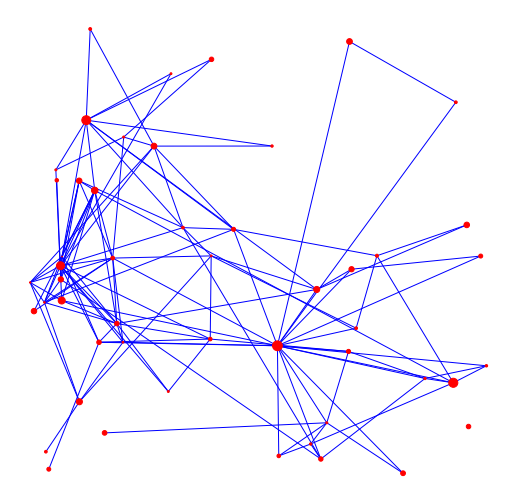
Infect neighbor w.p. \(\beta\)
Heal w.p. \(\gamma\)
- Contact network as a graph
- Infectious nodes infect neighbors
- Models "coincide" for complete graph and scaling \(\beta\)
- Interventions: remove edges
Network-based approach
Susceptible
Infected
Recovered
Heal w.p. \(\gamma\)
- Contact network as a graph
- Infectious nodes infect neighbors
- Models "coincide" for complete graph and scaling \(\beta\)
- Interventions: remove edges
- At random (social dist.)
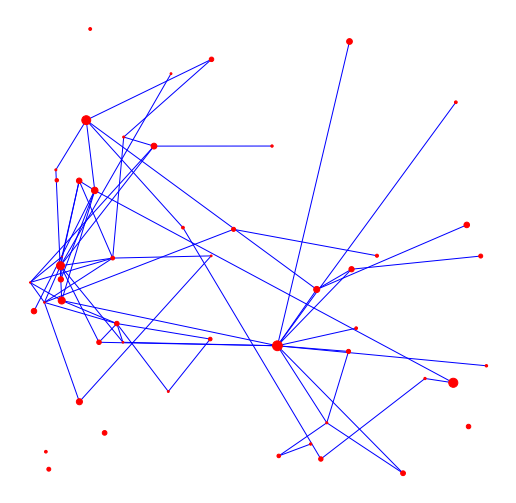
Infect neighbor w.p. \(\beta\)
Network-based approach
Susceptible
Infected
Recovered
Heal w.p. \(\gamma\)
- Contact network as a graph
- Infectious nodes infect neighbors
- Models "coincide" for complete graph and scaling \(\beta\)
- Interventions: remove edges
- At random (social dist.)
- Euclidean length (no travel)
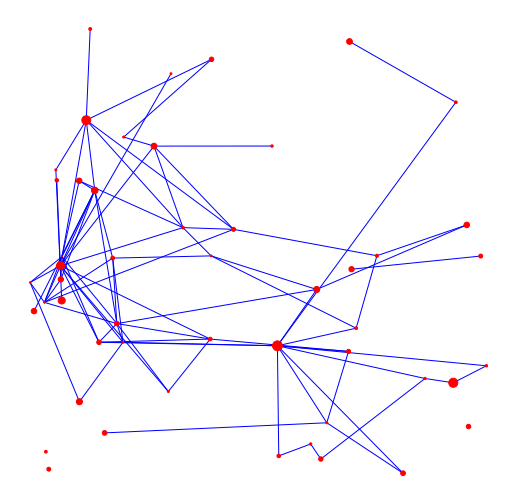
Infect neighbor w.p. \(\beta\)
Network-based approach
Susceptible
Infected
Recovered
Heal w.p. \(\gamma\)
- Contact network as a graph
- Infectious nodes infect neighbors
- Models "coincide" for complete graph and scaling \(\beta\)
- Interventions: remove edges
- At random (social dist.)
- Euclidean length (no travel)
- Degree (limit # contacts)
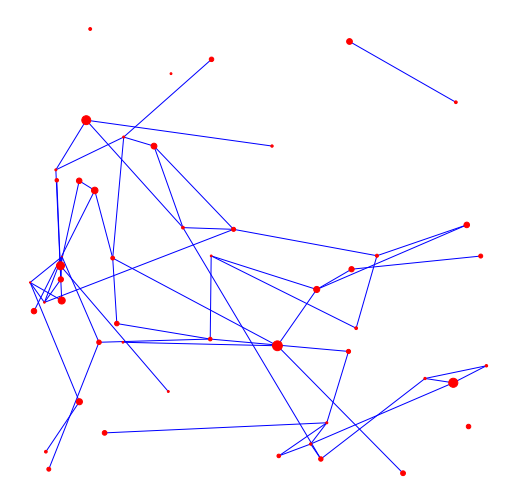
Infect neighbor w.p. \(\beta\)
Network-based approach




No int.
Social dist.
No travel
No hubs
Classical vs. Network
| Classical | Network |
|---|---|
| Only two parameters | Underlying network |
| Deterministic | Stochastic |
| "Mean-field" | Variability between nodes |
| No spatial component | Spatial component possible |
| Intuitive modeling intervention | |
| Analytic expression |
Network approach
Susceptible
Infected
Recovered
Infect neighbor w.p. \(\beta\)
Heal w.p. \(\gamma\)
Susceptible w.p. \(\eta\)
- Immunity unclear for COVID-19
- Natural model for "second" peaks
(also for classical model)
Network approach
Network topology
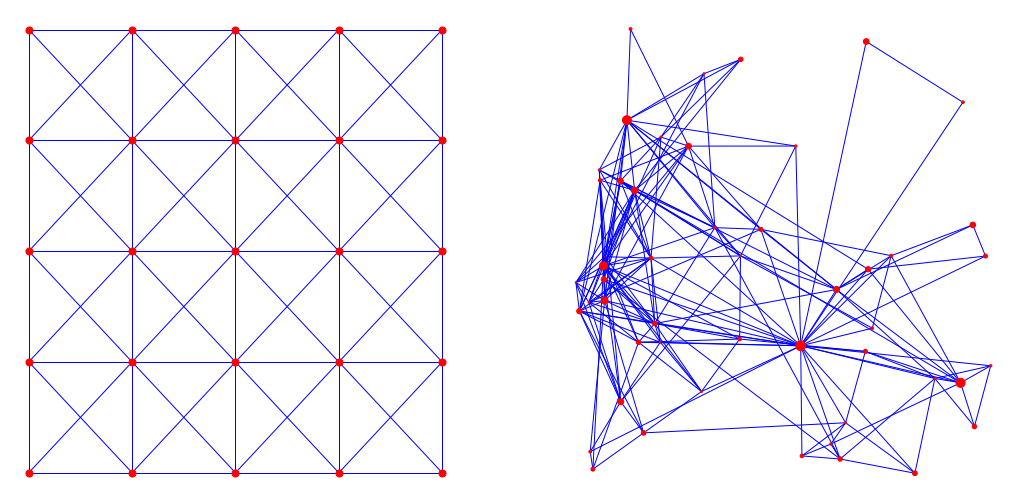
Two graphs with mean degree 8
Network approach
Network topology
Mean degree 8, 160000 nodes
Network approach
Network topology

Two graphs with mean degree 8
Polynomial growth
"Faster" growth
Network approach
Network topology

Desired features
- "close" nodes are
likely to be connected - High variability in degrees
- "Important" nodes are
likely to be connected
Random graph model (\(\alpha>1\)):
Results
- Network vs. Compartmental
- New phases
- Oscillations
-
Effect of social dist., no travel, no hubs
- How to compare?
- First peak
- Later peaks
- Probability of survival
Supercritical epidemic dies out in network for \(\eta\) small
Single peak, extinction
large graphs, 100 runs
Survival
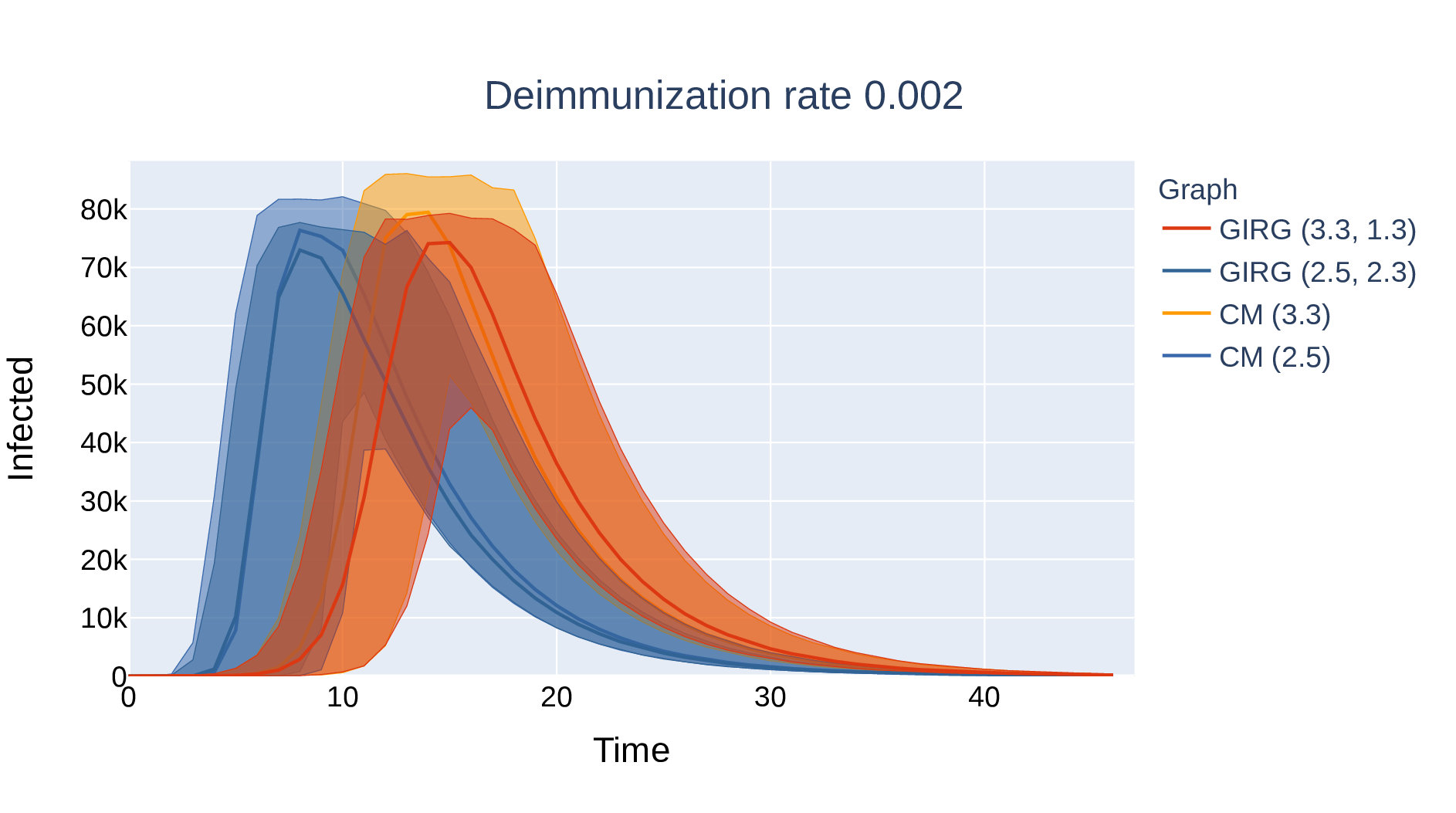

Four networks
Compartmental,
\(\eta\) small and large
Geometry introduces "immunity boundaries", herd immunity
Supercritical epidemic can survive in network for \(\eta\) large
Four networks
Compartmental,
\(\eta\) small and large
Single peak, survival
large graphs, 100 runs
Survival


Supercritical epidemic can survive in network for \(\eta\) large
Oscillations in three networks
Absence of long edges: larger amplitude

Results
-
Network vs. Compartmental
- New phases
- Oscillations
-
Effect of social dist., no travel, no hubs
- How to compare?
- First peak
- Later peaks
- Probability of survival
Comparing interventions
- Remove edges permanently
according to "rule":- Social dist: Random
- No travel: Long edges
- No hubs: Removing edges from large-degree nodes
- Match parameters s.t. average degree is comparable
- Start epidemic from single node
- Resulting epidemic has at least one peak
Comparing interventions

No int. (4.8)

Social dist. (2.6)


No hubs (2.6)
No travel (2.6)
No travel works best for the first peak

Average distance from logarithmic to polynomial
No travel works best for the first peak
Average distance from logarithmic to polynomial

No travel works well for later peaks
Higher degree-spread diminishes amplitude

No travel works well for later peaks
Higher degree-spread diminishes amplitude

Summary
Epidemics on networks with underlying geometry
- are different from classical models.
- allow for intuitive modeling of interventions (if no historical data is available).
Travel restriction works best after supercritical intervention (in a model with temporary immunity)
- because it drastically increases average graph distance.
- if interventions are maintained permanently and possible to implement.
- assuming that the underlying graph is a good representation.
Corona GIRG Interventions 1
By joostjor
Corona GIRG Interventions 1
- 565



