初探演算法
自我介紹
成電37 蔡孟平
口齒不清、表達能力不佳,請各位多多包涵
如果有不懂,就直接問
或是覺得哪裡講錯,就請電神賜教了
喜歡打籃球、寫一些題目
宅
數學小知識
對數 log
logₐb 讀作 以 aaa 為底的 bbb 的對數
對數 log
logₐb 讀作 以 aaa 為底的 bbb 的對數
其實就是 a 的多少次方會等於b
對數 log
logₐb 讀作 以 aaa 為底的 bbb 的對數
其實就是 a 的多少次方會等於b
ex :
log₂ 1024 = 10
log₁₀ 1000000000 = 9
屬於 ∊
設一集合A中又有
{1,2,65,9,12}
可以說 2 ∊ A
階乘 !
n! = 1*2*3 ......*(n-1)*n
階乘 !
n! = 1*2*3 ......*(n-1)*n
ex:
3! = 6
7! = 5040
15! = 1307674368000
什麼是演算法?
先看看維基中的定義
因為我也不太清楚
一個有被定義步驟,可以解決特定問題的方法
排序演算法
泡沫排序法
Bubble sort
倆倆比較相鄰元素,如果右大於左就交換
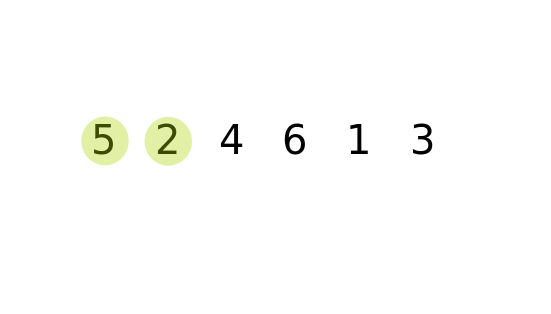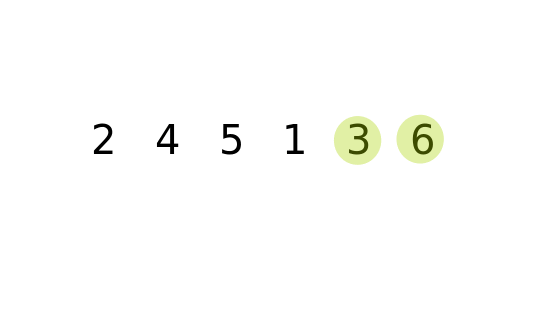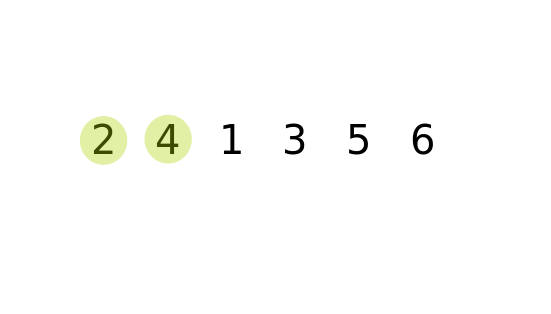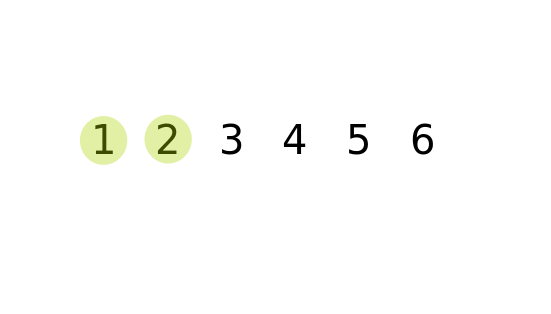
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
這樣做完一輪
要做N輪
為什麼?
int main() {
int n; cin>>n;
int arr[n+1];
for(int i=1;i<=n;++i) cin>>arr[i];
for(int i=0;i<n;++i){
for(int j=1;j<n;++j){
if(arr[j] > arr[j+1]) swap(arr[j],arr[j+1]);
}
}
for(int i=1;i<=n;++i) cout<<arr[i]<<' ';
}插入排序法
Insertion sort
假設前 i 個元素已排序過的,把第 i+1 的元素排入前 i 個元素中
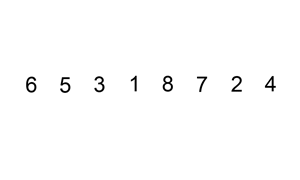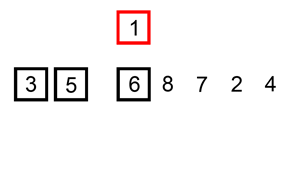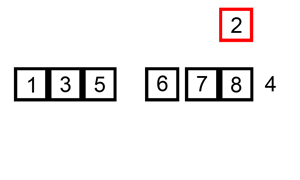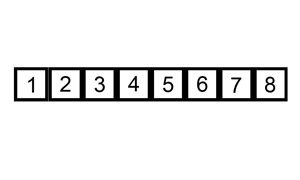
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
完成 !!!
int main() {
int n; cin>>n;
int arr[n+1];
for(int i=1;i<=n;++i) cin>>arr[i];
for (int i = 2; i <= n; i++) {
int current = arr[i];
int j = i - 1;
while (j > 0 && arr[j] > current) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = current;
}
for(int i=1;i<=n;++i) cout<<arr[i]<<' ';
}合併排序法
Merge sort
先倆兩排,再四四排,......,不斷把已排序過的合併
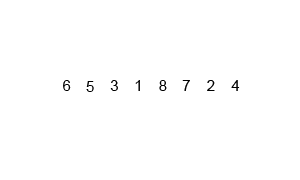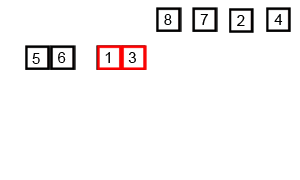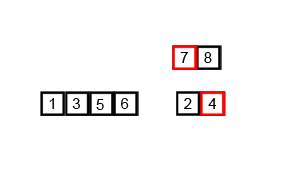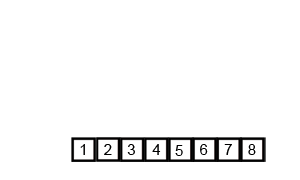
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
3
8
4
7
1
5
3
6
merge sort ㄉ 摳
void merge(int arr[], int l, int m, int r) {
int n1 = m - l + 1, n2 = r - m;
int L[n1 + 1], R[n2 + 1];
for (int i = 1; i <= n1; i++) L[i] = arr[l + i - 1];
for (int i = 1; i <= n2; i++) R[i] = arr[m + i];
int i = 1, j = 1, k = l;
while (i <= n1 && j <= n2) arr[k++] = (L[i] <= R[j]) ? L[i++] : R[j++];
while (i <= n1) arr[k++] = L[i++];
while (j <= n2) arr[k++] = R[j++];
}
void mergeSort(int arr[], int l, int r) {
if (l >= r) return;
int m = l + (r - l) / 2;
mergeSort(arr, l, m);
mergeSort(arr, m + 1, r);
merge(arr, l, m, r);
}
int main() {
int n; cin>>n;
int arr[n+1];
for(int i=1;i<=n;++i) cin>>arr[i];
mergeSort(arr, 1, n);
for(int i=1;i<=n;++i) cout<<arr[i]<<' ';
return 0;
}快速排序法
Quick sort
隨便抓一個元素當作標準,把大於它的丟右邊,小於它的丟左邊
繼續在左右做同樣的事情

3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
3
8
4
7
1
5
int part(int arr[], int l, int r) {
int standerd = arr[r];
int i = l - 1;
for (int j = l; j < r; j++) {
if (arr[j] <= standerd) {
i++;
swap(arr[i], arr[j]);
}
}
swap(arr[i + 1], arr[r]);
return i + 1;
}
void quickSort(int arr[], int l, int r) {
if(l>=r) return;
int pi = part(arr, l, r);
quickSort(arr, l, pi - 1);
quickSort(arr, pi + 1, r);
}
int main() {
int n; cin>>n;
int arr[n];
for(int i=1;i<=n;++i) cin>>arr[i];
quickSort(arr, 1, n);
for(int i=1;i<=n;++i) cout<<arr[i]<<' ';
return 0;
}扣
基數排序法
Radix sort
想像有10個籃子,分別代表0~9,從個位開始將數字放到對應的
籃子中,在依序從0~9籃子取出,接著對十位做,以此類推
33
48
14
27
91
85
0 1 2 3 4 5 6 7 8 9
33
48
14
27
91
85
0 1 2 3 4 5 6 7 8 9
33
48
14
27
91
85
0 1 2 3 4 5 6 7 8 9
33
48
14
27
91
85
0 1 2 3 4 5 6 7 8 9
33
48
14
27
91
85
0 1 2 3 4 5 6 7 8 9
33
48
14
27
91
85
0 1 2 3 4 5 6 7 8 9
33
48
14
27
91
85
0 1 2 3 4 5 6 7 8 9
33
48
14
27
91
85
0 1 2 3 4 5 6 7 8 9
33
48
14
27
91
85
0 1 2 3 4 5 6 7 8 9
33
48
14
27
91
85
0 1 2 3 4 5 6 7 8 9
33
48
14
27
91
85
0 1 2 3 4 5 6 7 8 9
33
48
14
27
91
85
0 1 2 3 4 5 6 7 8 9
33
48
14
27
91
85
0 1 2 3 4 5 6 7 8 9
33
48
14
27
91
85
0 1 2 3 4 5 6 7 8 9
33
48
14
27
91
85
0 1 2 3 4 5 6 7 8 9
33
48
14
27
91
85
0 1 2 3 4 5 6 7 8 9
33
48
14
27
91
85
0 1 2 3 4 5 6 7 8 9
33
48
14
27
91
85
0 1 2 3 4 5 6 7 8 9
33
48
14
27
91
85
0 1 2 3 4 5 6 7 8 9
33
48
14
27
91
85
0 1 2 3 4 5 6 7 8 9
33
48
14
27
91
85
0 1 2 3 4 5 6 7 8 9
33
48
14
27
91
85
0 1 2 3 4 5 6 7 8 9
33
48
14
27
91
85
0 1 2 3 4 5 6 7 8 9
33
48
14
27
91
85
0 1 2 3 4 5 6 7 8 9
33
48
14
27
91
85
0 1 2 3 4 5 6 7 8 9
可以想像成是
從小的位數開始排,每次排序不打亂原有順序

只能排序整數 QQ
最後介紹一個雖然不太實用,但很有趣的排序法
有沒有一種排序法,不須比較、交換、或是剛剛的分類(放籃子)
睡覺排序法
sleep sort
3
8
4
7
1
5
timer : 0s
3
8
4
7
1
5
timer : 1s
3
8
4
7
1
5
timer : 2s
3
8
4
7
1
5
timer : 3s
3
8
4
7
1
5
timer : 4s
3
8
4
7
1
5
timer : 5s
3
8
4
7
1
5
timer : 6s
3
8
4
7
1
5
timer : 7s
3
8
4
7
1
5
timer : 8s
對於以上幾個排序法大家有什麼問題嗎?
你們認為哪個方法比較好呢??
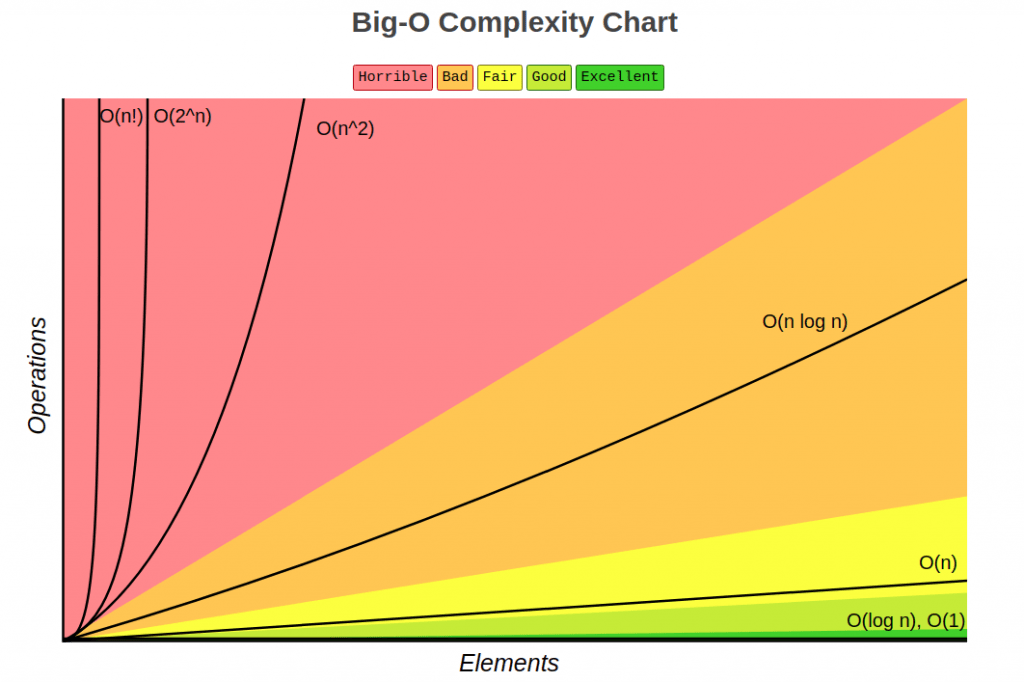
如何分析、比較演算法的好壞?
Complexity
花的時間少 ?
哪一個演算法比較好?
花的時間少 ?
哪一個演算法比較好?
用的空間少 ?
花的時間少 ?
哪一個演算法比較好?
用的空間少 ?
正確率高低?
如何預測 ?
正確率 :
實作細節、邊界情況、理論分析
如何預測 ?
正確率 :
實作細節、邊界情況、理論分析
空間 :
使用的資料結構、最大資料大小
如何預測 ?
正確率 :
實作細節、邊界情況、理論分析
空間 :
使用的資料結構、最大資料大小
時間?
時間 :
不同的操作會花不同的時間
ex : 乘法比除法快
時間 :
不同的操作會花不同的時間
ex : 乘法比除法快
在不同的機器上運行的時間也不一樣
ex : 電腦可能比手機快
時間 :
不同的操作會花不同的時間
ex : 乘法比除法快
在不同的機器上運行的時間也不一樣
ex : 電腦可能比手機快
資料的大小不同時,也會有不同結果
ex : A : 8n² B : 100n
時間 :
不同的操作會花不同的時間
ex : 除法比乘法快
在不同的機器上運行的時間也不一樣
ex : 電腦可能比手機快
資料的大小不同時,也會有不同結果
ex : A : 8n² B : 100n
但其實真正要在意的是當 n 很大的時候 !!!
為什麼 ??
| n²+2n+5 | 20n + 100 | |
|---|---|---|
| n = 5 | 40 | 180 |
| n = 22 | 533 | 540 |
| n = 100 | 10205 | 2100 |
有一台電腦
每秒能做1000次加法
A B
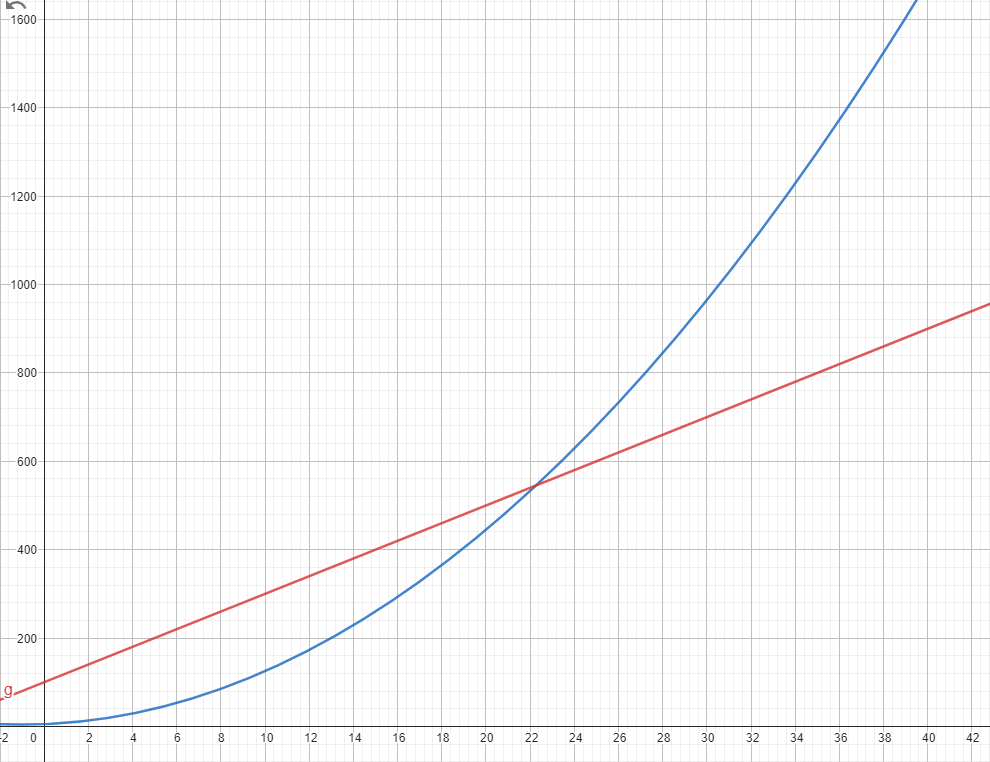
複雜度概念
比較它們成長的速度
兩個函數 f(x) 、 g(x) ,當x接近∞時誰比較大
複雜度概念
考一考 :
3x² + x vs 100x
500x + 10⁵ vs 30x³
3n vs 30000 log₂n
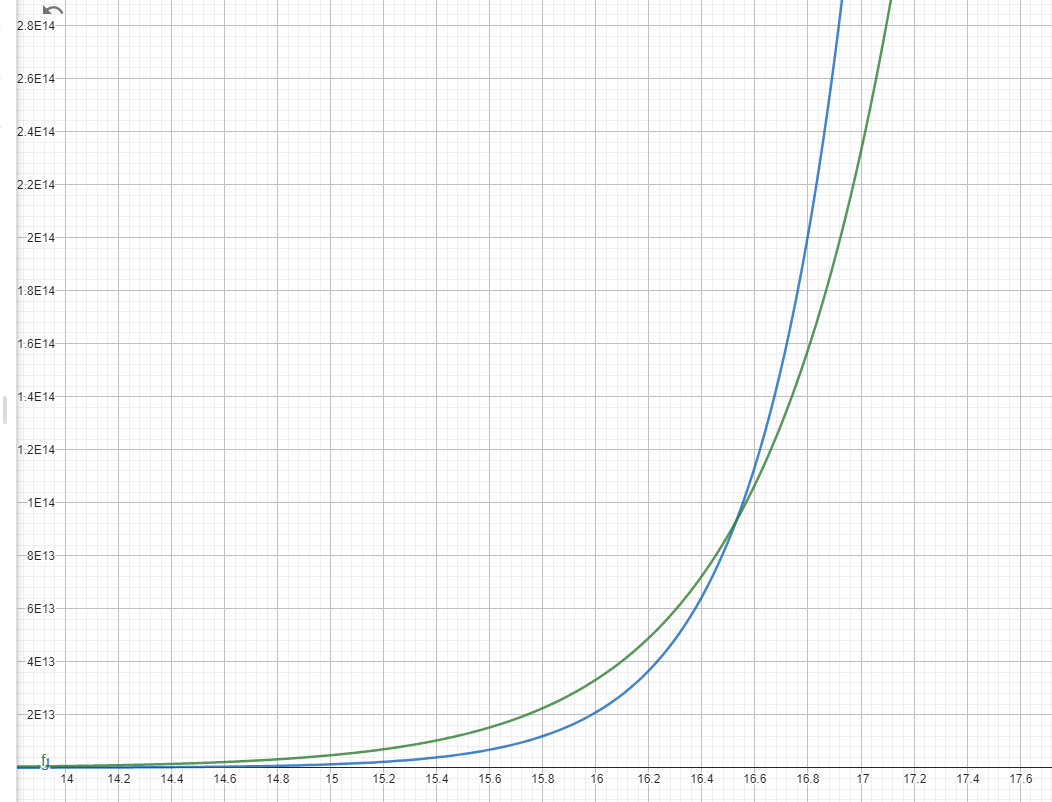
2ⁿ vs n⁹
7ⁿ vs n!
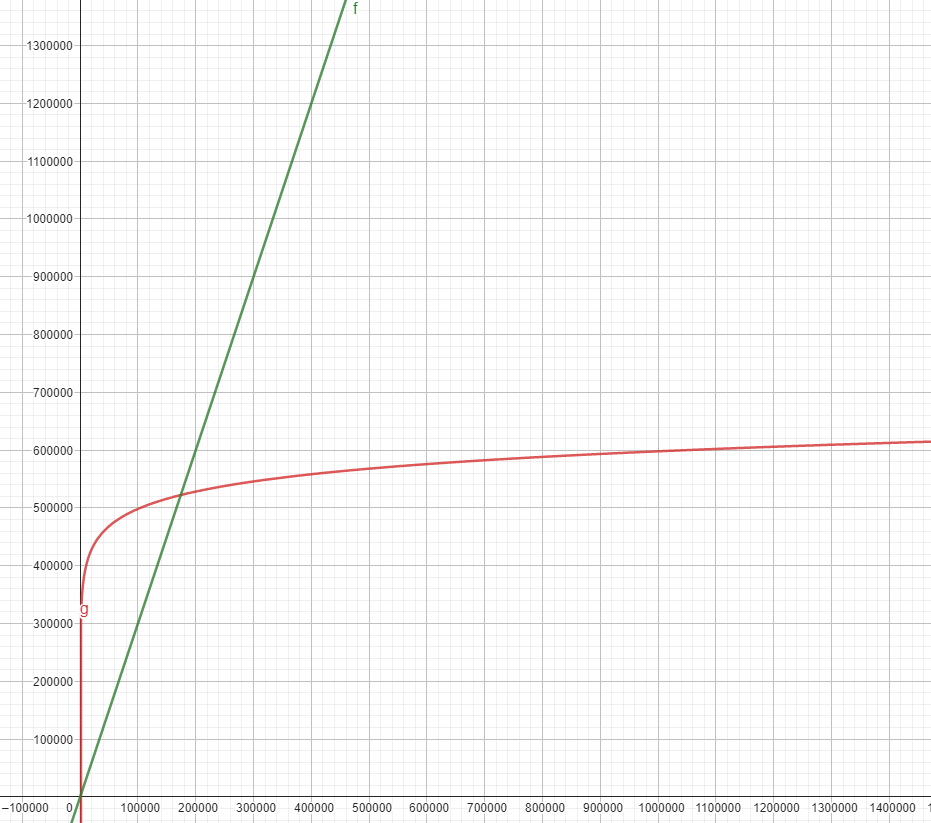
3n vs 30000 log₂n
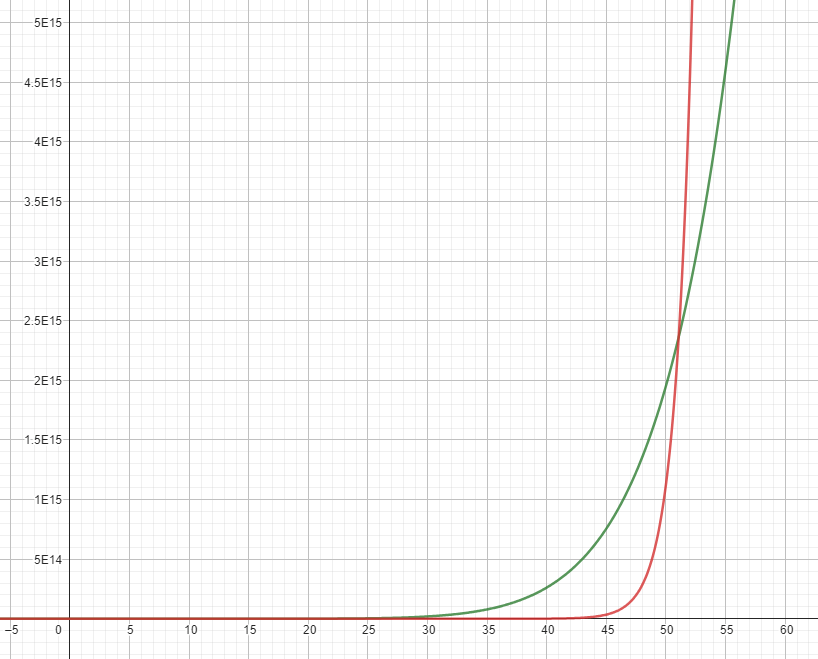
2ⁿ vs n⁹
7ⁿ vs n!
複雜度概念
每種操作花費的時間不同,但都是常數時間,因此先視為一樣
包括 : 加減乘除、位元運算、存取記憶體......
複雜度概念
每種操作花費的時間不同,但都是常數時間,因此先視為一樣
包括 : 加減乘除、位元運算、存取記憶體......
我們把所有操作的次數加起來,看看大概它的數量級
複雜度概念
每種操作花費的時間不同,但都是常數時間,因此先視為一樣
包括 : 加減乘除、位元運算、存取記憶體......
我們把所有操作的次數加起來,看看大概它的數量級
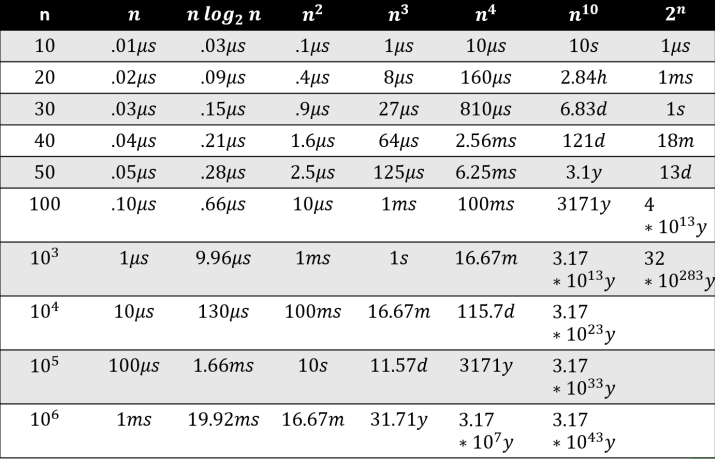
ex:
假設一程式測資大小為 n ,與操作總次數的關係為
3n² + 400n + 500 則當n=100時
操作總次數大概為 70500 的常數倍
剛剛的例子 3n² + 400n + 500
當n很大時,例如n=1e4
代入上式 = 3e8 + 4e6 + 500
剛剛的例子 3n² + 400n + 500
當n很大時,例如n=1e4
代入上式 = 3e8 + 4e6 + 500
可以發現其實 n² 才是影響大小的主因
剛剛的例子 3n² + 400n + 500
當n很大時,例如n=1e4
代入上式 = 3e8 + 4e6 + 500
可以發現其實 n² 才是影響大小的主因
因此最後的複雜度以 O(n²) 表示
Big-O 符號
我們把時間或空間複雜度寫成O(f(n))
Big-O 符號
我們把時間或空間複雜度寫成O(f(n)),
其中f(n)代表複雜度量級的上界
ex :
4n⁴ + 50n³ + 6n + 9 ∊ O(n⁴)
f(n) ∊ O(n²) 則 f(n) ∊ O(n⁴)
99999999999 ∊ O(1)
我們通常關注最差的case來分析複雜度
Big-O 符號
我們通常關注最差的case來分析複雜度
Big-O 符號
ex :
case 1 : aaaaaa、abaaaa
case 2 : bbbbbb、bbbbba
這樣做的時間複雜度還是會寫成O(n)
Big-O 符號
加法 :
O(f(n)) + O(g(n)) = O(max(f(n), g(n)))
Big-O 符號
加法 :
O(f(n)) + O(g(n)) = O(max(f(n), g(n)))
乘法 :
O(f(n)) * O(g(n)) = O(f(n)*g(n))
練習時間
n¹⁰ + 50 vs 3ⁿ + 50n
O(n¹⁰) vs O(3ⁿ)
練習時間
n¹⁰ + 50 vs 3ⁿ + 50n
O(n¹⁰) vs O(3ⁿ)
7n! + n³⁰ vs 10ⁿ + 50000
O(n!) vs O(10ⁿ)
練習時間
n¹⁰ + 50 vs 3ⁿ + 50n
O(n¹⁰) vs O(3ⁿ)
7n! + n³⁰ vs 10ⁿ + 50000
O(n!) vs O(10ⁿ)
O(n) + O(nlogn) + O(n!) + O(2ⁿ) =
看點具體的例子
講了那麼多,那要如何判斷一個程式的複雜度呢
講了那麼多,那要如何判斷一個程式的複雜度呢
就是把大概操作次數加起來
數迴圈等,操作次數受輸入大小影響的地方
直接看範例
int main(){
int cnt = 0;
for(int i=0;i<n;++i){
cnt++;
}
for(int i=0;i<n;++i){
for(int k=0;k<n;++k){
cnt++;
}
}
for(int i=1;i<n;i<<=1){
for(int k=0;k<n;++k){
cnt++;
}
}
}O(n)
直接看範例
int main(){
int cnt = 0;
for(int i=0;i<n;++i){
cnt++;
}
for(int i=0;i<n;++i){
for(int k=0;k<n;++k){
cnt++;
}
}
for(int i=1;i<n;i<<=1){
for(int k=0;k<n;++k){
cnt++;
}
}
}O(n)
O(n)*O(n) = O(n²)
直接看範例
int main(){
int cnt = 0;
for(int i=0;i<n;++i){
cnt++;
}
for(int i=0;i<n;++i){
for(int k=0;k<n;++k){
cnt++;
}
}
for(int i=1;i<n;i<<=1){
for(int k=0;k<n;++k){
cnt++;
}
}
}O(n)
O(n)*O(n) = O(n²)
O(n)*O(log₂n) = O(nlog₂n)
直接看範例
int main(){
int cnt = 0;
for(int i=0;i<n;++i){
cnt++;
}
for(int i=0;i<n;++i){
for(int k=0;k<n;++k){
cnt++;
}
}
for(int i=1;i<n;i<<=1){
for(int k=0;k<n;++k){
cnt++;
}
}
}O(n)
O(n)*O(n) = O(n²)
O(n)*O(log₂n) = O(nlog₂n)
O(n) + O(n²)+ O(nlog₂n) = O(n²)
題目測資 -> 時間複雜度 ->猜演算法
小技巧 :
分析排序演算法
的時間複雜度
泡沫排序法
Bubble sort
倆倆比較相鄰元素,如果右大於左就交換
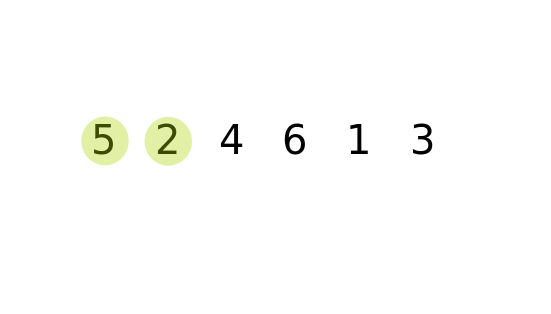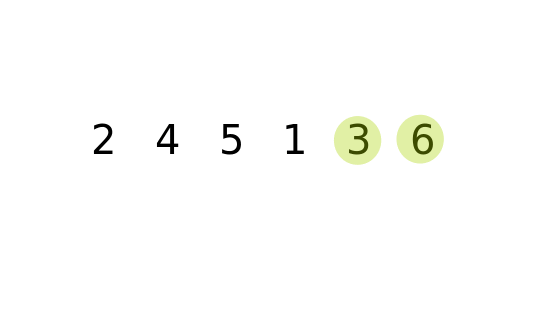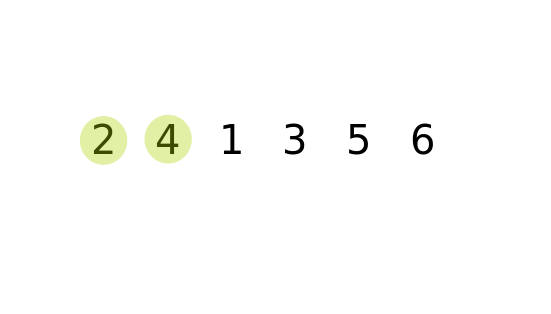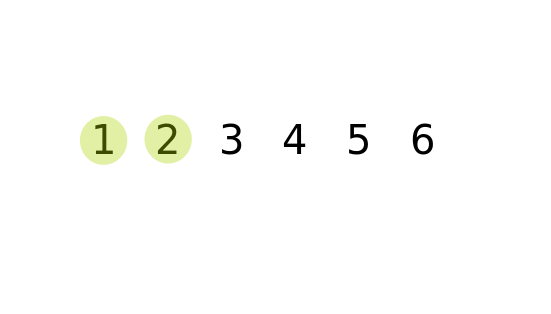
- 每次比較(交換)相鄰元素 :O(1)
- 比較一輪 : O(N)
- 比較N輪 : O(N^2)
總時間複雜度 : O(N^2)
插入排序法
Insertion sort
假設前 i 個元素已排序過的,把第 i+1 的元素排入前 i 個元素中
將新元素排入已排序過的數列
O(n)
從頭到尾將每個元素排入
O(n) * O(n) = O(n²)
總時間複雜度 : O(n²)
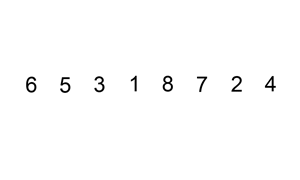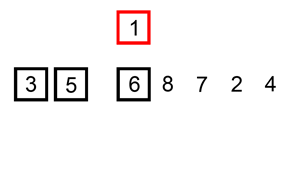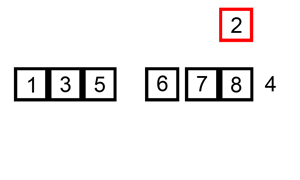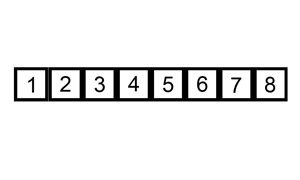
合併排序法
Merge sort
先倆兩排,再四四排,......,不斷把已排序過的合併
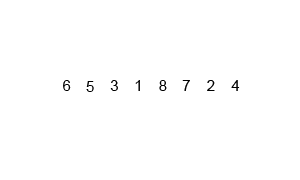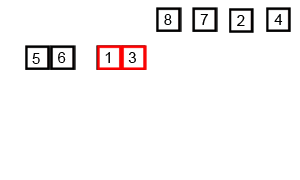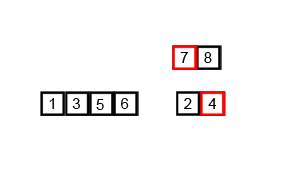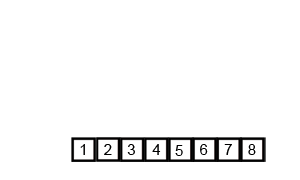
每次將個已排序過的合併
O(n)
每次合併好的長度是原本的兩倍
->合併的次數是 log₂n
O(log₂n)
總時間複雜度 ?
好像怪怪的 ?
遞迴複雜度
我們可以將merge sort的複雜度寫成以下式子
T(n) = 2T(n/2) + n
排序好長度為n的操作次數
來數數看操作次數
需要先合併好兩個長度為 n/2 的陣列
將兩個已排序的陣列合併
大約n次操作
T(1) = 1
O(n) = ?
n
n/2
n/2
n/4
n/4
n/4
n/4
.........
.........
.........
.........
.........
.........
.........
.........
1
1
1
1
1
1
1
1
好麻煩,那不是每次都要畫出來看嗎?
好麻煩,那不是每次都要畫出來看嗎?
先看看幾個常見的就好
好麻煩,那不是每次都要畫出來看嗎?
先看看幾個常見的就好

以後來電研上課就教更酷的方法 XXD
快速排序法
Quick sort
隨便抓一個元素當作標準,把大於它的丟右邊,小於它的丟左邊
繼續在左右做同樣的事情

Quick sort 複雜度
每次將元素分成左右兩邊 -> O(n)
Quick sort 複雜度
最差情況 :
每次選到的元素都是當前範圍最小/大,要做n次
-> O(n²)
每次將元素分成左右兩邊 -> O(n)
Quick sort 複雜度
每次將元素分成左右兩邊 -> O(n)
最佳情況 :
每次選到的元素都是當前範圍的中位數,把陣列切成等長的兩份
要做log₂n次 -> O(nlogn)
Quick sort 複雜度
每次將元素分成左右兩邊 -> O(n)
平均情況 :
雖然不一定均勻分成兩份,但遞迴樹的高度大約還是log₂n
期望複雜度 : O(nlogn)
還能在更快嗎 ?
還能在更快嗎 ?
基於比較的sort algo已經被證明複雜度下限為O(nlog₂n)
如果不要比較呢 ?
還能在更快嗎 ?
基於比較的sort algo已經被證明複雜度下限為O(nlog₂n)
如果不要比較呢 ?
基數排序法
Radix sort

放一輪 O(n),要放k次,總時間複雜度為 O(nk)
(k為最大的位數數量)
既然這個方法那麼快,它就要付出代價 !!
只能排序整數 QQ
最後介紹一個雖然不太實用,但很有趣的排序法
有沒有一種排序法,不須比較、交換、或是剛剛的分類(放籃子)
最後介紹一個雖然不太實用,但很有趣的排序法
有沒有一種排序法,不須比較、交換、或是剛剛的分類(放籃子)
睡覺排序法
sleep sort
最後介紹一個雖然不太實用,但很有趣的排序法
有沒有一種排序法,不須比較、交換、或是剛剛的分類(放籃子)
睡覺排序法
sleep sort
複雜度呢 ??
最後介紹一個雖然不太實用,但很有趣的排序法
有沒有一種排序法,不須比較、交換、或是剛剛的分類(放籃子)
睡覺排序法
sleep sort
複雜度呢 ??
似乎沒有什麼討論的意義
講了那麼多,難道排序那麼麻煩,還要自己寫 ?
講了那麼多,難道排序那麼麻煩,還要自己寫 ?
std::sort
int main(){
vector<int> arr1;
int arr2[10000000];
sort(arr1.begin(),arr1.end());
sort(arr2,arr2+10000000);
}
stable sort
穩定排序
、
自定義排序
stable sort
穩定排序
stable sort
穩定排序
不會把相同數字大小的元素打亂
stable sort
穩定排序
不會把相同數字大小的元素打亂
ex:
4 8 7 5 7 1 0 2 1
stable sort
穩定排序
不會把相同數字大小的元素打亂
ex:
4 8 7 5 7 1 0 2 1
stable sort
穩定排序
不會把相同數字大小的元素打亂
ex:
4 8 7 5 7 1 0 2 1
stable sort
穩定排序
不會把相同數字大小的元素打亂
ex:
4 8 7 5 7 1 0 2 1
0 1 1 2 4 5 7 7 8
自定義排序
自定義排序
就是看你想怎麼排,就怎麼排!
自定義排序
就是看你想怎麼排,就怎麼排!
像是從大排到小、用比值排(可能元素有兩個變數)..等
#include<bits/stdc++.h>
using namespace std;
struct object{
int a,b,c,d,e;
};
bool comp1(object x,object y){
return y.a > x.a;
}
bool comp2(object x,object y){
return y.a < x.a;
}
bool comp3(object x,object y){
return y.a * y.b > x.a * x.b;
}
bool comp4(object x,object y){
return y.d * x.c > x.d * y.c;
}
int main() {
vector<object> p;
sort(p.begin(),p.end(),comp1);
}有什麼用???
假設一個東西有多種性質
ex
一個食物有健康度、好吃度、價錢等
假設一個東西有多種性質
ex
一個食物有健康度、好吃度、價錢等
小美是個很正又有錢的正妹
假設一個東西有多種性質
ex
一個食物有健康度、好吃度、價錢等
小美是個很正又有錢的正妹
多正 ?
假設一個東西有多種性質
ex
一個食物有健康度、好吃度、價錢等
小美是個很正又有錢的正妹
多正 ? 身高100公分 體重100公斤
假設一個東西有多種性質
ex
一個食物有健康度、好吃度、價錢等
小美是個很正又有錢的正妹
多正 ? 身高100公分 體重100公斤
因此我們可以知道牠吃東西時
假設一個東西有多種性質
ex
一個食物有健康度、好吃度、價錢等
小美是個很正又有錢的正妹
多正 ? 身高100公分 體重100公斤
因此我們可以知道牠吃東西時
一定是優先看好吃度,再來是看價錢,最後才是健康度
現在有很多食物,要如何依照小美的喜好程度排序呢?
現在有很多食物,要如何依照小美的喜好程度排序呢?
依順序由健康度、價錢、好吃度做三次排序
方法一
現在有很多食物,要如何依照小美的喜好程度排序呢?
方法一
直接寫在自定義比較函式中
現在有很多食物,要如何依照小美的喜好程度排序呢?
依順序由健康度、價錢、好吃度做三次排序
穩定排序 !
方法二
蛤?
蛤?
可以感性理解 :
蛤?
可以感性理解 :
較晚排序會把較早的排序打亂
蛤?
可以感性理解 :
較晚排序會把較早的排序打亂
因此優先度較高的要比較晚排序
練習看看與排序有關的題目八
但其實排序大部分會是其他演算法的其中一步
二分搜
小名有很多相同的籃球,他聽老闆說他賣的籃球很硬,不會爆,
好奇的小名決定要測試籃球,可以被他多重的拳頭打,才會破掉,但是平常有在健身的小名,渾身肌肉,最用力的拳,重達
100000000000000000000牛頓
先看個題目
小名有很多相同的籃球,他聽老闆說他賣的籃球很硬,不會爆,
好奇的小名決定要測試籃球,可以被他多重的拳頭打,才會破掉,但是平常有在健身的小名,渾身肌肉,最用力的拳,重達
100000000000000000000牛頓
小名已經測試了好幾百年還是沒測出來,請幫幫小明吧 !
先看個題目
小名有很多相同的籃球,他聽老闆說他賣的籃球很硬,不會爆,
好奇的小名決定要測試籃球,可以被他多重的拳頭打,才會破掉,但是平常有在健身的小名,渾身肌肉,最用力的拳,重達
100000000000000000000牛頓
小名已經測試了好幾百年還是沒測出來,請幫幫小明吧 !
先看個題目
以下簡稱100000000000000000000為n,有點長
小明的方法 :
一牛頓一牛頓慢慢往上試,
是到第一次破掉就是答案!!!
小明的方法 :
一牛頓一牛頓慢慢往上試,
是到第一次破掉就是答案!!!
可惜等到人類滅絕也測不出來QQ
比較聰明的方法一
用跳的測 !!!
比較聰明的方法一
用跳的測 !!!
想像有一個標記,如果2^i牛頓不會破,就把標記往上移2^i牛頓,
i 從 log₂n ~ 0
比較聰明的方法一
用跳的測 !!!
想像有一個標記,如果2^i牛頓不會破,就把標記往上移2^i牛頓,
i 從 log₂n ~ 0
試到 i = 0 後,標記在的位置就會是最後一個不會破的力 !!
標記的下一個就是答案拉 :)
比較聰明的方法一
用跳的測 !!!
想像有一個標記,如果2^i牛頓不會破,就把標記往上移2^i牛頓,
i 從 log₂n ~ 0
試到 i = 0 後,標記在的位置就會是最後一個不會破的力 !!
標記的下一個就是答案拉 :)
居然從本可能要打100000000000000000000拳變成
67拳內解決 !!!!
比較聰明的方法二
用猜數字遊戲的方法
比較聰明的方法二
用猜數字遊戲的方法
每次猜最中間的力量打,每次答案的可能就會減半
比較聰明的方法二
用猜數字遊戲的方法
每次猜最中間的力量打,每次答案的可能就會減半
也可以從本可能要打100000000000000000000拳變成
67拳內解決 !!!!
這兩個做法就是二分搜 !!
可以把二分搜想成要找到一個分界線
例如把前面的故事轉換成 1:破了 0:沒破
可以把二分搜想成要找到一個分界線
例如把前面的故事轉換成 1:破了 0:沒破
力道小
力道大
000000000.......0000000111111111....11111111
可以把二分搜想成要找到一個分界線
例如把前面的故事轉換成 1:破了 0:沒破
力道小
力道大
000000000.......0000000111111111....11111111
我們要找的就是那 01交界 !
用第二種方法示範 :
分此我們可以訂兩個標記
L 代表它左邊全是 0
R 代表它右邊全是 1
L ~ R 就是 ??? (下以X表示)
LXXXXXXXXXXXXXXR
LXXXXXXXXXXXXXXR
LXXXXXXX0XXXXXXR
00000000LXXXXXXR
00000000LXXX1XXR
00000000LXXXR111
00000000LX0XR111
0000000000LXR111
0000000000L1R111
0000000000LR1111
L 就是最後一個 0
R 就是最後一個 1
我們要找的是 01的交界處
因此查找的對象要有單調性喔
我們要找的是 01的交界處
因此查找的對象要有單調性喔
簡單來說就是像剛剛那樣
如果500牛頓不會破
那 1~499也一定不會破
我們要找的是 01的交界處
因此查找的對象要有單調性喔
簡單來說就是像剛剛那樣
如果500牛頓不會破
那 1~499也一定不會破
999999牛頓會破
那大於999999也一定破 !
如何實作 ?
1、用內建的
1、用內建的
lower_bound
找到第一個大於等於的位置
1、用內建的
lower_bound
找到第一個大於等於的位置
upper_bound
找到第一個大於的位置
要先排序 !!
不然會壞掉
自己實作
int l = -1, r = n, m;
while(l+1<r){
m = (l+r)/2;
if(f(m) >= tar) r = m;
else l = m;
}練習看看吧
給你n個數字和一個x,在n中找兩個數字,其和為x
印出其index,沒有的話印出IMPOSSIBLELE
假設現在我們已經有一個數字 a
假設現在我們已經有一個數字 a
如果x-a出現在那n個數中,我們就找到解了 !
假設現在我們已經有一個數字 a
如果x-a出現在那n個數中,我們就找到解了 !
假設現在我們已經有一個數字 a
如果x-a出現在那n個數中,我們就找到解了 !
把n個數字中的每一個當成a,找找看有沒有x-a
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define maxn 200005
pair<int,int> p[maxn];
int n,x;
main(){
cin>>n>>x;
for(int i=1;i<=n;++i){
cin>>p[i].first;
p[i].second = i;
}
sort(p+1,p+1+n);
for(int i=1;i<=n;++i){
if(p[i].first >= x) break;
int tar = x - p[i].first;
auto it = lower_bound(p+1,p+1+n,pair<int,int>{tar,0});
if(it!=p+1+n && it->first == tar && it->second != p[i].second){
cout<<p[i].second<<' '<<it->second<<endl;
return 0;
}
}
cout<<"IMPOSSIBLE"<<endl;
}複雜度 ?
複雜度 ?
排序 : O(nlogn)
複雜度 ?
排序 : O(nlogn)
掃過一遍 O(n) * 每次二分搜 O(logn)
複雜度 ?
排序 : O(nlogn)
掃過一遍 O(n) * 每次二分搜 O(logn)
O(nlogn) + O(nlogn) = O(nlogn)
練習看看不同的題型八
輸入一個n,問所有n*n的乘法表中,中位數是誰
n <= 1e6
練習看看不同的題型八
輸入一個n,問所有n*n的乘法表中,中位數是誰
n <= 1e6
發現居然可以2分搜 !!
1 2 3 4 5
2 4 6 8 10
3 6 9 12 15
4 8 12 16 20
5 10 15 20 25
1 2 3 4 5
2 4 6 8 10
3 6 9 12 15
4 8 12 16 20
5 10 15 20 25
如果我猜答案是 k ?
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n;
int cal(int x){
int sum = 0;
for(int i=1;i<=n;++i) sum += min(x/i,n);
return sum;
}
main(){
cin>>n;
if(n<=3){
cout<<n<<endl;
return 0;
}
int l = 1,r = n*n, m, tar = (n*n+1)/2;
while(l+1<r){
m = (l+r)/2;
if(cal(m)>=tar) r = m;
else l = m;
}
cout<<r<<endl;
return 0;
}
最多猜logn 次答案 O(logn)
複雜度 ?
最多猜logn 次答案 O(logn)
複雜度 ?
每次驗證猜得對不對花 O(n)
最多猜logn 次答案 O(logn)
複雜度 ?
每次驗證猜得對不對花 O(n)
O(logn) * O(n) = O(nlogn)
暑假太閒,可以去哪裡練習阿?
經典算法裸題大全,可以開刷了
資芽的OJ
暑訓
By maxbrucelen
暑訓
- 214



