Milo Viviani 
(joint work with prof. Michele Benzi)

Scuola Normale Superiore - Pisa

UMI23
Pisa, 04-09 September 2023

Motivation

Solution of (large) linear systems

• \(A\in\mathbb{M}_n(\mathbb{C})\) and \(x,b\in \mathbb{C}^n\)
• \(A\) is large non-Hermitian positive definite

Let \(A = H + S\), where \(H=\frac{A+A^*}{2}\) and \(S=\frac{A-A^*}{2}\)

HSS algorithm (Bai, Golub and Ng, 2003)

HSS algortihm

• Unconditionally convergent to the solution of \(Ax=b\), for any \(\alpha>0\)
• Upper bound of the contraction factor depends on \(\sigma(H)\) but not on \(\sigma(S)\)
• Optimal \(\alpha\) is given by \(\alpha_{opt}:=\sqrt{\lambda_{max}(H)\lambda_{min}(H)}\)
• The two-step iteration is solved via some CG + Krylov subspace method (IHSS)
• Efficient solver for saddle-point problems for discretized elliptic PDEs (Benzi, Gander and Golub, 2003)

Skew shifted HSS algortihm (Greif, 2022)

• \(J\) is the standard symplectic matrix
• Not unconditionally convergent to the solution of \(Ax=b\), but there is a critical value for \(\alpha\) depending on the eigenvalues of the skew-Hamiltonian matrix \(JS\)

or

(1)

(2)

Skew shifted HSS algortihm (Greif, 2022)

Rmk. The scheme (1) is equivalent to

which corresponds to the splitting of \(JA\) in the Hamiltonian and skew-Hamiltonian parts \(JH\) and \(JS\)

Rmk. Hermitian and skew-Hermitian and skew-Hamiltonian and Hamiltonian are of Jordan and Lie algebras pairs

Q. How the Lie-Jordan theory is linked to the HSS scheme? 

Lie and Jordan algebras

Def. A Lie algebra \(\mathfrak{g}\) is a vector space with a bilinear operator \([\cdot,\cdot]:\mathfrak{g}\times\mathfrak{g}\rightarrow\mathfrak{g}\), such that for all \(A,B,C\in\mathfrak{g}\):

• \([[A,B],C] + [[B,C],A] + [[C,A],B] = 0\) (Jacobi)
• \([A,B] = - [B,A] \)

Def. A Jordan algebra \((\mathbb{J},\circ)\) is a non-associative algebra over a field, such that for all \(A,B\in \mathbb{J}\):

• \(A\circ B = B\circ A\)
• \((A\circ B)\circ A^2 = A\circ ( B\circ A^2)\)

Es. \(\mathbb{M}_n(\mathbb{R})\) is both a Lie and Jordan algebra, w.r.t. to the commutator and anti-commutator

Lie-Jordan splitting

Key ingredient: any \(A\in\mathbb{M}_n(\mathbb{R})\) can be uniquely decomposed in a symmetric and a skew-symmetric part

\(\mathbb{M}_n(\mathbb{R})\cong\mathfrak{so}_n(\mathbb{R}) \oplus sym_n(\mathbb{R})\)

• \(\mathfrak{so}_n(\mathbb{R}) \) is a real Lie algebra w.r.t. the matrix commutator \([A,B]=AB-BA\)
• \(sym_n(\mathbb{R})\) is a real Jordan algebra w.r.t. the matrix anticommutator \( A\circ B = AB+BA\)
• The splitting above is known as the Polar decomposition at the algebra level or the Cartan decomposition w.r.t. the involution \(\cdot^T\)

Lie-Jordan splitting

More generally, given any \(J\in\mathbb{M}_n(\mathbb{R})\) invertible symmetric or skew-symmetric, we get a pair of quadratic Lie and Jordan algebras

where
\(\mathfrak{g}_J:=\lbrace A\in\mathbb{M}_n(\mathbb{R})\) such that \(A^TJ + JA=0\rbrace\)

\(\mathbb{J}:=\lbrace A\in\mathbb{M}_n(\mathbb{R})\) such that \(A^TJ - JA=0\rbrace\)

\(\mathbb{M}_n(\mathbb{R})\cong\mathfrak{g}_J \oplus_S \mathbb{J}\)

• The splitting is orthogonal w.r.t.: \(<A,B>_S :=Tr(A^TSB)\), where \(S=JJ^T\)

J-HSS scheme 

Let \(A = H + S\), where \(H=\frac{J^{-1}(A^TJ+JA)}{2}\) and \(S=\frac{J^{-1}(A^TJ-JA)}{2}\)

Thm.

• Let \(J\) be symmetric. Then, the scheme above converges toward the solution of \(Ax=b\) if \(max_{\lambda\in\sigma(JH)}|\frac{\alpha-\lambda}{\alpha + \lambda}|<1\)
• Let \(J\) be skew-symmetric. Then, the scheme above converges toward the solution of \(Ax=b\) if \(max_{\lambda\in\sigma(JS)}|\frac{\alpha-\lambda}{\alpha + \lambda}|<1\)

J-HSS scheme 

• By the Sylvester's inertia theorem, when \(J\) is congruent to a diagonal matrix with zeros and \(\pm 1\) equal to the rank of \(J\), whereas when J is skew is a block diagonal with zeros and symplectic blocks equal to half the rank of \(J\). Hence, in this case the Lie algebra g is isomorphic to \(\mathfrak{u}(p,q)\) or \(\mathfrak{sp}(n)\).
• \(J\) neither symmetric or skew can be reconducted to the previous case
• Considering \(JAx=Jb\), brings us to the classical HSS scheme

Q. Are there Lie-Jordan splitting not isomorphic to the Hermitian and skew-Hermitian one?

Formally real Jordan algebras

In 1934, Jordan, Von Neumann and Wigner classified the simple formally real Jordan algebras, i.e. real Jordan algebras such that:

if \(A_1^2+A_2^2+...+A_n^2=0\), then \(A_1=A_2=...=A_n=0\)

They are of three kinds:

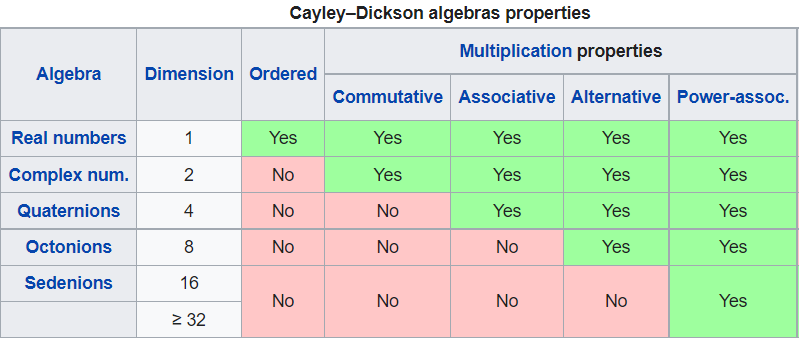
1. Hermitian matrices for any \(n\geq 1\) with coefficients in \(\mathbb{R},\mathbb{C},\mathbb{H}\)
2. \(JSpin_n\): \(\mathbb{R}\textbf{1}\oplus\mathbb{R}^n\) with \((a\textbf{1},\textbf{v})\circ(b\textbf{1},\textbf{w})=((ab+<\textbf{v},\textbf{w}>)\textbf{1},a\textbf{v}+b\textbf{w})\)
3. Hermitian matrices for \(n=3\) with coefficients in \(\mathbb{O}\) [Albert algebra]

Rmk.

• \(JSpin_n\) can be embedded in \(sym_{2^n}(\mathbb{R})\)
• The Albert algebra is the only formally real exceptional algebra, since it cannot be embedded in a associative algebra

Formally real Jordan algebras

• The Hermitian and skew-Hermitian splitting and the relative HSS scheme can be extended to matrix with coefficients in \(\mathbb{R},\mathbb{C},\mathbb{H}\)
   
• \(\mathbb{M}_n(\mathbb{H})\cong\mathbb{M}_{2n}(\mathbb{C})\), hence all the analysis for quaternionic matrices can be performed using complex matrices
   
• A \(JSpin_n\) Jordan algebra has a Lie algebra complement \(\mathfrak{g}\subset\mathfrak{so}(2^n)\)
   
• The Albert algebra is not clearly treatable, since it cannot be represented via real or complex matrix calculus

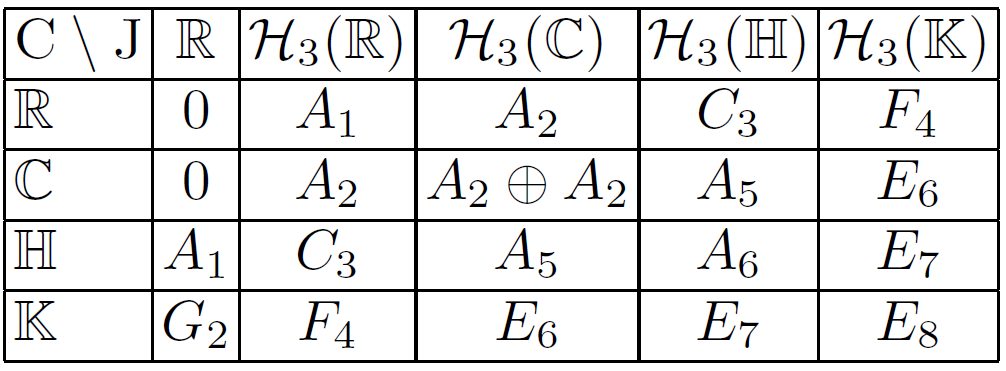
Freudenthal-Tits magic square

• Another way to associate a Lie algebra to a Jordan algebra \(\mathbb{J}\) is to define the structure algebra \(str(\mathbb{J})=\mathbb{J}\oplus Der(\mathbb{J})\).
  Es. \(\mathbb{J}=sym_n(\mathbb{R})\) has \(Der(\mathbb{J})\cong\mathfrak{so}(n)\) and \(str(\mathbb{J})\cong\mathbb{M}_n(\mathbb{R})\)
   
• The Freudenthal-Tits construction \(FT (C, J) := Der(C)⊕(C0⊗J0)⊕Der(J)\) links \(3\times 3\) Hermitian matrices to semisimple Lie algebras

Conclusions and future work

• The HSS scheme can be directly extended to J-quadratic Lie and Jordan algebras
• The HSS scheme works for Hermitian matrices with coefficients in \(\mathbb{R},\mathbb{C},\mathbb{H}\)
• Is there any case in which is convenient to consider the \(JSpin_n\) structure and its Lie algebra complement?
• The exceptional cases emerge while considering octonions, but only for dimension 3, which makes the interest for iterative schemes purely academic
• Extend the analysis of the HSS algorithm for any real Jordan algebra of matrices, considering the structure algebra \(str(\mathbb{J})=\mathbb{J}\oplus Der(\mathbb{J})\)