Milo Viviani 
(joint work with prof. Klas Modin and Paolo Cifani)

Scuola Normale Superiore - Pisa

Geometric methods and stochastic reduction
for fluid models
Enschede, 08-12 May 2023

Motivations

2D Euler equations

Ergodic hypotesis: for \(T\) large and a functional \(\phi\)

for some invariant measure \(\mu\) on \(H\) Hilbert space

Motivations

Invariant measures

• Enstrophy measure: \(\nu(d\omega)\approx e^{-E(\omega)}d\omega\)
  More precisely, centered Gaussian measure on \(H^{-1-}=\cap_{\varepsilon>0}H^{-1-\varepsilon}\)
   
• We would like to take \(\mu_{\alpha,k}(d\omega)\approx e^{-\alpha C_k(\omega)}\nu(d\omega)\), for some Casimir \(C_k(\omega)=\int_S\omega^kdS\)
   
• Higher Casimir invariant measures: open problem!
   
• Can we study an analogue problem for a finite dimensional system? YES!

Zeitlin model

• \(W\in\mathfrak{su}(N)\)
• Enstrophy measure \(\nu(dW)=e^{-Tr(W^*W)}dW\)
• Higher Casimir measures
  \(\mu_{\alpha,\beta,k}(dW)=e^{-\alpha Tr(W^*W)-\beta Tr((W^*W)^k)}dW\)
• \(\mu\) well defined for any \(k\geq 1\)

Given some 

\(\mu_{\alpha,\beta,k}(dW)=e^{-\alpha Tr(W^*W)-\beta Tr((W^*W)^k)}dW\)

we would like to generate \(W_0\) random matrix whose Law is \(\mu\)

A possible technique to generate such \(W_0\) is Metropolis-Hastings algorithm

Metropolis-Hastings

1. Let \(W_0\in\mathfrak{su}(N)\) be given
2. Pick \(\Delta W\in\mathfrak{su}(N)\) generated by a distribution \(p\) on \(\mathfrak{su}(N)\)
3. Let define \(\delta:=V(W_0+\Delta W)-V(W_0)\)
4. Define \(W_0:=W_0+\Delta W\) with probability \(e^{-(\delta\wedge 0)}\)
5. Repeat from 1 until \(V\) becomes stationary

Generate \(W\) distributed according to
\(\mu(dW)=e^{-V(W)}dW\), \(V\geq 0\)

Metropolis-Hastings

• This approach has not be fruitful
   
• Apparently not much changed varying the parameters \(\alpha,\beta,k\)
   
• Not clear the influence of the higher Casimirs

 \(V(W)=\alpha Tr(W^*W)-\beta Tr((W^*W)^k)\),
for some \(\alpha,\beta,k\)

Alternative approach

• Let us consider \(W=W(t)\) solution of Euler-Zeitlin equations
   
• \(W(t) = U(t)^*W_0 U(t)\), \(U(t)\) unitary for all \(t\geq 0\)
   
• Can we say something of \(U(\infty):=\lim_{t\rightarrow\infty}U(t)\)?
   
• It turns out that typically \(\sigma(U(\infty))\sim Unif(\mathbb{S}^1)\) and possibly \(U(\infty))\sim Haar(SU(N))\)

Haar generated \(U\)

\(Re(U)\)

\(eig(U)\)

 \(U(\infty)\)

\(eig(U)\)

\(Re(U)\)

Haar measure on \(SU(N)\)

• Unique probability measure on the Borel sets of \(SU(N)\) invariant with respect to left and right multiplication of \(U\in SU(N)\)
• Thm[Eaton, 1983]. If \(Z\in GL(N,\mathbb{C})\) has entries i.i.d. standard complex normal random variables, then applying the Gram-Schmidt orthonormalization to the columns of \(Z\), gives a unitary matrix \(Q\) is distributed with Haar measure.

Haar measure on \(SU(N)\)

• Gram-Schmidt algorithm is numerically unstable
• QR decomposition does not provide a unique Q and in general not distributed as Haar (Edelman and Rao, 2005)
   
• Mezzadri, 2007 provides a stable algorithm:
  - QR decomposition of \(Z=QR\) with entries i.i.d. normally distributed on \(\mathbb{C}\)
  - Define \(Q':=Q\Lambda\), where \(\Lambda:=diag(R)/|diag(R)|\), which is distributed as Haar

A first test

• Take some non-zero \(W_0\in\mathfrak{su}(N)\)
   
• Generate \(U\sim Haar(SU(N))\) with the Mezzadri algorithm
   
• Define \(W_{end}:=U^*W_0U\)
   

What do we get?

A first test

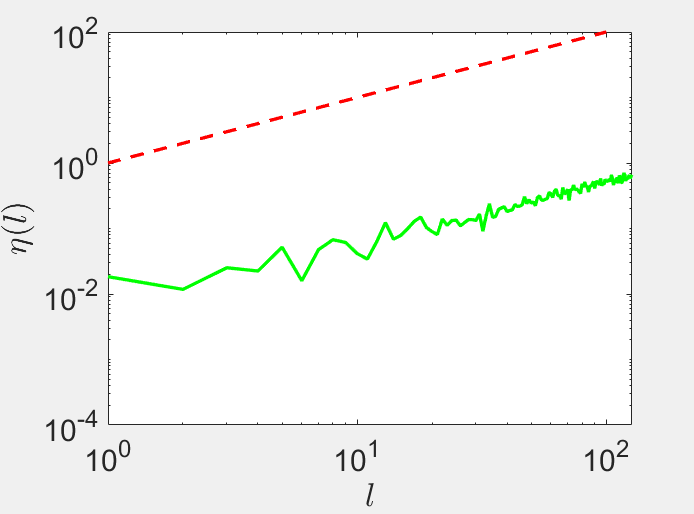
Enstrophy spectrum \(\approx l^1\)

A first test

• Conjecture: \(U\sim Haar(SU(N))\) if and only if \(Ad^*_U(W_0)\sim \nu(SU(N))\), for almost any \(W_0\in\mathfrak{su}(N)\), where \(\nu\) is the enstrophy measure.
• The unitary matrix \(U(\infty)\) not clearly distributed as Haar, in particular \(Ad^*_{U(\infty)}(W_0)\) is not distributed as \(\nu\)
• We need to add some constraint to the transformation \(U\). In particular, we want to retain energy and angular momentum

Metropolis-Hastings on \(SU(N)\)

1. Let \(W_0\in\mathfrak{su}(N)\) be given
2. Generate \(U\sim Haar(SU(N)\)
3. Resize \(U\): \(\hat U:=Cay(r CayInv(U))\), for some \(r<<1\)
4. \(W_{new}:=\hat{U}^*W_0\hat U\)
5. Let define \(\delta:=V(W_0+\Delta W)-V(W_0)\),
   for \(V(W)=\alpha(H(W)-H_0)^2+\beta(M(W)-M_0)^2\)
6. Define \(W_0:=W_0+\Delta W\) with probability \(e^{-(\delta\wedge 0)}\)
7. Repeat from 1 until \(V\) becomes stationary

Generate \(W\) distributed according to
\(\mu(dW)=e^{-\alpha(H(W)-H_0)^2-\beta(M(W)-M_0)^2}dW\),

via a random walk on \(SU(N)\)

Metropolis-Hastings on \(SU(N)\)

1. Let \(W_0\in\mathfrak{su}(N)\) be given
2. Generate \(\Xi\sim Unif(\mathbb{S}_{SU(N)})\)
3. Generate \(U:=Cay(r \Xi\)), for some \(r<<1\)
4. \(W_{new}:=U^*W_0 U\)
5. Let define \(\delta:=V(W_0+\Delta W)-V(W_0)\),
   for \(V(W)=\alpha(H(W)-H_0)^2+\beta(M(W)-M_0)^2\)
6. Define \(W_0:=W_0+\Delta W\) with probability \(e^{-(\delta\wedge 0)}\)
7. Repeat from 1.

Generate \(W\) distributed according to
\(\mu(dW)=e^{-\alpha(H(W)-H_0)^2-\beta(M(W)-M_0)^2}dW\),

via a random walk on \(SU(N)\)

Numerical test

Enstrophy spectrum: red vorticity transformed with Haar unitary matrix, green final spectrum, black evolving spectrum of \(W\) according to Metropolis

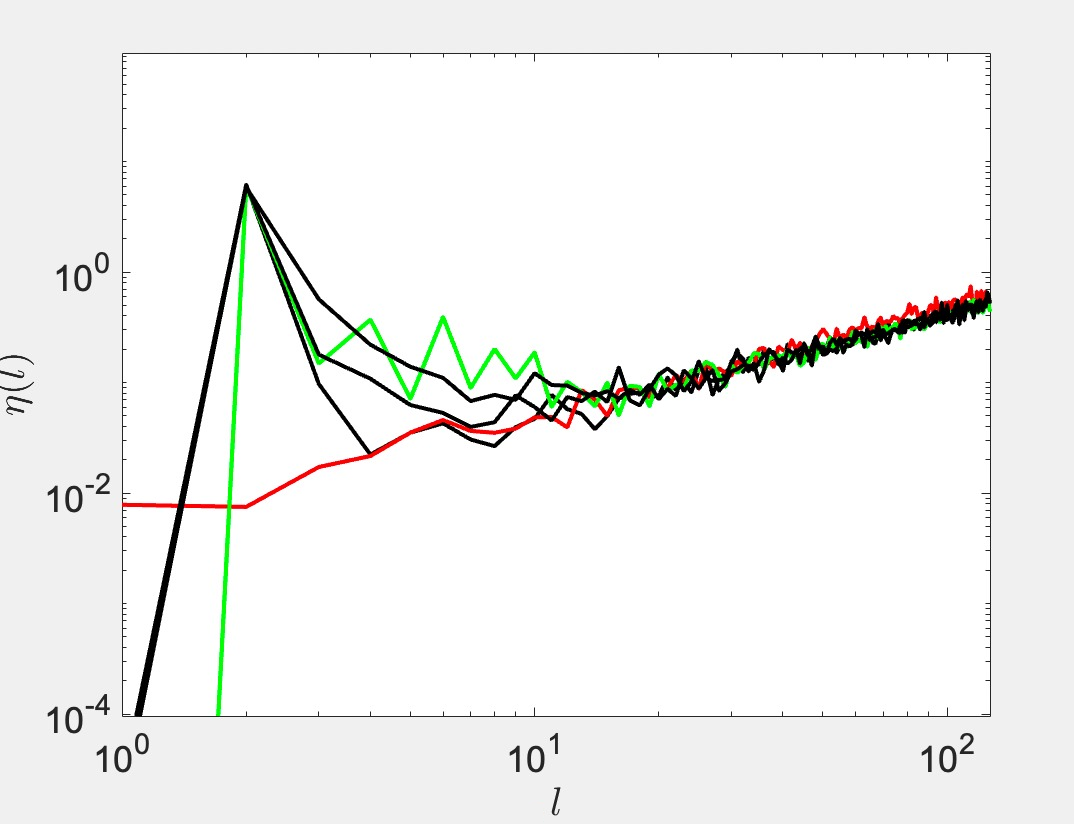
Numerical test

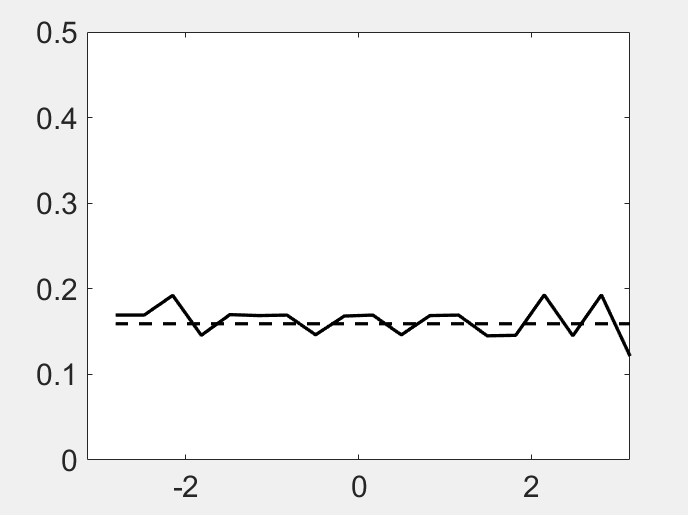
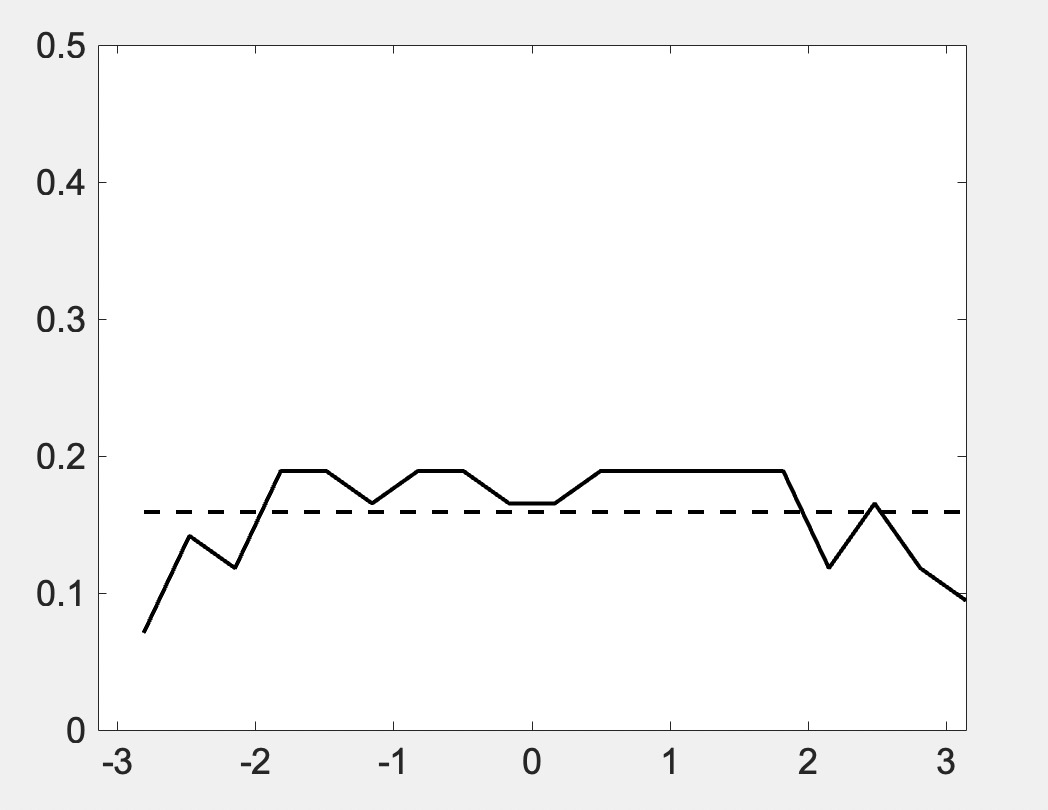
\(eig(U(\infty))\)

• The enstrophy distributes according to the power law \(l^1\) up to the smallest possible wavenumber \(l=2\)
   
• Therefore, either the random walk does not replicate correctly the Euler-Zeitlin statistics or it is much faster
   
• We propose to add information on the scale separation adding to \(V\) the term
  \(-\alpha_s (H(W_s)-H(W_0))^2\)

Numerical test

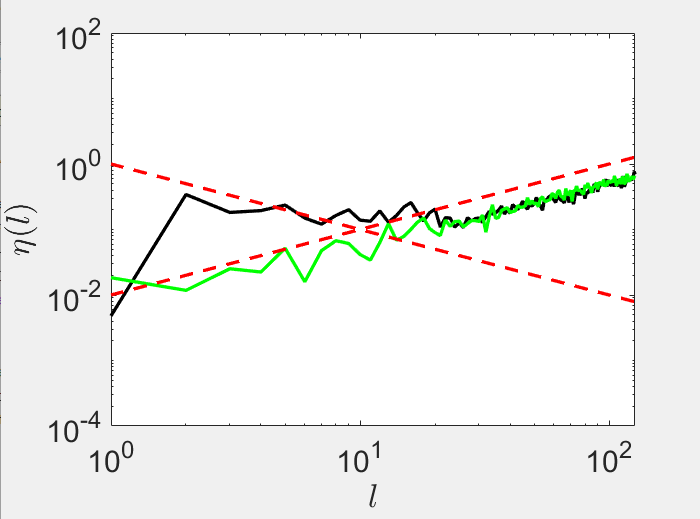
Enstrophy spectrum: red vorticity transformed with Haar unitary matrix, green final spectrum, black spectrum of \(W(\infty)\) generated with Metropolis

Numerical test

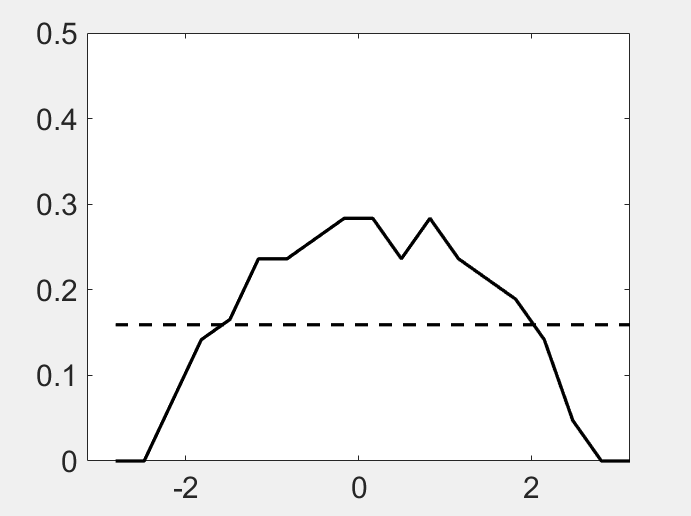
\(eig(U(\infty))\)

Conclusions

• We have shown that some statistics of Euler-Zeitlin can be recover via simulating a random walk on \(SU(N)\)
   
• Different interpretations of the results
   
• Need for more theoretical insight
   
• ...

Dank u voor uw aandacht...