Contact Estimation from External Joint Torque Measurements on a serial robotic arm
\newcommand{\rv}[1]{\mathsfit{#1}}
\newcommand{\rvv}[1]{\bm{\mathsfit{#1}}}
Tao Pang, Jack Umenberger and Russ Tedrake
Robot Locomotion Group
{pangtao, ju, russt}@csail.mit.edu
Motivation
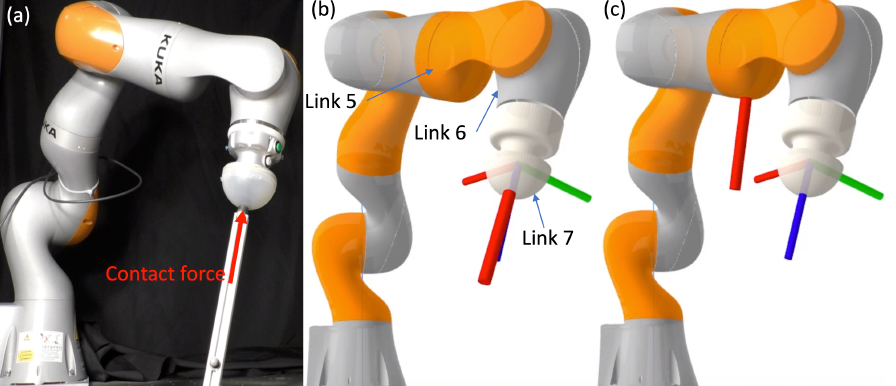
estimated contact force
- Robot arms such as KUKA IIWA and FRANKA PANDA can estimate \(\tau_{\text{ext}}\) using the generalized momentum observer.
- Assuming there is one external, point-contact force, existing methods can estimate \(\bm{p}_C\) and \(\bm{f}_C\) from \(\tau_{\text{ext}}\).
- However, some \(\tau_{\text{ext}}\) can be explained equally well by multiple contact points.
Haddadin, Sami, Alessandro De Luca, and Alin Albu-Schäffer. "Robot collisions: A survey on detection, isolation, and identification." IEEE Transactions on Robotics 33.6 (2017): 1292-1312.
Manuelli, L. and Tedrake, R., 2016, October. Localizing external contact using proprioceptive sensors: The contact particle filter. In 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (pp. 5062-5069).
- Existing methods do not take into account multiple solutions.
- The method by Haddadin et al. returns a contact point on the last link with non-zero torque measurement.
- Contact Particle Filter by Manuelli and Tedrake can return either one of the solutions.
- Goal: estimating from only external torque \(\tau_{\text{ext}}\)
- \(\bm{p}_C \in \mathcal{S}\): contact point C on the robot's surface \(\mathcal{S}\).
- \(\bm{f}_C \in \mathbb{R}^3\): contact force at point C.
M(q)\ddot{q} + C(q, \dot{q}) + \tau_g = \tau_{\text{m}} + \tau_{\text{ext}}
motor torque.
external torque due to contact
gravitational torque.
joint angles.
Coriolis.
Mathematically...
- We would like to solve
for the contact position \(\bm{p}_C\) and contact force \(\bm{f}_C\), subject to
- \(\bm{p}_C \in \mathcal{S}\): point C is on the robot's surface.
- \(\bm{f}_C \in \mathcal{K}_C\): force \(\bm{f}_C\) is inside the friction cone at C.
\bm{\tau}_\text{ext} = \bm{J}_C(\bm{q}, \bm{p}_C)^\intercal \bm{f}_C,
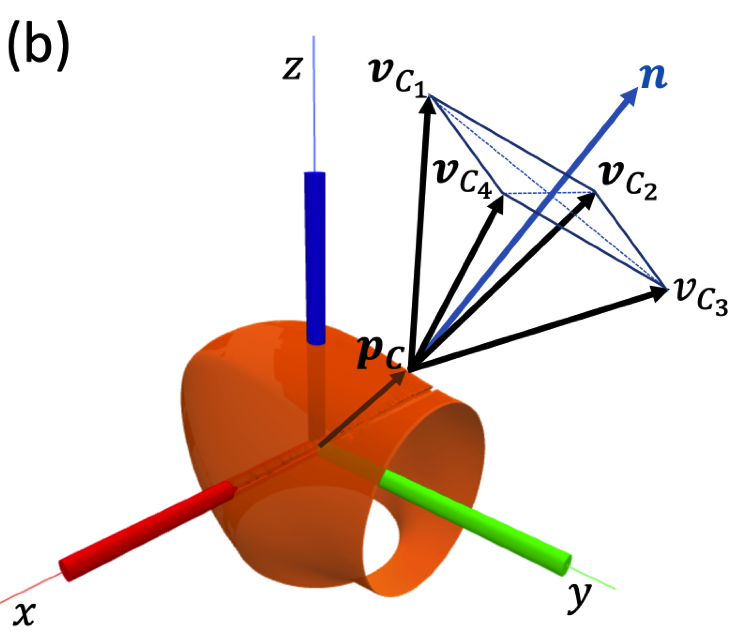
- This is equivalent to solving
\underset{\bm{\beta} \geq 0, \; \bar{\bm{p}}_C \in \mathcal{S}}{\text{min.}} \; \| \bm{J}(\bm{q}, \bar{\bm{p}}_C)^{\intercal} \bm{\beta} - \bm{\tau}_\text{ext} \|^2.
- The minimum squared error of at a known point C can be obtained by solving a quadratic program (QP):
- Common assumptions:
- Only one external contact.
- Contacts create no moment about the contact point.
Components of \(\bm{f}_C\) along \(\bm{v}_{C_i}\).
Link 6 of IIWA.
- Finding all possible contact positions is the same as finding all global minima of
l(\cdot; \bm{q}, \bm{\tau}_\text{ext})
\newcommand{\tauE}{\bm{\tau}_{\text{ext}}}
\newcommand{\pCbar}{\bar{\bm{p}}_C}
l(\pCbar; \bm{q}, \tauE) \coloneqq \underset{\bm{\beta} \geq 0}{\text{min.}} \; \| \bm{J}(\bm{q}, \pCbar)^{\intercal} \bm{\beta} - \bm{\tau}_\text{ext} \|^2
The landscape of
on the robot's surface \(\mathcal{S}\)
l(\cdot; \bm{q}, \bm{\tau}_\text{ext})
- We propose an algorithm to find all local minima of
- Considering that torque measurements are noisy, knowing the local minima in addition to the global ones could actually be beneficial.
l(\cdot; \bm{q}, \bm{\tau}_\text{ext})
Find all local minima of \(l(\cdot; \bm{q}, \bm{\tau}_\text{ext})\) with Rejection Sampling
- Sample points on the robot's surface, take the points with \(l \leq \epsilon\).
- Rejection rate is 98% with \(\epsilon = 0.005\).
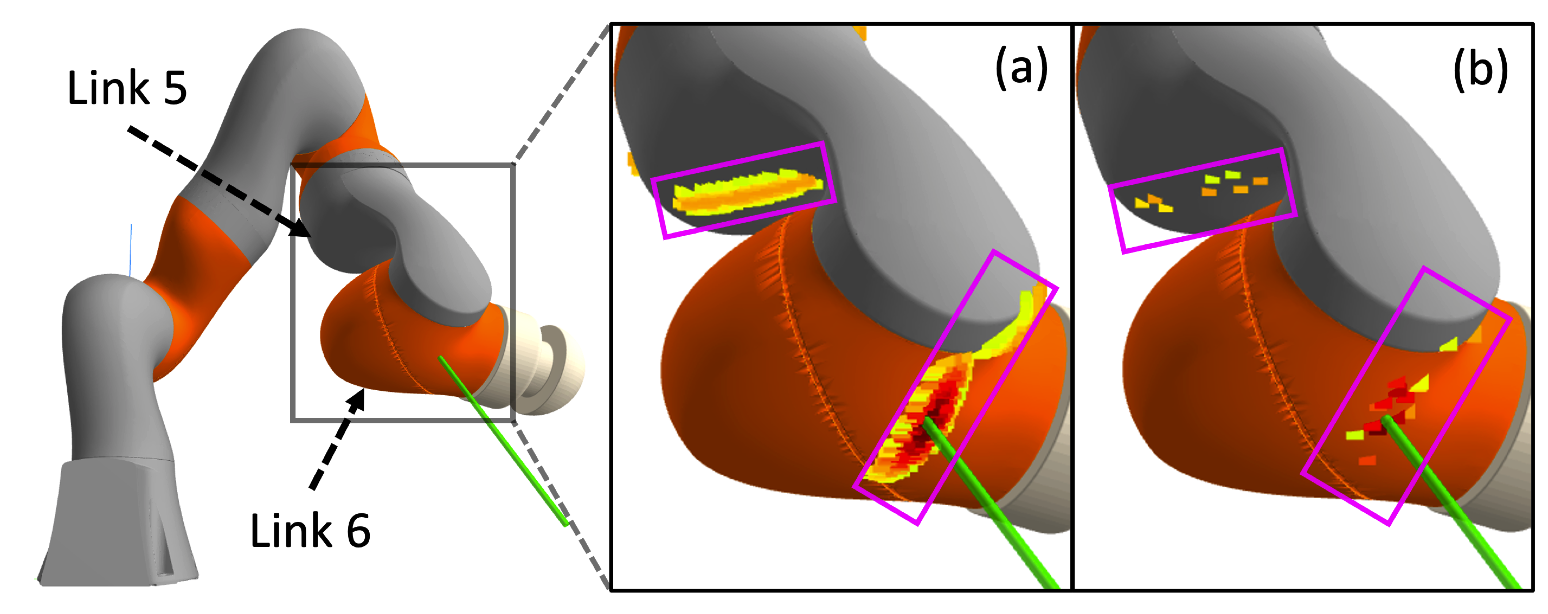
(a): accepted samples out of 10000 samples/link.
(b): accepted samples out of 500 samples/link.
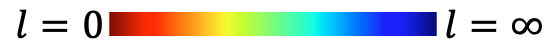
Find all local minima of \(l(\cdot; \bm{q}, \bm{\tau}_\text{ext})\) with Rejection Sampling + Gradient Descent (RSGD)
- Rejection sampling with a larger threshold \(\delta\).
- For example, acceptance rate rises to 17.5% with \(\delta = 0.1\)
- Run gradient descent on the accepted samples to converge to local minima of \(l(\cdot)\).
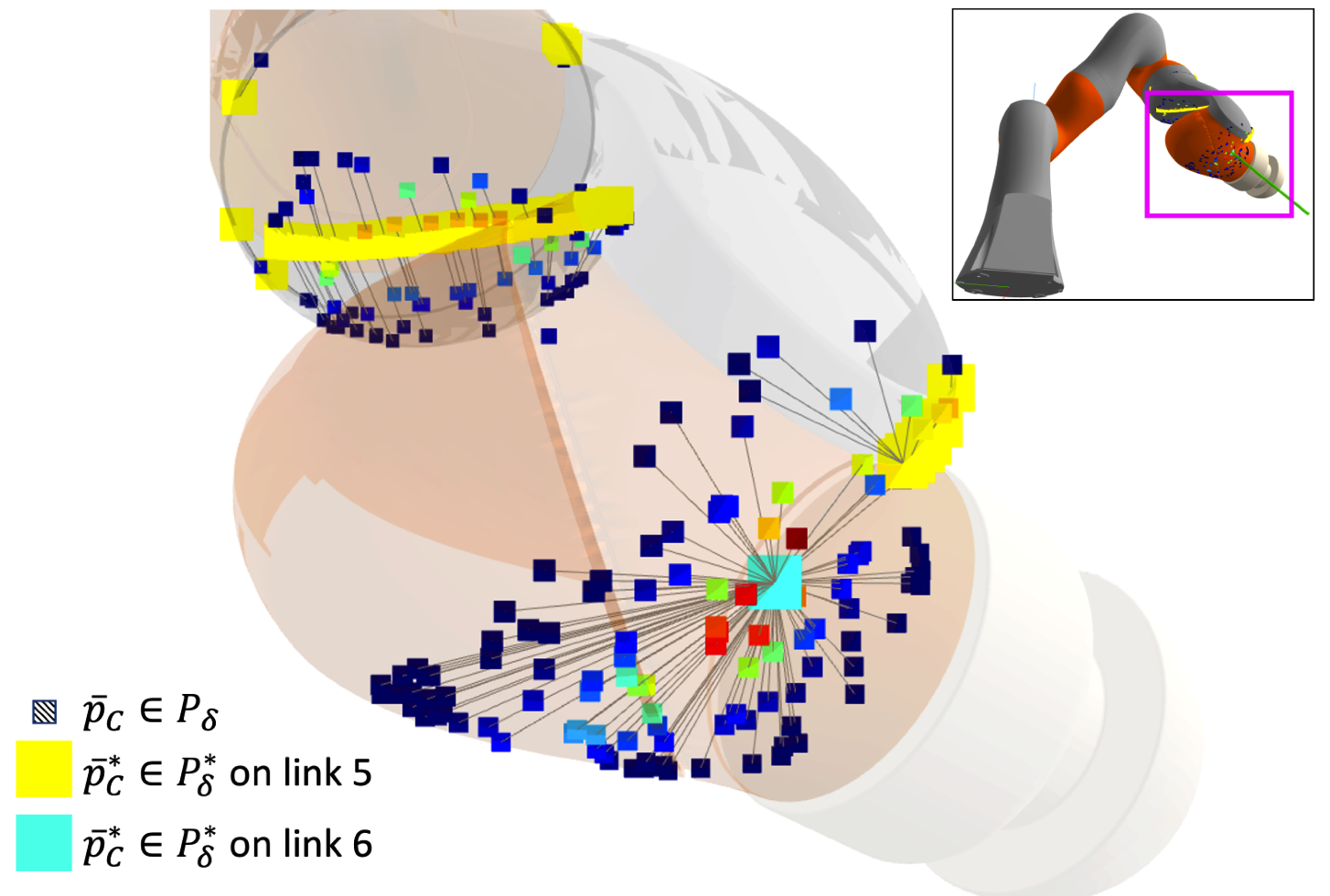
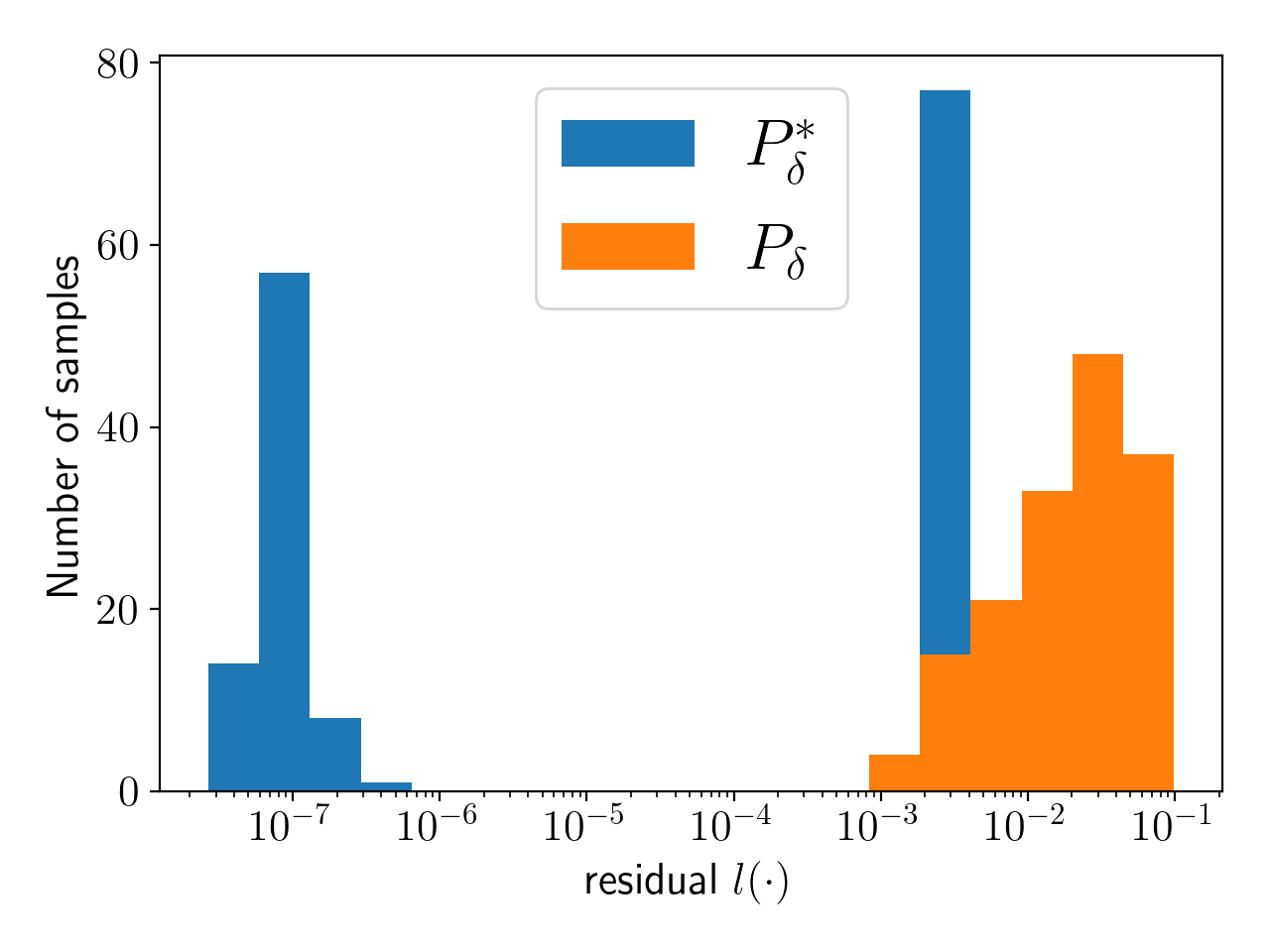
- \(P_\delta\): set of accepted samples.
- \(P_\delta^*\): set of optimized samples.
Find all local minima of \(l(\cdot; \bm{q}, \bm{\tau}_\text{ext})\) with Rejection Sampling + Gradient Descent (RSGD)
- \(P_\delta\): set of accepted samples.
- \(P_\delta^*\): set of optimized samples.
- Accepted / all samples: 172/1000
- Link 5 , converged_samples / accepted samples: 78/84
- Link 6 , converged_samples / accepted samples: 80/88
Works in other cases too! Runs at 10Hz on average.
Active Contact Discrimination
- Disambiguate candidate contact positions found by Rejection Sampling + Gradient Descent by making small motions.
Active Contact Discrimination
- Disambiguate candidate contact positions found by Rejection Sampling + Gradient Descent.
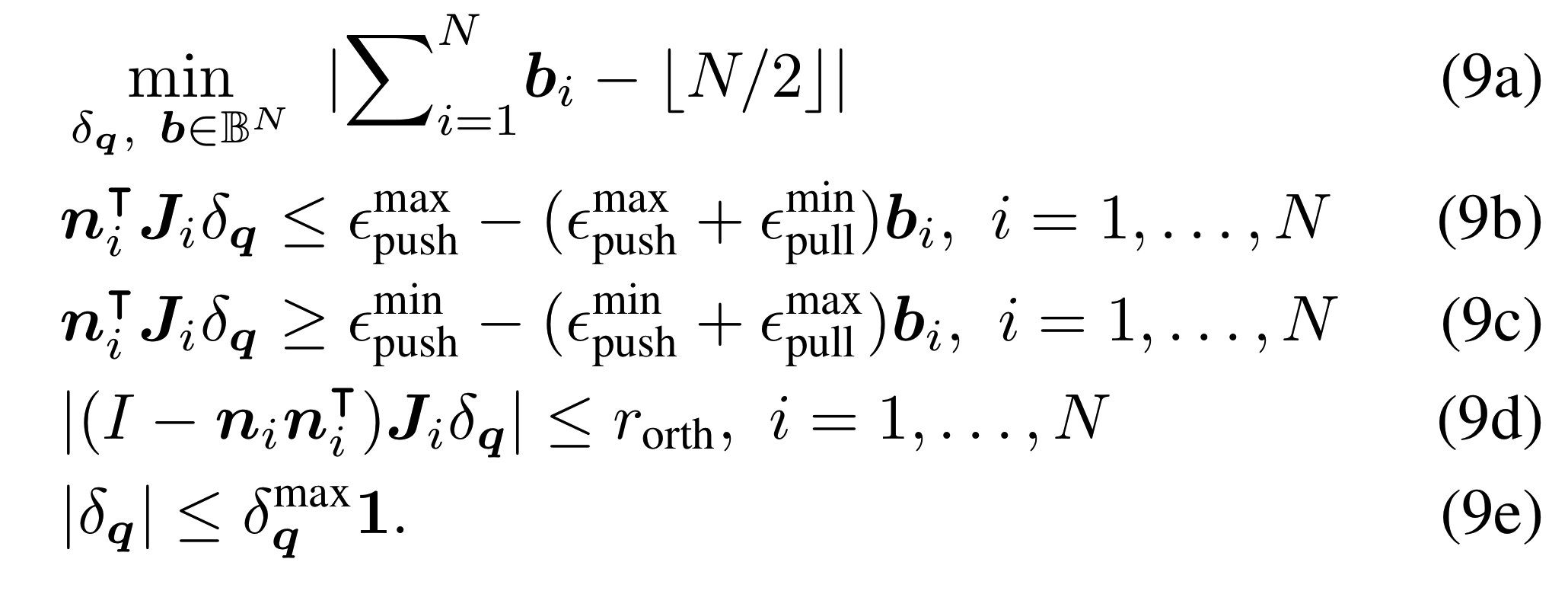
Total number of contacts.
Normal and Jacobian at contact \(i\).
Push/pull at contact \(i\).
Constrains sideways motion.
Small motion.
Take-aways
- Detecting contacts from \(\bm{\tau}_\text{ext}\) on multiple links is probably not reliable in practice.
- Needs low-noise, unbiased estimate of \(\bm{\tau}_\text{ext} \).
- Can be ambiguous even in the single contact case.
- Cannot handle more than one contacts simultaneously.
- Tactile skin is perhaps the better solution?
How well does this work?
| No. Tests | Gradient Descent successes* | Success% | RDGD successes |
Success% | |
|---|---|---|---|---|---|
| CPF succeeds | 7551 | 7326 | 97% | ||
| CPF no detection | 916 | 874 | 95% | ||
| CPF too far away | 1365 | 1112 | 81% | 1255 | 92% |
- * Success means the true contact location is within 1cm of at least 1 of the samples gradient descent converges to.
- 50 gradient descents are run on each link, with number of iterations capped at 100.
Failure modes
-
Many of the failures are due to anomalies in the mesh: "grooves (test 9701) and ledges".
-
Improve mesh quality.
-
-
Some are due to failures in proximity queries
-
Use signed distance field instead of bounding volume hierarchy?
-
Flipped normal
test id 4838
Proximity query returns a point "off-mesh".
test id 510
True contact on a "ledge", not covered by samples. Therefore the local minimum doesn't exist on the robot surface.
test id 868
Find all local minima of \(l(\cdot; \bm{q}, \bm{\tau}_\text{ext})\) with Rejection Sampling + Gradient Descent (RSGD)
- \(P_\delta\): set of accepted samples.
- \(P_\delta^*\): set of optimized samples.
- Accepted / all samples: 172/1000
- Link 5 , converged_samples / accepted samples: 78/84
- Link 6 , converged_samples / accepted samples: 80/88
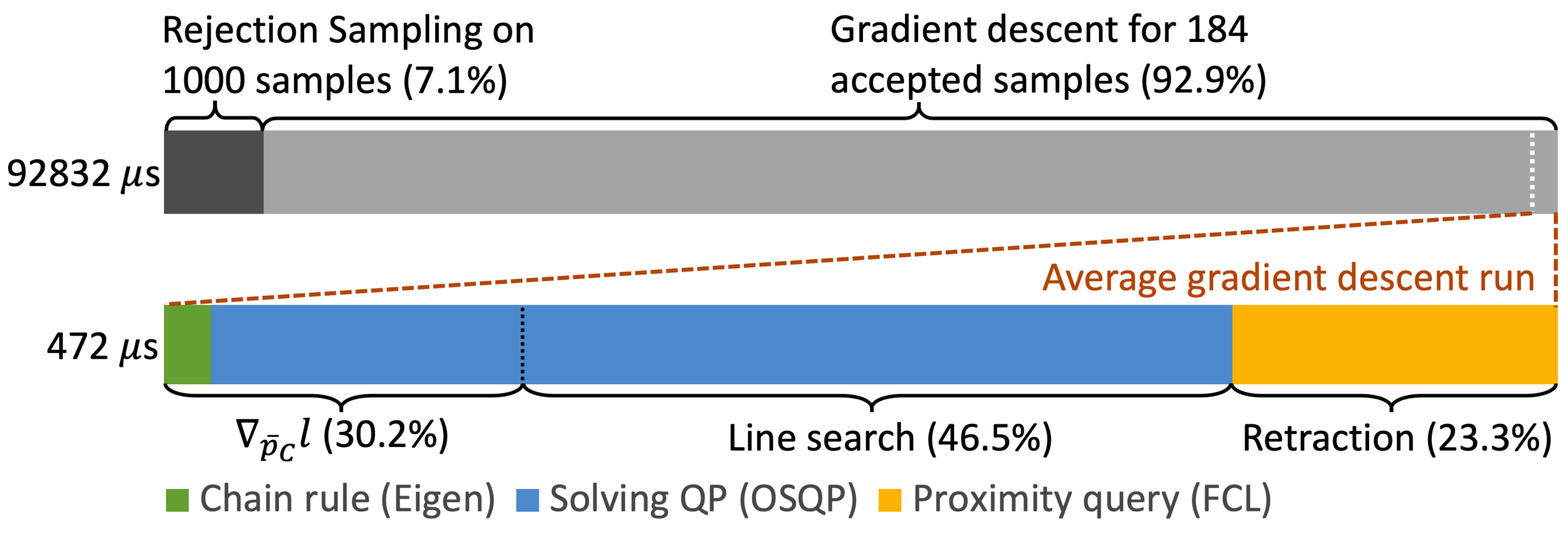
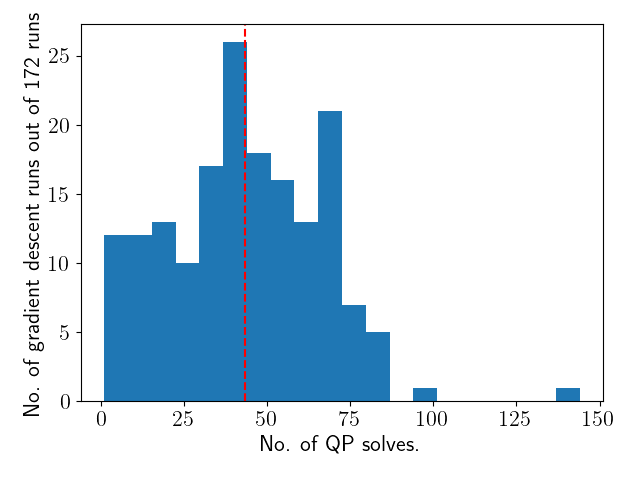
Average Number of QP solves per gradient descent: 43.4.
Contact from joint torque ICRA21
By Pang
