Contact Detection from Joint Torque Measurements
\newcommand{\rv}[1]{\mathsfit{#1}}
\newcommand{\rvv}[1]{\bm{\mathsfit{#1}}}
Pang, joint work with Jack
Recap
- We would like to solve
for the contact position \(\bm{p}_C\) and contact force \(\bm{f}_C\), subject to
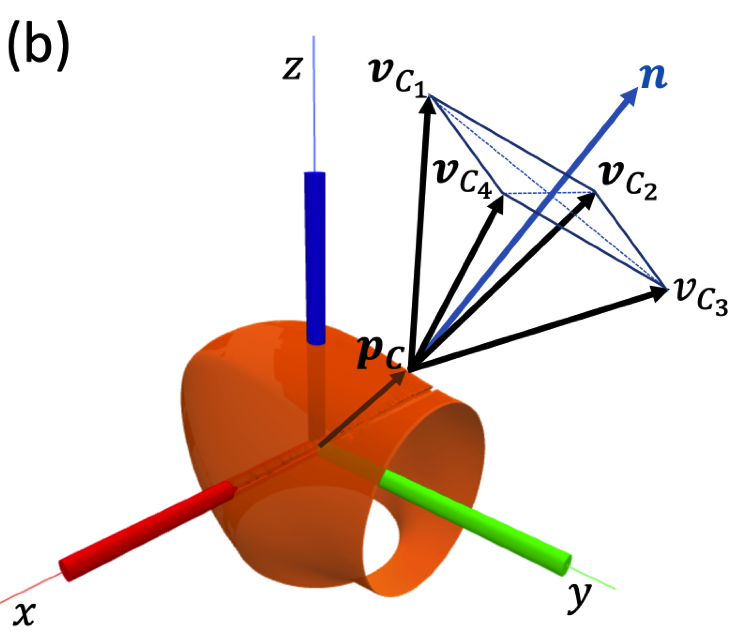
- \(\bm{p}_C \in \mathcal{S}\): point C is on the robot's surface.
-
\(\bm{f}_C \in \mathcal{K}_C\): force \(\bm{f}_C\) is inside the friction cone at C.
\bm{\tau}_\text{ext} = \bm{J}_C(\bm{q}, \bm{p}_C)^\intercal \bm{f}_C,
- This is equivalent to solving
\underset{\bm{\beta} \geq 0, \; \bar{\bm{p}}_C \in \mathcal{S}}{\text{min.}} \; \| \bm{J}(\bm{q}, \bar{\bm{p}}_C)^{\intercal} \bm{\beta} - \bm{\tau}_\text{ext} \|^2.
\newcommand{\tauE}{\bm{\tau}_{\text{ext}}}
\newcommand{\pCbar}{\bar{\bm{p}}_C}
\begin{aligned}
&l(\pCbar; \bm{q}, \tauE) \coloneqq \underset{\bm{\beta} \geq 0}{\text{min.}} \; \| \bm{J}(\bm{q}, \pCbar)^{\intercal} \bm{\beta} - \bm{\tau}_\text{ext} \|^2 \\
=& \underset{\bm{\beta} \geq 0}{\text{min.}} \left(\bm{\beta}^\intercal \underbrace{\bm{J}\bm{J}^\intercal}_{\bm{Q}} \bm{\beta} - 2 \left(\underbrace{\bm{J} \tauE}_{-\bm{b}}\right)^\intercal \bm{\beta} + \tauE^\intercal \tauE \right).
\end{aligned}
- The cost of a one contact point C is written as
- Common assumptions:
- Only one external contact.
- Contacts create no moment about the contact point.
Components of \(\bm{f}_C\) along \(\bm{v}_{C_i}\).
Link 6 of IIWA.
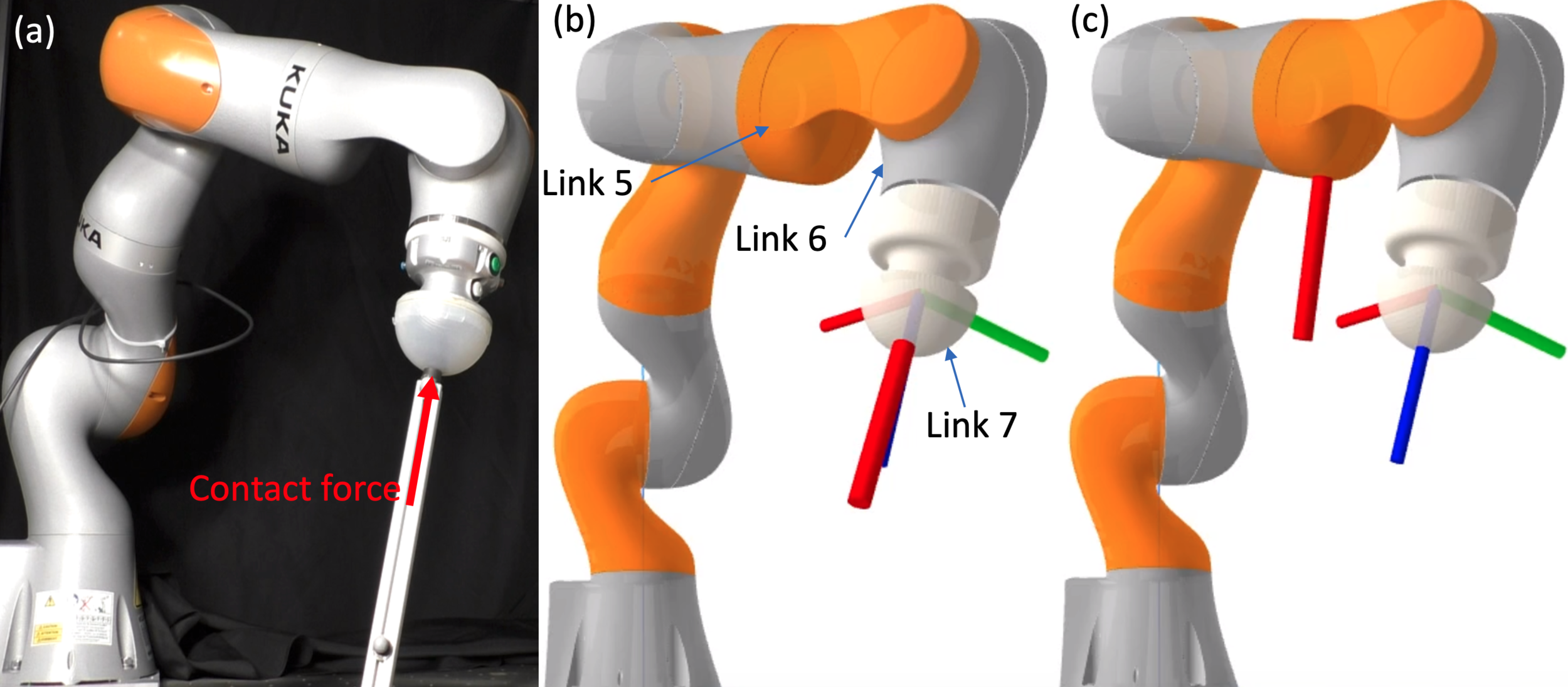
Multiple Local minima of
l(\cdot; \bm{q}, \bm{\tau}_\text{ext})
- In general, the best achievable contact estimate from joint torque measurements is not a unique point, but a set of points which are the global minima of
- We propose an algorithm to find all local minima of
- Considering that torque measurements are noisy, knowing the local minima in addition to the global ones could actually be beneficial.
l(\cdot; \bm{q}, \bm{\tau}_\text{ext})
l(\cdot; \bm{q}, \bm{\tau}_\text{ext})
Find local minima of \(l(\cdot; \bm{q}, \bm{\tau}_\text{ext})\) with Rejection Sampling + Gradient Descent
- Rejection sampling: sample points on the robot's surface, take the points with \(l \leq \epsilon\).
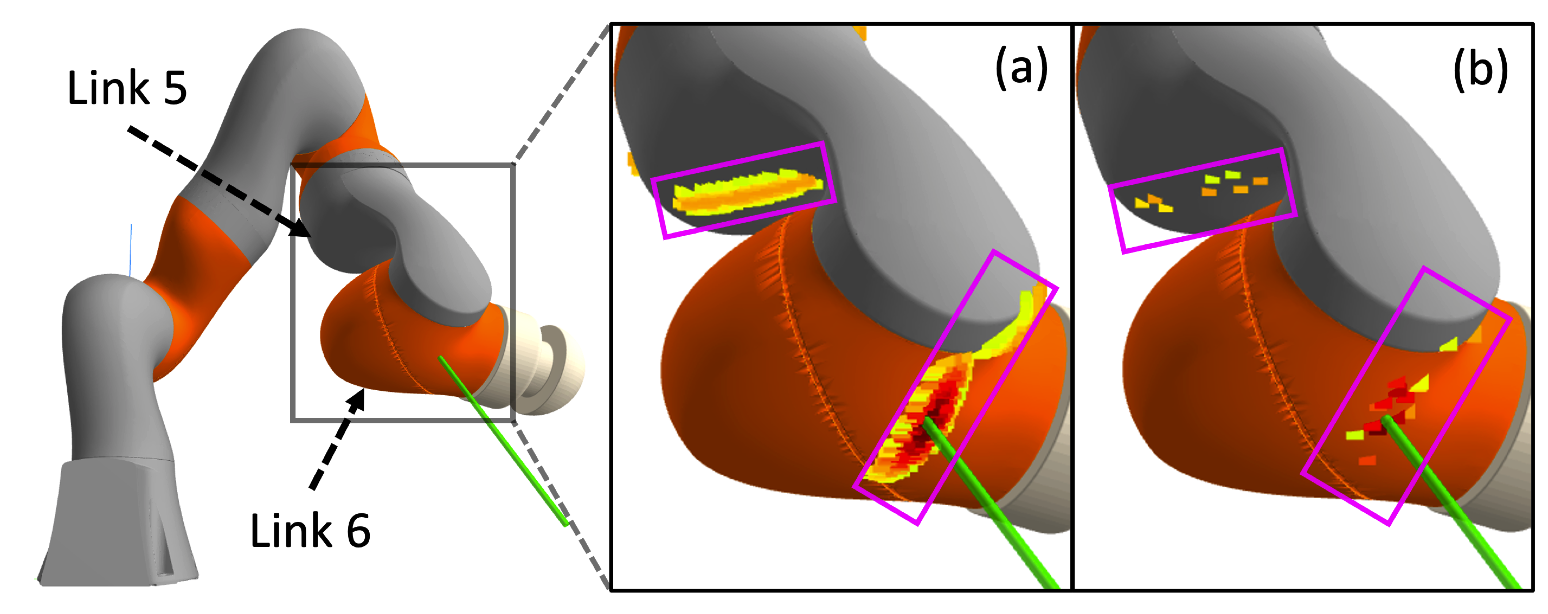
(a): accepted samples out of 10000 samples/link.
(b): accepted samples out of 500 samples/link.
Rejection rate is 98% with \(l < 0.005\).
Find local minima of \(l(\cdot; \bm{q}, \bm{\tau}_\text{ext})\) with Rejection Sampling + Gradient Descent
- Rejection sampling with a larger threshold \(\delta\).
- Run gradient descent on the accepted samples to converge to local minima of \(l(\cdot)\).
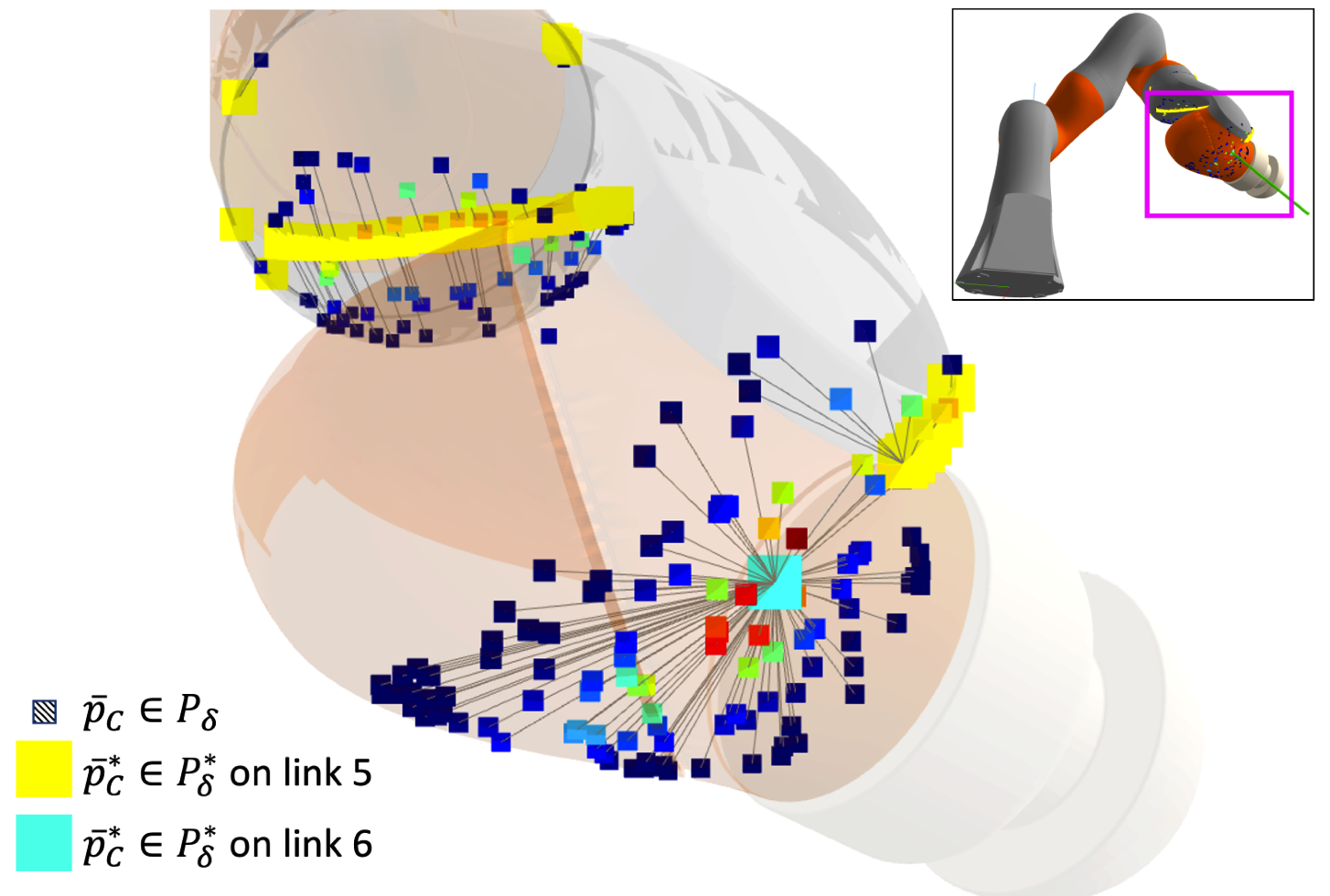
- \(P_\delta\): set of accepted samples.
- \(P_\delta^*\): set of optimized samples.
- Acceptance rate rises to 17.5% with \(\delta = 0.1\)
Find local minima of \(l(\cdot; \bm{q}, \bm{\tau}_\text{ext})\) with Rejection Sampling + Gradient Descent
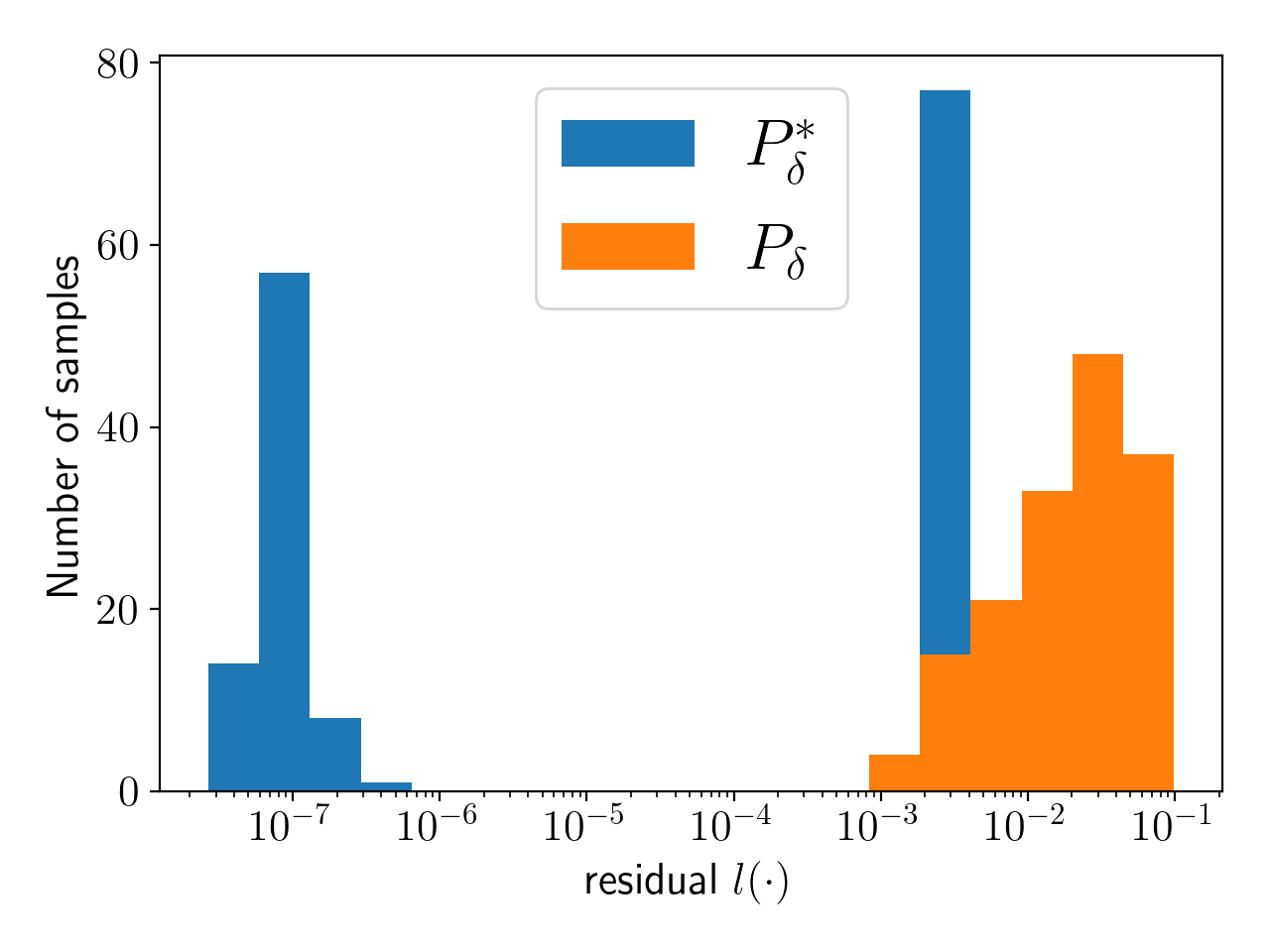
- \(P_\delta\): set of accepted samples.
- \(P_\delta^*\): set of optimized samples.
- Accepted / all samples: 172/1000
- Link 5 , converged_samples / accepted samples: 78/84
- Link 6 , converged_samples / accepted samples: 80/88
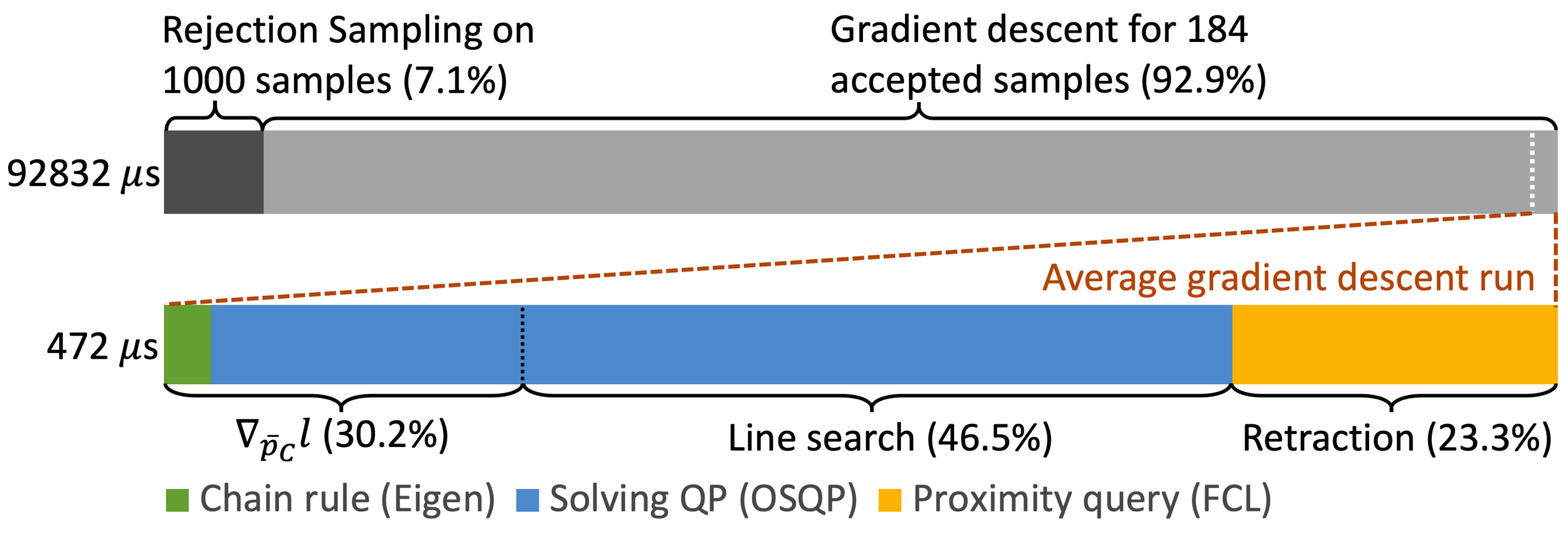
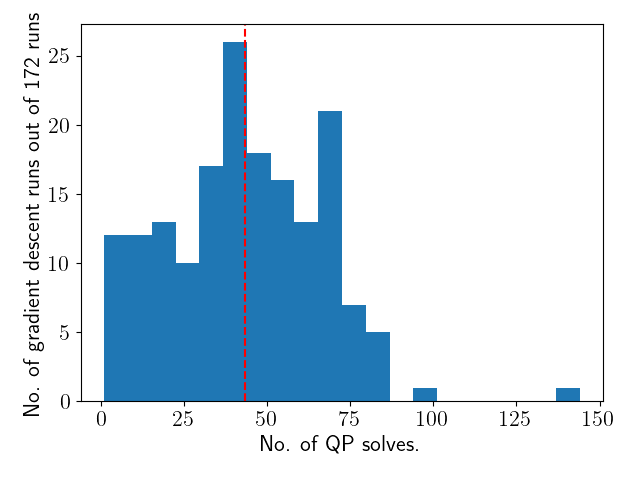
Average Number of QP solves per gradient descent: 43.4.
Works in other cases too!
Active Contact Discrimination
- Disambiguate candidate contact positions found by Rejection Sampling + Gradient Descent by making small motions.
Active Contact Discrimination
- Disambiguate candidate contact positions found by Rejection Sampling + Gradient Descent.
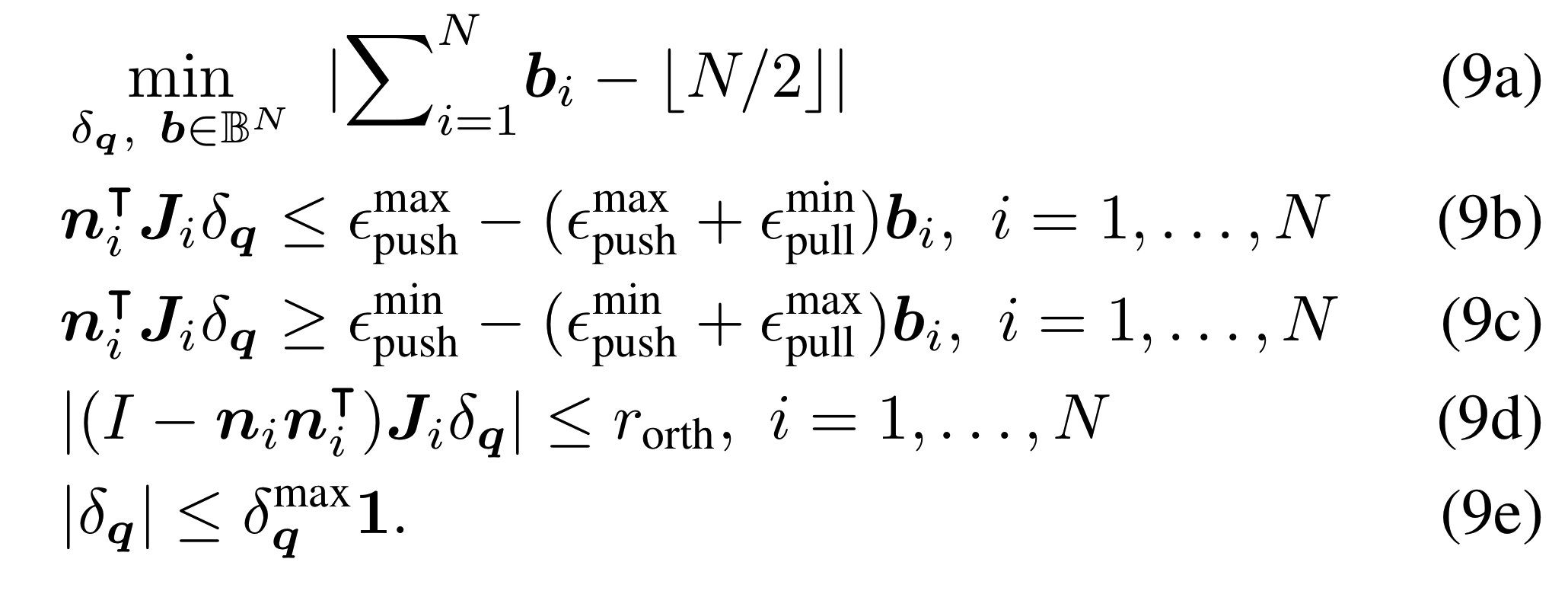
Total number of contacts.
Normal and Jacobian at contact \(i\).
Push/pull at contact \(i\).
Constrains sideways motion.
Small motion.
Take-away
- Detecting contacts from \(\bm{\tau}_\text{ext}\) on multiple links is probably not reliable in practice.
- Tactile skin is perhaps the better solution?
Contact detection from joint torque group meeting short talk
By Pang
