Reconstructing 3D geometry from Neural Radiance Field (NeRF)
Tao Pang

- Hold right mouse button: pan.
- Mouse wheel: zoom.
What is NeRF?
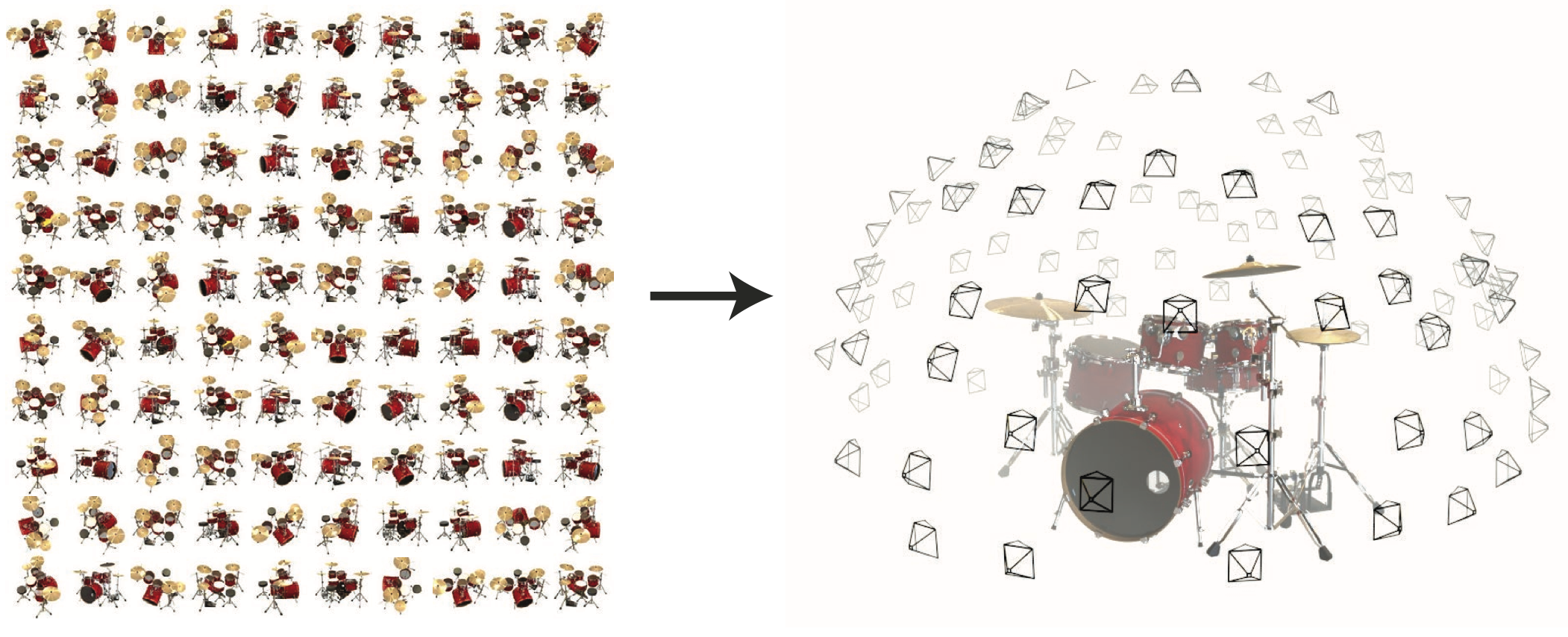
Training data: posed images
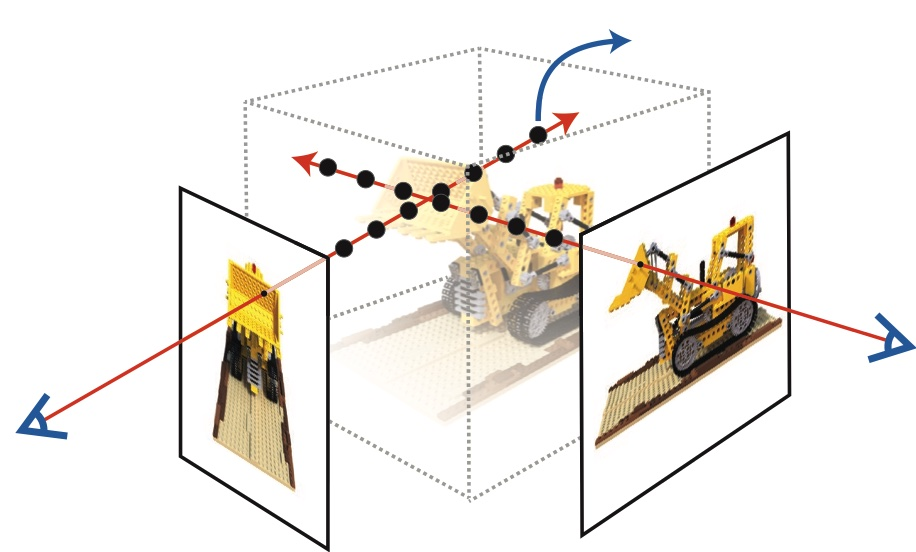
\((x, y, z)\): point in the 3D volume containing the scene.
\(d\): direction at which the camera looks at the point.
(x_i, y_i, z_i)
d
\sigma = f_{\sigma, \theta}(x, y, z)

Goal: render new views.
Intensity:
Learns
Color(RGB):
C(x, y, z, d) = f_{RGB, \theta}(x, y, z, d)
Volumetric rendering
The color of a pixel is the weighted sum of the colors along the ray.
C_{\text{pixel}} = \sum_i w_i C(x_i, y_i, z_i, d)
The weight \(w_i\) of a point is high if:
- it has high intensity \(\sigma_i\) (\(\alpha = 1\)), and
- it is not blocked by another high intensity point.
Depth can also be estimated from NeRF:
NeRF:
z_{\text{pixel}} = \sum_i w_i z_i
(similar to \(\alpha\))
w_0 = 1
w_1 = 0
(x_0, y_0, z_0)
(x_1, y_1, z_1)
camera ray
Pixel (a)
z = z_0
camera ray
Pixel (b)
w_0 = 0.5
w_1 = 0.5
(x_0, y_0, z_0)
(x_1, y_1, z_1)
z = (z_0 + z_1) / 2
Color depends on direction.
- To capture effects such as specular reflection, the direction \(d\) in \(C(x, y, z, d)\) is essential.



Pre-trained
\(C(x, y, z)\)
\(C(x, y, z, d)\)
Accurate geometry depends on direction too!
Pre-trained
- It turns out that making color a function of direction \(d\) also improves the quality of learned scene geometry.
- Geometry can be reconstructed from RGBD images synthesized for different views. (The authors' website took a different approach)
\(C(x, y, z)\)
\(C(x, y, z, d)\)
Position-only formulation learns color variation by adding extraneous geometry!




Brighter
darker
Pixel (a)
Pixel (b)
Mesh from TSDF volume
Pre-trained
\(C(x, y, z)\)
\(C(x, y, z, d)\)
Mesh from Marching cubes
- Bullet One
- Bullet Two
- Bullet Three
Pre-trained
Position only
Position and direction
Backup slides
Pixel a
Pixel b
Title Text








Title Text








Title Text
- Bullet One
- Bullet Two
- Bullet Three









nerf_6_869_spring2021
By Pang
nerf_6_869_spring2021
- 811



