An introduction to automatic differentiation

[Baydin et al., 2015, Automatic differentiation in machine learning: a survey]

https://arxiv.org/abs/1502.05767

Automatic differentiation ?

- Method to compute the differential of a function using  a computer 

Input

def f(x):
  return x ** 2


f(1.)
>>>> 1.

Output

g = grad(f)


g(1.)
>>>> 2.0

Automatic differentiation ?

- Method to compute the differential of a function using  a computer 

Input

def f(x):
  return np.log(1 + x ** 2) / x


f(1.)
>>>> 0.6931471805599453

Output

g = grad(f)


g(1.)
>>>> 0.3068528194400547

Prototypical case 

\(f\) defined recursively:

  • \(f_0(x) = x\)
  • \(f_{k+1}(x)  = 4 f_{k}(x) (1 - f_k(x))\)

Input

def f(x, n=4):
  v = x
  for i in range(n):
    v = 4 * v * (1 - v)
  return v


f(0.25)
>>>> 0.75

Output

g = grad(f)


g(0.25)
>>>> -16.0

Automatic differentiation is not...

Numerical differentiation 

$$f'(x) \simeq \frac{f(x + h) - f(x)}{h}$$

In higher dimension:

$$ \frac{\partial f} {\partial x_i} (\mathbf{x}) \simeq \frac{f(\mathbf{x} + h \mathbf{e}_i) - f(\mathbf{x})}{h}$$

Drawbacks:

  • Computing \(\nabla f = [\frac{\partial f}{\partial x_1}, \cdots, \frac{\partial f}{\partial x_n}]\) takes \(n\) computations 
  • Inexact method
  • How to choose \(h\)?

Automatic differentiation is not...

Numerical differentiation 

Example:  

from scipy.optimize import approx_fprime


approx_fprime(0.25, f, 1e-7)
>>>> -16.00001599

Automatic differentiation is not...

Symbolic differentiation

- Takes as input a function specified as symbolic operations

- Apply the usual rules of differentiation to give the derivative as symbolic operations

 

Example:

\(f_4(x) = 64x(1−x)(1−2x)^2 (1−8x+ 8x^2 )^2\), so:

f'_4(x) = 128x(1 − x)(−8 + 16x)(1 − 2x)^2(1 − 8x+ 8x^2)+ 64(1−x)(1−2x)^2(1−8x+ 8x^2)^2−64x(1 − 2x)^2(1 − 8x+ 8x^2)^2 − 256x(1 − x)(1 −2x)(1 − 8x + 8x^2 )^2

Then, evaluate \(f'(x)\)

Automatic differentiation is not...

Symbolic differentiation

- Exact

- Expression swell: derivatives can have many more terms than the base function

 

        \(f_n\)                                     \(f'_n\)                                          \(f'_n\)  (simplified)

Automatic differentiation:

Apply symbolic differentiation at the elementary operation level and keep intermediate numerical results, in lockstep with the evaluation of the main function.

 

- Function = graph of elementary operations

- Follow the graph and differentiate each operation using differentiation rules (linearity, chain rule, ...)

def f(x, n=4):
  v = x
  for i in range(n):
    v = 4 * v * (1 - v)
  return v


f(0.25)
>>>> 0.75
def g(x, n=4):
  v, dv = x, 1.
  for i in range(n):
    v, dv = 4 * v * (1 - v), 4 * dv * (1 - v) - 4 * v * dv
  return dv


g(0.25)
>>>> -16.0

Forward automatic differentiation:

Apply symbolic differentiation at the elementary operation level and keep intermediate numerical results, in lockstep with the evaluation of the main function.

 

- Function = graph of elementary operations

- Follow the graph and differentiate each operation using differentiation rules (linearity, chain rule, ...)

 

- If \(f:\mathbb{R}\to \mathbb{R}^m\): need one pass to compute all derivatives :)

- If \(f:\mathbb{R}^n \to \mathbb{R}\): need \(n\) passes to compute all derivatives :( 

- Bad for ML

Reverse automatic differentiation: Backprop

- Function = graph of elementary operations

- Compute the graph and its elements

- Go through the graph backwards to compute the derivatives

def f(x, n=4):
  v = x
  for i in range(n):
    v = 4 * v * (1 - v)
  return v


f(0.25)
>>>> 0.75
def g(x, n=4):
  v = x
  memory = []
  for i in range(n):
    memory.append(v)
    v = 4 * v * (1 - v)
  dv = 1
  for v in memory[::-1]:
    dv = 4 * dv * (1 - v) - 4 * dv * v
  return dv


g(0.25)
>>>> -16.0

Reverse automatic differentiation: Backprop

- Function = graph of elementary operations

- Compute the graph and its elements

- Go through the graph backwards to compute the derivatives

 

-Only one passe to compute gradients of functions \(\mathbb{R}^n \to \mathbb{R}\) :)

Example on a 2d function

$$f(x, y) = yx^2, \enspace x = y= 1$$

Function

 \(x =1\) 

 \(y = 1\)

 

 \(v_1 = x^2 = 1\)

 \(v_2 =yv_1 = 1\)

 

\(f = v_2 =1\)

Forward AD (w.r.t. \(x\))

 

 

 

 

 

 

 

 

Backprop \( \)

 

 

 

 

 

 

 

 

 \(\frac{dx}{dx} =1\) 

 \(\frac{dy}{dx} = 0\)

 \(\frac{dv_1}{dx} =2x \frac{dx}{dx} = 2\)

 \(\frac{dv_2}{dx} =y\frac{dv_1}{dx} +v_1 \frac{dy}{dx} =2\)

\(\frac{df}{dx} = \frac{dv_2}{dx}=2\)

 \(\frac{df}{dv_2}= 1\)

 \(\frac{df}{dy} = \frac{df}{dv_2 }\frac{dv_2}{dy} = \frac{df}{dv_2 }v_1 = 1\)

 \(\frac{df}{dv_1} =y\frac{df}{ dv_2} = 1\)

 \(\frac{df}{dx} = 2 x \frac{df}{dv_1} = 2\)

Automatic differentiation:

- Exact

- Takes about the same time to compute the gradient and the function

- Requires memory: need to store intermediate variables 

- Easy to use

- Available in Pytorch, Tensorflow, jax, package autograd with numpy

from autograd import grad

g = grad(f)


g(0.25)
>>>> -16.0

Automatic differentiation  applications

Example 0: Differentiating a sequence of transforms

Let \(g_0, \dots, g_{N-1}\) a sequence of functions, and consider the transform staring from \(x\):

 

- \(x_0 = x\)

- \(x_{n + 1} = g_n(x_n)\) for n=0...N-1

 

Consider a final cost function \(G(x) = \ell(x_N)\) where \(\ell\) is differentiable.
 

What is the gradient of G?

Example 0: Differentiating a sequence of transforms

We can apply forward differentiation (classical chain rule):

 

\(x_{n+1} = g_n(x_n)\) so \(\frac{\partial x_{n+1}}{\partial x} = J_n \times \frac{\partial x_n}{\partial x}\).  

 

Iterating this relationship:

 

\(\frac{\partial x_{N}}{\partial x}  =J_{N-1}\times \dots\times J_0 \)

 

and finally \(\nabla G(x) = \nabla \ell(x_N)J_{N-1}\times \dots\times J_0 \)

\(J_n\) is the Jacobian of \(g_n\) at \(x_n\)

Example 0: Differentiating a sequence of transforms

 

- \(x_0 = x\)

- \(x_{n+1} = g_n(x_n)\)

- \(G(x) = \ell(x_N)\)

 

We have found \(\nabla G(x) = \nabla \ell(x_N)J_{N-1}\times \dots\times J_0 \)

Will backprop give us another formula? 

What is the difference? 

Example 1: Computing Stochastic gradients in Neural networks

Neural network with parameters \(\theta\): function \(f_{\theta}(x)\)

E.g. defined recursively:

 

- \(x_0 = x\)

- \(x_{k + 1} = \sigma(W_kx_k + b_k)\)

- \(f_{\theta}(x) = x_K\)

 

Here, \(\theta = (W_0, b_0, \dots, W_{K - 1}, b_{K-1})\). 

 

Note! Can have much more complicated architecture

Example 1: Computing Stochastic gradients in Neural networks

- \(x_0 = x\)

- \(x_{k + 1} = \sigma(W_kx_k + b_k)\)

- \(f_{\theta}(x) = x_K\)

 

Supervised learning: we want \(f_{\theta}(x) \simeq y\)

We have a Training set: \((x^1, y^1), \dots, (x^n, y^n)\)

Training program: find \(\theta\) that minimizes

 

$$C(\theta) =  \frac1n\sum_{i=1}^n \ell(f_{\theta}(x^i), y^i)$$

Example 1: Computing Stochastic gradients in Neural networks

- \(x_0 = x\)

- \(x_{k + 1} = \sigma(W_kx_k + b_k)\)

- \(f_{\theta}(x) = x_K\)

 

Minimize

$$C(\theta) =  \frac1n\sum_{i=1}^n \ell(f_{\theta}(x^i), y^i)$$

How can we compute \(\nabla C(\theta)\)?

Autodiff ! \(C(\theta)\) is obtained by a sequence of elementary operations.

Example 1: Computing Stochastic gradients in Neural networks

- \(x_0 = x\)

- \(x_{k + 1} = \sigma(W_kx_k + b_k)\)

- \(f_{\theta}(x) = x_K\)

 

Autodiff is used everywhere in modern machine learning.

 

Memory issues! To apply bacward autodiff, need to store all intermediate activations \(x_k\): sometimes very costly.

Much more expensive to train than to simply evaluate a neural network

Example 2: Learning to learn

Ridge regression: minimize \(\ell(\beta) = \frac12 \| X \beta - y\|^2 + \frac\lambda 2\|\beta\|^2\)

 

Gradient descent with step \(\rho > 0\) for \(T\) iterations: 

- \(\beta_0 = 0\)

- \(\beta_{t+1} = \beta_t - \rho( X^{\top}(X\beta -y) + \lambda \beta)\)  

 

We see it as a function \(GD:\rho \to \beta_T\).

 

What is the best \(\rho\) ?

[Gregor, Lecun, 2010, Learning Fast Approximations of Sparse Coding]

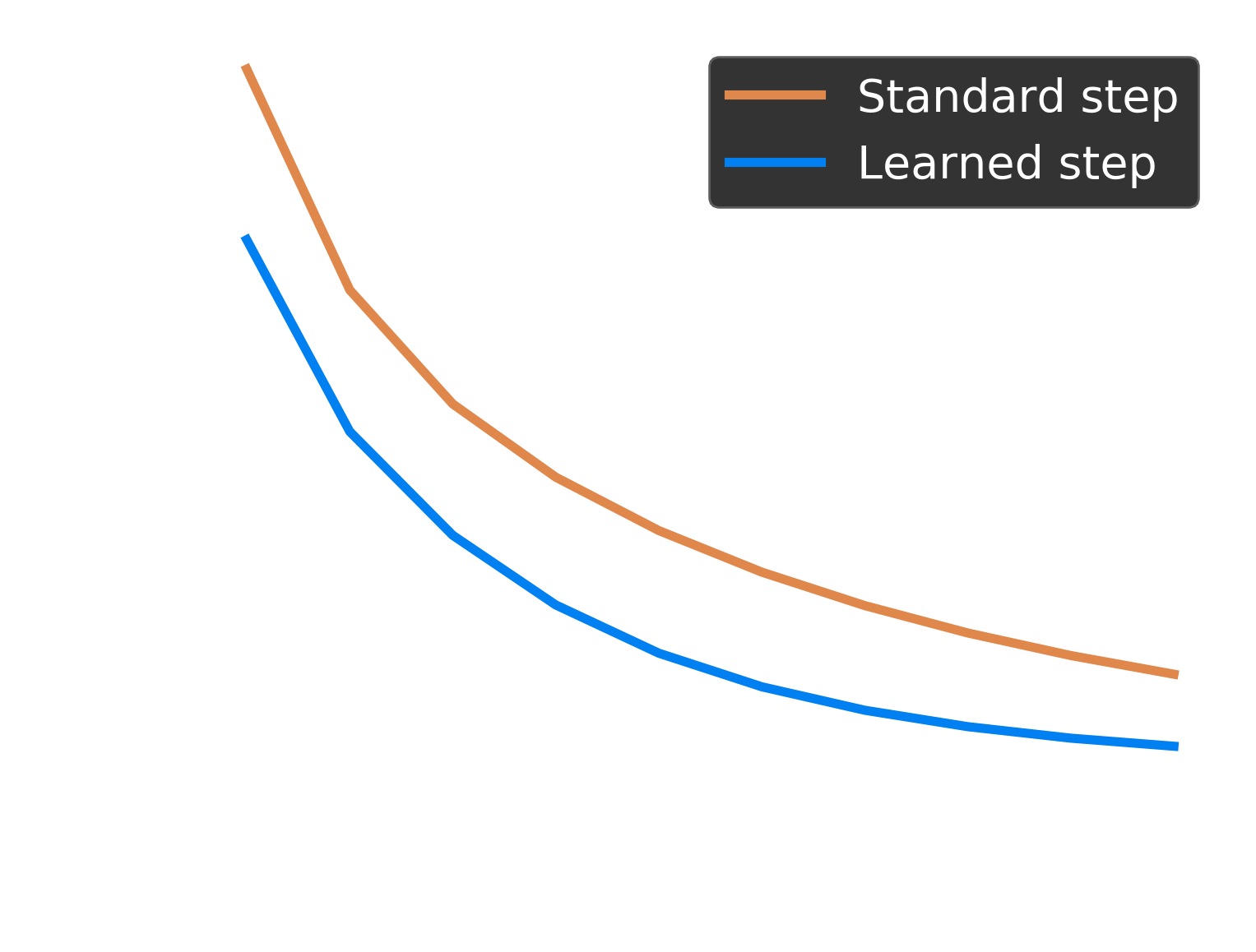
Example 2: Learning to learn

Ridge regression: minimize \(\ell(\beta) = \frac12 \| X \beta - y\|^2 + \frac\lambda 2\|\beta\|^2\)

We want to find \(\rho\) that minimizes \(\ell(GD(\rho))\)

 

\(\to\) use gradient descent! 

 

$$ \rho \leftarrow \rho - 0.01 \nabla_{\rho}\ell(GD(\rho))$$

\(\nabla_{\rho}\ell(GD(\rho))\) is computed using automatic differentiation

Example 3: hyperparameter optimization

Ridge regression: minimize \(\ell(\beta, \lambda) = \frac12 \| X \beta - y\|^2 + \frac\lambda 2\|\beta\|^2\)

 

- Assume we have a test set \(X_{test}, y_{test}\).  Find \(\lambda\) that minimizes test error:

 

$$\ell'(\lambda) = \frac12\|X_{test}\beta^*(\lambda) - y_{test}\|^2$$

subject to :

$$ \beta^*(\lambda) = \arg\min \ell(\beta, \lambda)$$

 

- In this simple case, closed-form solution for \(\beta\), but not in general

[Bengio, 1990, Gradient based optimization of hyperparameters]

Example 3: hyperparameter optimization

Ridge regression: minimize \(\ell(\beta, \lambda) = \frac12 \| X \beta - y\|^2 + \frac\lambda 2\|\beta\|^2\)

$$\ell'(\lambda) = \frac12\|X_{test}\beta^*(\lambda) - y_{test}\|^2$$

subject to :

$$ \beta^*(\lambda) = \arg\min \ell(\beta, \lambda)$$

 

Usual approach: grid search. Select a set of candidates \(\lambda_1, \dots, \lambda_k\) and pick the one that leads to smallest test error.

Problem: In order to cover space, \(k\) grows exponentially with the number of hyperparameters

Grid search is practically useless when more than 10 hyperparameters !

Example 3: hyperparameter optimization

Ridge regression: minimize \(\ell(\beta, \lambda) = \frac12 \| X \beta - y\|^2 + \frac\lambda 2\|\beta\|^2\)

$$\ell'(\lambda) = \frac12\|X_{test}\beta^*(\lambda) - y_{test}\|^2$$

subject to :

$$ \beta^*(\lambda) = \arg\min \ell(\beta, \lambda)$$

 

Idea: Use first order information

Example 3: hyperparameter optimization

Ridge regression: minimize \(\ell(\beta, \lambda) = \frac12 \| X \beta - y\|^2 + \frac\lambda 2\|\beta\|^2\)

 

$$ \min \ell'(\beta) = \frac12\|X_{test}\beta - y_{test}\|^2 \enspace \text{s.t.} \enspace \beta = \arg\min \ell(\beta, \lambda)$$

- Define the output of gradient descent \(GD: \lambda \to \beta\):

$$GD(\lambda) \simeq \argmin_{\beta} \ell(\beta, \lambda)$$

- Optimize \(\ell'(GD(\lambda))\) with gradient descent, using autodiff to compute the gradient

 

 

Better scaling with # of hyperparameters than grid-search

Thanks for you attention !

Intro_autodiff_psl

By Pierre Ablin

Made with Slides.com

Intro_autodiff_psl

  • 355

More from Pierre Ablin