Automatic Differentiation:
An Introduction

Robert Salomone
How did I get here?

I am not a computer scientist.
Application Areas
Derivative information is used in algorithms in...
- Machine Learning (Optimization)
- Computational Statistics (Sampling)
However...
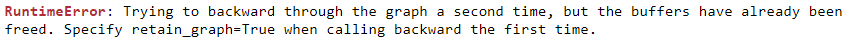
Goals
- Understand what Automatic Differentiation is and isn't.
- Understand what AD is actually doing (not taking gradients!)
- Demystify why Pytorch and Tensorflow are (seemingly) so weird.
- Demonstrate Autodiff in Python with some "advanced" features using Pytorch and Autograd.
The Good News

You can get (reasonably) far without knowing much.
The Not So Good News
You can get only get so far without knowing much.


The Plan
First Half: A gentle yet complete introduction to what AD is and what it is doing.
(key to understanding any AD software framework)
Second Half: Tour through two popular AD frameworks in Python, including some nice "tricks" to ease the learning curve.
Part I: Theory
Reference
Baydin et al. 2017. Automatic differentiation in machine learning: a survey. Journal of Machine Learning Research 18, 1.
What AD is not...
Finite Differences
For small \(h\), we have the forward difference approximation --- \(O(h)\):
and central difference approximation --- \(O(h^2)\):
Remember what a (partial) derivative is....
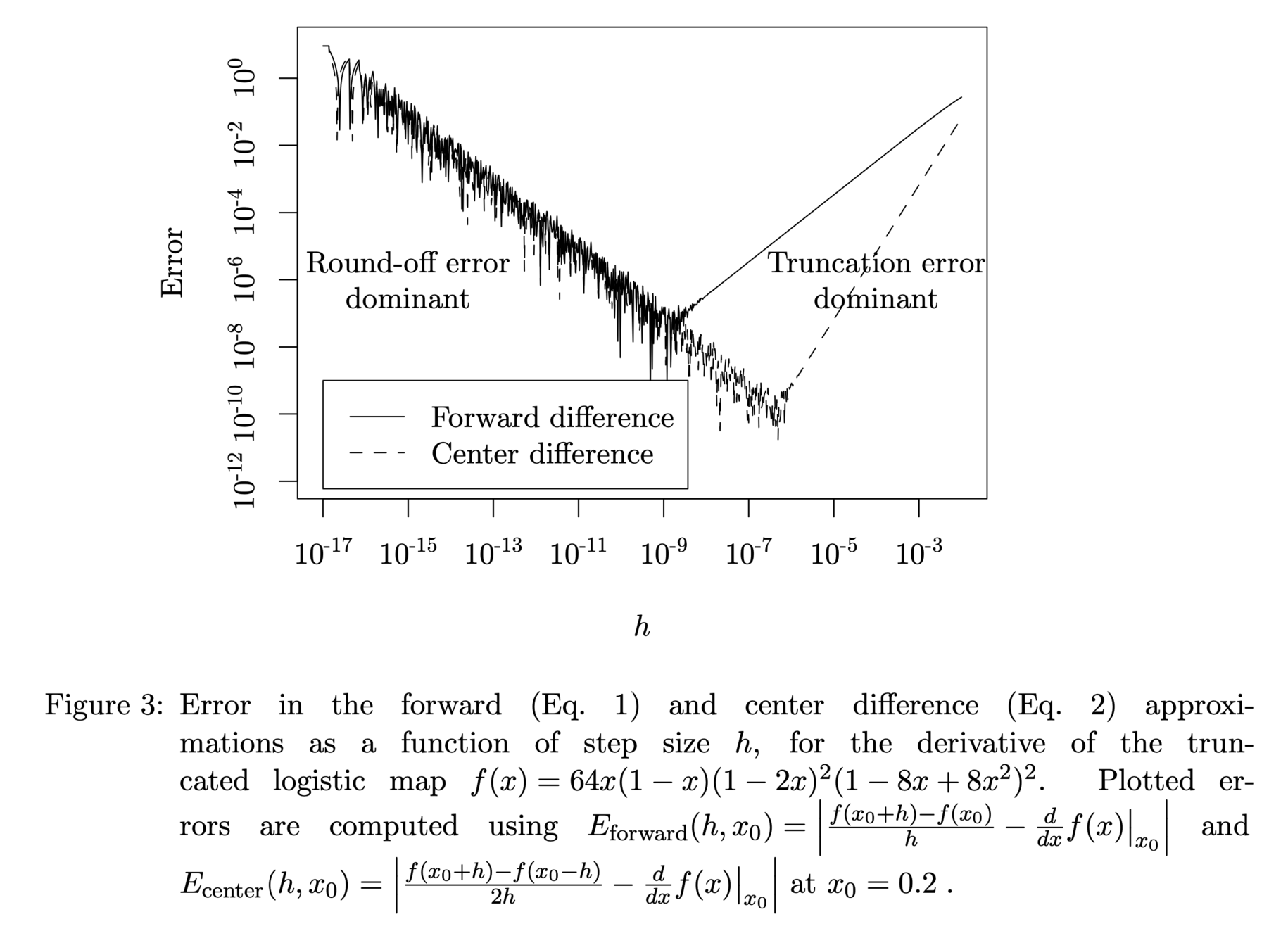
Finite differences are not only inaccurate, but also inefficient.
*from [1]
Symbolic Differentiation
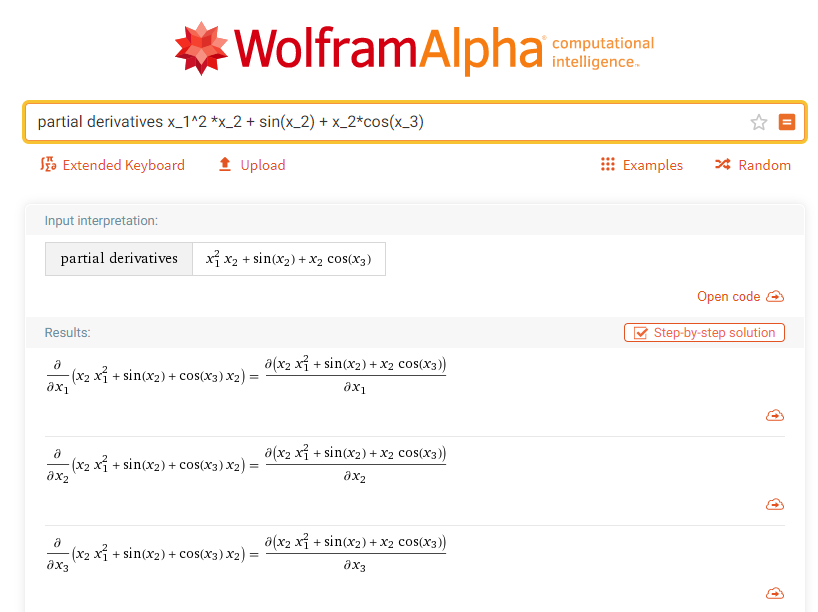
Expression Swell

* from [1]
Gradients
- Scalar-Valued Function \( f: \mathbb{R^n} \rightarrow \mathbb{R} \), i.e., \(y = f(\mathbf{x})\).
- Gradient:
Finite Difference: Approximates \(\nabla f(\mathbf{x})\), requiring (at least) \(n+1\) function evaluations for each desired \(\mathbf{x}\).
Symbolic: Computes \(\nabla f\) as its own function object. Then, requires evaluation of this object with numerical values as input.
Automatic Differentiation: Computes exactly \(\nabla f(\mathbf{x})\) and \(f(\mathbf{x})\). If done using the correct AD mode, it requires only (roughly) two function evaluations for each \(\mathbf{x}\).
Why is PyTorch / Tensorflow so confusing?
(2) Autodiff isn't really taking partial derivatives or gradients: it is doing something else.
(1) Automatic Differentiation relies on an abstract concept called a computational graph.
Solution: Understand these concepts first, then use the software.
Computation Graphs and Primal Traces
All functions are made up of more elementary functions...
\( \)
\(v_3 = v_0 v_1 \)
\(x_1\)
\(v_4 = v_2 + v_3\)
\(x_2\)
\(v_2 = 2 v_0 \)
\(v_0\)
\(v_1\)
Primal Trace
Computation Graph for \(f(x_1, x_2) = 2x_1 + x_1 x_2 \)
\(f\)
\(y\)
Exercise 1 (Graphs and Primal Trace)
Draw the computation graph and list the primal trace for the function
\(f(x_1, x_2) = \log(x_1) + x_1 x_2 - \sin(x_2)\)
Note: The graph and primal trace in general are not unique (different order / labels).
Hint: Pretend you are actually evaluating the function, and keep a running journal of what you do.

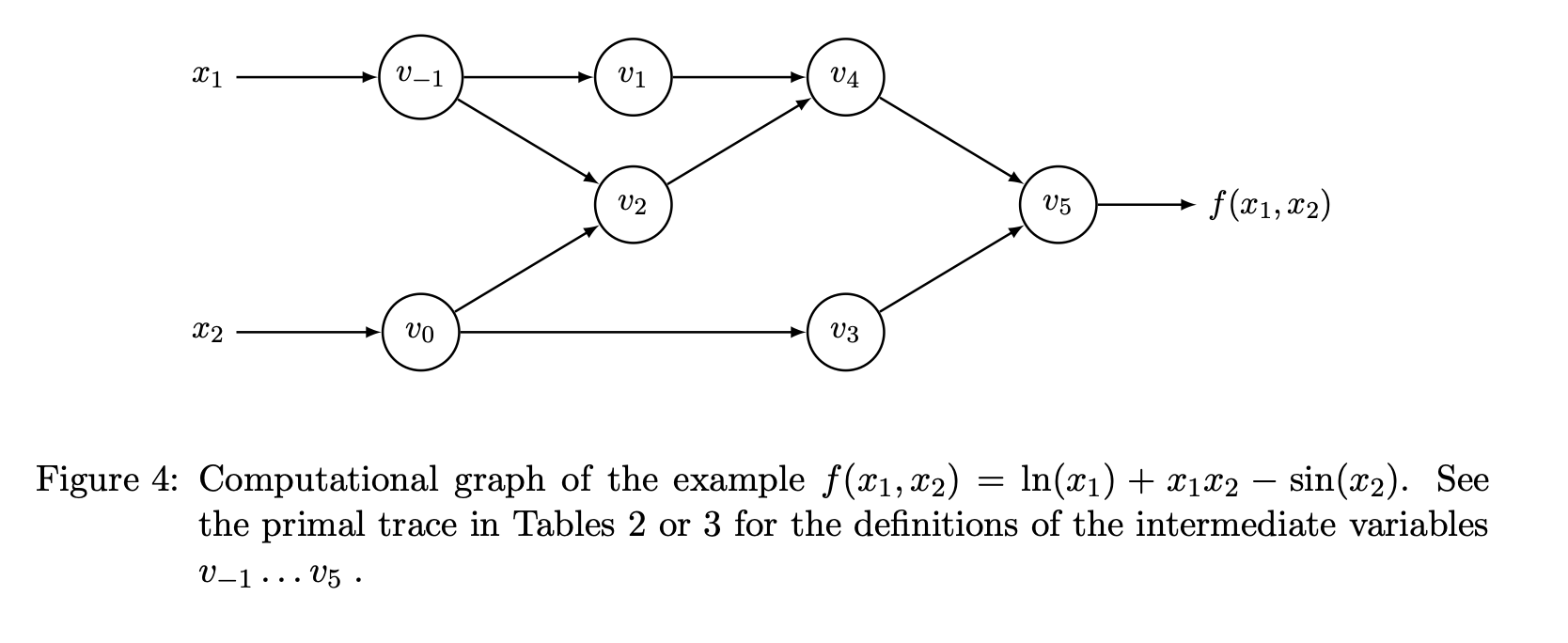
Solution (from Reference)
A graph is all you need...
- Autodiff only requires a computational graph for the input of interest.
- Can include recursions, conditionals (if statements), loops, etc.
- When you run the function, it just needs to take a trace of what it does with that input!
- This can include "fancy" stuff like...
- ODE Solver (Runge-Kutta, Implicit Euler)
- Fast Fourier Transform
- Matrix Cholesky Factorization
- Matrix (log-)Determinant
Reminder: Multivariate Chain Rule
\(z_2(x_1, x_2) = x_1 x_2 \)
\(x_1\)
\(y(z_1(x_1), z_2(x_1, x_2))\)
\(\qquad= 2x_1 + z_2(x_1, x_2)\)
\(x_2\)
\(z_1(x_1) = 2 x_1 \)
Multivariate Chain Rule
\(z_2(x_1, x_2) = x_1 x_2 \)
\(x_1\)
\(y(z_1(x_1), z_2(x_1, x_2))\)
\(\qquad= 2x_1 + z_2(x_1, x_2)\)
\(x_2\)
\(z_1(x_1) = 2 x_1 \)
Forward (Tangent) Mode AD
\(v_3 = v_0 v_1 \)
\(x_1\)
\(v_4 = v_2 + v_3\)
\(x_2\)
\(v_2 = 2 v_0 \)
\(v_0\)
\(v_1\)
\(f\)
\(y\)
Primal Trace
(Partial) Tangent Trace
$$\dot{v}_{k,i} := \frac{\partial v_k}{\partial x_{i}}$$
\(v_3 = v_0 v_1 \)
\(x_1\)
\(v_4 = v_2 + v_3\)
\(x_2\)
\(v_2 = 2 v_0 \)
\(v_0\)
\(v_1\)
\(f\)
\(y\)
(Partial) Tangent Trace: \(\dot{v}_{k,i} := \frac{\partial v_k}{\partial x_{i}}\)
\(\dot{v}_{0,1} = \frac{\partial v_0}{\partial x_1}=1\)
\(\dot{v}_{2,1} = \frac{\partial v_2}{\partial x_1}=\frac{\partial v_2}{\partial v_0}\frac{\partial v_0}{\partial x_1}= \frac{\partial v_2}{\partial v_0}\dot{v}_{0,1} \)
\(\dot{v}_{3,1} = \frac{\partial v_3}{\partial x_1}=\frac{\partial v_3}{\partial v_0}\frac{\partial v_0}{\partial x_1}= \frac{\partial v_3}{\partial v_0}\dot{v}_{0,1} \)
\(\dot{v}_{4,1} = \frac{\partial v_4}{\partial x_1}=\frac{\partial v_4}{\partial v_2}\frac{\partial v_2}{\partial x_1} + \frac{\partial v_4}{\partial v_3}\frac{\partial v_3}{\partial x_1}= \frac{\partial v_4}{\partial v_3}\dot{v}_{2,1} + \frac{\partial v_4}{\partial v_3}\dot{v}_{3,1} \)
Key Aspect: only expand the chain rule once at each stage, reusing the (forward) accumulated derivatives.
Intuition
Primal Trace
Differentiability
In practice, we only need the function to be differentiable at the points we evaluate it along the tangent trace.
So e.g., the absolute value function \(|\cdot |\)
is not problematic in practice so long as we don't input zero!
Let's generalize a little...
The above is are elements of what is called the tangent trace.
Note: Initializing \(\dot{\mathbf{x}} = (1,0)\) or \(\dot{\mathbf{x}}=(0,1) \) makes \(\dot{y}\) be the derivative with respect to \(x_1\) or \(x_2\) respectively.
Let's now consider
\(v_3 = v_0 v_1 \)
\(x_1\)
\(v_4 = v_2 + v_3\)
\(x_2\)
\(v_2 = 2 v_0 \)
\(v_0\)
\(v_1\)
\(f\)
\(y\)
\(\dot{v}_0 = \dot{x}_1\)
\(\dot{v}_1 = \dot{x}_2\)
\(\dot{v}_3 = \dot{v}_0 v_1 + v_0 \dot{v}_1\)
\(\dot{v}_2 = 2\dot{v}_0 \)
\(\dot{v}_4 = \dot{v}_2 + \dot{v}_3 \)
\(\dot{y}\)
Exercise 2 (Forward Mode)
With the function from the last example, compute the tangent trace for each graph node.
\(f(x_1, x_2) = \log(x_1) + x_1 x_2 - \sin(x_2)\)
Then, use it to evaluate \(\frac{\partial f}{\partial x_1} \) at (2,5) by setting \(\dot \mathbf{x} = (1,0) \)
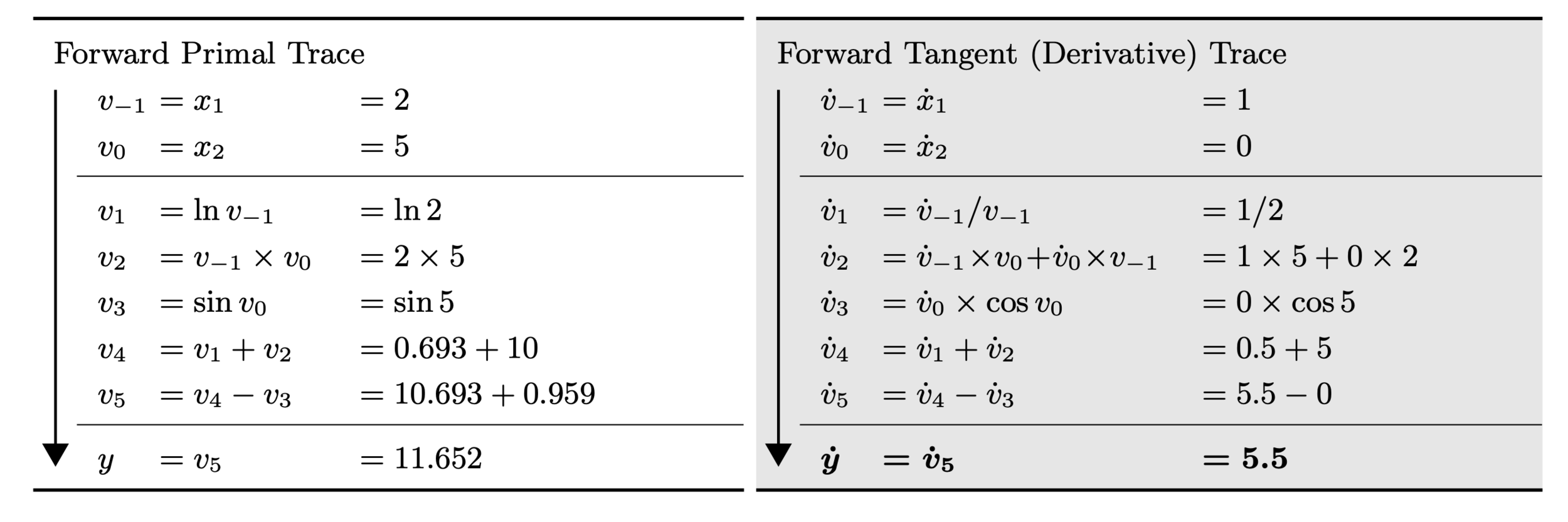
Solution
...doesn't that add redundant computation?
No, it adds magic.
(click above for answer)
Name that Mathematician

Carl Gustav Jacob Jacobi
Most famous for:
theory of elliptic functions
(also that matrix of derivatives from second-year calculus)
Jacobian Matrix
Quiz: The \(k \)-th row of \( \mathrm{J}_{\mathbf{f}}(\mathbf{x}) \) is equal to
\(\mathbf{f}: \mathbb{R}^n \rightarrow \mathbb{R}^m \)
Jacobian-Vector Product (JVP)
Forward Mode actually evaluates this for arbitrary \(\dot{\mathbf{x}}\).
The Jacobian of a scalar-valued function \(f: \mathbb{R}^n \rightarrow \mathbb{R} \) is its ...
gradient transposed: \(\nabla f(\cdot)^\top\).
In this case, the Jacobian-Vector product is equal to
i.e., the
Directional Derivative of \(f\)(\(\mathbf{x} \)) in the direction \(\mathbf{\dot{x}}\).
Look at one part...
\(v_3 = v_0 v_1 \)
\(x_1\)
\(x_2\)
\(v_2 = 2 v_0 \)
\(v_0\)
\(v_1\)
\(\dot{v}_0 = \dot{x}_1\)
\(\dot{v}_1 = \dot{x}_2\)
\(\dot{v}_3 = \dot{v}_0 v_1 + v_0 \dot{v}_1\)
\(\dot{v}_2 = 2\dot{v}_0 \)
So...
Forward accumulation computes JVPs and passes them forward...
Note that we never need to form the full Jacobian matrix/matrices!
The "Magic"
We can initialize \(\dot{\mathbf{x}} = \mathbf{r}\) and compute any JVP: \(\mathrm{J}_f(\mathbf{x}) \mathbf{r} \) in only one pass through the computation graph!
For \(f: \mathbb{R}^n \rightarrow \mathbb{R}\), initializing with \(\dot{\mathbf{x}}=\mathbf{e}_i\) gives the \(i\)-th partial derivative.
This involves roughly the same effort as computing the initial function twice!
More generally...
\(\mathbf{f}: \mathbb{R}^n \rightarrow \mathbb{R}^m \)
One forward mode sweep can evaluate a column of the Jacobian at \(\mathbf{x}\)!
Setting \(\dot{\mathbf{x}} = \mathbf{e}_i\) evaluates the \(i\)-th column.
Quiz
Forward mode requires sweeps of the graph to evaluate the full Jacobian.
For \(m=1\), \(\nabla f(\mathbf{x}) = \mathrm{J}_f (\bf x)^\top \) :(
For \(n=1, \mathrm{J}_f(\mathbf{x}) = \mathrm{J}_{f}(\mathbf{x})\times 1\) :D
n
Reverse (Adjoint) Mode AD
Back to Multivariate Chain Rule
\(z_2(x_1, x_2) = x_1 x_2 \)
\(x_1\)
\(y(z_1(x_1), z_2(x_1, x_2))\)
\(\qquad= 2x_1 + z_2(x_1, x_2)\)
\(x_2\)
\(z_1(x_1) = 2 x_1 \)
Reverse Mode is Generalized Backpropagation
\(\widehat{y}\)
\(y\)
\(b_1\)
\(b_2\)
\(x_1\)
\(x_2\)
\(x_3\)
Neural Net Loss Function: Backpropagation
Everything Else:
Reverse Mode AD
(Partial) Adjoints
compare with (Partial) Tangents:
(tangents go) Forward Accumulation
(adjoints go) Backward Accumulation
Exercise 3 (Reverse Mode)
With the function from the last exercises, compute the adjoint trace for each graph node.
\(f(x_1, x_2) = \log(x_1) + x_1 x_2 - \sin(x_2)\)
Solution

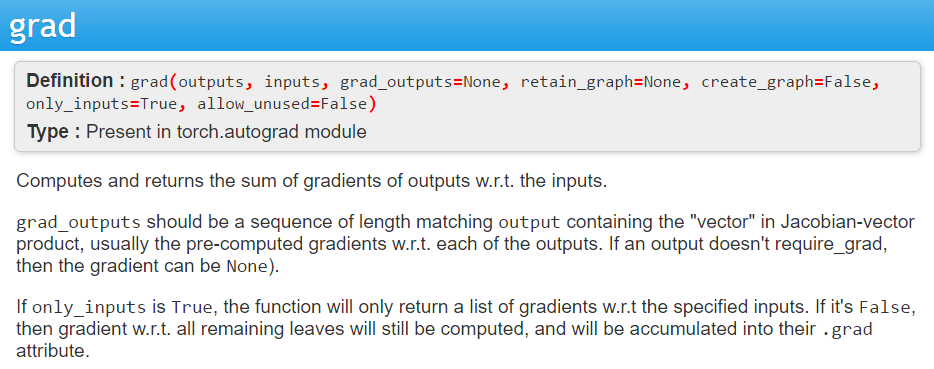
Vector Jacobian Product (VJP)
Evaluate the VJP by initializing the reverse phase with $$ \overline{\mathbf{y}} = \mathbf{r}.$$
Key Observation
This single node "backpropagation" is a Vector-Jacobian product!
\(v_3 = v_0 v_1 \)
\(x_1\)
\(x_2\)
\(v_2 = 2 v_0 \)
\(v_0\)
\(v_1\)
\(\overline{v}_0\)
\(\overline{v}_1 = \overline{x}_2\)
\(\overline{v}_3 \)
\(\overline{v}_2 \)
\(v_3 = {\rm SOLVE}_{\mathbf{y}} (\mathrm{v_0}\mathbf{y}=v_1)\)
\(\mathrm{A}\)
\(v_4 = v_2 v_3\)
\(\mathbf{x}\)
\(v_2 = \mathrm{A}^{1/2}\)
\(v_0\)
\(v_1\)
Graph nodes need not contain elementary operations: you can compress it so long as you know a nodes VJP function!
\(f\)
\(\mathbf{y}\)
Primatives
Recall that Forward Mode with unit vectors for \(\dot{\mathbf{x}}\) evaluates a column of the Jacobian.
Backward Mode with unit vectors for \(\dot{\mathbf{x}}\) evaluates a row of the Jacobian.
So what's it do?
Quiz (Reverse Mode)
For \(f: \mathbb{R}^n \rightarrow \mathbb{R}\), we can evaluate the gradient with backward sweep(s).
1
For \(f: \mathbb{R} \rightarrow \mathbb{R}^m\), we can obtain the Jacobian with backward sweep(s).
m
\(\nabla(\mathbf{x})^\top = 1 \times {\rm J_f}(\mathbf{x}) \)
(one row each time)
Automatic Differentiation: Summary
| AD Mode | Operation | |
|---|---|---|
| Forward | JVP: |
Column |
| Backward | VJP: | Row |
Can you combine the two in smart ways?
Yes
(I'll give you the most useful example...)
Hessians
- Suppose that \( f: \mathbb{R}^n \rightarrow \mathbb{R} \). Then, the Hessian of \(f \) is
$${\rm H}_{f}(\mathbf{x}) = \mathrm{J_{\nabla f}}(\mathbf{x}) = \textcolor{red}{\nabla} \big( \nabla f(\mathbf{x})\big)$$
- The Hessian is the of the of \(f\)
gradient
Jacobian
- VJP (Forward Mode) to obtain trace of (*) \(\mathbf{u}^\top\nabla f(\mathbf{x}) \)
- Take Gradient of (*) (Reverse Mode):
Hessian Vector Product (HVP)
Requires effort of (roughly) only four function evaluations!
Inverse-Hessian Vector Product
Can even evaluate \(\mathrm{H}^{-1}\mathbf{r}\) by touching only HVPs (using the Conjugate Gradient method).
e.g., Neural Net with with \(10^6\) parameters. Hessian has \(10^{12}\) elements: 8 terabytes!
Question and Discussion Time!
Part II : Practice



With its updated version of Autograd, JAX can automatically differentiate native Python and NumPy functions.
Graphics Processing Units (GPUs)

Good at doing many linear algebra operations (VJP/JVP) at once.
\(v_3 = {\rm SOLVE}_{\mathbf{y}} (\mathrm{v_0}\mathbf{y}=v_1)\)
\(\mathrm{A}\)
\(v_4 = v_2 v_3\)
\(\mathbf{x}\)
\(v_2 = \mathrm{A}^{1/2}\)
\(v_0\)
\(v_1\)
\(f\)
\(\mathbf{y}\)
\(\overline{v}_1\):JVP-2
\( \overline{v}_0\):JVP-1
Parallelization
| Forward Mode | Reverse Mode | GPU | |
|---|---|---|---|
| Tensorflow |
|||
|
PyTorch |
|||
|
Autograd |
|||
| Jax (Autograd 2.0) |
Python Frameworks
Generally reverse mode will be enough, but beware!
Where's the VJP?!
Using software that doesn't have forward mode?
You can get a JVP using a VJP of a VJP.
See Jupyter Notebook for the rest!
Automatic Differentiation
By Rob Salomone
Automatic Differentiation
- 1,019


