Modeling a traffic light warning system for acute respiratory infections as an optimal control problem
ASU-MathBio seminar
Saul Diaz Infante Velasco
Adrian Acuña Zegarra
Jorge Velasco Hernandez
sauldiazinfante@gmail.com
Guidelines for estimating the risk of the epidemiological traffic light
Vaccination camping
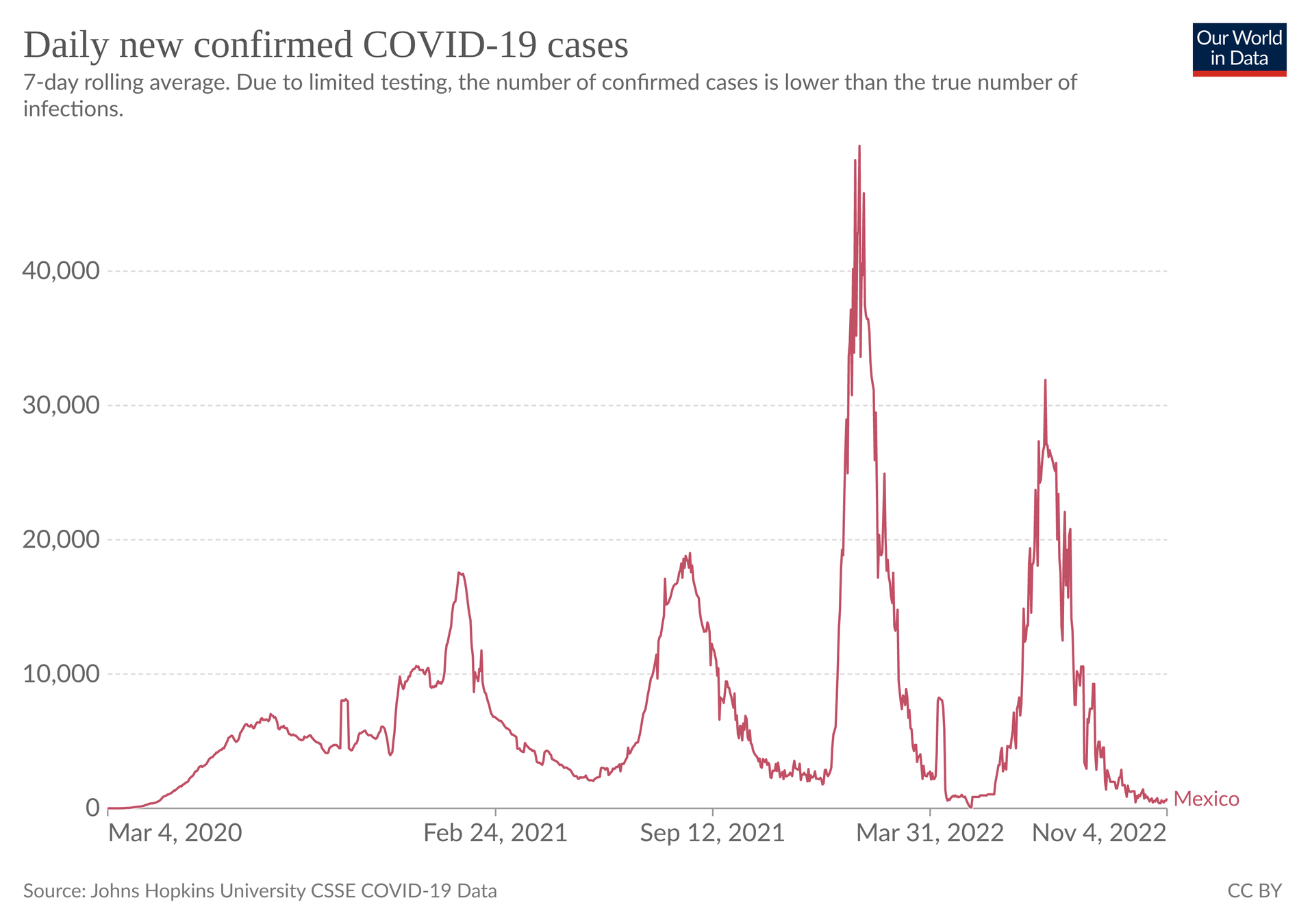
Omicron variant
Introduction
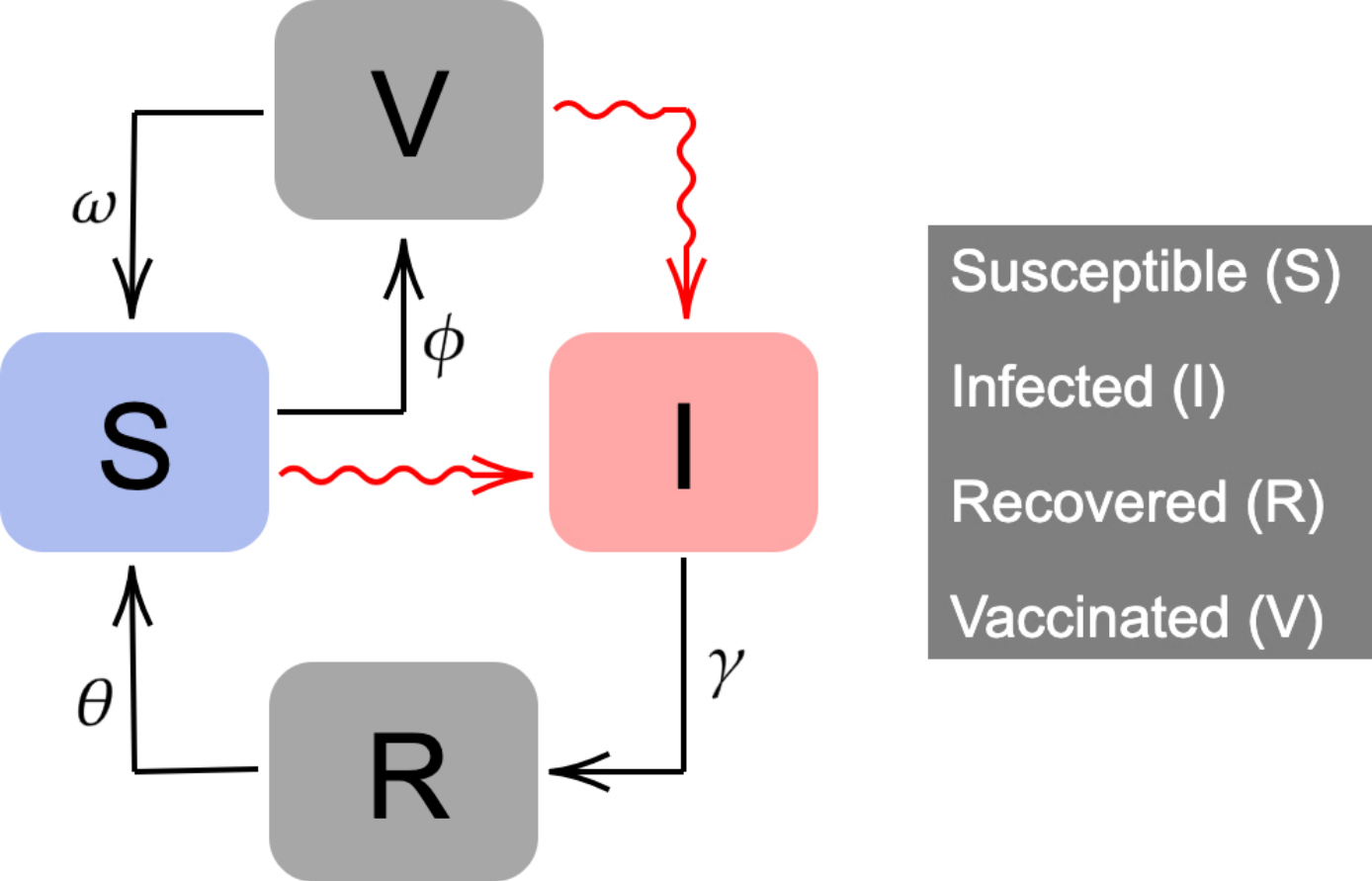
We propose an extension of the classic Kermack-McKendrick mathematical model. 𝑁(𝑡) is constant and is split into four compartments:
- susceptible (𝑆(𝑡)),
- infected (𝐼(𝑡)),
- recovered (𝑅(𝑡)),
- and vaccinated (𝑉 (𝑡)).
Susceptible individuals can become infected when interacting with an infectious individual. After a period of time (1∕𝛾), infected people recover. Recovered people lose their natural immunity after a period of time 1∕𝜃.
C_k(t^*) = 1 - \left(1 - \frac{I(t^*)}{N(t^*)}\right)^k
Risk index
Another closely related index that has been used to monitor and evaluate the development of ARI is the event gathering risk, developed by Chande (2020).
Chande, A., Lee, S., Harris, M. et al. Real-time, interactive website for US-county-level COVID-19 event risk assessment. at Hum Behav, 1313–1319 (2020). https://doi.org/10.1038/s41562-020-01000-9
Objective
Present a model for designing and evaluating light-traffic epidemic policies based on optimal control.
Outline
- Model Formulation:
- Risk Index and
- Functional Cost:Political economic implications
- Numerical experiments
- Perspectives
Objective and Outline
\begin{aligned}
S' =& \mu N - \lambda(t)S
- (\phi + \mu) S + \omega V + \theta R
\\
I' =& \lambda(t) (S + (1 - \sigma)V)
- (\gamma + \mu) I
\\
V' =& \phi S - (1 - \sigma) \lambda(t)V - (\omega + \mu) V
\\
R' =& \gamma I - (\theta + \mu) R
\end{aligned}
\begin{aligned}
C^{\prime} =& k (1 - C)^{\left(1 - \frac{1}{k}\right)}
\left(1 - (1 - C)^{\frac{1}{k}}\right)
\\
& \times
\left(
\beta(t) (1 - C(t))
(S + (1 - \sigma)V) \frac{1}{N} - (\gamma + \mu)
\right).
\end{aligned}
\begin{aligned}
\beta(t) & =
\left(
1 +
a \cos
\left(
\frac{2\pi}{365} t
\right)
\right) \beta_0
\\
\lambda(t) & = \beta(t) (1 - C(t)) \frac{I(t)}{N}
\end{aligned}
# MODEL FORMULATION
C(t) = 1 - \left(1 - \frac{I(t)}{N}\right)^k
Risk index
gives the probability of finding at time t an infected person in a group of k individuals.
\begin{aligned}
C' =& k (1 - C)^{\left(1 - \frac{1}{k}\right)}
\left(1 - (1 - C)^{\frac{1}{k}}\right)
\\
&
\times
\left(
\beta(t) (1 - C(t))
(S + (1 - \sigma)V) \frac{1}{N} - (\gamma + \mu)
\right)
\end{aligned}
\begin{aligned}
x^{\prime} &= \mu - \hat{\lambda}(t)x - (\phi + \mu) x + \omega v + \theta z
\\
y^{\prime} &= \hat{\lambda}(t) (x + (1 - \sigma)v) - (\gamma + \mu) y
\\
v^{\prime} &= \phi x - (1 - \sigma) \hat{\lambda}(t)v - (\omega + \mu) v
\\
z^{\prime} &= \gamma y - (\theta + \mu) z
\\
C^{\prime} &= k (1 - C)^{\left(1 - \frac{1}{k}\right)}
\left(
1 - (1 - C)^{\frac{1}{k}}
\right)
\\
& \times
\left(
\beta(t) (1 - C(t)) (x + (1 - \sigma) v) - (\gamma + \mu)
\right)
\end{aligned}
# REPRODUCTIVE NUMBER
x = \frac{S}{N};
\quad y = \frac{I}{N};
\quad v = \frac{V}{N};
\quad z = \frac{R}{N}
Normalization
\begin{aligned}
\Omega =
\Big \{
&
(x, y, v, z, C)\in \mathbb{R}^5_+
:
\\
&
0\leq C\leq 1,
\\
&
0 \leq s,
\forall s \in \{x, v, y, z \},
\\
&
x + y + v + z = 1
\Big \}
\end{aligned}
Invariance
\mathcal{R}_0 = \frac{\beta_0(1 - C^*)(x^* + (1 - \sigma)v^*)}{(\gamma + \mu)}
Basic Reproductive number
\begin{aligned}
x^* &= \frac{\omega + \mu}{\phi + \omega + \mu}
\\
v^* &= \frac{\phi}{\phi + \omega + \mu}
\\
C^* &= 0
\end{aligned}
FDE
Effective reproduction number
\mathcal{R}_t = \frac{\beta(t)(1 - C(t))(x(t) + (1 - \sigma)v(t))}{(\gamma + \mu)}
# Light Traffic Policies and Optimal Control
\xi(t)^\top:= (s(t), y(t),v(t),z(t), C(t))
\xi(t_0) \xrightarrow{\varphi}
A(\xi):= \Big \{green, yellow, orange, red \Big\}
(u_{\beta}^{4}, u_k^{4})
(u_{\beta}^{1}, u_k^{1})
(u_{\beta}^{3}, u_k^{3})
(u_{\beta}^{2}, u_k^{2})
- A decision-maker can apply a strategy from a finite set of actions.
- The set of actions implies a particular effect accordingly to the light semaphore.
- We describe this effect by modulating the transmission rate and size of gathering :
\beta(t),\ k.
- A decision-maker can apply a strategy from a finite set of actions.
- The set of actions implies a particular effect accordingly to the light semaphore.
- We describe this effect by modulating the transmission rate and size of gathering.
\begin{aligned}
\widehat{\lambda}(u_{\beta}, T_j):=
&
\beta(t)(1 - u_{\beta}) (1 - C(t)) y(t)
\\
k(u_k, T_j):=
& (1 - u_k) k
\end{aligned}
\begin{aligned}
x^{\prime} =&
\mu - \widehat{\lambda}(u_{\beta}, t) x - (\phi + \mu) x + \omega v + \theta z
\\
y^{\prime} =&
\widehat{\lambda}(u_{\beta}, t) (x + (1 - \sigma)v) - (\gamma + \mu) y
\\
v^{\prime} =&
\phi x - (1 - \sigma)
\widehat{\lambda}(u_{\beta}, t) v - (\omega + \mu) v
\\
z^{\prime} =&
\gamma y - (\theta + \mu) z
\\
C^{\prime} =&
k(u_k, T_j)
(1 - C) ^ {
\left(
1 - \frac{1}{k(u_k, T_j)}
\right)
}
\left(
1 - (1 - C) ^ \frac{1}{k(u_k, T_j)}
\right)
\\
& \times
\left[
\beta(t) (1 - u_{\beta}) (1 - C(t)) (x + (1 - \sigma) v)
- (\gamma + \mu)
\right]
\end{aligned}
T_i
T_{i+1}
T_{i-1}
\overbrace{\text{decision period}}^{p_j := t_j - t_{j-1}}
\underset{
\substack{
j \in A \\
A:=\{\text{green, yellow, orange, red} \}
}
}
%}
{
J
\left(
\xi^{[p_i]}, u_{\beta} ^{[j]}, u_k^{[j]}
\right)
}
:=
\underbrace{
\int_{0}^T
a_I y(s)
}_{YLD}
ds
+
\underbrace{
\int_{0}^T
a_C C(s)
+
a_{\beta} u_{\beta}^2(s)
+
a_k u_k^2(s)
}_{
\substack{
\text{political and economic}
\\
\text{implications}
}
}
ds.
\beta \rightsquigarrow \beta (1 -u_{\beta})
k \rightsquigarrow k (1 - u_{k})
\underset{
\substack{
j \in A \\
A:=\{\text{green, yellow, orange, red} \}
}
}
%}
{
J
\left(
\xi^{[p_i]}, u_{\beta} ^{[j]}, u_k^{[j]}
\right)
}
:=
\underbrace{
\int_{0}^T
a_I y(s)
}_{YLD}
ds
+
\underbrace{
\int_{0}^T
a_C C(s) +
a_{\beta} u_{\beta}^2(s)
+
a_k u_k^2(s)
}_{
\substack{
\text{political and economic}
\\
\text{implications}
}
}
ds.
- The decision maker only chooses the strategy from a finite set of actions--as mentioned above-- and according to the light traffic protocol. Thus, the controller decides which color from the plausible light-traffic actions for the next period.
- The corresponding authorities periodically meet every few weeks and make a decision.
- The decision taken minimizes the functional J subject to the mentioned dynamics.
Hypothesis
T_i
T_{i+1}
T_{i-1}
\overbrace{\text{decision period}}^{p_j := t_j - t_{j-1}}
(OCP) Decide in each stage (a week), the light color that minimize functional cost J
\begin{aligned}
\beta(t) := &
\left(
1 +
a \cos
\left(
\frac{2\pi}{365} t
\right)
\right) \beta_0
\\
\widehat{\lambda}(u_{\beta}, t_j):=
&
\beta(t)(1 - u_{\beta}) (1 - C(t)) y(t)
\\
k(u_k, t_j):=
& (1 - u_k) k
\end{aligned}
\begin{aligned}
x^{\prime} =&
\mu - \widehat{\lambda}(u_{\beta}, t) x - (\phi + \mu) x + \omega v + \theta z
\\
y^{\prime} =&
\widehat{\lambda}(u_{\beta}, t) (x + (1 - \sigma)v) - (\gamma + \mu) y
\\
v^{\prime} =&
\phi x - (1 - \sigma)
\widehat{\lambda}(u_{\beta}, t) v - (\omega + \mu) v
\\
z^{\prime} =&
\gamma y - (\theta + \mu) z
\\
C^{\prime} =&
k(u_k, t_j)
(1 - C) ^ {
\left(
1 - \frac{1}{k(u_k, t_j)}
\right)
}
\left(
1 - (1 - C) ^ \frac{1}{k(u_k, t_j)}
\right)
\\
& \times
\left[
\beta(t) (1 - u_{\beta}) (1 - C(t)) (x + (1 - \sigma) v)
- (\gamma + \mu)
\right]
\end{aligned}
\underset{
\substack{
j \in A \\
A:=\{\text{green, yellow, orange, red} \}
}
}
{
\min
}
J
\left(
\xi^{[p_i]},
u_{\beta} ^ {[j]},
u_k ^ {[j]}
\right)
:=
\underbrace{
\int_{T_{i-1}} ^ {T_{i}}
a_I y(s)
}_{YLD}
ds
+
\underbrace{
\int_{T_{i-1}} ^{T_{i}}
a_C C(s) +
a_{\beta} u_{\beta}^2(s)
+
a_k u_k ^ 2(s)
}_{
\substack{
\text{political and economic}
\\
\text{implications}
}
} ds.
subject to:
Counterfactual vs controlled dynamics
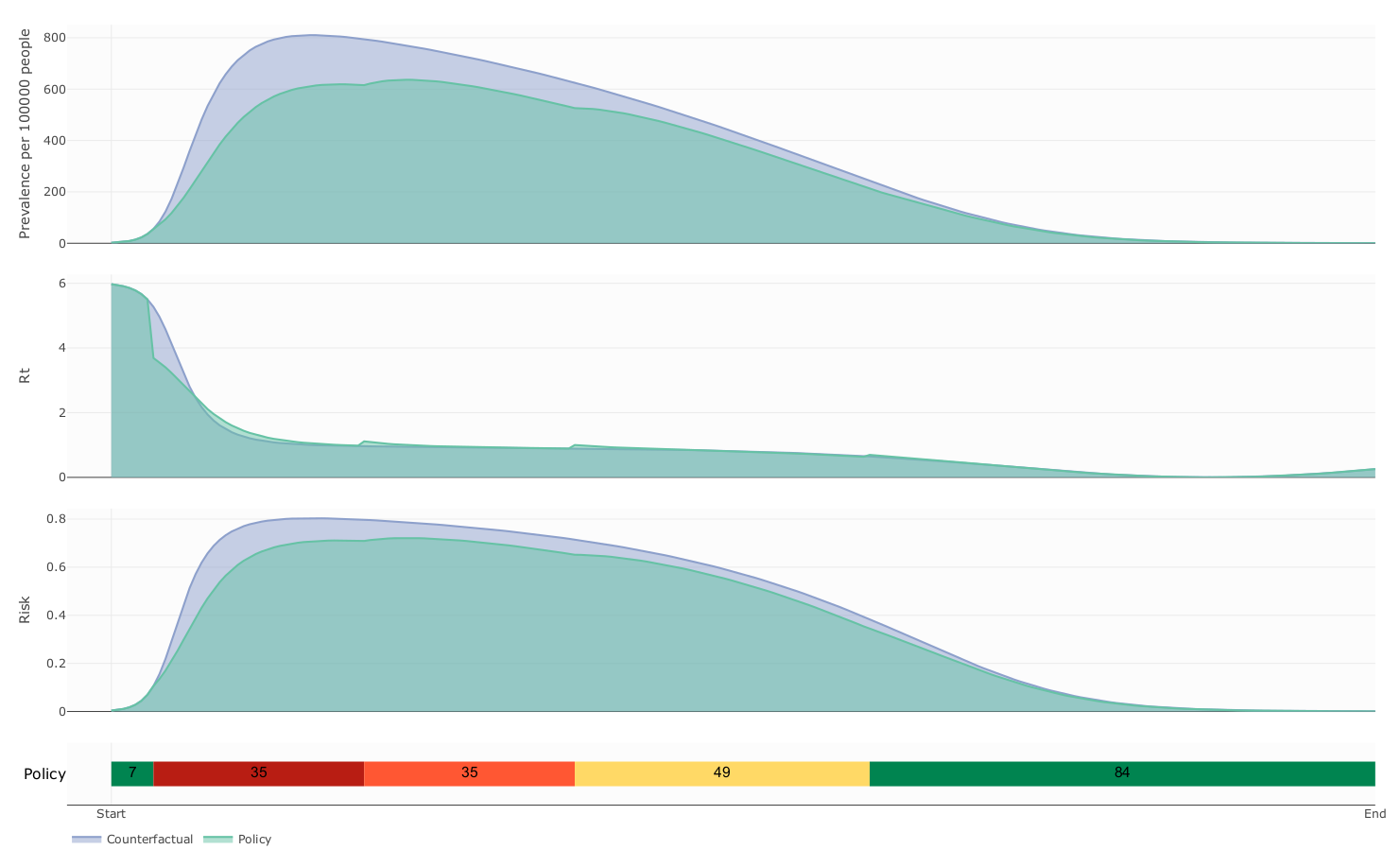
Counterfactual vs controlled dynamics
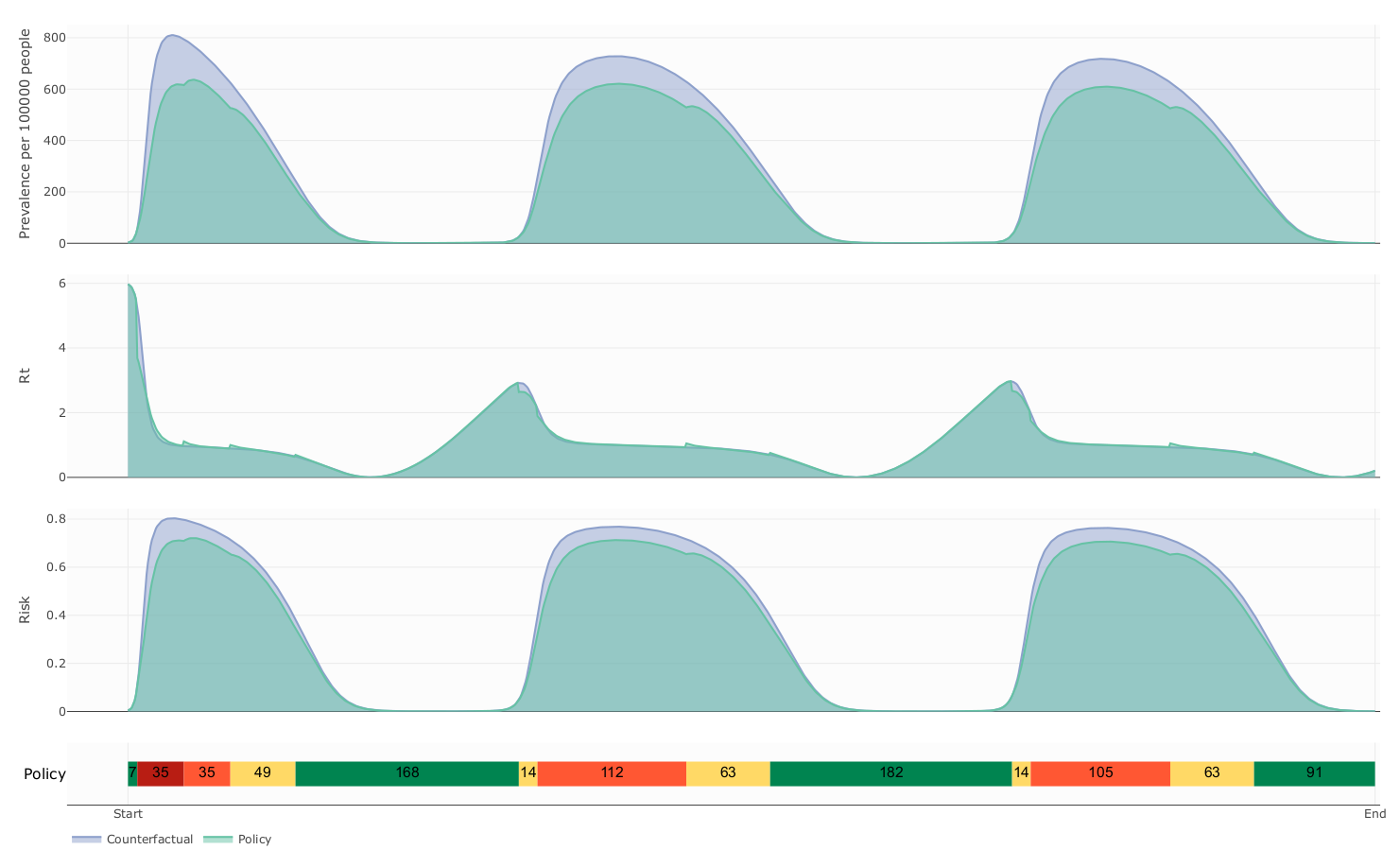
Counterfactual vs controlled dynamics
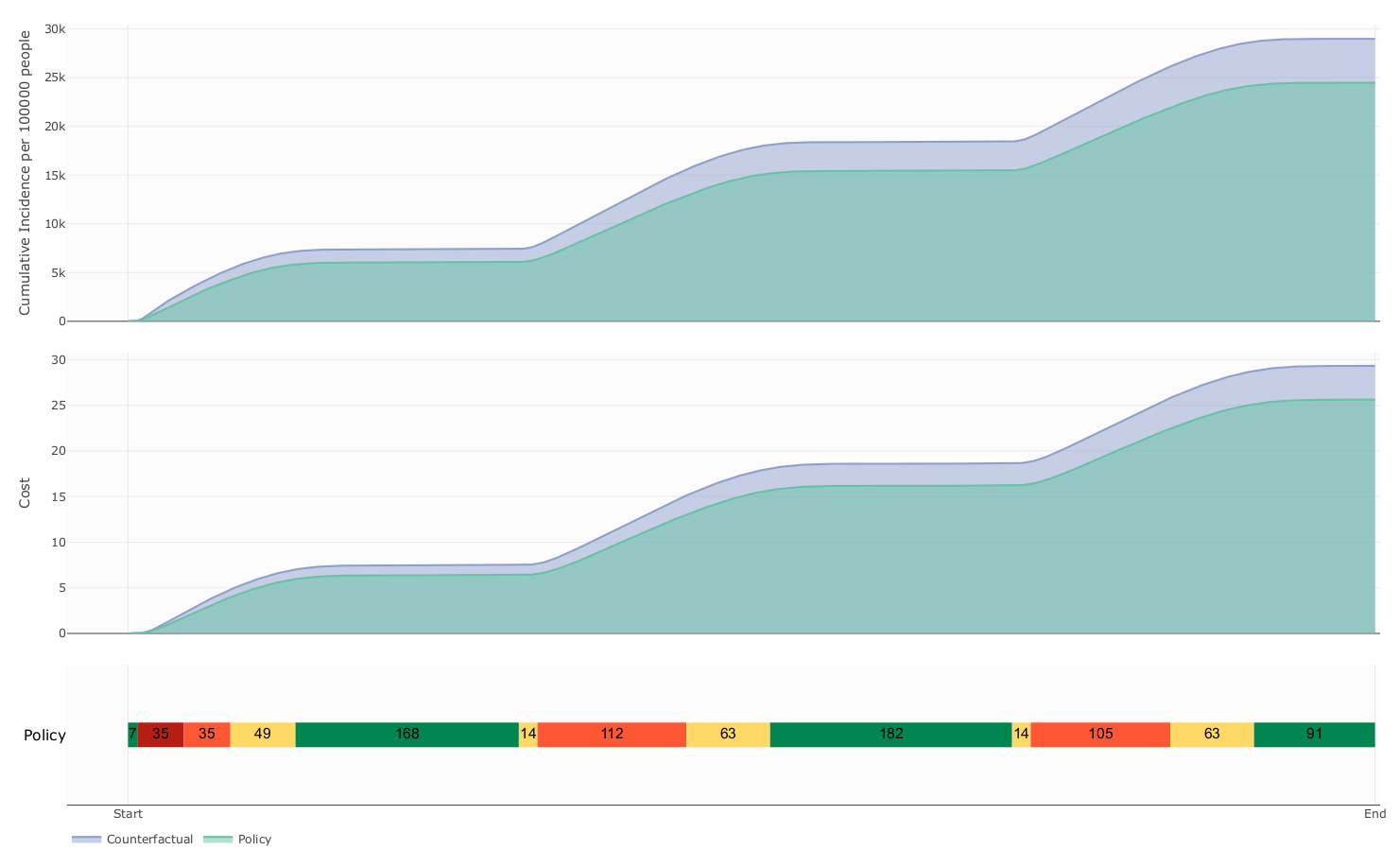
The influence of mobility restriction expenses over prevalence and cost
\underset{
\substack{
j \in A \\
A:=\{\text{green, yellow, orange, red} \}
}
}
{
J
\left(
\xi^{[p_i]},
u_{\beta} ^ {[j]},
u_k ^ {[j]}
\right)
}
:=
%
\int_{T_{i-1}} ^ {T_{i}}
a_I y(s) + a_C C(s)
ds
+
\int_{T_{i-1}} ^{T_{i}}
a_{\beta}
u_{\beta}^2(s)
+
a_k u_k ^ 2(s)
ds.
Expenses
due to mobility restrictions
a_{\beta} \searrow
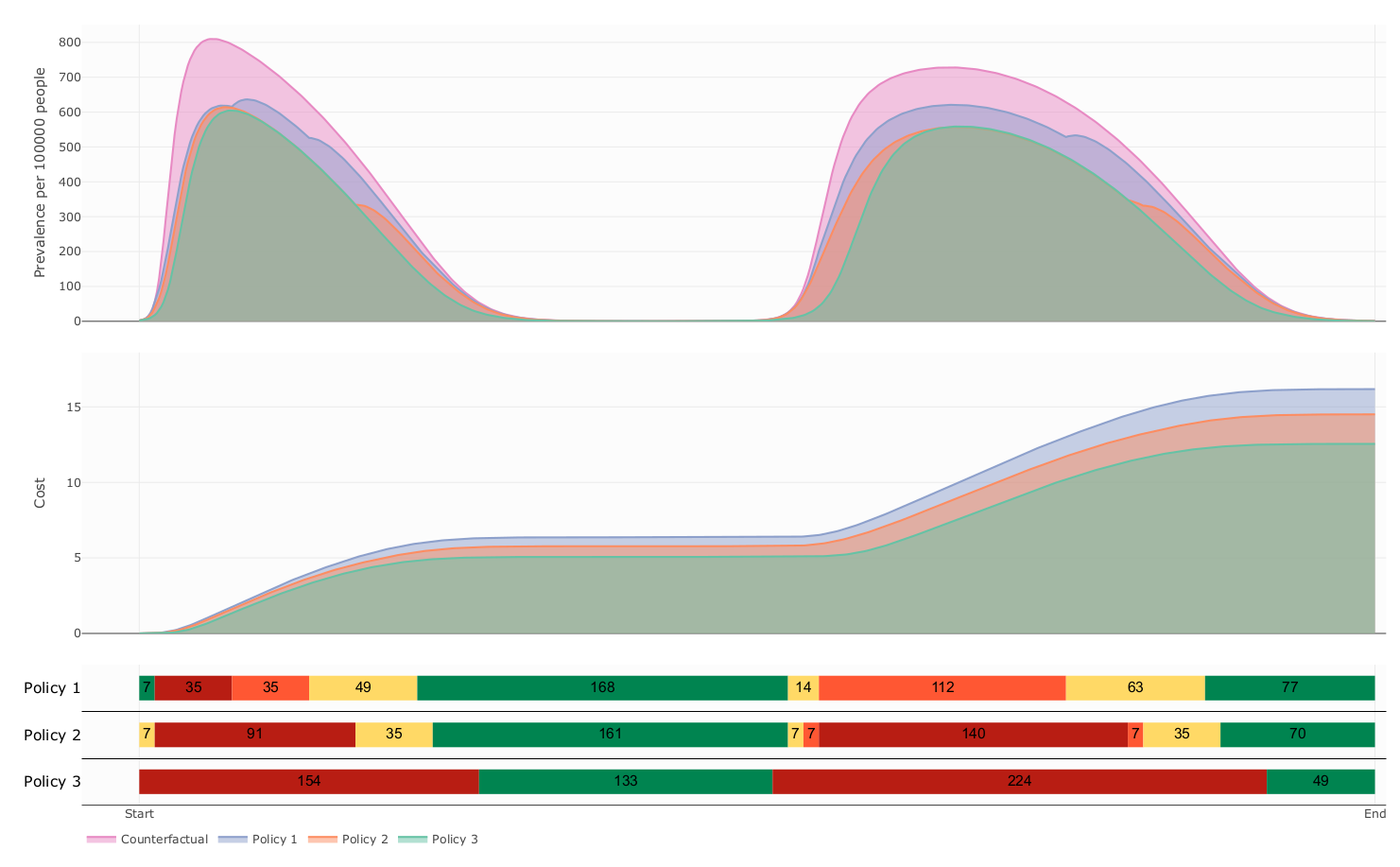
The influence of decision period span over prevalence and cost
\underset{
\substack{
j \in A \\
A:=\{\text{green, yellow, orange, red} \}
}
}
{
J
\left(
\xi^{[p_i]},
u_{\beta} ^ {[j]},
u_k ^ {[j]}
\right)
}
:=
%
\int_{T_{i-1}} ^ {T_{i}}
a_I y(s) + a_C C(s)
ds
+
\int_{T_{i-1}} ^{T_{i}}
a_{\beta}
u_{\beta}^2(s)
+
a_k u_k ^ 2(s)
ds.
\underbrace{p_i:=T_{i+1} - T_i}_{\substack{decision \\ period}}
p_i \nearrow
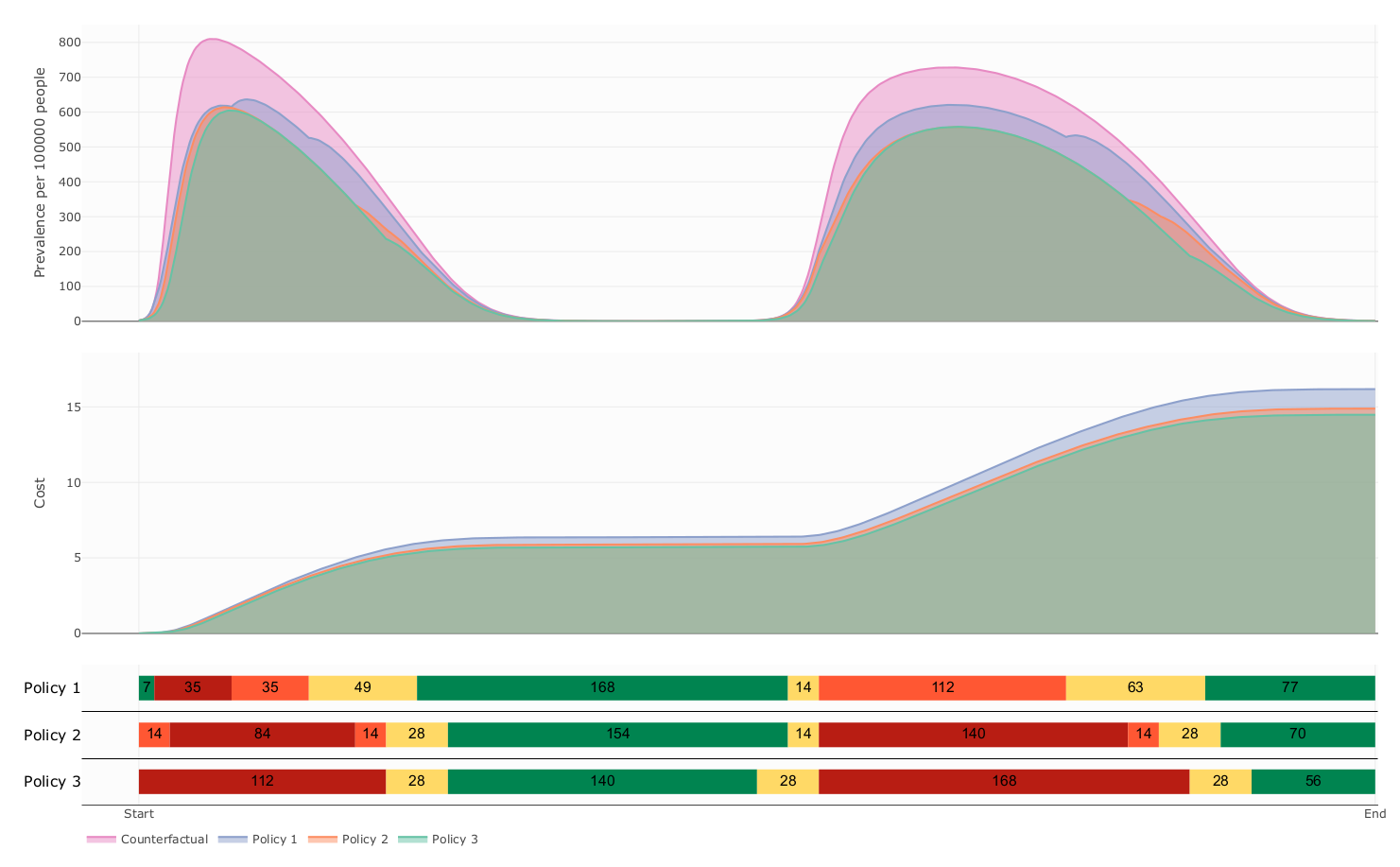
- Our model suggest that this kind of Policies follows a delicate balanced between health benefit and economic cost
Perspectives
- Uncertainty quantification
- Partial information
- Games
References
- Chande, A., Lee, S., Harris, M. et al. Real-time, interactive website for US-county-level COVID-19 event risk assessment. Nat Hum Behav 4, 1313–1319 (2020). https://doi.org/10.1038/s41562-020-01000-9
- Chan, H.F., Skali, A., Savage, D.A. et al. Risk attitudes and human mobility during the COVID-19 pandemic. Sci Rep 10, 19931 (2020). https://doi.org/10.1038/s41598-020-76763-2
- P. van den Driessche, James Watmough, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission, Mathematical Biosciences, Volume 180, Issues 1–2, 2002,Pages 29-48,ISSN 0025-5564, https://doi.org/10.1016/S0025-5564(02)00108-6.
https://slides.com/sauldiazinfantevelasco/code
https://www.medrxiv.org/content/10.1101/2022.12.16.22283591v1
ASU-MathBioFeb-18-2023
By Saul Diaz Infante Velasco
ASU-MathBioFeb-18-2023
Slides for the Math Bio seminar of ASU
