Lecture 6: Neural Networks
Shen Shen
Oct 4, 2024
Intro to Machine Learning
Outline
- Recap, the leap from simple linear models
- (Feedforward) Neural Networks Structure
- Design choices
- Forward pass
- Backward pass
- Back-propagation
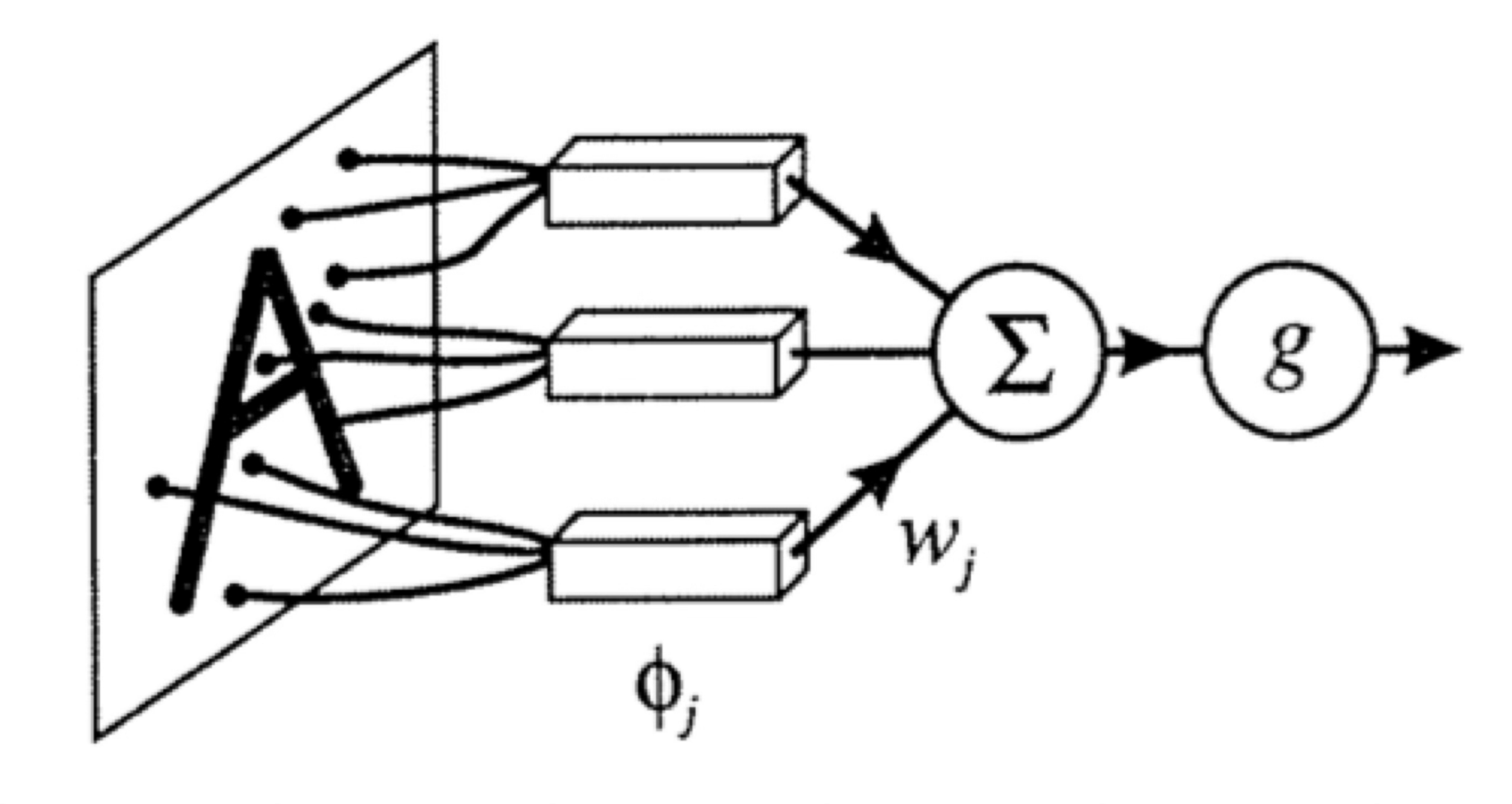
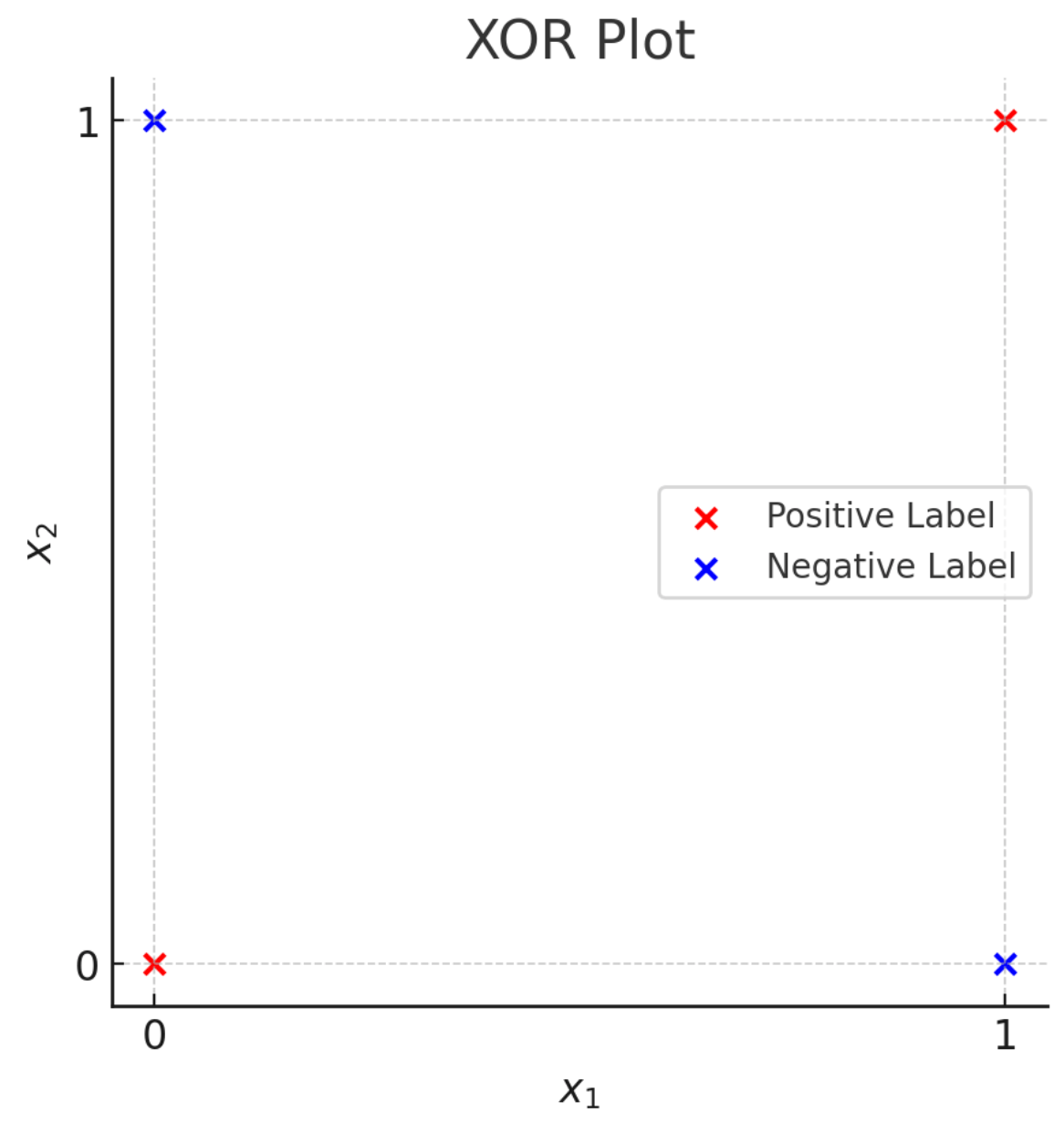
Recap:
leveraging nonlinear transformations
👆
importantly, linear in \(\phi\), non-linear in \(x\)
\phi\left(\left[x_1; x_2\right]\right)=\left[1;|x_1-x_2|\right]
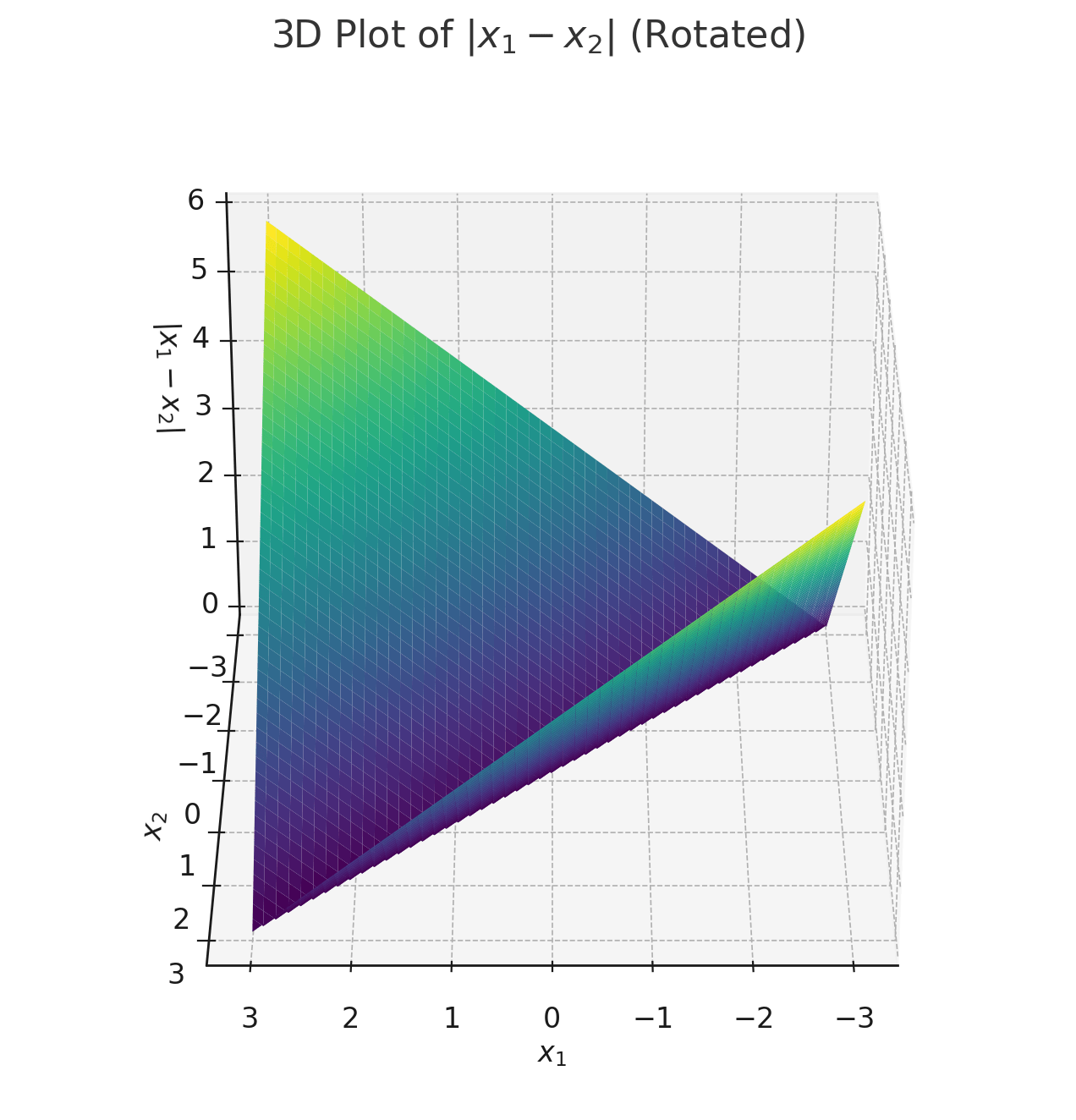
transform via
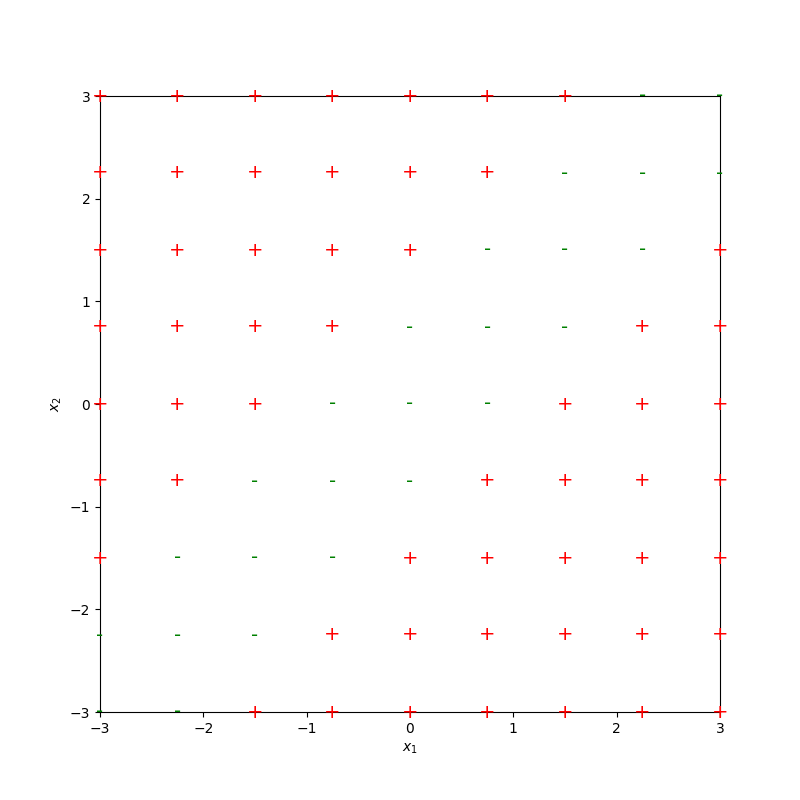
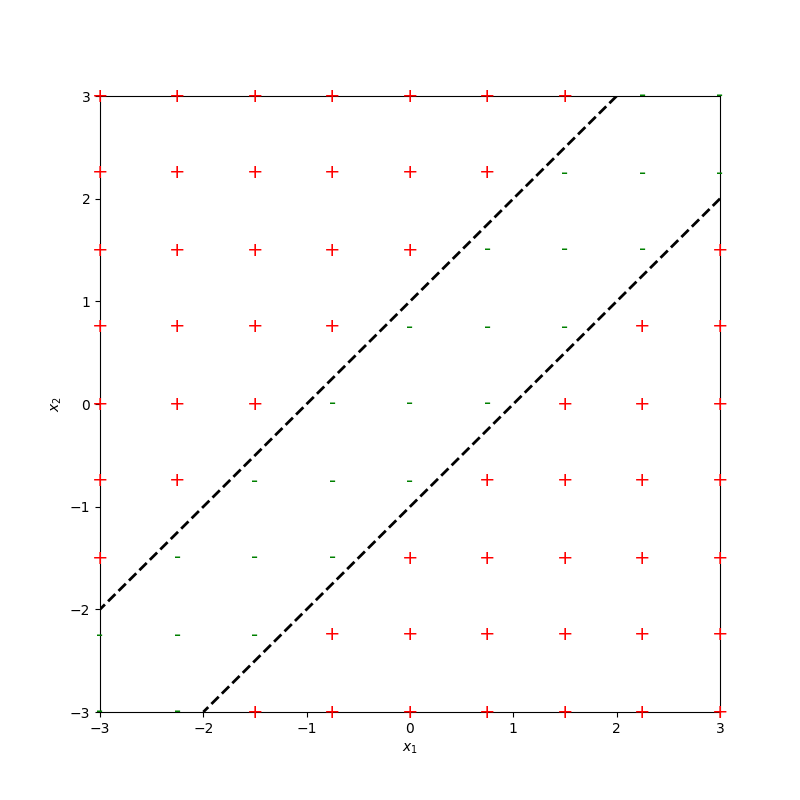
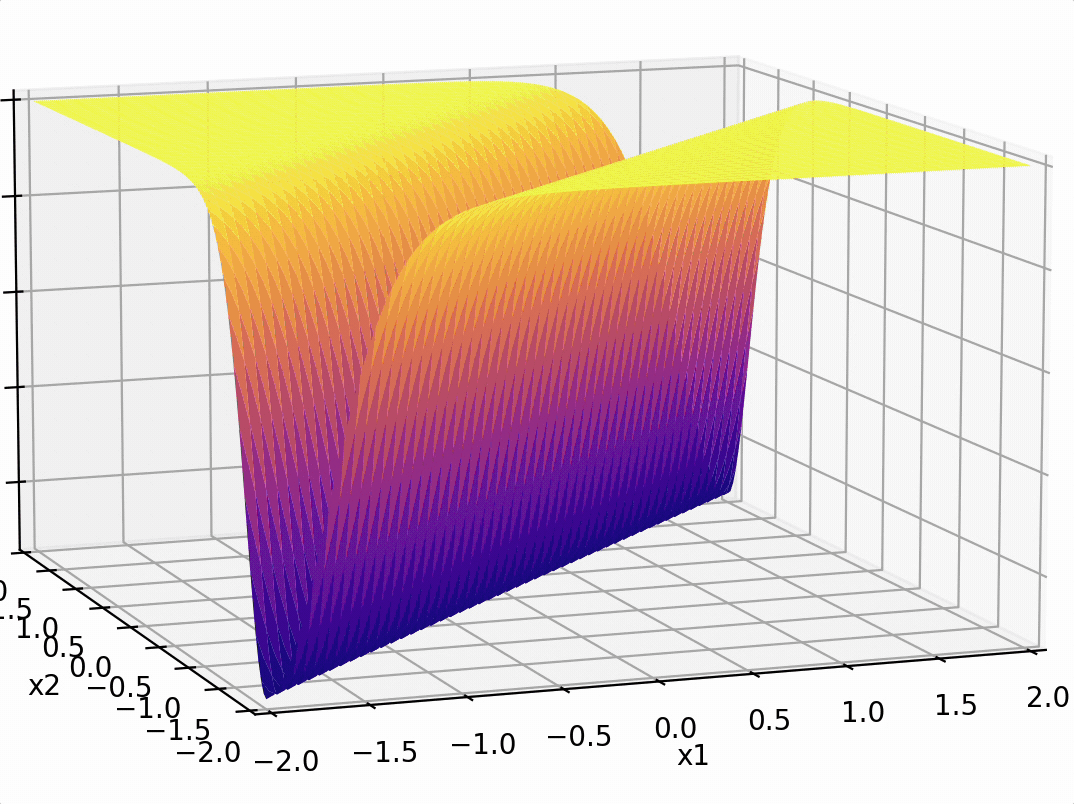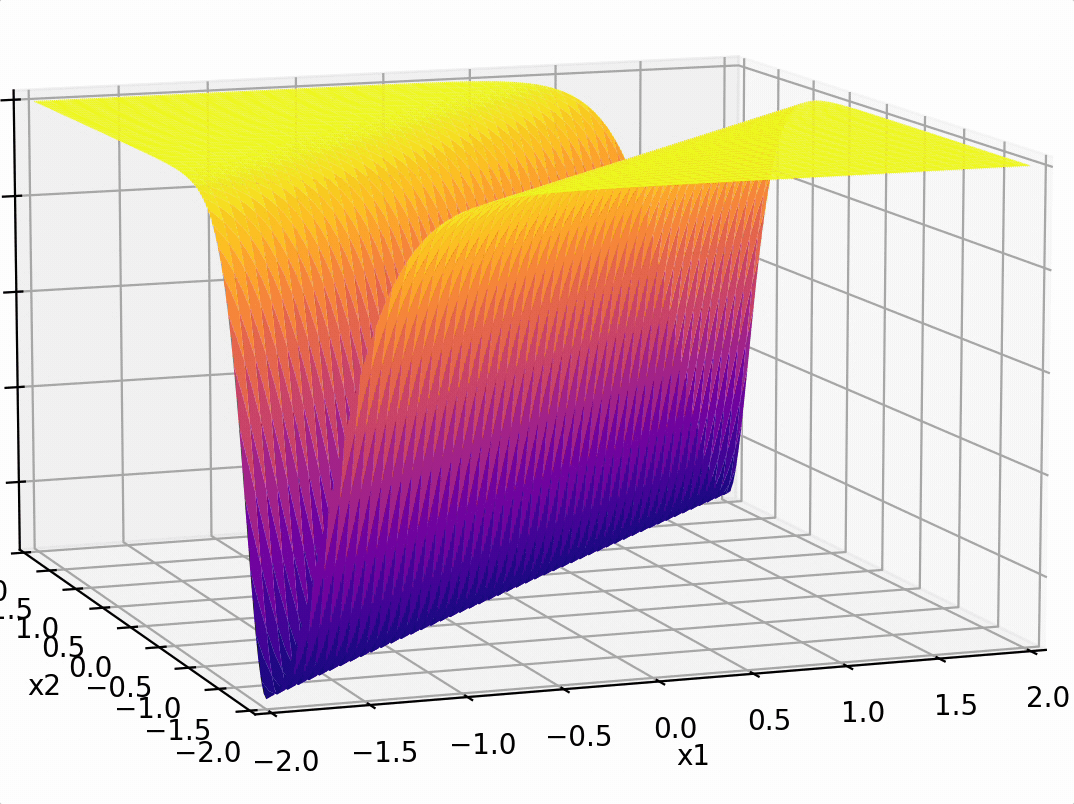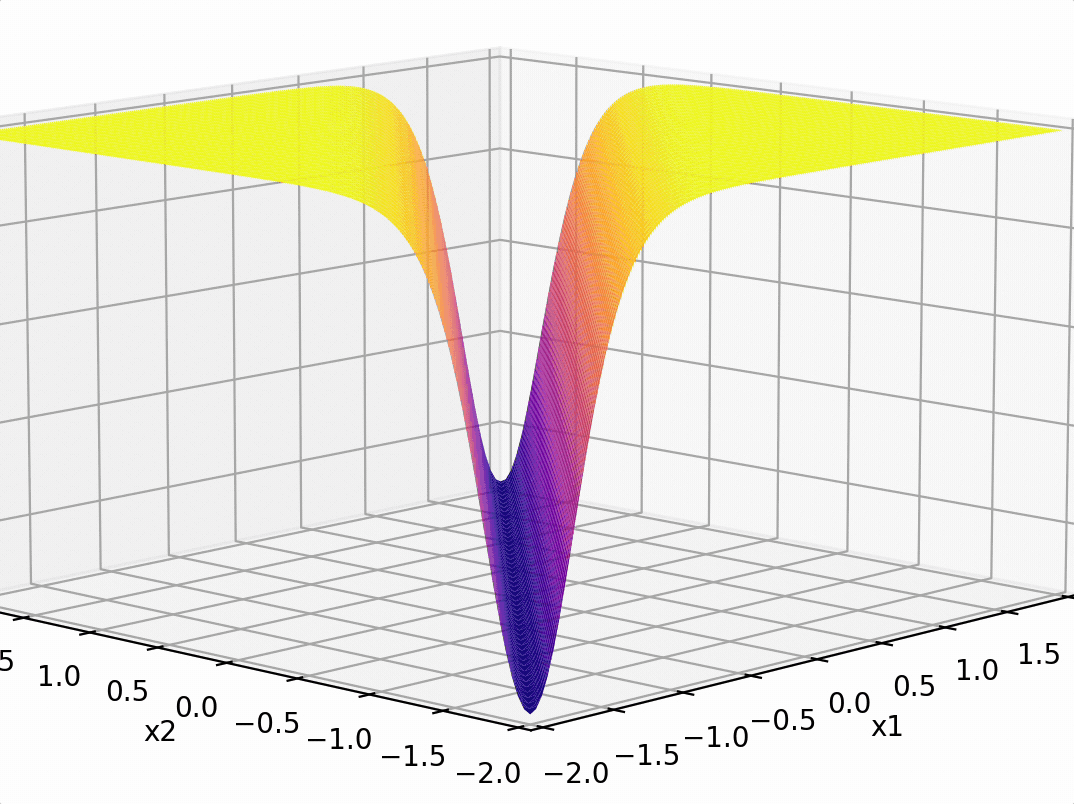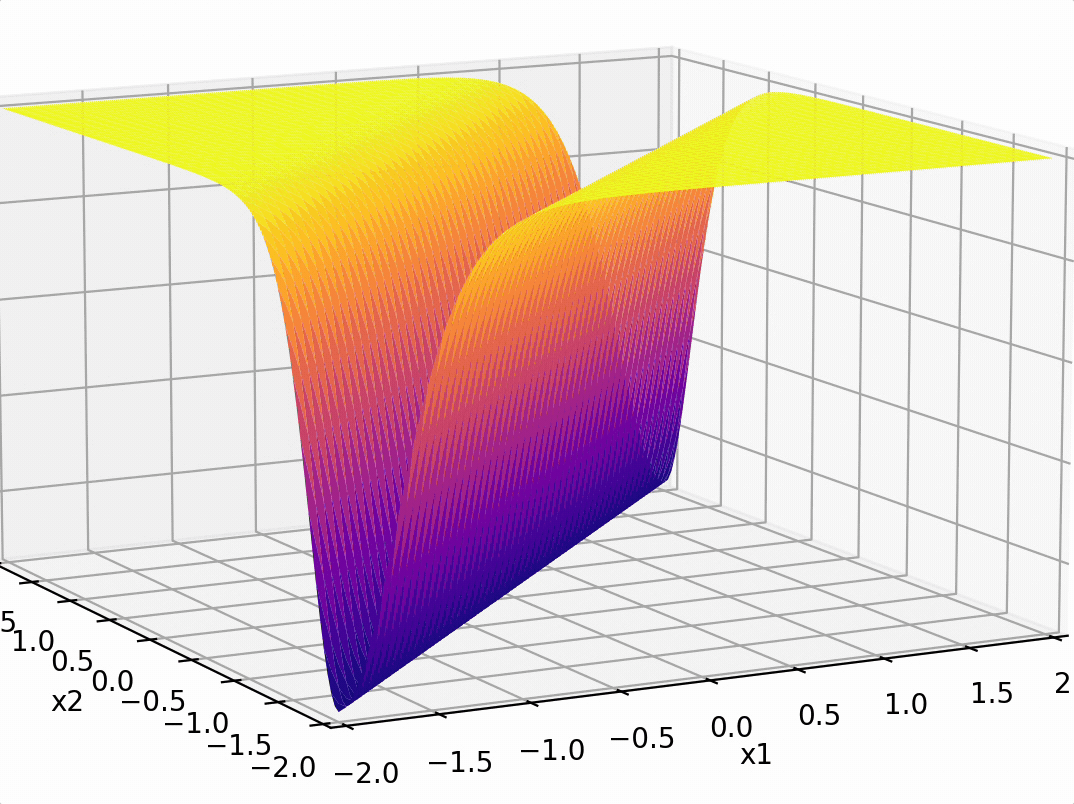
Pointed out key ideas (enabling neural networks):
- Nonlinear feature transformation
- "Composing" simple transformations
- Backpropagation
\}
expressiveness
efficient training
\sigma_1 = \sigma(5 x_1 -5 x_2 + 1)
\sigma_2 = \sigma(-5 x_1 + 5 x_2 + 1)
Two epiphanies:
- nonlinear transformation empowers linear tools
- "composing" simple nonlinearities amplifies such effect
some appropriate weighted sum
Outline
- Recap, the leap from simple linear models
-
(Feedforward) Neural Networks Structure
- Design choices
- Forward pass
- Backward pass
- Back-propagation
👋 heads-up, in this section, for simplicity:
all neural network diagrams focus on a single data point
A neuron:
\(w\): what the algorithm learns
- \(x\): \(d\)-dimensional input
a = f(z)
\Sigma
A neuron:
- \(a\): post-activation output
- \(f\): activation function
- \(w\): weights (i.e. parameters)
- \(z\): pre-activation output
\(f\): what we engineers choose
\dots
x_1
x_2
x_d
x = \left[ \begin{array}{c}
\\
\\
\\
\\
\\
\\
\\
\end{array} \right]
w_1
w_d
\dots
w_2
= w^Tx
z
f(\cdot)
= f(w^Tx)
\(z\): scalar
\(a\): scalar
Choose activation \(f(z)=z\)
learnable parameters (weights)
e.g. linear regressor represented as a computation graph
= z
= w^Tx
w_1
w_d
\dots
x_1
x_2
x_d
\dots
x = \left[ \begin{array}{c}
\\
\\
\\
\\
\\
\\
\\
\end{array} \right]
w_2
\Sigma
f(\cdot)
g
z
Choose activation \(f(z)=\sigma(z)\)
learnable parameters (weights)
e.g. linear logistic classifier represented as a computation graph
= \sigma(z)
= w^Tx
w_1
w_d
\dots
x_1
x_2
x_d
\dots
w_2
\Sigma
f(\cdot)
g
z
x = \left[ \begin{array}{c}
\\
\\
\\
\\
\\
\\
\\
\end{array} \right]
\dots
A layer:
learnable weights
A layer:
a^1
z^1
\Sigma
f(\cdot)
z^2
\Sigma
f(\cdot)
a^2
z^m
a^m
\Sigma
f(\cdot)
\dots
x_1
x_2
x_d
- (# of neurons) = (layer's output dimension).
- typically, all neurons in one layer use the same activation \(f\) (if not, uglier algebra).
- typically fully connected, where all \(x_i\) are connected to all \(z_j,\) meaning each \(x_i\) influences every \(a_j\) eventually.
- typically, no "cross-wiring", meaning e.g. \(z_1\) won't affect \(a^2.\) (the final layer may be an exception if softmax is used.)
\dots
layer
linear combo
activations
A (fully-connected, feed-forward) neural network:
\dots
\dots
layer
\dots
x_1
x_2
x_d
input
\Sigma
f(\cdot)
\Sigma
f(\cdot)
\Sigma
f(\cdot)
\Sigma
f(\cdot)
\Sigma
f(\cdot)
\Sigma
f(\cdot)
\Sigma
f(\cdot)
neuron
learnable weights
We choose:
- activation \(f\) in each layer
- # of layers
- # of neurons in each layer
hidden
output
Outline
- Recap, the leap from simple linear models
- (Feedforward) Neural Networks Structure
- Design choices
- Forward pass
- Backward pass
- Back-propagation
\sigma_1 = \sigma(5 x_1 + -5 x_2 + 1)
\sigma_2 = \sigma(-5 x_1 + 5 x_2 + 1)
some appropriate weighted sum
recall this example
x_1
x_2
1
\Sigma
f(\cdot)
\Sigma
f(\cdot)
\Sigma
f(\cdot)
\(f(\cdot) = \sigma(\cdot)\)
\(f(\cdot) \) identity function
it can be represented as
Activation function \(f\) choices
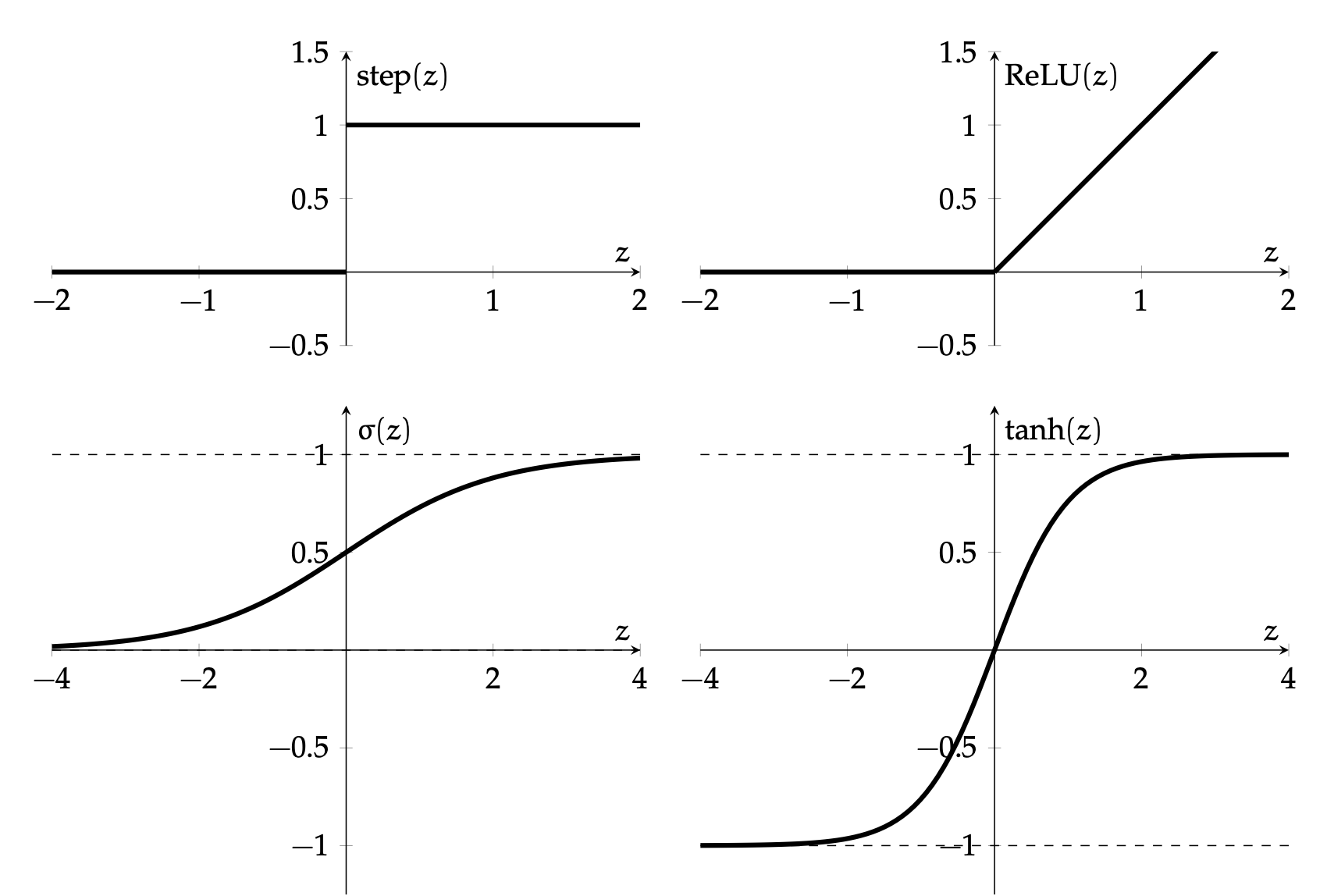
\(\sigma\) used to be the most popular
- firing rate of a neuron
- elegant gradient \(\sigma^{\prime}(z)=\sigma(z) \cdot(1-\sigma(z))\)
a = f(z)
\Sigma
\dots
x_1
x_2
x_d
x = \left[ \begin{array}{c}
\\
\\
\\
\\
\\
\\
\\
\end{array} \right]
w_1
w_d
\dots
w_2
= w^Tx
z
f(\cdot)
= f(w^Tx)
- default choice in hidden layers
- very simple function form, so is the gradient.
\operatorname{ReLU}(z)=\left\{\begin{array}{ll}
0 & \text { if } z<0 \\
z & \text { otherwise }
\end{array}\\
\\
\right.
=\max (0, z)
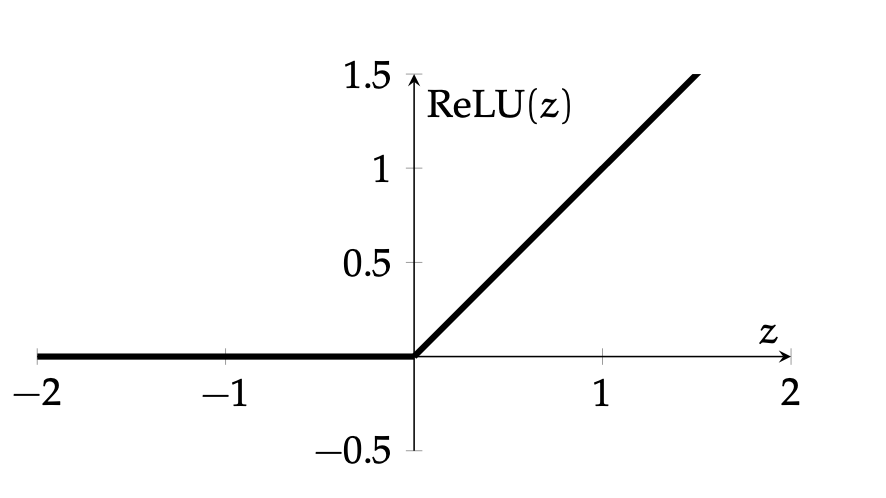
nowadays
- drawback: if strongly in negative region, a single ReLU can be "dead" (no gradient).
- Luckily, typically we have lots of units, so not everyone is dead.
\frac{\partial \text{ReLU}(z)}{\partial z}:=\left\{\begin{array}{lll}
0, & \text { if } \quad z<0 \\
1, & \text { if } \quad \text{otherwise}
\end{array}\right.
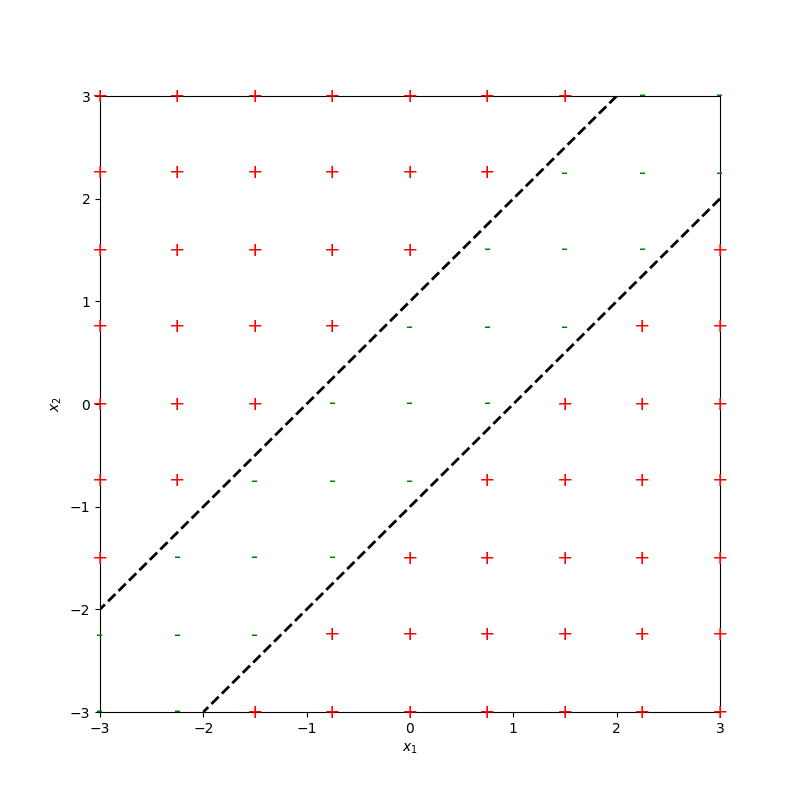
compositions of ReLU(s) can be quite expressive
in fact, asymptotically, can approximate any function!
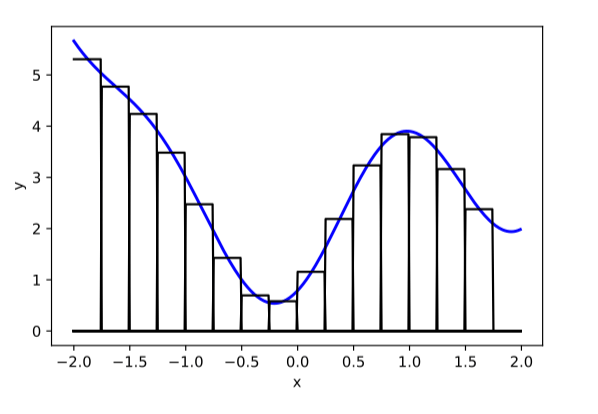
(image credit: Phillip Isola)
x_1
x_2
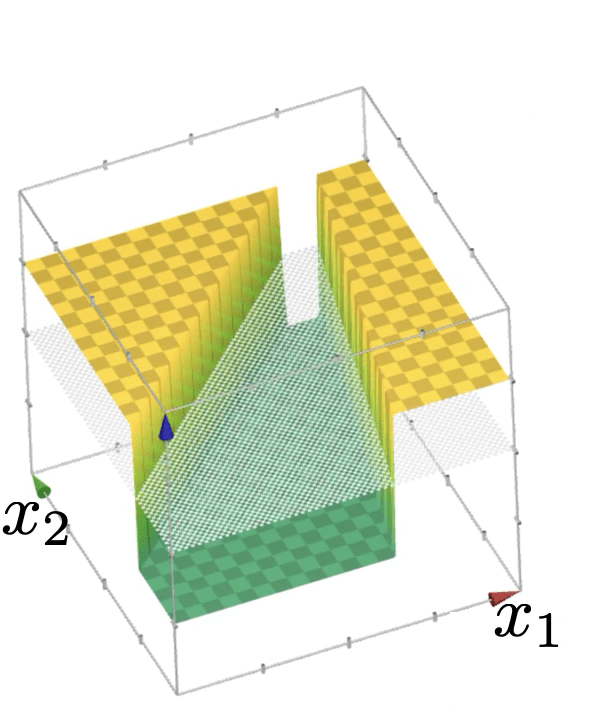
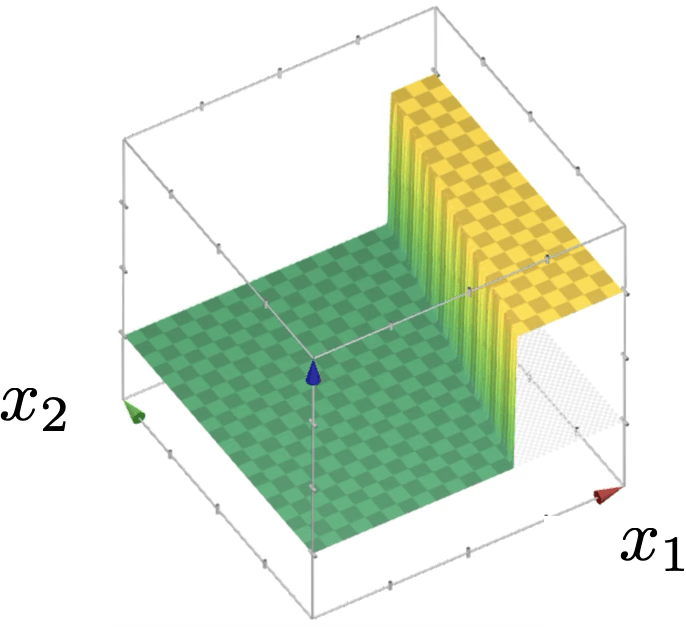
(image credit: Tamara Broderick)
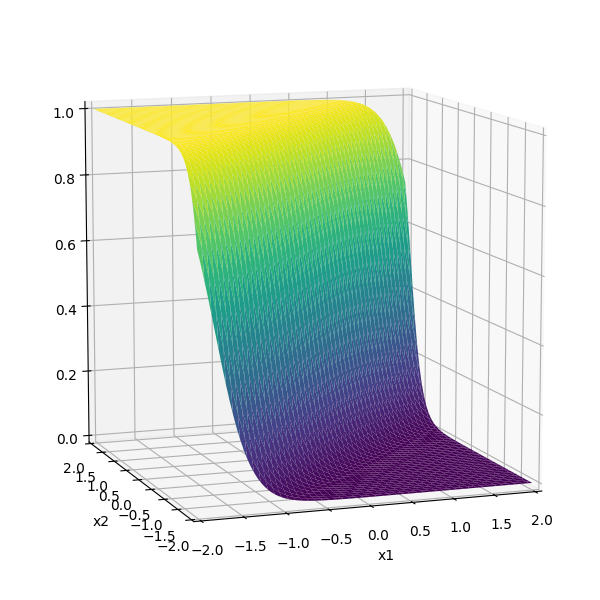
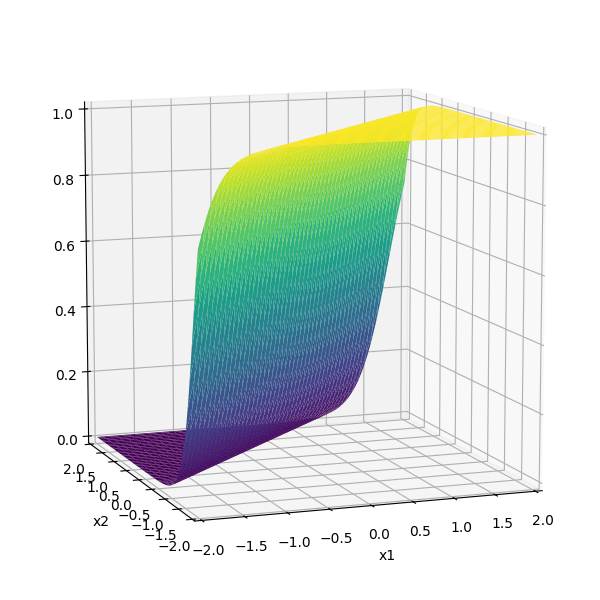
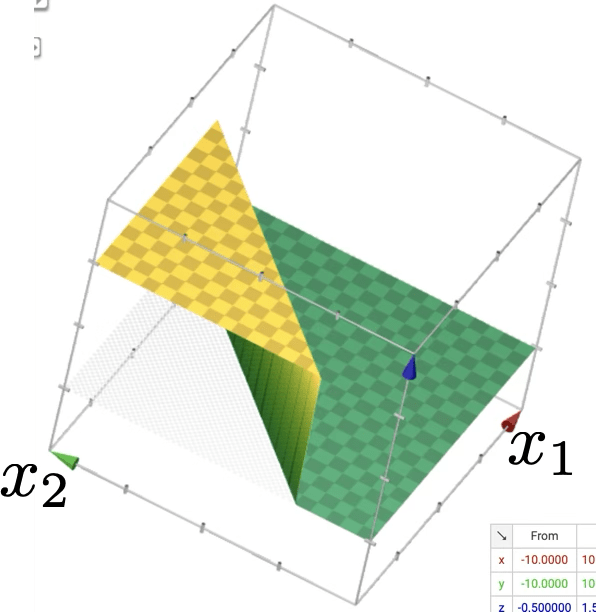
or give arbitrary decision boundaries!
+
=
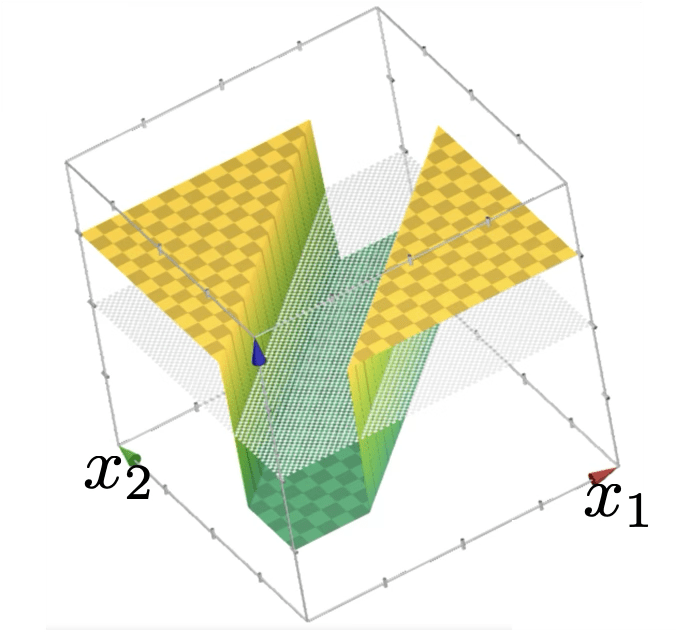
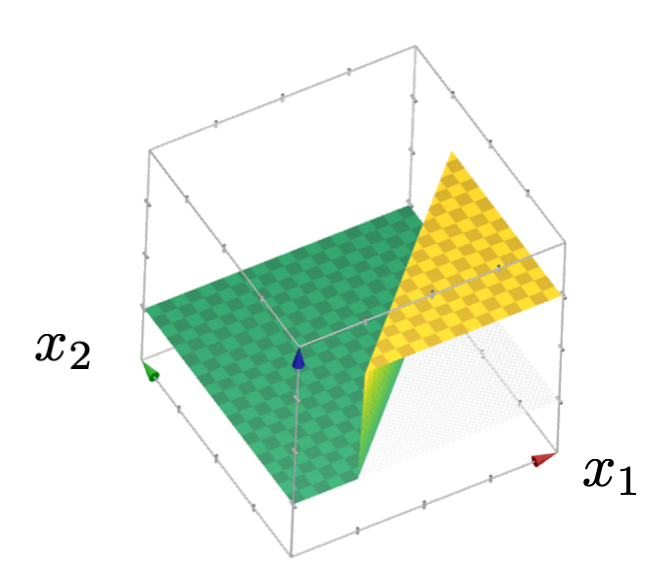
(image credit: Tamara Broderick)
+
=
output layer design choices
- # neurons, activation, and loss depend on the high-level goal.
- typically straightforward.
- Multi-class setup: if predict one and only one class out of \(K\) possibilities, then last layer: \(K\) neurons, softmax activation, cross-entropy loss
- other multi-class settings, see discussion in lab.
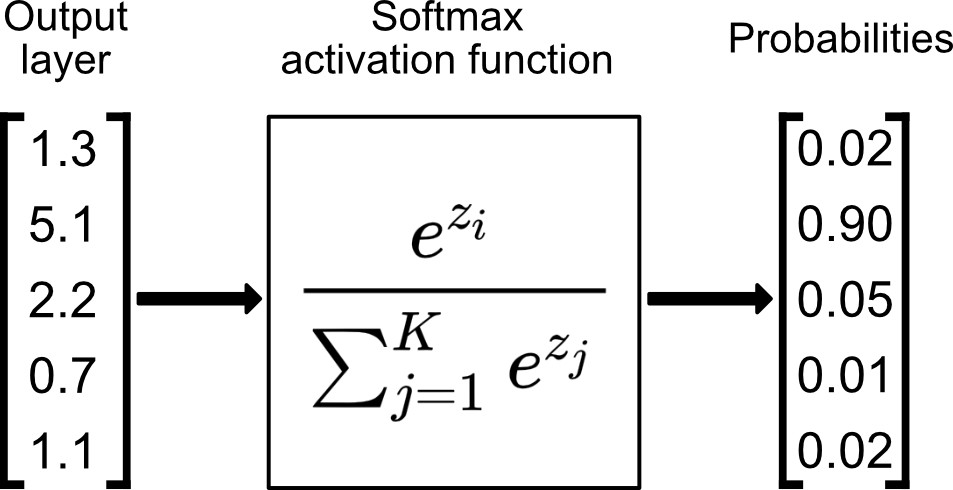
e.g., say \(K=5\) classes
input \(x\)
hidden layer(s)
\dots
output layer
- Width: # of neurons in layers
- Depth: # of layers
- More expressive if increasing either the width or depth.
- The usual pitfall of overfitting (though in NN-land, it's also an active research topic.)
(The demo won't embed in PDF. But the direct link below works.)
Outline
- Recap, the leap from simple linear models
- (Feedforward) Neural Networks Structure
- Design choices
- Forward pass
- Backward pass
- Back-propagation
- Evaluate the loss \(\mathcal{L} = (g-y)^2\)
- Repeat for each data point, average the sum of \(n\) individual losses
e.g. forward-pass of a linear regressor
y^{(i)}
f(\cdot)
\mathcal{L}(g, y)
\mathcal{L}(g, y)
\underbrace{\quad \quad \quad } \\ n
\mathcal{L}(g, y)
\dots
= w^Tx
w_1
w_d
\dots
w_2
\Sigma
z
= z
g
\dots
x_1
x_2
x_d
x^{(i)} \quad = \left[ \begin{array}{c}
\\
\\
\\
\\
\\
\\
\\
\end{array} \right]
\dots
\dots
- Evaluate the loss \(\mathcal{L} = - [y \log g+\left(1-y\right) \log \left(1-g\right)]\)
- Repeat for each data point, average the sum of \(n\) individual losses
f(\cdot)
\mathcal{L}(g, y)
\mathcal{L}(g, y)
\underbrace{\quad \quad \quad } \\ n
\mathcal{L}(g, y)
\dots
x_1
x_2
x_d
x^{(i)} \quad = \left[ \begin{array}{c}
\\
\\
\\
\\
\\
\\
\\
\end{array} \right]
= w^Tx
w_1
w_d
\dots
w_2
\Sigma
z
= \sigma(z)
g
e.g. forward-pass of a linear logistic classifier
\dots
y^{(i)}
\dots
\dots
x^{(1)}
y^{(1)}
f^1
linear combination
nonlinear activation
\begin{aligned}
& W^1 \\
\end{aligned}
\begin{aligned}
& W^2 \\
\end{aligned}
\begin{aligned}
& W^L \\
\end{aligned}
f^2
f^L
g^{(1)}
\(\dots\)
f^2\left(\hspace{2cm}; \mathbf{W}^2\right)
f^1(\mathbf{x}^{(i)}; \mathbf{W}^1)
f^L\left(\dots \hspace{3.5cm}; \dots \mathbf{W}^L\right)
Forward pass:
evaluate, given the current parameters,
- the model output \(g^{(i)}\) =
- the loss incurred on the current data \(\mathcal{L}(g^{(i)}, y^{(i)})\)
- the training error \(J = \frac{1}{n} \sum_{i=1}^{n}\mathcal{L}(g^{(i)}, y^{(i)})\)
\mathcal{L}(g^{(1)}, y^{(1)})
\mathcal{L}(g, y)
\mathcal{L}(g^{(n)}, y^{(n)})
\underbrace{\quad \quad \quad \quad \quad } \\ n
\dots
\dots
\dots
loss function
Outline
- Recap, the leap from simple linear models
- (Feedforward) Neural Networks Structure
- Design choices
- Forward pass
-
Backward pass
- Back-propagation
- Randomly pick a data point \((x^{(i)}, y^{(i)})\)
- Evaluate the gradient \(\nabla_{W^2} \mathcal{L(g^{(i)},y^{(i)})}\)
- Update the weights \(W^2 \leftarrow W^2 - \eta \nabla_{W^2} \mathcal{L(g^{(i)},y^{(i)}})\)
x^{(i)}
y^{(i)}
f^1
\begin{aligned}
& W^1 \\
\end{aligned}
\begin{aligned}
& W^2 \\
\end{aligned}
\begin{aligned}
& W^L \\
\end{aligned}
f^2
f^L
g^{(i)}
\(\dots\)
\mathcal{L}(g^{(i)}, y^{(i)})
\mathcal{L}(g, y)
\mathcal{L}(g^{(n)}, y^{(n)})
\underbrace{\quad \quad \quad \quad \quad } \\ n
\dots
\dots
\dots
Backward pass:
Run SGD to update the parameters, e.g. to update \(W^2\)
\(\nabla_{W^2} \mathcal{L(g^{(i)},y^{(i)})}\)
x
\(\dots\)
y
f^1
\begin{aligned}
& W^1 \\
\end{aligned}
\begin{aligned}
& W^2 \\
\end{aligned}
\begin{aligned}
& W^L \\
\end{aligned}
f^2
f^L
\mathcal{L}(g,y)
g
\(\nabla_{W^2} \mathcal{L(g,y)}\)
Backward pass:
Run SGD to update the parameters, e.g. to update \(W^2\)
Evaluate the gradient \(\nabla_{W^2} \mathcal{L(g^{(i)},y^{(i)})}\)
Update the weights \(W^2 \leftarrow W^2 - \eta \nabla_{W^2} \mathcal{L(g^{(i)},y^{(i)}})\)
x
y
f^1
\begin{aligned}
& W^1 \\
\end{aligned}
\begin{aligned}
& W^2 \\
\end{aligned}
\mathcal{L}(g,y)
g
How do we get these gradient though?
\(\nabla_{W^1} \mathcal{L(g,y)}\)
Backward pass:
Run SGD to update the parameters, e.g. to update \(W^1\)
Evaluate the gradient \(\nabla_{W^1} \mathcal{L(g^{(i)},y^{(i)})}\)
Update the weights \(W^1 \leftarrow W^1 - \eta \nabla_{W^1} \mathcal{L(g^{(i)},y^{(i)}})\)
\(\dots\)
\begin{aligned}
& W^L \\
\end{aligned}
f^2
f^L
Outline
- Recap, the leap from simple linear models
- (Feedforward) Neural Networks Structure
- Design choices
- Forward pass
-
Backward pass
- Back-propagation
\mathcal{L}(g, y)
\mathcal{L}(g, y)
\underbrace{\quad \quad \quad } \\ n
\mathcal{L}(g, y)
\dots
x_1
x_2
x_d
x^{(i)} \quad = \left[ \begin{array}{c}
\\
\\
\\
\\
\\
\\
\\
\end{array} \right]
e.g. backward-pass of a linear regressor
\dots
y^{(i)}
\dots
\dots
- Randomly pick a data point \((x^{(i)}, y^{(i)})\)
- Evaluate the gradient \(\nabla_{w} \mathcal{L(g^{(i)},y^{(i)})}\)
- Update the weights \(w \leftarrow w - \eta \nabla_w \mathcal{L(g^{(i)},y^{(i)}})\)
w
\left[ \begin{array}{c}
\\
\\
\\
\\
\\
\\
\\
\end{array} \right]
= w^Tx
\Sigma
w_1
w_2
\dots
w_d
w_1
w_2
\dots
w_d
=
\nabla_{w} \mathcal{L(g^{(i)},y^{(i)})}
g
\mathcal{L}(g, y)
\dots
x_1
x_2
x_d
x \quad = \left[ \begin{array}{c}
\\
\\
\\
\\
\\
\\
\\
\end{array} \right]
e.g. backward-pass of a linear regressor
y
\left[ \begin{array}{c}
\\
\\
\\
\\
\\
\\
\\
\end{array} \right]
\Sigma
w_1
w_2
\dots
w_d
y \in \mathbb{R}
x \in \mathbb{R^d}
w \in \mathbb{R^d}
= \frac{\partial \mathcal{L}(g,y)}{\partial w}
\nabla_{w} \mathcal{L(g,y)}
= x \cdot 2(g - y)
\frac{\partial g}{\partial w}
= \frac{\partial[(g - y)^2] }{\partial w}
= \frac{\partial[(w^T x - y)^2] }{\partial w}
\nabla_{w} \mathcal{L(g,y)}
\frac{\partial \mathcal{L}}{\partial g}
w
=
\nabla_{w} \mathcal{L(g,y)}
= w^Tx
g
\text{ReLU}
\mathcal{L}(g, y)
\dots
x_1
x_2
x_d
x \quad = \left[ \begin{array}{c}
\\
\\
\\
\\
\\
\\
\\
\end{array} \right]
e.g. backward-pass of a non-linear regressor
y
\left[ \begin{array}{c}
\\
\\
\\
\\
\\
\\
\\
\end{array} \right]
= w^Tx
\Sigma
z
w_1
w_2
\dots
w_d
y \in \mathbb{R}
x \in \mathbb{R^d}
w \in \mathbb{R^d}
= \frac{\partial \mathcal{L}(g,y)}{\partial w}
\nabla_{w} \mathcal{L(g,y)}
= x \cdot \frac{\partial[(\text{ReLU}(z))] }{\partial z} \cdot 2(g - y)
\frac{\partial g}{\partial z}
\frac{\partial z}{\partial w}
= \frac{\partial[(g - y)^2] }{\partial w}
\nabla_{w} \mathcal{L(g,y)}
\frac{\partial \mathcal{L}}{\partial g}
w
=
\nabla_{w} \mathcal{L(g,y)}
g
= \text{ReLU}(z)
x
\(\dots\)
y
f^1
\begin{aligned}
& W^1 \\
\end{aligned}
\begin{aligned}
& W^2 \\
\end{aligned}
\begin{aligned}
& W^L \\
\end{aligned}
f^2
f^L
\mathcal{L}(g,y)
g
\underbrace{\hspace{4.7cm}}
Now, back propagation: reuse of computation
Z^L
A^2
Z^2
A^1
Z^1
\frac{\partial \mathcal{L}(g,y)}{\partial W^2}
\frac{\partial \mathcal{L}(g,y)}{\partial g}
\frac{\partial g}{\partial Z^{L}}
\frac{\partial Z^3}{\partial A^{2}}\frac{\partial A^4}{\partial Z^{3}} \dots \frac{\partial Z^L}{\partial A^{L-1}}
\frac{\partial A^2}{\partial Z^{2}}
\frac{\partial Z^2}{\partial W^{2}}
\frac{\partial \mathcal{L}(g,y)}{\partial Z^2}
\underbrace{\hspace{4cm}}
\frac{\partial \mathcal{L}(g,y)}{\partial W^2}
how to find
?
\frac{\partial \mathcal{L}(g,y)}{\partial W^1}
x
\(\dots\)
y
f^1
\begin{aligned}
& W^1 \\
\end{aligned}
\begin{aligned}
& W^2 \\
\end{aligned}
\begin{aligned}
& W^L \\
\end{aligned}
f^2
f^L
\mathcal{L}(g,y)
g
Z^L
A^2
Z^2
A^1
Z^1
\frac{\partial \mathcal{L}(g,y)}{\partial g}
\frac{\partial g}{\partial Z^{L}}
\frac{\partial Z^3}{\partial A^{2}}\frac{\partial A^4}{\partial Z^{3}} \dots \frac{\partial Z^L}{\partial A^{L-1}}
\frac{\partial A^2}{\partial Z^{2}}
\frac{\partial \mathcal{L}(g,y)}{\partial Z^2}
\underbrace{\hspace{4cm}}
back propagation: reuse of computation
\frac{\partial Z^2}{\partial W^{2}}
\underbrace{\hspace{4.7cm}}
\frac{\partial \mathcal{L}(g,y)}{\partial W^2}
how to find
?
\underbrace{\hspace{6.5cm}}
\frac{\partial \mathcal{L}(g,y)}{\partial W^1}
\frac{\partial Z^2}{\partial A^{1}}
\frac{\partial A^1}{\partial Z^{1}}
\frac{\partial Z^1}{\partial W^{1}}
x
\(\dots\)
y
f^1
\begin{aligned}
& W^1 \\
\end{aligned}
\begin{aligned}
& W^2 \\
\end{aligned}
\begin{aligned}
& W^L \\
\end{aligned}
f^2
f^L
\mathcal{L}(g,y)
g
Z^L
A^2
Z^2
A^1
Z^1
\frac{\partial \mathcal{L}(g,y)}{\partial g}
\frac{\partial g}{\partial Z^{L}}
\frac{\partial Z^3}{\partial A^{2}}\frac{\partial A^4}{\partial Z^{3}} \dots \frac{\partial Z^L}{\partial A^{L-1}}
\frac{\partial A^2}{\partial Z^{2}}
\frac{\partial \mathcal{L}(g,y)}{\partial Z^2}
\underbrace{\hspace{4cm}}
back propagation: reuse of computation
how to find
\frac{\partial \mathcal{L}(g,y)}{\partial W^1}
?
Summary
- We saw that introducing non-linear transformations of the inputs can substantially increase the power of linear tools. But it’s kind of difficult/tedious to select a good transformation by hand.
- Multi-layer neural networks are a way to automatically find good transformations for us!
- Standard NNs have layers that alternate between parametrized linear transformations and fixed non-linear transforms (but many other designs are possible.)
- Typical non-linearities include sigmoid, tanh, relu, but mostly people use relu.
- Typical output transformations for classification are as we've seen: sigmoid, or softmax.
- There’s a systematic way to compute gradients via back-propagation, in order to update parameters.
Thanks!
We'd love to hear your thoughts.
6.390 IntroML (Fall24) - Lecture 6 Neural Networks
By Shen Shen
