Introduction to Algorithm
Updates
- 2019 - Spring , Set C++14 as Default Version

What is ALGORITHM?
演算法是什麼?
- 計算的方法?
- 思考的方法?
- 數學公式?
- 電腦程式?
[al-guh-rith-uh m]

What is ALGORITHM?
- 精確定義演算法是困難的,但他有一些重要特徵
- 0個以上的輸入
- 1個以上的輸出
- 有限多的步驟數可執行完畢
- 每一個步驟都是精確無歧異的
計算理論
- 採用什麼計算模型 Formal Lanauage
- 自動機的設計
- 哪些是能計算的、哪些是不能計算的Computability Theory
- 自動機的能力
- 要用多少時間、要用多少儲存Complexity Theory
- 自動機的效率
Why IOI or ACM contest ?
- 演算法競賽
- IOI, ACM-ICPC
- EDA
- 資安競賽
- CTF
不同型式的資訊競賽
- 黑客松
- Hackathon Taiwan
- 軟體開發
- 很多奇怪的比賽
Keep thinking
(只要夠大牌,用法就是對的)

Time Complexity
好的演算法?
- 想法很簡單?
- 實作很簡單?
- 廢話比較少?
- 需要的計算量很少?
時間複雜度
- 用來描述一個演算法需要用多少計算時間來解決問題
- 找\(N\)個元素最大值
- 需要至少把每一個元素都檢查一次
- 找\(N\)個元素最大值
int mx = a[0];
for(int i=1;i<N;++i)
{
mx = max( mx , a[i] );
}Big-O 表示法
- 計算機科學中,使用符號\(O\)表示一個函數的成長關係
如果\(f(x)\in \mathcal{O}(g(x))\)
就存在\(c\)與\(x_0\)
如果\(x>x_0\)
\(c\times g(x)\geq f(x)\)
Big-O 表示法
如果\(f(x)\in \mathcal{O}(g(x))\)

Big-O 表示法
如果\(f(x)\in \mathcal{O}(g(x))\)
就存在\(c\)與\(x_0\)

\(x_0\)
\(c\times\)
Big-O 表示法
如果\(f(x)\in \mathcal{O}(g(x))\)
就存在\(c\)與\(x_0\)
如果\(x>x_0\)

\(x_0\)
\(c\times\)
\(x\)
Big-O 表示法
如果\(f(x)\in \mathcal{O}(g(x))\)
就存在\(c\)與\(x_0\)
如果\(x>x_0\)
\(c\times g(x)\geq f(x)\)

\(x_0\)
\(c\times\)
\(x\)
\(c\times g(x)\)
\(f(x)\)
Example
- 證明\(x^2-x+2 \in O(x^2)\)
Example
- 證明\(x^2-x+2 \in O(x^2)\)
如果\(x\geq1\)
\(x^2-x+2\)
\(\leq x^2+x+2\)
\(\leq x^2+x^2+2x^2=4x^2\)
Example
- 證明\(x^2-x+2 \in O(x^2)\)
如果\(x\geq1\)
\(x^2-x+2\)
\(\leq x^2+x+2\)
\(\leq x^2+x^2+2x^2=4x^2\)
設\(c=4,x_0=1\)
如果\(x_0\leq x\)
\(x^2-x+2\leq cx^2\)
因此
\(x^2-x+2 \in O(x^2)\)
Fact
- 對於多項式\(f(x)=a_0+a_1x+a_2x^2+\cdots +a_nx^n\)
\(f(x)\in \mathcal{O}(x^n)\)
- 多項式的複雜度就是\(x\)次數最大的項
- 當\(x\)很大的時候,其他的數字比例小的可以忽略
演算法與Big-Oh
- 計算演算法對於任意資料,要花費幾個基本運算算完
- 基本運算ex:
- 基本型態的加減乘除(3+5)
- 存取一個基本型態的資料
- 寫入一個基本型態的資料
- 基本運算ex:
- 計較細節的操作過於瑣碎,因此使用bigO來表達
Example
- 計算下演算法的BigO複雜度
// Find max value index in array
int index = -1;
for(int i=0;i<N;++i)
{
bool flag = true;
for(int j=0;j<N;++j)
{
if( a[j] > a[i] )
flag = false;
}
if( flag )
index = i;
}如果一個演算法複雜度是\(O(x^2)\),表示該方法最糟不會比所有\(O(x^2)\)的方法糟糕
Example
- 計算下演算法的BigO複雜度
// Find max value index in array
int index = 0;
for(int i=1;i<N;++i)
{
if( a[i] > a[index] )
index = i;
}Order of the Function
- 由BigOh我們可以發現函數的成長幅度有階級關係
- 如果\(f(x)\)是\(O(x)\),那它也是\(O(x^2)\)
- 如果一個函數的階級越大,數值成長速度越快
\(O(x^5)\)
\(O(x^3)\)
\(O(x)\)
Order of the function

Quick fact
- 複雜度由小到大排列
- \(O(1)\) 用公式解解一元二次方程式
- \(O(\alpha (n) )\) Disjoint Set
- \(O(\log n)\) 二分搜尋法
- \(O(\sqrt{n})\)
- \(O(n)\) 找最大值
- \(O(n\log n)\) C++的排序
- \(O(n^2)\) 泡沫排序法
\(O(\log n!)=O(n\log n)\)
Quick fact
- 複雜度由小到大排列
- \(O(n\log n)\) C++的排序
- \(O(n^2)\) 泡沫排序法
- \(O(n^3)\) 普通矩陣乘法
- \(O(e^{\left(c + o(1)\right)(\ln n)^{\alpha}(\ln \ln n)^{1-\alpha}})\) 我覺得這很酷
- \(O(2^n)\) 旅行推銷員問題DP
- \(O(n!)\) 枚舉排列組合
競賽的經驗法則
- 假設對於一個題目想到了複雜度是\(O(N^2)\)的方法
- 這個方法會不會TLE呢?
把題目測資上限\((N=20000)\)代入
如果大於\(10^8\),基本上就會TLE
More topics
- 平攤複雜度
- 遞迴複雜度與主定理
- 什麼是P,什麼是NP?
Package data
打包資料
- 有的時候會想要把有關聯的資料(ex 座標)合併在一起,同步操作,在C++有許多種方法可以使用
| 資料數量 | |
|---|---|
| struct/class | 任意多 |
| std::pair | 2 |
| std::tuple | 任意多 |
struct
- 在C++中,struct與class功能一樣,除了預設物件屬性不同,一般而言比賽都用struct。
//定義
struct Point{
int x;
int y;
string name;
};
//宣告
Point data, array[666];
//使用變數
data.x = data.y = array[2].x = 7122;
data.name = "StarStar";建構子
- 在變數被宣告時,呼叫用來初始化的函數
struct Point{
int x;
int y;
string name;
Point(){ //建構子
name = "7122";
}
};
//宣告
Point data; //會呼叫建構子
cout<< data.name ;
Output:
7122有參數的建構子
- 在變數被宣告時,呼叫用來初始化的函數
struct Point{
int x;
int y;
string name;
Point(int a,int b){ //建構子
x=a; y=b;
}
};
//宣告
Point data(94,87); //會呼叫建構子
cout<< data.x << ' ' <<data.y ;
Output:
94 87有參數的建構子
- 存在自定義建構子時,不會生成預設(無參數)建構子
struct Point{
int x;
int y;
string name;
Point(int a,int b){ //建構子
x=a; y=b;
}
};
//宣告
Point data; //會呼叫建構子
Output:
Compile Error!
Can not find Point()有參數的建構子
- 存在自定義建構子時,不會生成預設(無參數)建構子
struct Point{
int x;
int y;
string name;
Point(int a,int b){ //建構子
x=a; y=b;
}
Point(){ //建構子 called
name="MAAAA";
}
};
//宣告
Point data;
cout<<data.name;
Output:
MAAAAstd::pair
- 把兩個型態綁一起
#include<utility> //also in algorithm
using pis = std::pair<int,string>;
typedef std::pair<int,string> pis2; //Old C++
pii data;
data.first = 7122;
data.second = "TFcis";
data = {123,"ABC"};
data = make_pair(123,"ABC");std::pair
- std::pair支援比較運算,皆以字典序比較
using pii = pair<int,int>;
pii a[3] = { {2,1},{1,2},{3,0} };
sort( a,a+3 );
for( auto v:a )
cout<<v.first<<' '<<v.second<<endl;Output:
1 2
2 1
3 0std::pair
- 兩個不夠用,可以自己套自己 = =
typedef pair<int,pair<int,int>> piii; //C++11
typedef pair<int,pair<int,int> > piii2;
piii a;
a.first = a.second.first = a.second.second = 87std::tuple
- 把任意多的資料綁一起
#include<utility> //also in algorithm
using tiii= std::tuple<int,int,int>;
tiii a;
a = {1,2,3}; // C++11 and g++ >= 6
a = make_tuple(1,2,3); // Always OK
std::tuple (c++11)
- tuple拆解資料
#include<utility> //also in algorithm
using tiii= std::tuple<int,int,int>;
tiii a = {1,2,3};
auto [i,j,k] = a; //C++17
int i,j,k;
tie(i,j,k) = a; //Always OK
i = get<0>(a);
j = get<1>(a);
k = get<2>(a); //Always OK
Basic Data Structure
with STL
What is STL
- C++ Standard Template Library
- 由標準實作的演算法與資料結構
- 目前最新規格書N4700有1416頁
- 多用多查資料
- cppreference(白)
- cplusplus(藍)
C++ 標準
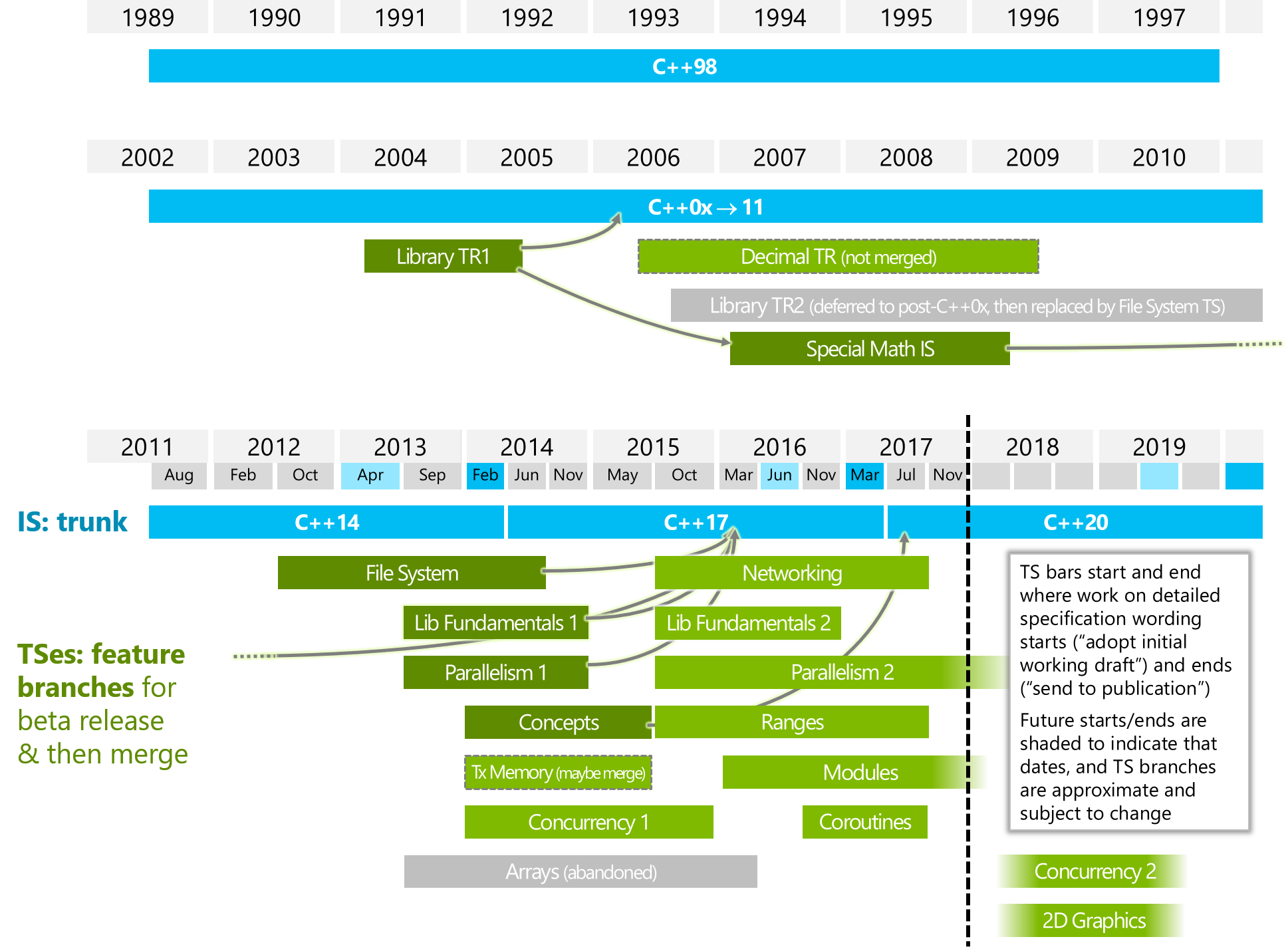
- 目前的最新C++標準是C++17
- 大多數比賽使用C++/14
- 從2017年開始ACM-ICPC使用C++14為競賽標準
- 大陸OJ通常連C++11都沒有
C++ ISO Status
vector
- 中文翻譯為「向量」,不過沒人用
- 強化版的陣列,大小可以自動變大
- 在尾部的元素操作效率佳
#include<vector>
std::vector<int> arr;
arr.resize(N); //設定大小為N
arr[0] = arr[N-1] = 1; //與一般陣列一樣vector 新增元素
- 使用emplace_back在最後方新增元素
- 複雜度為平攤\(O(1)\)
vector<int> v;
v.emplace_back(2);
for(int i:v) cout<<i<<' ';Output:
1 2vector 新增元素 - 2
vector<tuple<int,int,int>> v;
v.emplace_back(7,8,9);
v.push_back({1,2,3});//C++11 & G++ >= 6.0
v.push_back(make_tuple(4,5,6));
for(auto [i,j,k]:v) //C++17
cout<<i<<' '<<j<<' '<<k<<endl;Output:
1 2 3
4 5 6
7 8 9
I2A
By sylveon
I2A
Intro to algorithm
- 1,588



