Robustifying Smoothened Dynamics
Policy Search through Contact Dynamics
\begin{aligned}
F(\alpha;{\color{red}x_i},{\color{green}p})\quad & \coloneqq \left[\sum^\infty_{t=0} \gamma^t r(x_{t},u_{t})\right] \\
\text{s.t.}\quad & x_{t+1}=f(x_t,u_t,{\color{green} p}),\;\\
& u_t = \pi(x_t,\alpha), \quad x_0 = {\color{red} x_i}
\end{aligned}
Original problem formulation:
Find a deterministic policy that minimizes sum of rewards.
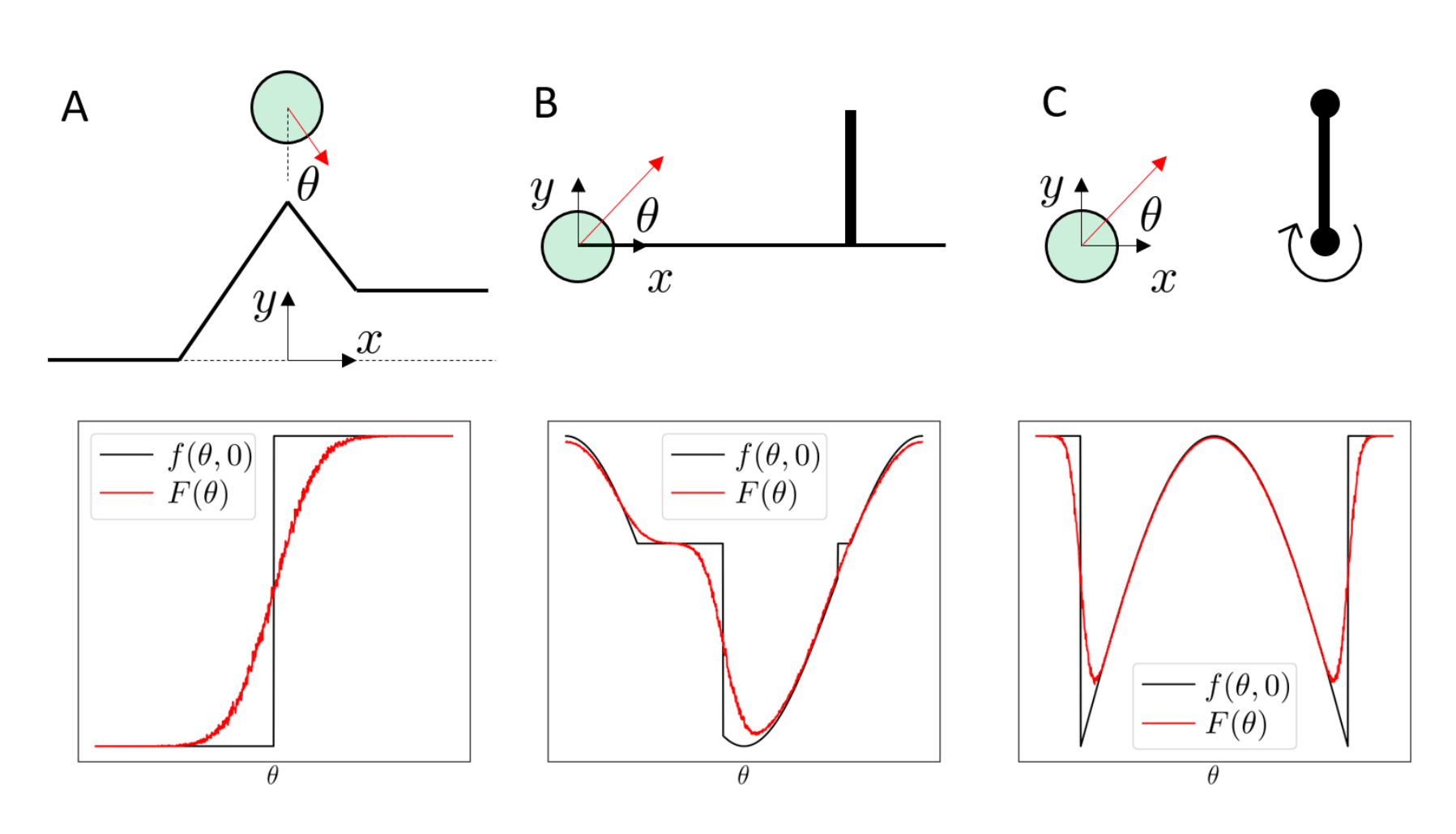
1. Flatness
2. Stiffness
Challenges of Gradient-based Optimization
\begin{aligned}
\min_\alpha F(\alpha;{\color{red}x_i},{\color{green}p})
\end{aligned}
Policy Search through Contact Dynamics
\begin{aligned}
F(\alpha;{\color{red} x_i}, {\color{green} p}, {\color{blue} w_t})\quad & \coloneqq \left[\sum^\infty_{t=0} \gamma^t r(x_{t},u_{t})\right] \\
\text{s.t.}\quad & x_{t+1}=f(x_t,u_t,{\color{green}p}),\;\\
& u_t = \pi(x_t,\alpha) + {\color{blue} w_t},\quad x_0={\color{red} x_i}
\end{aligned}
Perhaps unknowingly, many RL formulations benefit from specifying a more relaxed objective with a stochastic formulation.
Randomization of initial conditions
Randomization of domain parameters
Randomization of stochastic policy
\begin{aligned}
\min_\alpha {\color{red}\mathbb{E}_{x_i}}{\color{green}\mathbb{E}_{p}}{\color{blue}\mathbb{E}_{w_{0:\infty}}}\left[F(\alpha;{\color{red} x_i},{\color{green} p},{\color{blue} w_{0:\infty}})\right]
\end{aligned}
Policy Search through Contact Dynamics
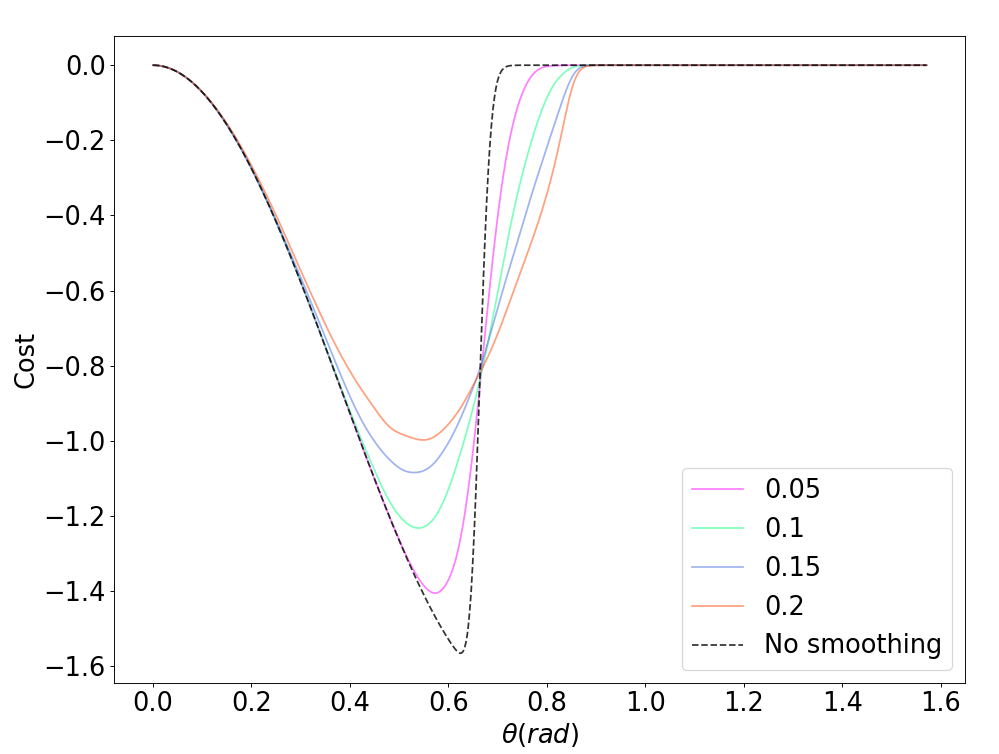
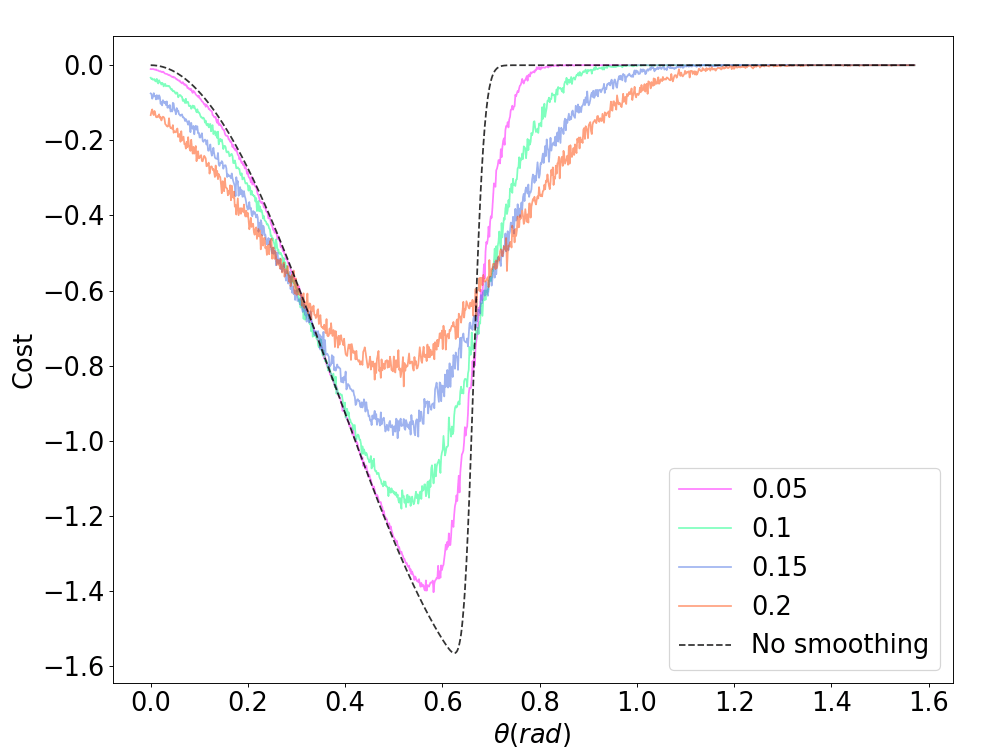
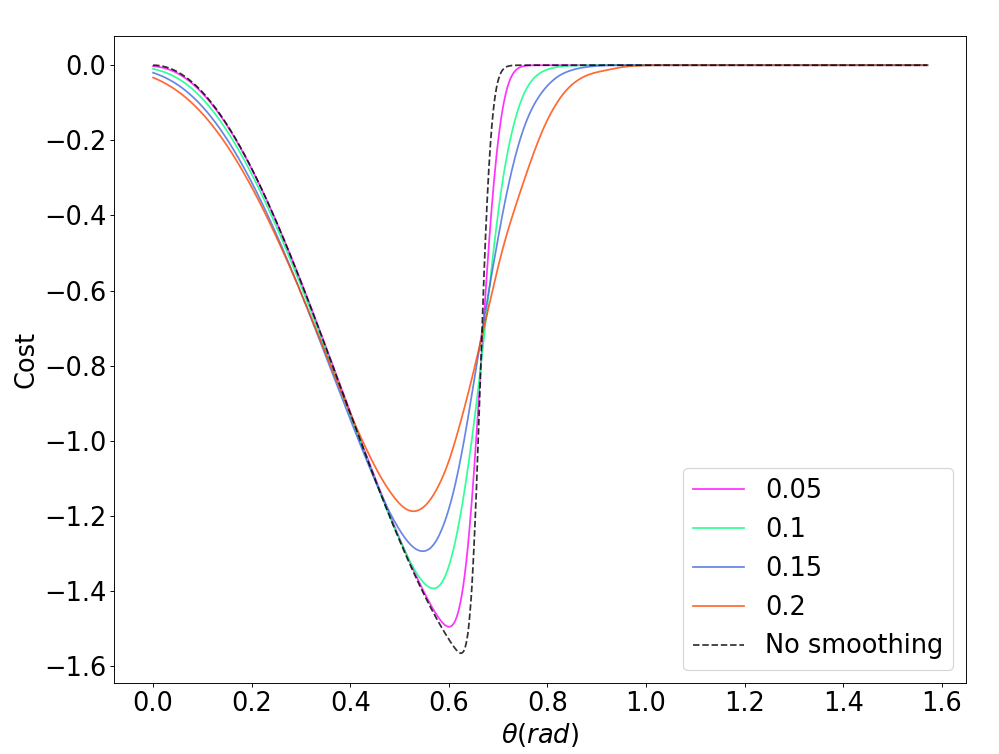
Policy Randomization
Domain Randomization
Initial Condition Randomization
Randomization potentially alleviates flatness and stiffness
Policy Search through Contact Dynamics
Policy Randomization
Domain Randomization
Initial Condition Randomization
Randomized smoothing also encodes robustness
Rate of Bias
Suboptimality
\begin{aligned}
e_\rho \coloneqq V(\alpha^*_\rho) - V(\alpha^*)
\end{aligned}
Suboptimality gap (Bias)
Suboptimality Stiffness
\begin{aligned}
\Delta e_\rho \coloneqq \frac{V(\alpha^*_\rho) - V(\alpha^*)}{\rho}
\end{aligned}
\begin{aligned}
(\varepsilon,\delta) \coloneqq \inf_{\|\Delta p\|\leq \varepsilon} V(\alpha^*,\hat{p} + \Delta p)-V(\alpha^*,\hat{p}) \leq \delta
\end{aligned}
Robustness
Suboptimality
\begin{aligned}
\alpha^* & = \text{argmin}_\alpha V(\alpha)\\
\alpha^*_\rho & = \text{argmin}_\alpha \bar{V}_\rho(\alpha)
\end{aligned}
Pitfalls of Randomized Smoothing
Challenge 1. Sample-Inefficient Exploration
Getting out of flatness requires lots of samples.
Need to have lot of samples to eventually reach a non-flat region.
Pitfalls of Randomized Smoothing
Challenge 2. Empirical Bias from Stiff Underlying Landscape
Example: Domain Randomization
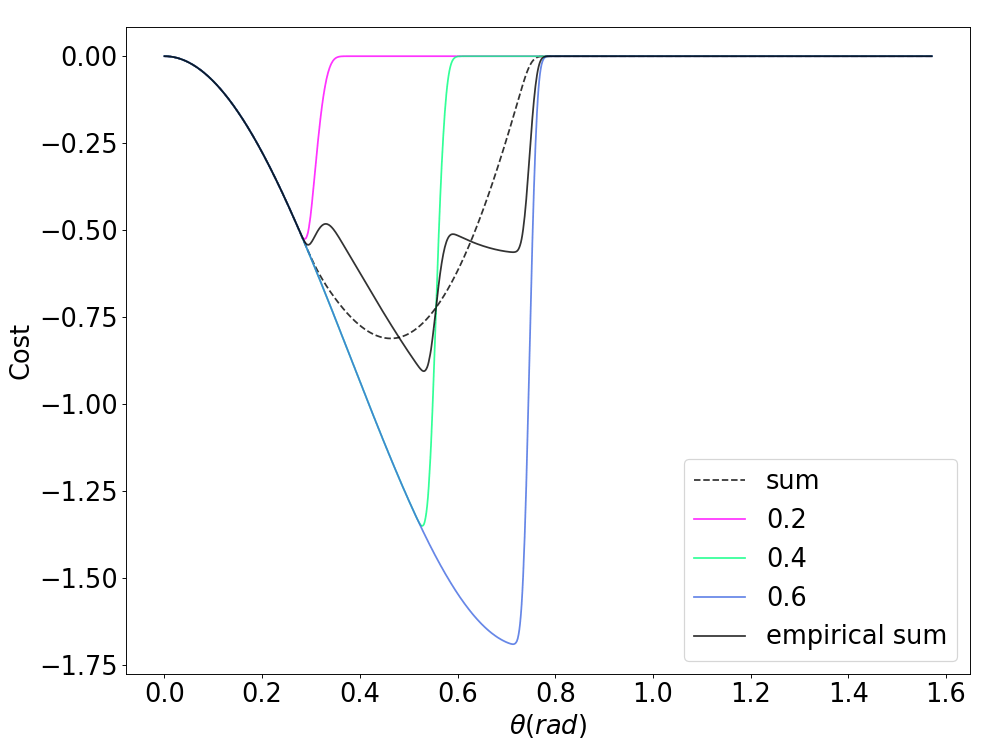
Summing up gradients does not result in direction of true gradient!
\begin{aligned}
\mathbb{E}_p V(\alpha, p)
\end{aligned}
\begin{aligned}
\frac{1}{N}\sum_i V(\alpha,p_i)
\end{aligned}
What causes stiffness?
x_3(\alpha_1)
x_2(\alpha_1)
x_1(\alpha_1)
x_1(\alpha_2)
x_2(\alpha_2)
x_3(\alpha_2)
\lim_{\alpha_2\rightarrow\alpha_1}\frac{r_3(\alpha_2) - r_3(\alpha_1)}{x_3(\alpha_2) - x_3(\alpha_1)}\cdot \frac{x_3(\alpha_2) - x_3(\alpha_1)}{x_2(\alpha_2) - x_2(\alpha_1)}\cdot {\color{red} \frac{x_2(\alpha_2) - x_2(\alpha_1)}{x_1(\alpha_2) - x_1(\alpha_1)}}\cdot \frac{x_1(\alpha_2) - x_1(\alpha_1)}{x_0(\alpha_2) - x_0(\alpha_1)}\cdot\frac{x_0(\alpha_2) - x_0(\alpha_1)}{\alpha_2 - \alpha_1}
x_0(\alpha_1)
x_0(\alpha_2)
\frac{\partial r_3}{\partial \alpha} = \frac{\partial r_3}{\partial x_3}\frac{\partial x_3}{\partial x_2}{\color{red}\frac{\partial x_2}{\partial x_1}}\frac{\partial x_1}{\partial x_0}\frac{\partial x_0}{\partial \alpha}
Started off close, ended up far!
Rewards are tied to states and trajectories.
Stiff dynamics causes vastly different trajectories in state. If these are different in the direction of the reward, they directly translate to stiff value landscapes.
Dynamic smoothing alleviates stiffness / flatness
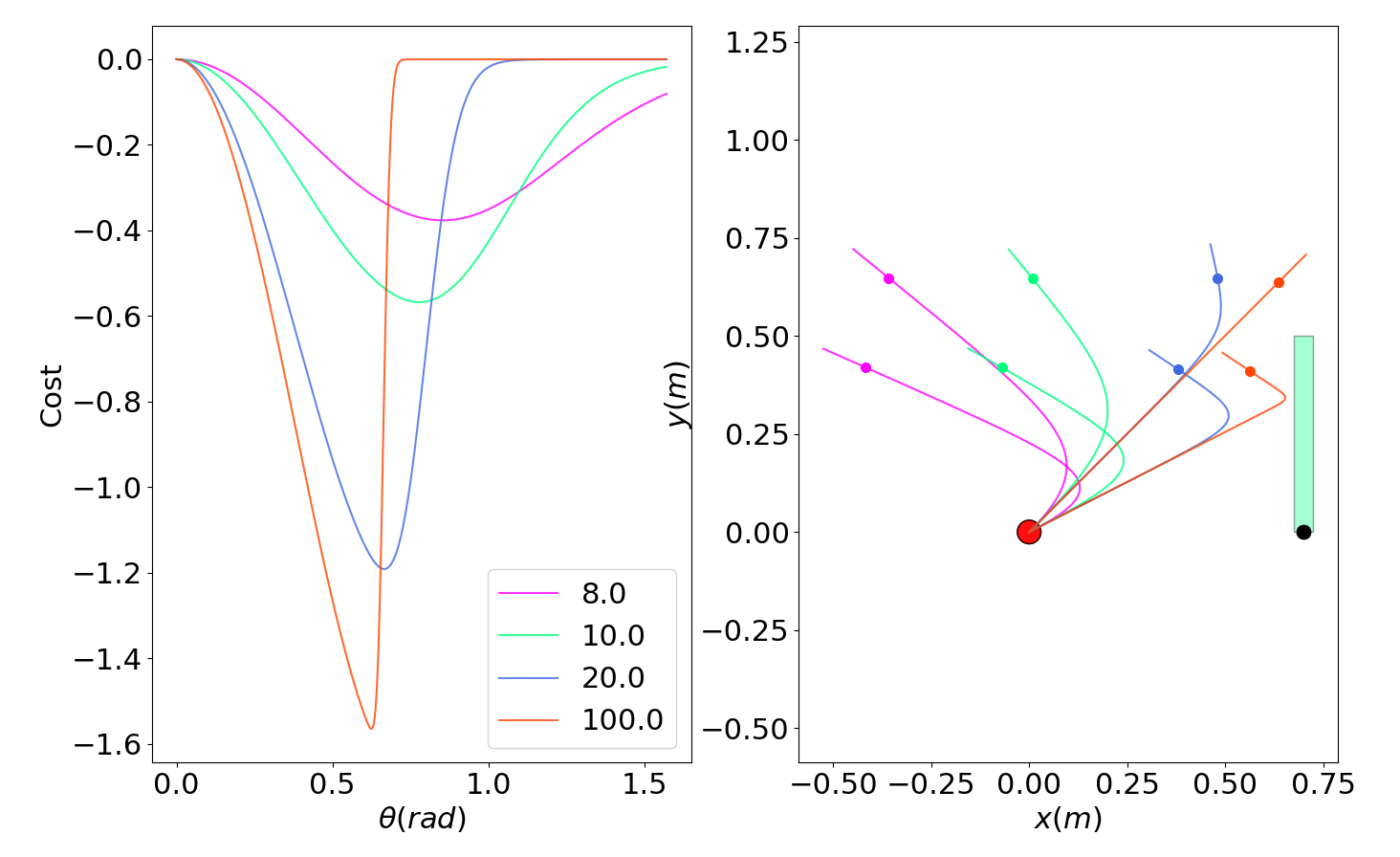
Dynamic smoothing alleviates flatness and stiffness without MC.
Harmful bias of dynamic smoothing
However, dynamic smoothing can develop harmful bias.
What kind of cases cause smoothing to be badly biased?
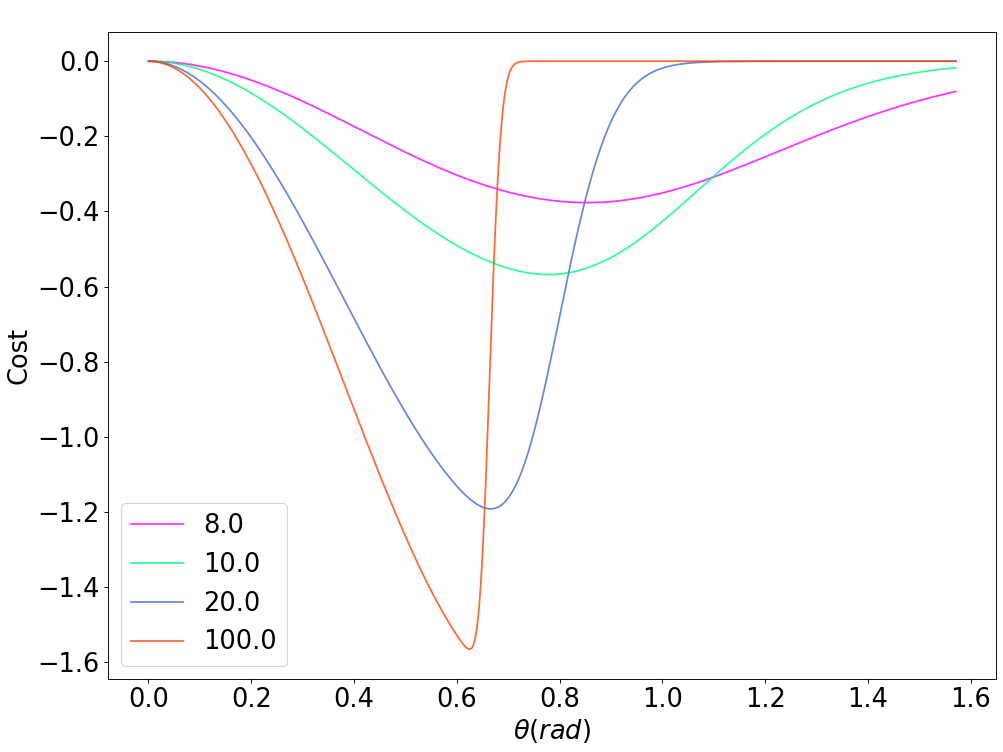
Dynamic Smoothing
Randomized Value Smoothing
RS solutions become suboptimal gracefully.
Dynamic smoothing solutions fail catastrophically.
Dynamic Smoothing alleviates Flatness
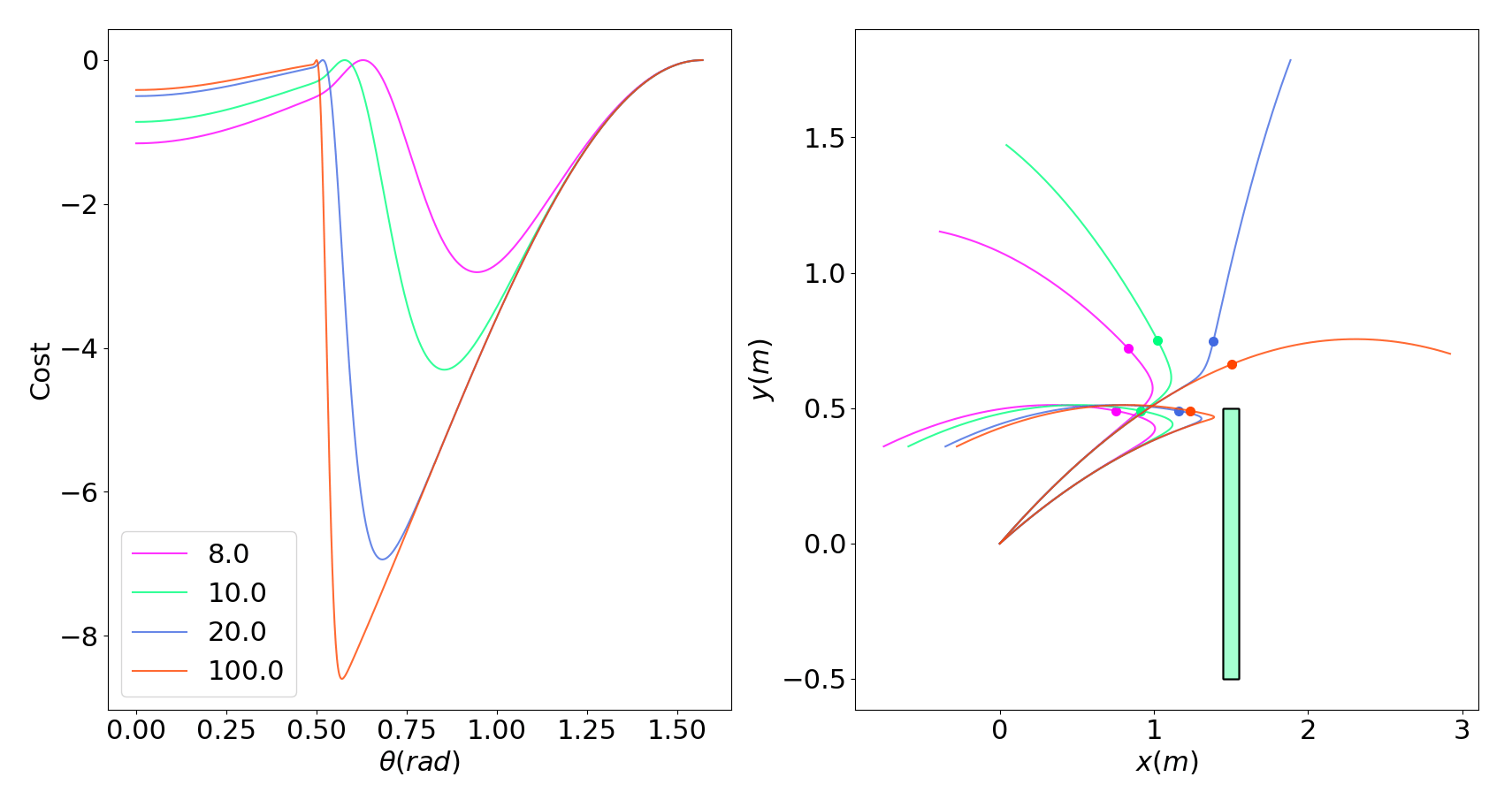
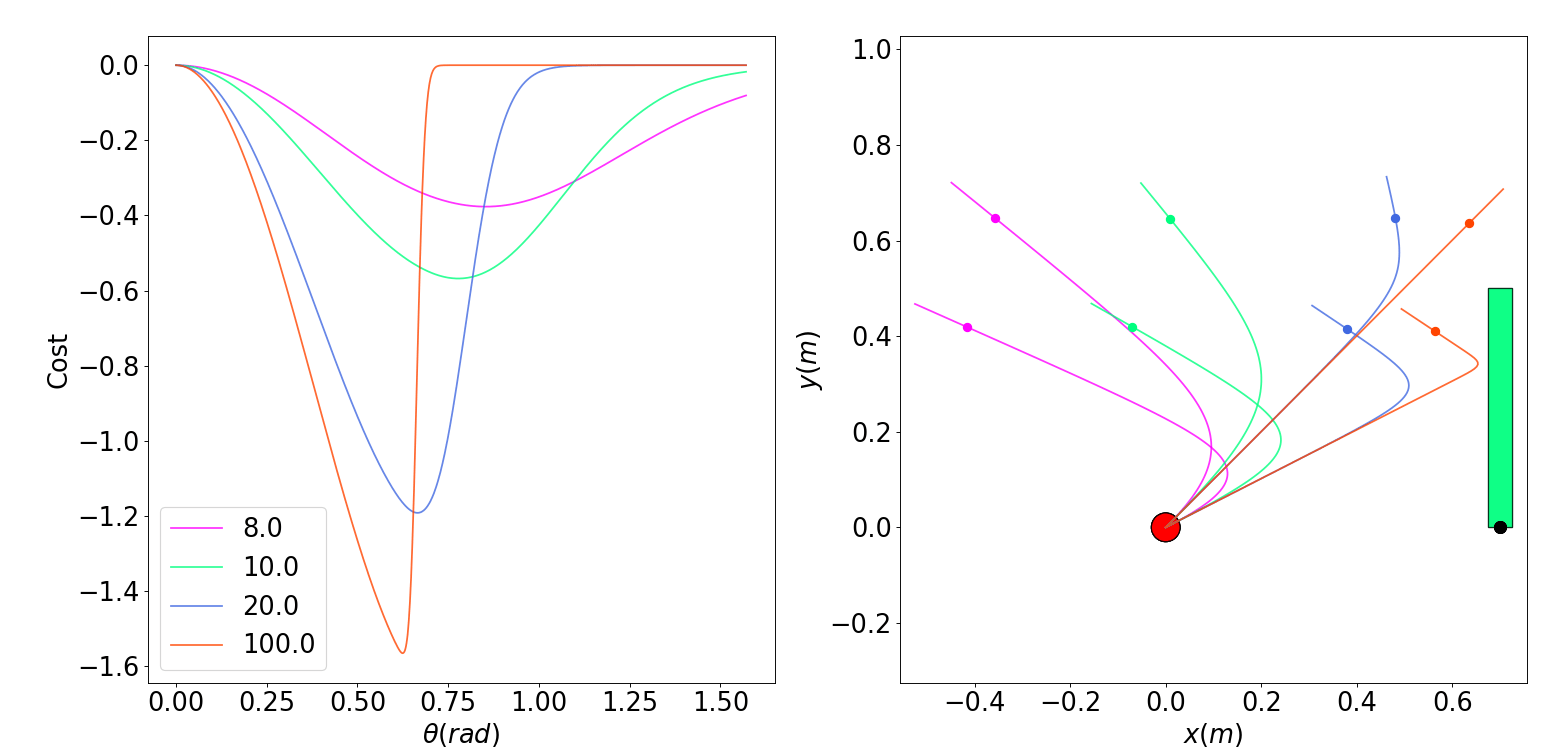
Contact-Averse Tasks
Contact-Seeking Tasks
Dynamic smoothing has "beneficial" bias since the smooth solution assumes force-from-a-distance.
Dynamic smoothing has "catastrophic" bias since force-from-a-distance does not result in contact.
A Combined Solution
Randomized Value Smoothing
Dynamic Smoothing
Solutions are more robust, often develop "beneficial" bias.
Sample-inefficient in exploration
Suffers from empirical bias when underlying landscape is stiff.
Sample-efficient method for smoothing
Develops bad bias in contact-seeking, finds non-robust solutions.
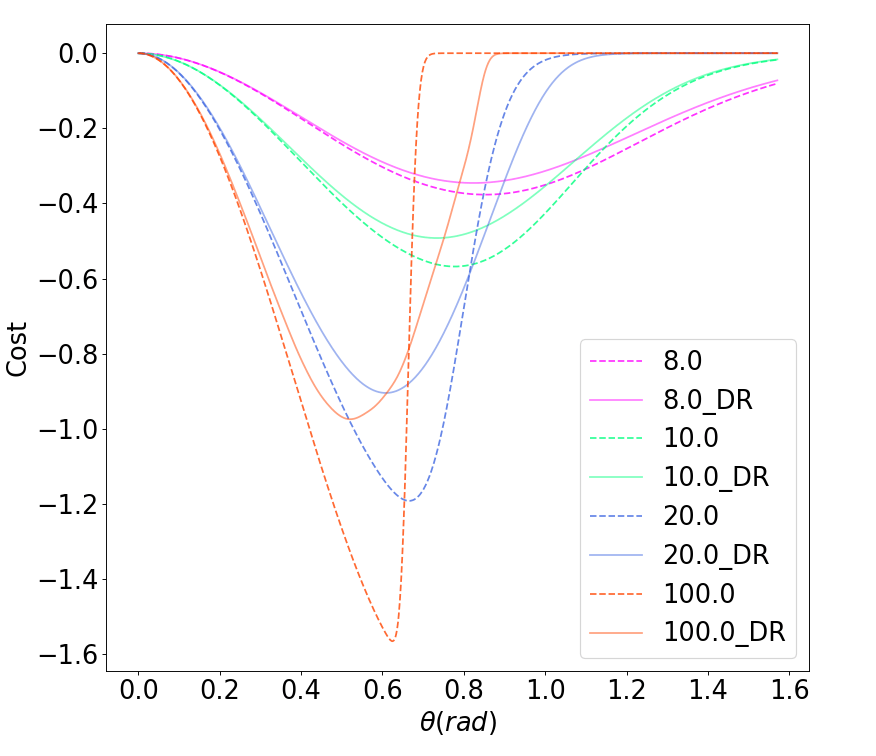
Domain Randomization w/ Dynamic Smoothing
Stochastic smoothing schemes suffer less from empirical bias due to underlying smooth dynamics.
Can strategically design domain randomization distribution to be robust to dynamic smoothing bias.
Domain Randomization w/ Dynamic Smoothing
DR says we don't need to be terribly accurate with dynamics as long as we can randomize.
So why not choose an inaccurate but smooth contact model to leverage this?
Copy of DiffRL
By Terry Suh
