Cursus et recherche effectuée
18 - 04 - 2024
Thomas Borsoni
Laboratoire Jacques-Louis Lions, Sorbonne Université
Entretien postdoc CERMICS
2015/16
L3 Mathématiques
Recrutement
à l'ENS Cachan sur concours
Stage d'initiation à la recherche - 2 m
CMLA (ENS Cachan)
Stage d'initiation à la recherche - 4 m
Univ. Koblenz-Landau (All.)
Stage de recherche - 4 m
CMLA (ENS Cachan)
Stage de recherche - 4 m
IRCAM (Paris)
Stage de recherche - 10 m
Univ. Parme (Italie)
Obtention du diplôme de l'ENS
2017/18
M1 Mathématiques
voie Hadamard
Césure
2018/19
M2 « Maths en Action »
Université Lyon 1
2019/20
M2 « Mathématiques de la modélisation »
Sorbonne Université
2020/21
Année « ARPE »
Cursus mathématique à
l'ENS Paris-Saclay
interpolation de spectrogrammes par transport optimal, code en Python
« Méthodes mathématiques et analyse numérique pour la simulation moléculaire » G. Stoltz
Thèse en Mathématiques
Laboratoire Jacques-Louis Lions (LJLL), Sorbonne Université
supervisée par Laurent Boudin (LJLL/SU) et Laurent Desvillettes (IMJ-PRG/UPCité)
« Contributions autour de l'équation de Boltzmann et certaines de ses variantes »
Axes de recherche
- Modélisation / physique mathématique
- Analyse fonctionnelle / EDP
- Simulations numériques
Mission d'enseignement
Responsabilités
- Représentant doc. au LJLL (élu)
- Membre du "pôle écoute"
Moniteur
Sorbonne Université
Exposés : conférences et workshops
Invité à présenter :
- 4 conférences (2 Fr)
- 6 séminaires (3 Fr)
Participant avec poster (Italie)
09/2021 - 08/2024
Recherche
Modélisation
Boltzmann polyatomique
Analyse
Boltzmann quantique
L'équation de Boltzmann et des variantes
\partial_t f \textcolor{purple}{+ v \cdot \nabla_x f} = Q(f)
f(t,x,v)
f(t,x,v,\textcolor{orange}{\zeta})
Q_{\textcolor{blue}{\varepsilon}}(f)
Q(f)
Modélisation
Boltzmann polyatomique
Recherche 1/2
1. Développement d'un modèle de Boltzmann général pour les gaz polyatomiques
- généralisation
- nouveaux modèles "ab initio"
- sens physique et calculabilité de paramètres
Communications in Mathematical Physics
Kinetic and related models
2. Etude d'une propriété de compacité, cadre polyatomique singulier ("résonant")
Journal of Mathematical Analysis and Applications
3. Développement d'un modèle quasi-résonant
- modélisation, propriétés
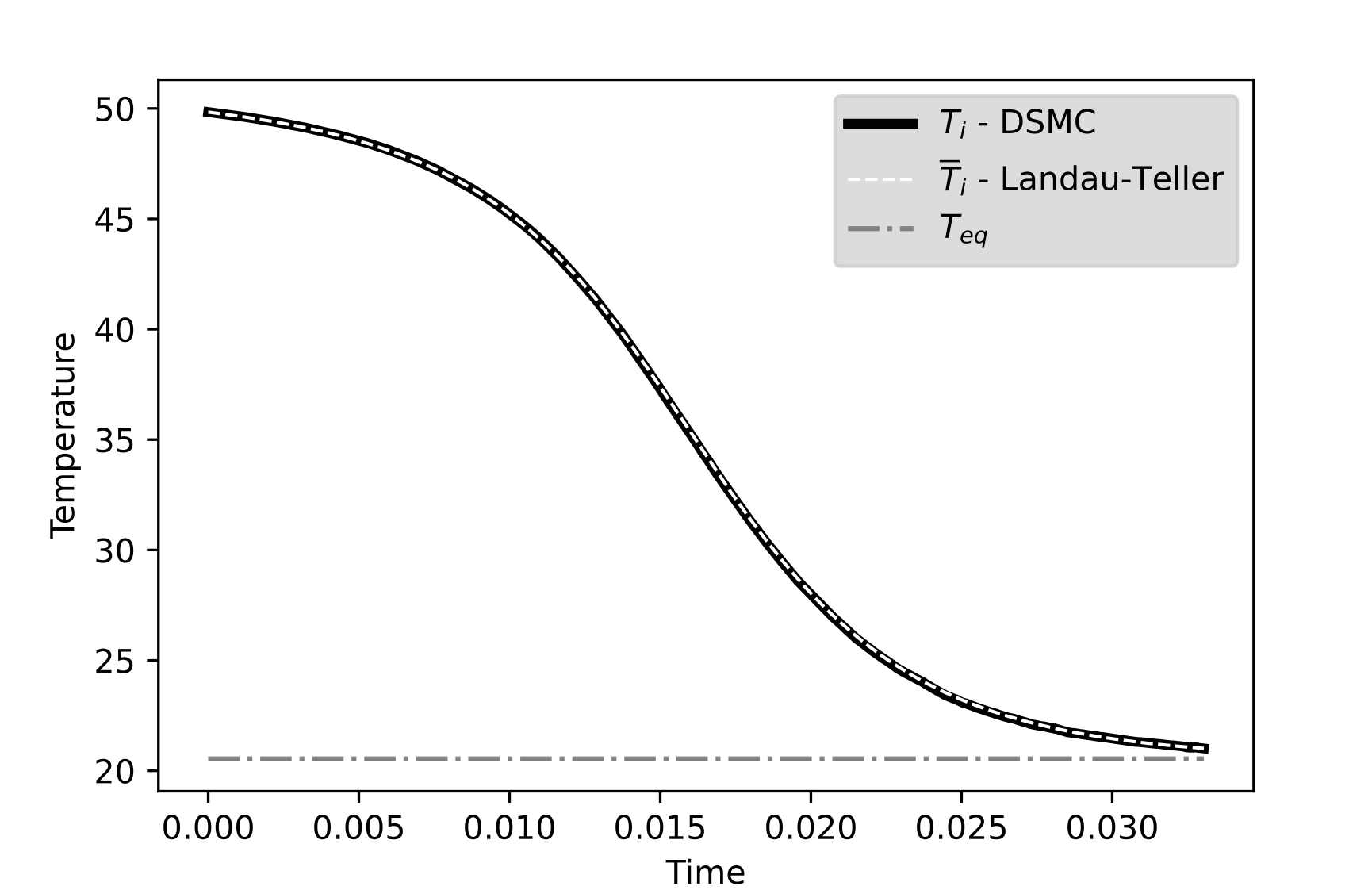
- dérivation rigoureuse d'équations connues (Landau-Teller)
- validation par expériences numériques (DSMC)
avec M. Bisi, M. Groppi
avec L. Boudin,
F. Salvarani
avec L. Boudin,
J. Mathiaud,
F. Salvarani
Expériences numériques
Boltzmann polyatomique
quasi-résonant
Développement d'un code DSMC (Direct Simulation Monte Carlo) en Python pour simuler Boltzmann homogène 3D
- Approche Monte Carlo
- Compilation Just-In-Time et parallélisation
Recherche 1'/2
Recherche 2/2
Analyse
Boltzmann quantique
Objectif : convergence des solutions de Boltzmann-Fermi-Dirac vers leur équilibre (statistique
de Fermi-Dirac) avec taux explicite
Méthode entropique :
- Inégalités fonctionnelles reliant entropie et dissipation d'entropie
- Contrôle des solutions (moments, norme \(L^\infty\), bornes inférieures)
An. fonc.
An. EDP
1. Méthode permettant le transfert de toute inégalité entropie/dissipation d'entropie de Boltzmann
classique vers Boltzmann-Fermi-Dirac
- inégalité fonctionnelle permettant le transfert
- généralisation des inégalités de Csiszar-Kullback-Pinsker
Article accepté à Journal of Statistical Physics
2. Contrôle des solutions et preuve de convergence vers l'équilibre avec taux explicite (spat. hom.)
et uniforme en le param. quantique \(\varepsilon\)
- borne \(L^\infty\), bornes inférieures
- obtention d'un taux de convergence explicite
Article soumis
avec B. Lods
Liste de publications
- T. Borsoni, M. Bisi, M. Groppi : A general framework for the kinetic modelling of polyatomic gases. Communications in Mathematical Physics, 2022, 393 (1), pp.215-266.
- T. Borsoni, L. Boudin, F. Salvarani : Compactness property of the linearized Boltzmann operator for a polyatomic gas undergoing resonant collisions. Journal of Mathematical Analysis and Application, 2023, 517 (1), p. 126579.
- M. Bisi, T. Borsoni, M. Groppi : An internal state model for chemically reacting mixtures of monatomic and polyatomic gases. Kinetic and Related Models, 2024, 17 (2), pp.276-311.
- T. Borsoni : Extending Cercignani's conjecture results from Boltzmann to Boltzmann-Fermi-Dirac equation. Accepté à Journal of Statistical Physics, 2024.
- T. Borsoni, B. Lods : Quantitative relaxation towards equilibrium for solutions to the Boltzmann-Fermi-Dirac equation with cutoff hard potentials. Soumis, preprint HAL, 2024.
Entretien CERMICS
By Thomas Borsoni
