Contributions around the Boltzmann equation and some of its variants

Thomas Borsoni

supervised by

Laurent Boudin & Laurent Desvillettes

Mesoscopic

Microscopic

Macroscopic

(statistical)

description of gases

introduction:

original Boltzmann equation

Density of molecules: \(f \equiv f_{t,x}(v)\)

The original Boltzmann equation

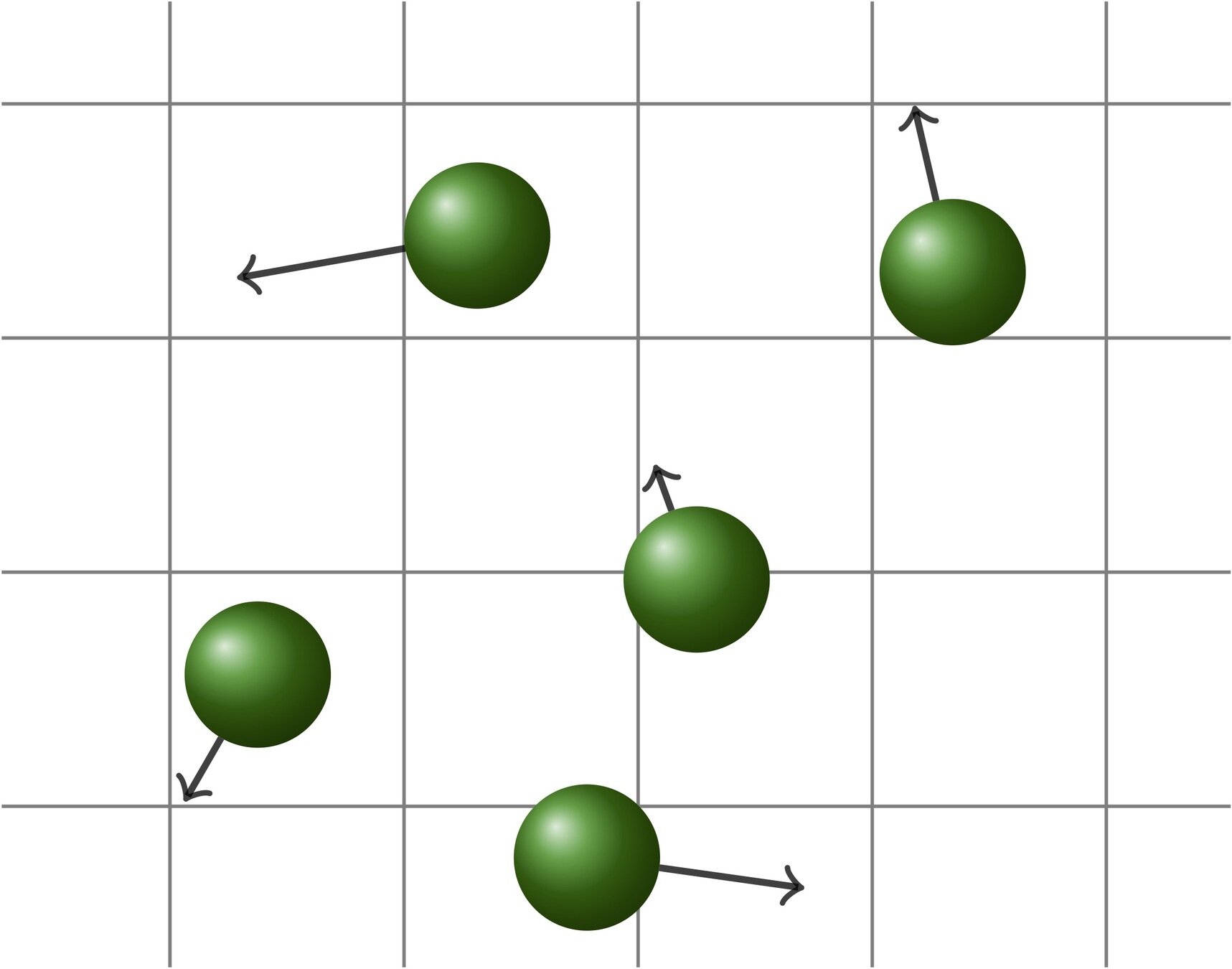
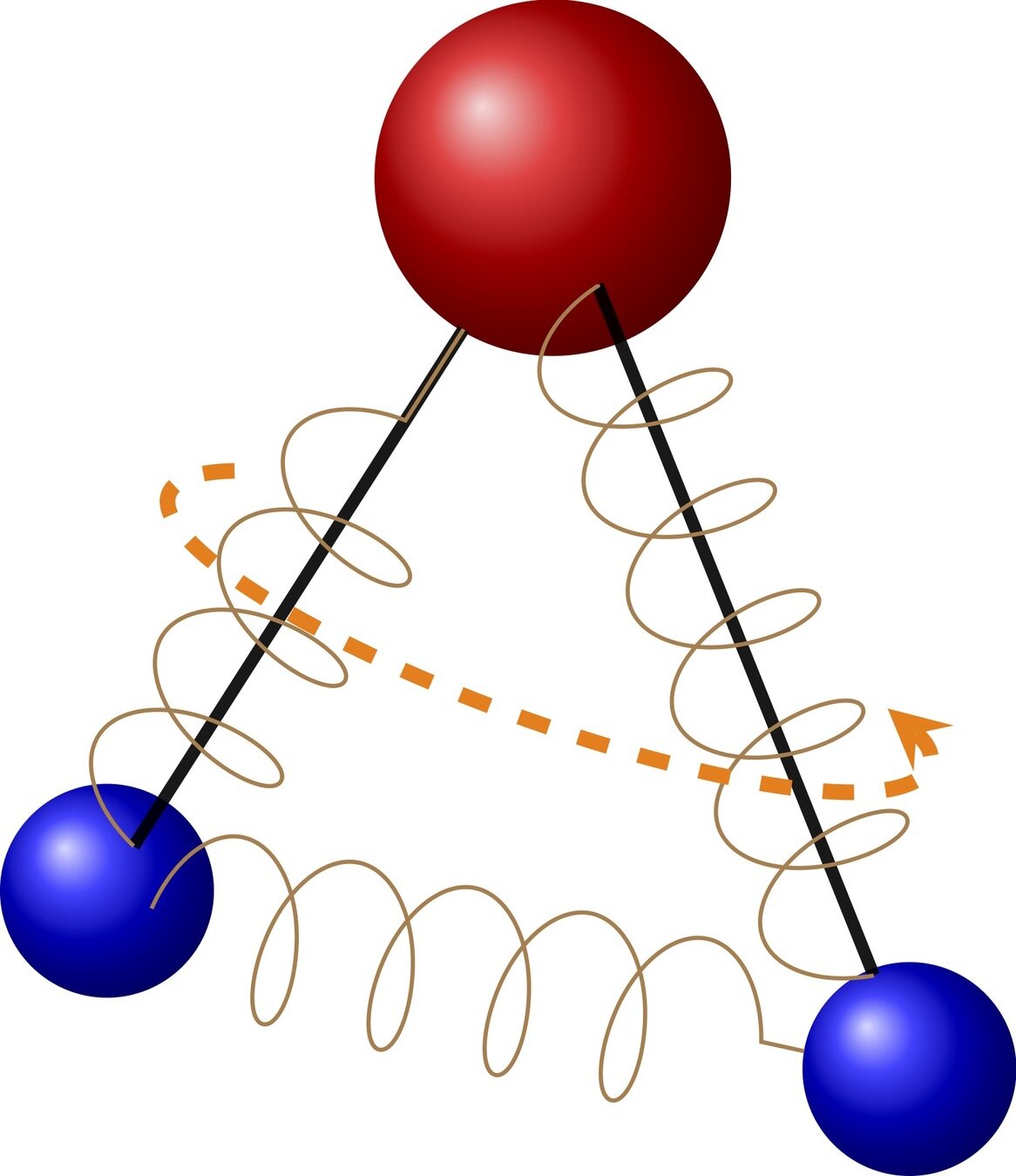
Statistical description of a monoatomic gas

[A. Greg: Kinetic theory of gases, wikipedia.]

\partial_t f_{t,x}(v) + v \cdot \nabla_x f_{t,x}(v) = Q(f_{t,x})(v)

advection

collisions

(e.g. \(\mathrm{Ar} \) )

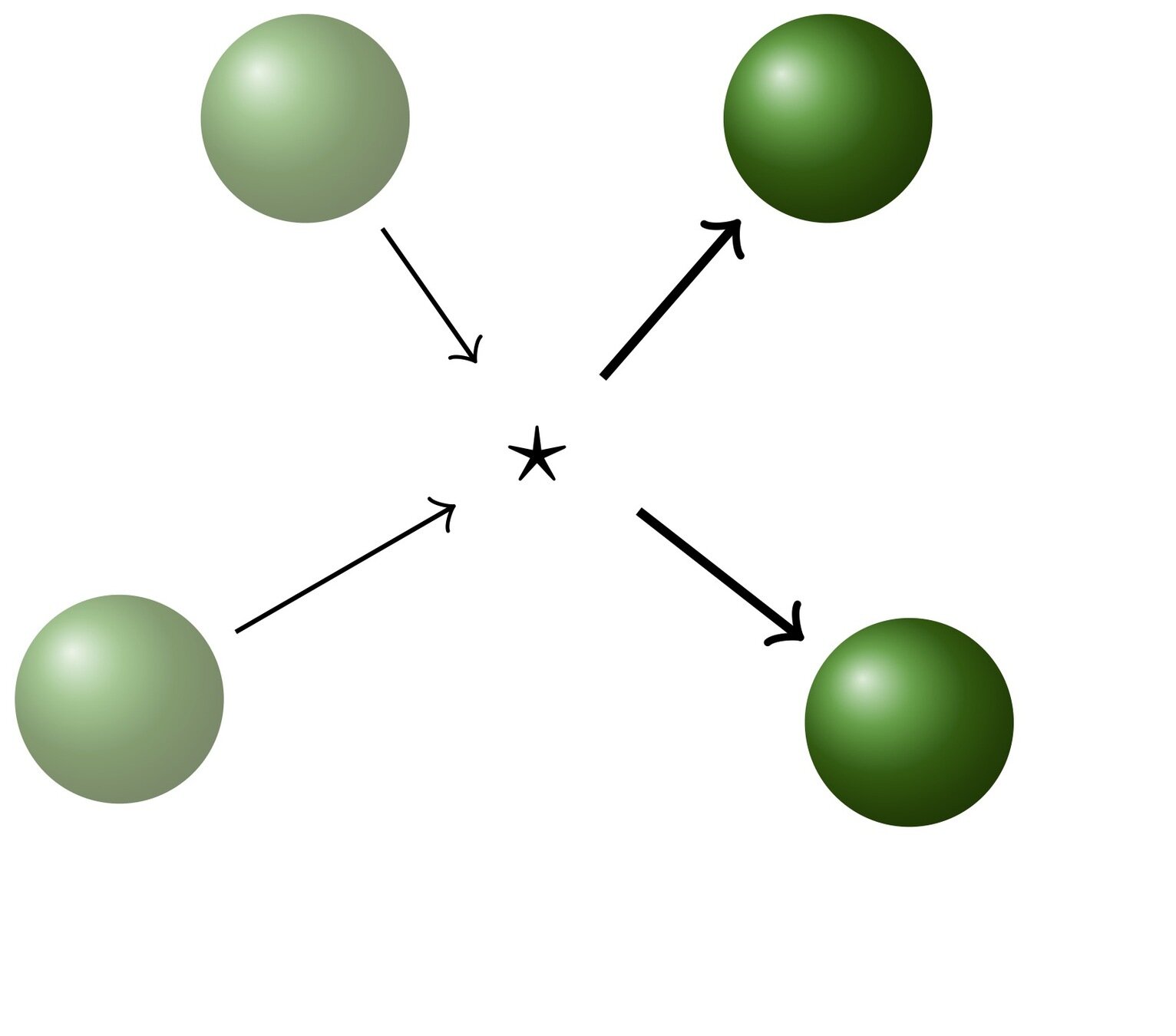
the collision operator

Q(f)(v) = \int_{v_*, \, v', \, v'_*} f(v') f(v'_*) - f(v) f(v_*)

v_*

v'_*

" "

General form

\begin{align*} v' = \frac{v+v_*}{2} + \frac{|v-v_*|}{2} \sigma \\ v'_* = \frac{v+v_*}{2} - \frac{|v-v_*|}{2} \sigma\\ \end{align*}

\newcommand{\Sb}{\mathbb{S}} \sigma \in \Sb^2

\newcommand{\dd}{\mathrm{d}} \textcolor{black}{Q(f)(v) = }\iint_{\R^3 \times \mathbb{S}^2} \textcolor{black}{\big( f(v') f(v'_*) - f(v) f(v_*) \big)} \, B(v,v_*,\sigma) \, \dd \sigma \, \dd v_*

\newcommand{\Sb}{\mathbb{S}} \approx (v_*, \sigma) \in \R^3 \times \Sb^2

Conserved quantities

mass, momentum & energy

\begin{align*} v+v_*&=v'+v'_* \\ |v|^2 + |v_*|^2 &= |v'|^2 + |v'_*|^2 \\ \end{align*}

\(B\) satisfies symmetry & reversibility

sub-manifold of \((\R^3)^3\)

Density of molecules: \(f \equiv f_{t,x}(v)\)

The Boltzmann equation

Statistical description of a monoatomic gas

[A. Greg: Kinetic theory of gases, wikipedia.]

\partial_t f_{t,x}(v) + v \cdot \nabla_x f_{t,x}(v) = Q(f_{t,x})(v)

advection

collisions

[A. Greg: Kinetic theory of gases, wikipedia.]

Focus on collisions

the Homogeneous Boltzmann equation

Density of molecules: \(f_t(v)\)

\partial_t f_t(v) = Q(f_t)(v)

\(x \)

advection

\(+ \, v \cdot \nabla_x f\)

Entropy and equilibrium

f^{\rm in}

f_t \underset{t \to \infty}{\longrightarrow} c \, e^{-\frac{|v-\textcolor{blue}{u}|^2}{2 \textcolor{blue}{T}} }

\textcolor{blue}{u}

\textcolor{blue}{T}

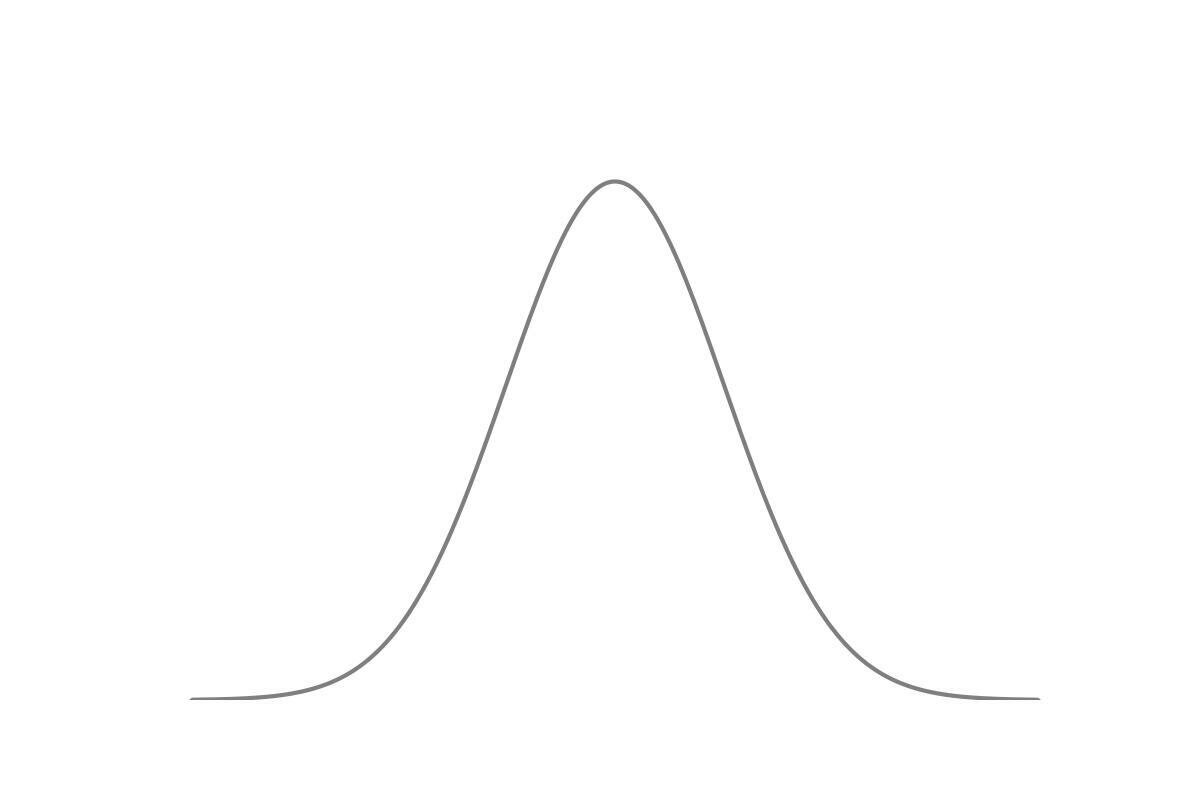
The Boltzmann entropy:

\newcommand{\dd}{\mathrm{d}} H (f) := \int_{\R^3} (f \log f - f)(v) \, \dd v

2. \(D(g) = 0 \iff g =M \) a Maxwellian:

characterization of equilibria

M(v) = \textcolor{blue}{\rho} \, Z(\textcolor{blue}{T})^{-1} \, \exp\left(-\frac{|v-\textcolor{blue}{u}|^2}{2 \textcolor{blue}{T}} \right)

\partial_t f_t(v) = Q(f_t)(v), \\ f_0 = f^{\rm in},

Boltzmann's H Theorem

1. If \(f \equiv f_t(v)\) solves

\(2^{\rm nd}\) principle of thermodynamics

\((HB)\)

then

\newcommand{\dd}{\mathrm{d}} \frac{\dd}{\dd t}H (f_t) = - D(f_t) \leq 0.

Illustration of the expected behaviour

Three linked concepts

Conserved quantities during collisions

(mass, momentum & energy)

Entropy functional

\newcommand{\dd}{\mathrm{d}} H(f)

Equilibrium distribution

(collision rules)

variants to the original model

original

monoatomic molecules

polyatomic

molecules

Part \(\mathrm{I}\)

Part \(\mathrm{I I}\)

polyatomic molecules

resonant collisions

fermions

Part \(\mathrm{III}\)

e.g. \(\mathrm{Ar}\)

e.g. \(\mathrm{H_2O}, \mathrm{N_2}\)

e.g. \(\mathrm{CO_2}\)

e.g. \(\mathrm{e^-}\)

outline

\(\mathrm{I}\). Boltzmann equation for polyatomic gases

\(\mathrm{II}\). Boltzmann equation for polyatomic gases with (quasi-)resonant collisions

\(\mathrm{III}\). Boltzmann-Fermi-Dirac equation

& contributions

- General modeling framework

- Relationships between models

- Compactness result in resonant setting

- Modelling & study of quasi-resonant Boltzmann

- Entropy/entropy production inequalities via a transfer method

- Relaxation to equilibrium with explicit rate

w/ Lods

w/ Boudin, Mathiaud, Salvarani

w/ Bisi, Groppi

[1,2]

[4]

[5]

[3]

[1] T. B., M. Bisi, M. Groppi: "A general framework for the kinetic modelling of polyatomic gases", Commun. Math. Phys., 2022.

[2] M. Bisi, T. B., M. Groppi: "An internal state kinetic model for chemically reacting mixtures of monatomic and polyatomic gases", Kinet. Relat. Models, 2024.

[3] T. B., L. Boudin, F. Salvarani: "Compactness property of the linearized Boltzmann operator for a polyatomic gas undergoing resonant collisions", J. Mat. Anal. Appl., 2023.

[4] T. B.: "Extending Cercignani's conjecture results from Boltzmann to Boltzmann-Fermi-Dirac equation", J. Stat. Phys., 2024.

[5] T. B., B. Lods: "Quantitative relaxation towards equilibrium for solutions to the Boltzmann-Fermi-Dirac equation with cutoff hard potentials", preprint, 2024.

Part \(\mathrm{I}\).

Boltzmann equation for polyatomic gases

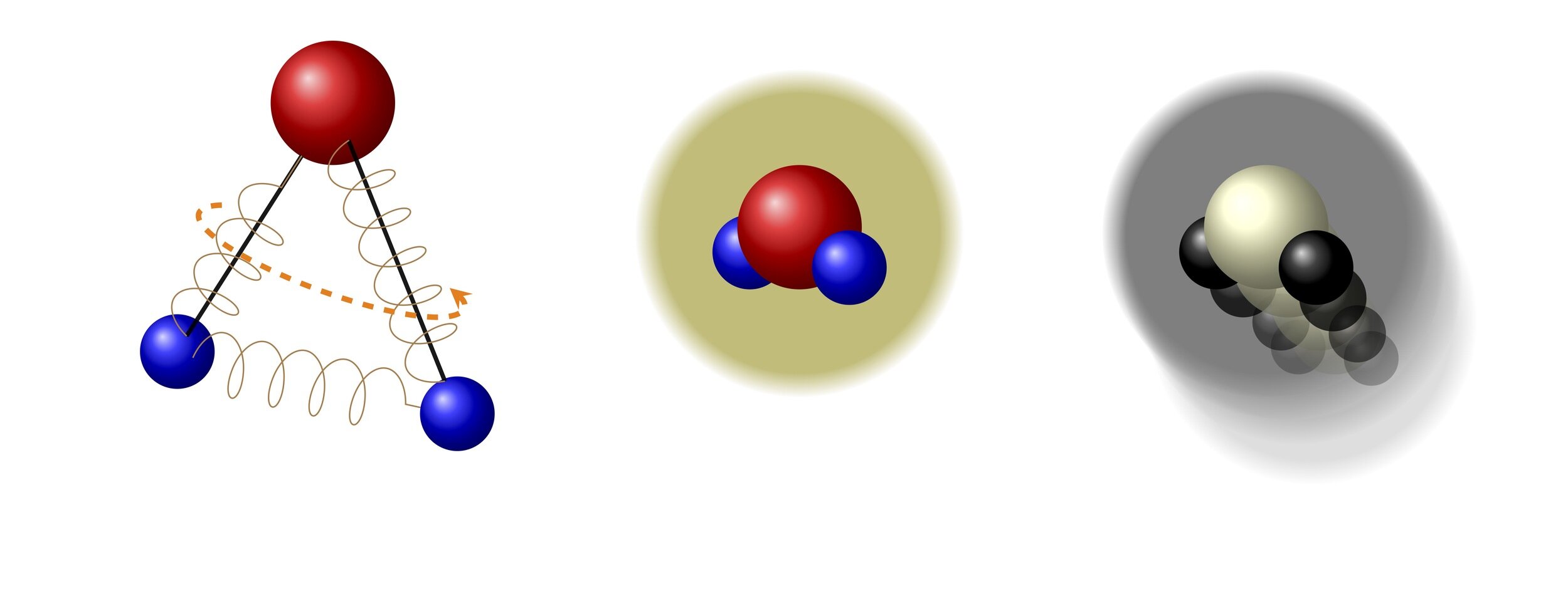
Pre-existing polyatomic models

2. Model with continuous

energy levels

[Borgnakke, Larsen, Desvillettes...]

1. Model with discrete

energy levels

[Bisi, Groppi, Spiga,...]

Internal energy

(rotation, vibration,...)

\(\{\epsilon_n\}_n\) energy levels

\(I \in \R_+\) energy level

integrate w.r.t. \(\varphi(I) \, \mathrm{d}I\)

rotation

vibration

rotation & vibration

rotation

rotation & vibration

vibration

integrate w.r.t. \(\varphi \textcolor{black}{(I) \, \mathrm{d} I}\)

Means

General modeling framework

Motivation

Provide a kinetic model taking rotation and vibration into account

with M. Bisi & M. Groppi

[1]

[2]

[1] T. B., M. Bisi, M. Groppi: "A general framework for the kinetic modelling of polyatomic gases", Commun. Math. Phys., 2022.

[2] M. Bisi, T. B., M. Groppi: "An internal state kinetic model for chemically reacting mixtures of monatomic and polyatomic gases", Kinet. Relat. Models, 2024.

General framework

setting
various paradigms

extension to Mixtures

validity for a mixture
chemical reactions

outline of part \(\mathrm{I}\)

A. General internal states framework

B. Probability theory interpretation & links between approaches

C. Extension to mixtures

general framework

\(\R^3 \times \textcolor{orange}{\R^3 \times \N \times \N \times \N}\)

internal structure of polyatomic molecules: rotation, vibration,...

\omega

n_1

n_2

n_3

(v,\textcolor{orange}{\omega, n_1, n_2, n_3})

\in

state of the molecule

space of states

energy of the molecule

\frac12 |v|^2 + \textcolor{orange}{\frac12 |\omega|^2 + n_1 E_1 + n_2 E_2 + n_3 E_3 + E_{pot}}

An example:

\(\R^3 \times \textcolor{orange}{\mathcal{E}}\)

internal structure of polyatomic molecules: general setting

(v,\textcolor{orange}{\zeta})

\in

state of the molecule

space of states

energy of the molecule

\frac12 |v|^2 + \textcolor{orange}{\varepsilon(\zeta)}

\newcommand{\E}{\mathcal{E}}

\zeta

measured space \((\mathcal{E}, \mu)\)

General framework's setting

v, \zeta

1. Microscopic state of the molecule:

Total energy of the molecule with state \((v, \zeta)\):

\frac12 |v|^2 + \varepsilon(\zeta)

\newcommand{\E}{\mathcal{E}}

velocity \(v \in \R^3\) and internal state \(\zeta \in \mathcal{E}\)

2. Space of internal states:

\(\varepsilon : \mathcal{E} \to \R\)

\newcommand{\E}{\mathcal{E}}

3. Internal energy function:

Assumptions

\(\varepsilon^0 := \text{inf ess}_{\mu} \;\varepsilon\) \(> -\infty\),

existence of fundamental energy level

finiteness of the partition function

\(\displaystyle \int_{\mathcal{E}} e^{-\beta \, \bar{\varepsilon}(\zeta)} \, \mathrm{d} \mu(\zeta)\) \(< +\infty\),

\(\forall \beta>0\)

\(\bar{\varepsilon} := \varepsilon - \varepsilon^0\) (\( : \mathcal{E} \to \R_+\))

(\partial_t + v \cdot \nabla_x) f_{t,x}(v,\textcolor{orange}{\zeta}) = Q(f_{t,x})(v,\textcolor{orange}{\zeta})

\(f \equiv f_{t,x}(v, \textcolor{orange}{\zeta})\) density of molecules

\textcolor{orange}{\zeta}

the polyatomic Boltzmann equation

Boltzmann equation:

v,\textcolor{orange}{\zeta}

v_*,\textcolor{orange}{\zeta_*}

v',\textcolor{orange}{\zeta'}

v'_*,\textcolor{orange}{\zeta'_*}

Collision operator:

\newcommand{\dd}{\mathrm{d}} Q(f)(v,\textcolor{orange}{\zeta}) = \iint_{\R^3 \times \mathbb{S}^2} \textcolor{orange}{\iiint_{\mathcal{E}^3}} \left[f(v',\textcolor{orange}{\zeta'}) f(v'_*,\textcolor{orange}{\zeta'_*}) - f(v,\textcolor{orange}{\zeta}) f(v_*,\textcolor{orange}{\zeta_*}) \right] B \; \textcolor{orange}{\dd \mu^{\otimes 3}(\zeta_*,\zeta',\zeta'_*)} \, \dd v_* \, \dd \sigma

\begin{align*} v' = \frac{v+v_*}{2} + \textcolor{orange}{\sqrt{\Delta}} \; \sigma, \\ v'_* = \frac{v+v_*}{2} - \textcolor{orange}{\sqrt{\Delta}} \; \sigma,\\ \end{align*}

\newcommand{\Sb}{\mathbb{S}} \sigma \in \Sb^2

Conserved quantities

mass, momentum & energy

\begin{align*} v+v_*&=v'+v'_* \\ \frac12|v|^2 + \textcolor{orange}{\varepsilon(\zeta)} + \frac12|v_*|^2 + \textcolor{orange}{\varepsilon(\zeta_*)} &= \frac12|v'|^2 + \textcolor{orange}{\varepsilon(\zeta')} + \frac12|v'_*|^2 + \textcolor{orange}{\varepsilon(\zeta'_*)} \\ \end{align*}

\textcolor{orange}{\Delta} := \frac14 |v-v_*|^2 + \textcolor{orange}{\varepsilon(\zeta) + \varepsilon(\zeta_*) - \varepsilon(\zeta') - \varepsilon(\zeta'_*)}

Boltzmann polyatomic: H Theorem

\partial_t f_t(v,\zeta) = Q (f_t)(v,\zeta),

[Bisi, B., Groppi]

2. \(D(g) = 0 \iff g = \mathcal{M} \), a generalized Maxwellian:

characterization of equilibria

\mathcal{M}(v,\zeta) = \textcolor{blue}{\rho} \, Z(\textcolor{blue}{T})^{-1} \, \exp \left(-\frac{|v-\textcolor{blue}{u}|^2}{2 \textcolor{blue}{T}} - \frac{\bar{\varepsilon}(\zeta)}{\textcolor{blue}{T}} \right)

Gibbs

Polyatomic (general setting) H Theorem

1. If \(f \equiv f_t(v,\zeta)\) solves

\(2^{\rm nd}\) principle of thermodynamics

then

\newcommand{\dd}{\mathrm{d}} \frac{\dd}{\dd t}H (f_t) = - D(f_t) \leq 0,

\newcommand{\dd}{\mathrm{d}} H(g) = \iint_{\R^3 \times \mathcal{E}} \{g \log g-g\} (v,\zeta) \, \dd v \, \dd \mu(\zeta)

Boltzmann entropy:

various Approaches and relationships

a parallel with probability theory

polyatomic internal structure

probability theory setting

\( (\Omega, \; \mathbb{P}) \) space of events

\( X : \Omega \to \R \) real random var.

\( (\mathcal{E}, \; \mu) \) space of internal states

\( \bar{\varepsilon} : \mathcal{E} \to \R_+ \) energy function

\( \bar{\varepsilon} = \varepsilon - \inf \varepsilon \)

\( (\R, \, \mathbb{P}_X)\) space of outcomes

\( \mathbb{P}_X\) on \(\R\) law of \(X\)

\( (\R_+, \, \mu_{\bar{\varepsilon}}) \) space of energy levels

\( \mu_{\bar{\varepsilon}}\) on \(\R_+\) energy law

\( ((0,1), \, \mathrm{Leb}) \) space of quantiles

\( F^{-1}_{\mathbb{P}_X}: (0,1) \to \R\) quantile function

\( ((0,\mu(\mathcal{E})), \, \mathrm{Leb}) \) space of energy quantiles

\( F^{-1}_{\mu_{\bar{\varepsilon}}}: (0,\mu(\mathcal{E})) \to \R_+\) energy quantile func.

Link with pre-existing models

\(\varphi\) can then be computed "ab initio"

\( (\R_+, \, \mu_{\bar{\varepsilon}}) \) space of energy levels

\( \mu_{\bar{\varepsilon}}\) on \(\R_+\) energy law

1. \(\mu_{\bar{\varepsilon}}\) is a discrete measure

supported on \(\{\epsilon_n\}_n\)

(\R_+, \, \mu_{\bar{\varepsilon}}) \, \longleftrightarrow \, (\N, \, \mathrm{count})

model with discrete energy levels

[Bisi, Groppi, Spiga,...]

with energy levels \(\{\epsilon_n\}_n\)

2. \(\mu_{\bar{\varepsilon}}\) has a density \(\varphi\) w.r.t.

Lebesgue measure

(\R_+, \, \mu_{\bar{\varepsilon}}) = (\R_+, \, \varphi(I) \mathrm{d}I)

model with continuous energy levels

[Borgnakke, Larsen, Desvillettes...]

(\R_+, \, \mu_{\bar{\varepsilon}}) = (\R_+, \, \textcolor{red}{\varphi}(I) \mathrm{d}I)

internal state

internal energy level

internal energy quantile

Paradigms and their use

\(\zeta \in \mathcal{E}\)

\(\mu\)

\(\varepsilon\)

\( I \in \R_+\)

\(\mu_{\bar{\varepsilon}}\)

\( q \in \R_+\)

\(\mathrm{Id}_{\R_+}\)

\(F_{\mu_{\bar{\varepsilon}}}^{-1}\)

Lebesgue

variable

measure

energy function

Physical modeling
General proofs

Explicit computations

Numerical simulations

(particle-based)

internal state

internal energy level

internal energy quantile

Paradigms and their use

Construct

Analyse

Simulate

mixtures with chemical reactions

2. Characterization of equilibria

H Theorem

1. \(2^{nd}\) principle of thermodynamics

3. Mass-action law

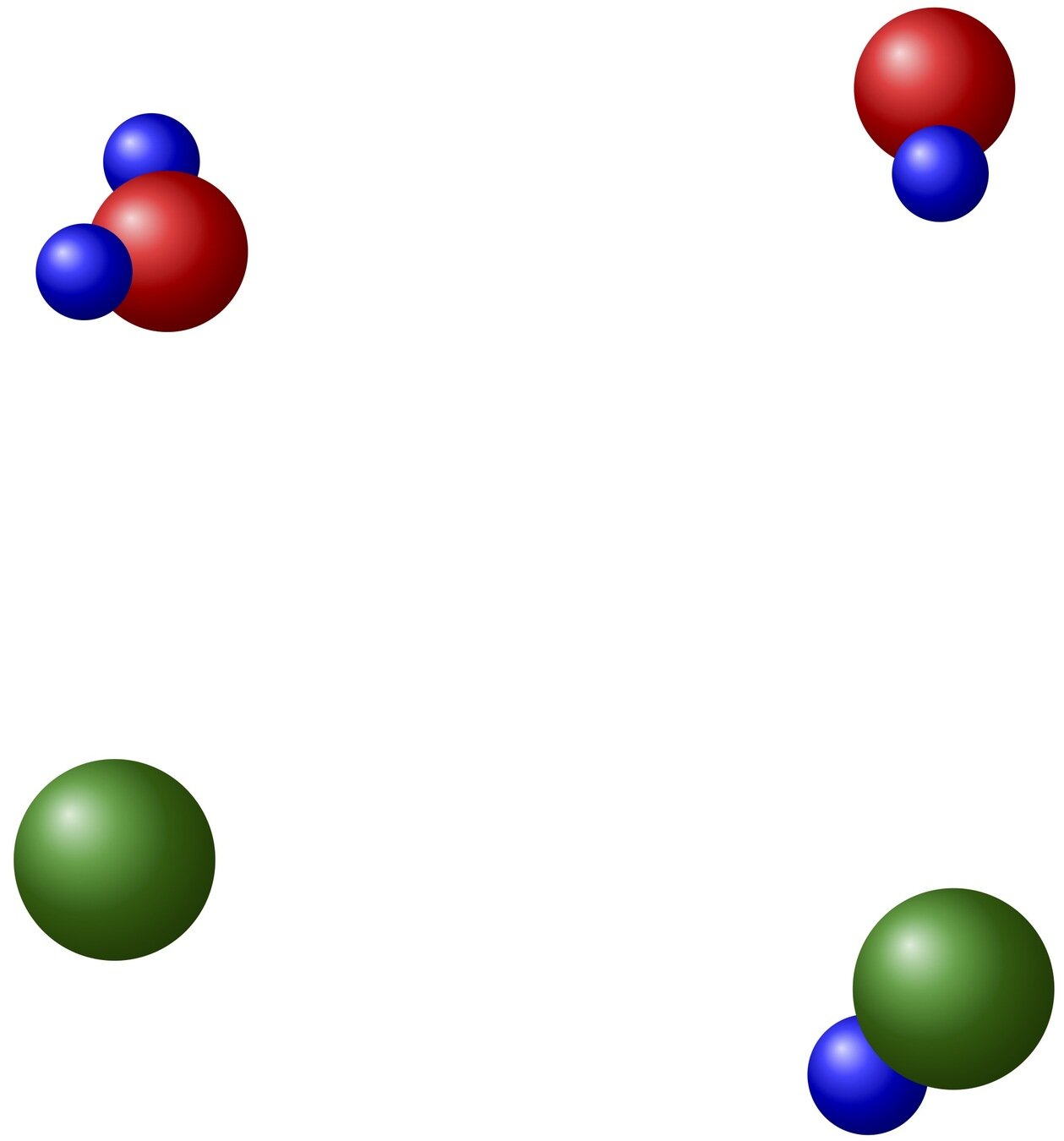
extension to mixtures with chemical reactions

\(\bullet\) models \((\mathcal{E_i},\mu_i)\) and \(\varepsilon_i\) for \(i = 1, \dots, N \)

\(\bullet\) study \(f \equiv (f_i)_i\), with \( f_i : \R^3 \times \mathcal{E}_i \to \R_+ \)

\(\bullet\) system of Boltzmann equations

\partial_t f_i + v \cdot \nabla_x f_i = Q(f)

\forall \, i,

collisions &

chemical reactions

Energy of reaction:

\Delta E = \varepsilon^0_k + \varepsilon^0_{\ell} - \varepsilon^0_i - \varepsilon^0_j

\ell

v \; \, \; \; \; \; \zeta

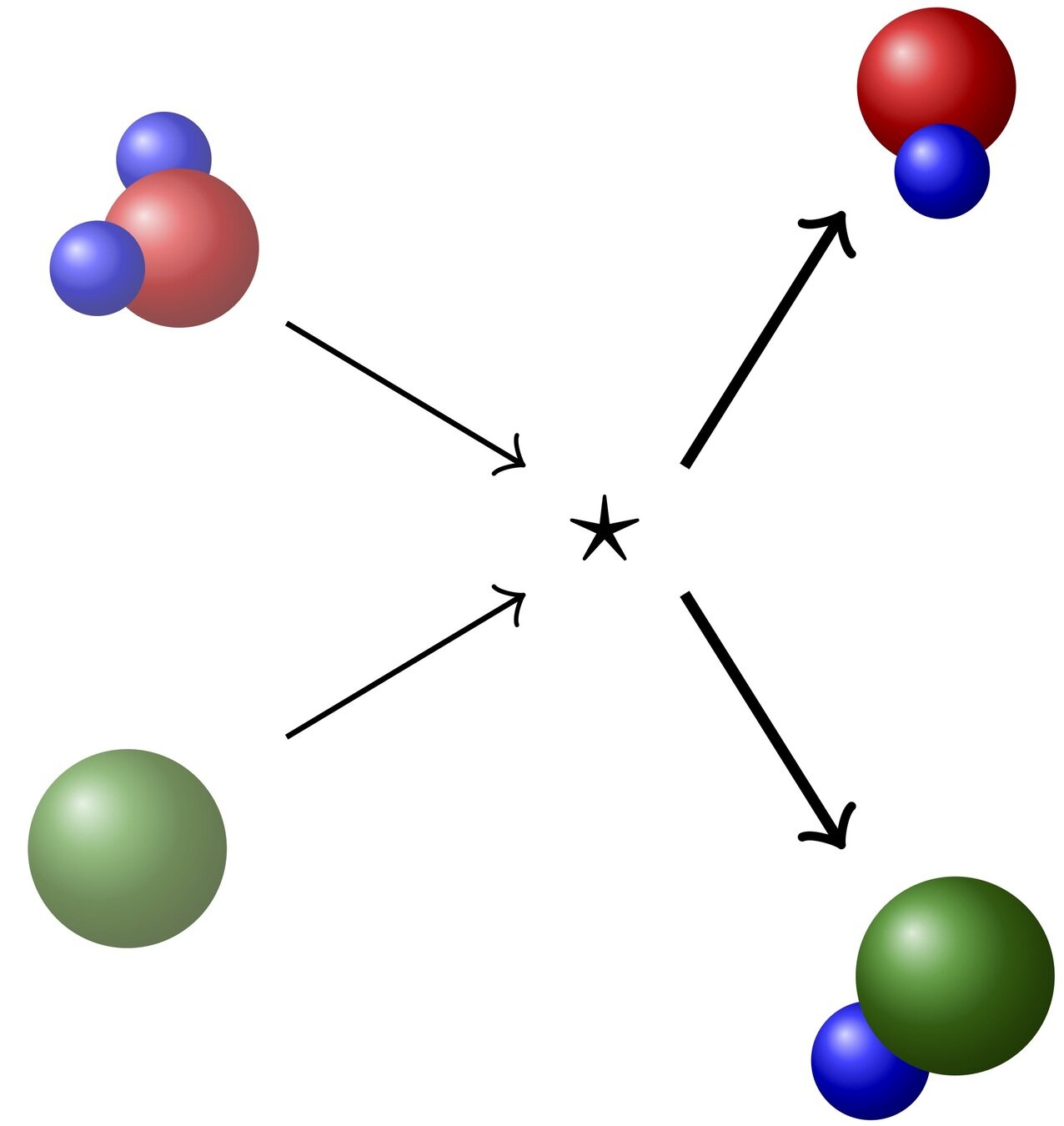
[Bisi, B., Groppi]

\(\varepsilon^0 := \text{inf ess}_{\mu} \;\varepsilon\)

Part \(\mathrm{II}\).

Boltzmann equation for polyatomic gases with

(quasi-)resonant collisions

Context

Resonant collisions for some polyatomic molecules (e.g. CO\(_2\) )

compactness result

[3]

[3] T. B., L. Boudin, F. Salvarani: "Compactness property of the linearized Boltzmann operator for a polyatomic gas undergoing resonant collisions", J. Mat. Anal. Appl., 2023.

with Boudin, Mathiaud, Salvarani

with Boudin, Salvarani

Lines of work

Near-equilibrium for resonant polyatomic gas
Model & study quasi-resonant gas

Near Equilibrium

resonant

linearized Boltzmann operator

quasi-resonant

model quasi-resonance
behavior of the dynamic
numerical validation

A. Boltzmann model with resonant collisions

B. Boltzmann model with quasi-resonant collisions

outline of part \(\mathrm{II}\)

C. Relaxation of temperatures and Landau-Teller equations

A. Boltzmann with resonant collisions

Boltzmann model with resonant collisions (1)

\renewcommand{\R}{\mathbb{\R}}

I \in \R_+, \quad \varphi(I) \mathrm{d}I

continuous internal energy levels model

\textcolor{olive}{I}

conservations for a resonant collision

separate conservation of kinetic and internal energies

v,I

v_*,I_*

v',I'

v'_*,I'_*

\newcommand{\Sb}{\mathbb{\mathbb{S}}}

\newcommand{\Sb}{\mathbb{S}}

uncoupling of \(v\) and \(I\)

\begin{align*} I+I_* &= I' + I'_* \end{align*}

\begin{align*} v+v_*&=v'+v'_* \\ |v|^2 + |v_*|^2 &= |v'|^2 + |v'_*|^2 \end{align*}

Resonant collision operator

Q^{\rm res} (f)(v,I) = \iint_{\R^3 \times \mathbb{S}^2} \iint_{(\R_+)^{\textcolor{red}{2}}} \big[ f' f'_* - f f_* \big] \times B^{\rm res} \times \textcolor{red}{\varphi(I+I_* - I')\,\varphi(I') \, \mathrm{d} I'} \, \varphi(I_*) \, \mathrm{d} I_* \, \mathrm{d} v_* \, \mathrm{d} \sigma

f \equiv f(v,I)

I'_*

Boltzmann with resonant collisions: H Theorem

\partial_t f_t(v,I) = Q^{\rm res} (f_t)(v,I),

[Boudin, Rossi, Salvarani]

2. \(D^{\rm res}(g) = 0 \iff g = M^{\rm res} \), a two-temperature Maxwellian:

characterization of equilibria

M^{\rm res}(v,I) = \textcolor{blue}{\rho} \, Z(\textcolor{blue}{T_k},\textcolor{blue}{T_i})^{-1} \, \exp \left(-\frac{|v-\textcolor{blue}{u}|^2}{2 \textcolor{blue}{T_k}} - \frac{I}{\textcolor{blue}{T_i}} \right)

Polyatomic resonant H Theorem

1. If \(f \equiv f_t(v,I)\) solves

\(2^{\rm nd}\) principle of thermodynamics

then

\newcommand{\dd}{\mathrm{d}} \frac{\dd}{\dd t}H (f_t) = - D^{\rm res}(f_t) \leq 0.

\newcommand{\dd}{\mathrm{d}} H(g) = \iint_{\R^3 \times \R_+} \{g \log g-g\} (v,I) \, \dd v \, \varphi(I) \, \dd I

Boltzmann entropy:

compactness result of the linearized resonant Boltzmann operator

resonant collision operator \(Q(f)\)

linearize around equilibrium

resonant linearized operator \(\mathcal{L}f\)

\mathcal{L} = K - \nu \mathrm{Id}

[T.B., Boudin, Salvarani]

Theorem. \(K\) compact operator of \(L^2(\R^3 \times \R_+, \mathrm{d} v \, \varphi(I) \, \mathrm{d}I)\)

useful for

existence & uniqueness close-to-equilibrium
study of the spectrum

Proof strategy:

split the study into kinetic & internal parts
kinetic part \(\leftrightarrow\) monoatomic (+improvement)

BONUS: a nice change of variables in the sphere (variant to Grad's proof / compactness monoatomic)

\newcommand{\Sb}{\mathbb{S}} (\sigma_1, \sigma_2) \; \in \Sb^2 \times \Sb^2 \quad \mapsto \quad \left(z = \frac{\sigma_1 + \sigma_2}{2} , \; A \right) \; \in \mathcal{B}_{\R^3}(0,1) \times \Sb^1

\newcommand{\Sb}{\mathbb{S}} \newcommand{\dd}{\mathrm{d}} \iint_{\Sb^2 \times \Sb^2} \varphi \left( \frac{\sigma_1 + \sigma_2}{2} \right) \, \dd \sigma_1 \, \dd \sigma_2 = \iint_{\mathcal{B}_{\R^3}(0,1) \times \Sb^1} \varphi(z) \, \textcolor{brown}{4|z|^{-1}} \, \dd z \, \dd A

\newcommand{\Sb}{\mathbb{S}}

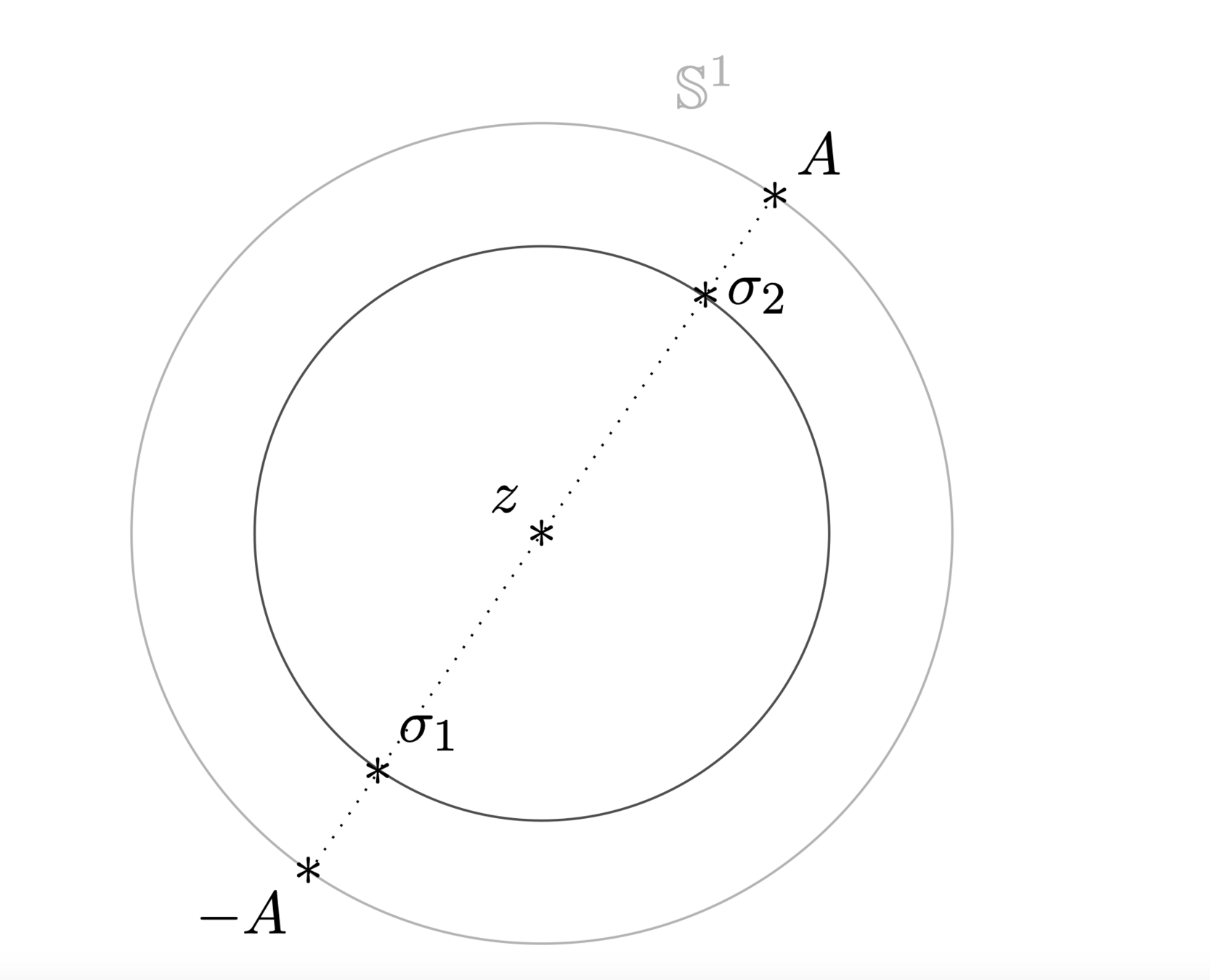
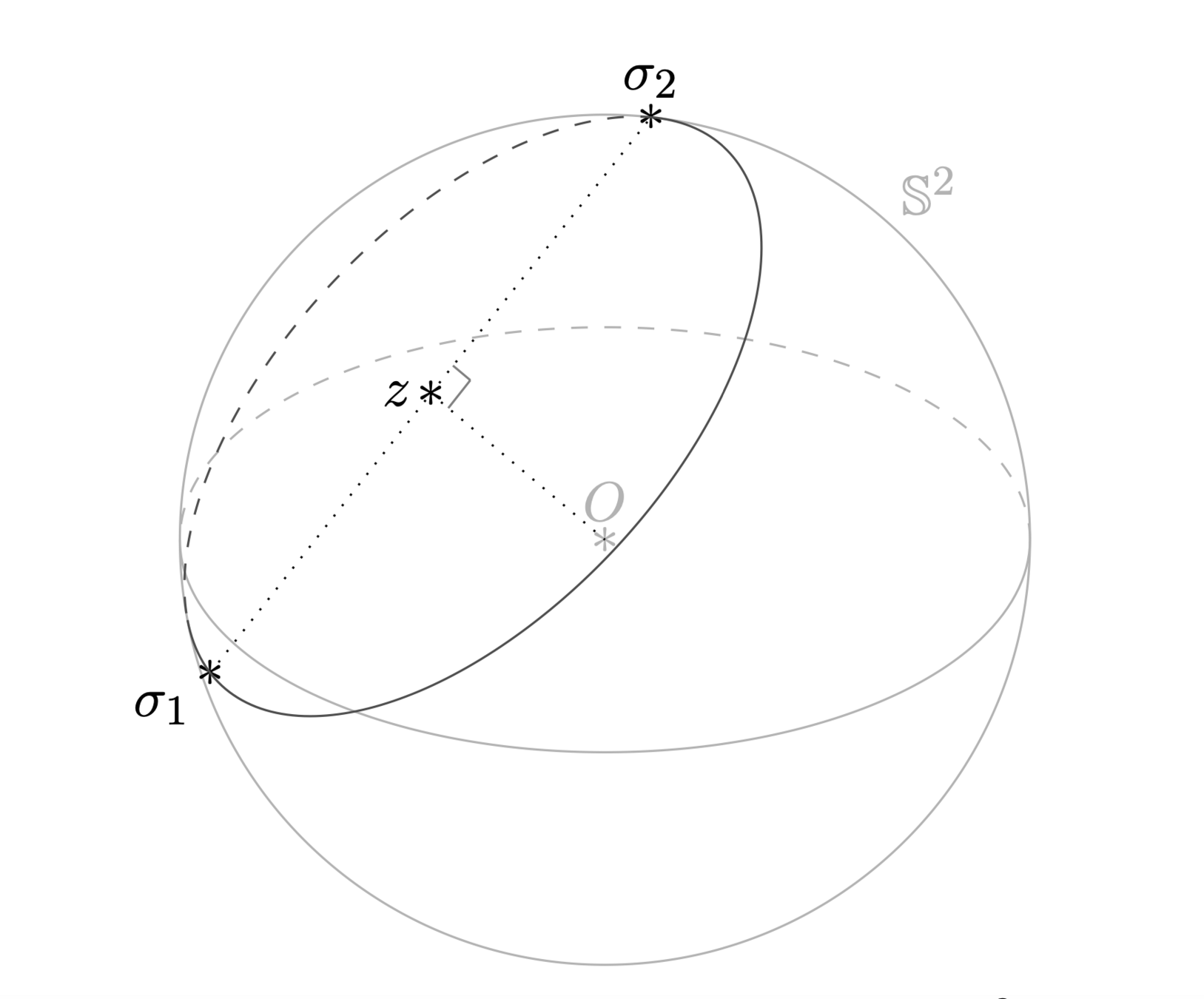
Recap Features of the resonant model

\(\bullet\) Separation of kinetic and internal energies

\(\bullet\) Two temperatures (kinetic & internal) at equilibrium

B. Boltzmann with quasi-resonant collisions

Notion of quasi-resonant collisions

conservations for a quasi-resonant collision

how to make this rigorous?

\begin{align*} I+I_* &\approx I' + I'_* \end{align*}

\begin{align*} v+v_*&=v'+v'_* \\ \frac12|v|^2 + I + \frac12|v_*|^2 + I_* &=\frac12|v'|^2 + I' + \frac12|v'_*|^2 + I'_* \end{align*}

v,I

v_*,I_*

v',I'

v'_*,I'_*

\begin{align*} v+v_*&=v'+v'_* \\ \frac12|v|^2 + I + \frac12|v_*|^2 + I_* &=\frac12|v'|^2 + I' + \frac12|v'_*|^2 + I'_* \end{align*}

(v,v_*,v',v'_*, I,I_*,I',I'_*) \in (\R^3)^4 \times (\R_+)^4 \; \; \text{such that}

\begin{align*} I+I_* &= I' + I'_* \end{align*}

Set of allowed collisions in the

resonant polyatomic case

our model for quasi-resonant collisions

v,I

v_*,I_*

v',I'

v'_*,I'_*

sub-manifold \(\mathcal{V}_0\) with 1 dimension less than \(\mathcal{V}\)

B^{\textcolor{red}{\text{res}}} \longleftrightarrow B^{\rm \textcolor{grey}{standard}} \times \mathbf{\delta}_{\textcolor{red}{\mathcal{V}_0}}

Resonant collision kernel

manifold \(\mathcal{V} \subset (\mathbb{R}^3)^4 \times (\mathbb{R}_+)^4\)

0 < \lambda \ll 1

\begin{align*} I+I_* &\approx I' + I'_* \end{align*}

Set of allowed collisions in the

quasi-resonant case

manifold \(\mathcal{V} \subset (\mathbb{R}^3)^4 \times (\mathbb{R}_+)^4\)

(v,v_*,v',v'_*, I,I_*,I',I'_*) \in (\R^3)^4 \times (\R_+)^4 \; \; \text{such that}

sub-manifold \(\mathcal{V}_{\lambda}\) with same dimension as \(\mathcal{V}\)

our model for quasi-resonant collisions

v,I

v_*,I_*

v',I'

v'_*,I'_*

\begin{align*} v+v_*&=v'+v'_* \\ \frac12|v|^2 + I + \frac12|v_*|^2 + I_* &=\frac12|v'|^2 + I' + \frac12|v'_*|^2 + I'_* \end{align*}

e^{-\lambda} \leqslant \frac{\left(\frac{I+I}{\frac14|v-v_*|^2}\right) }{ \left(\frac{I'+I'}{\frac14|v'-v'_*|^2} \right)} \leqslant e^{\lambda}

B^{\textcolor{red}{\text{quasi-res}}}_{\textcolor{red}{\lambda}} \longleftrightarrow B^{\rm \textcolor{grey}{standard}} \times \frac{\mathbf{1_{\textcolor{red}{\mathcal{V}_{\lambda}}}}}{|\textcolor{red}{\mathcal{V}_{\lambda}}|}

Quasi-resonance encoded in the collision kernel

\(\lambda > 0\) quasi-resonance parameter

our model for quasi-resonant collisions

\newcommand{\dd}{\mathrm{d}} Q^{\textcolor{red}{\text{quasi-res}}}_{\textcolor{red}{\lambda}}(f)(v,I) = \iint_{\R^3 \times \mathbb{S}^2} \iiint_{(\R_+)^3} \big[ f' f'_* - f f_* \big] \times B^{\textcolor{red}{\text{quasi-res}}}_{\textcolor{red}{\lambda}} \times \varphi(I'_*) \, \dd I'_* \, \varphi(I') \, \dd I' \, \varphi(I_*) \, \dd I_* \, \dd v_* \, \dd \sigma

B^{\textcolor{red}{\text{quasi-res}}}_{\textcolor{red}{\lambda}} = B^{\rm \textcolor{grey}{standard}} \times c(\cdot) \frac{\mathbf{1_{\textcolor{red}{\mathcal{V}_{\lambda}}}}}{\textcolor{red}{\lambda}}

\mathcal{V}_{\lambda} : \qquad e^{-\lambda} \leqslant \frac{\left(\frac{I+I}{\frac14|v-v_*|^2}\right) }{ \left(\frac{I'+I'}{\frac14|v'-v'_*|^2} \right)} \leqslant e^{\lambda}

Family of collision kernels:

Family of collision operators:

\forall \lambda > 0,

Resonant asymptotics

Q^{\textcolor{red}{\text{quasi-res}}}_{\textcolor{red}{\lambda}}(f) \underset{\textcolor{red}{\lambda} \to 0}{\longrightarrow} Q^{\rm res} (f),

Q^{\rm res} (f)(v,I) = \iint_{\R^3 \times \mathbb{S}^2} \iint_{(\R_+)^2} \big[ f' f'_* - f f_* \big] \times B^{\rm res} \times \varphi(I+I_* - I')\,\varphi(I') \, \mathrm{d} I' \, \varphi(I_*) \, \mathrm{d} I_* \, \mathrm{d} v_* \, \mathrm{d} \sigma,

B^{\rm res} = B^{\rm \textcolor{grey}{standard}} (I'_* = I+I_* - I')

associated resonant model

2. Equilibria: one-temperature Maxwellian:

\mathcal{M}(v,I) = \textcolor{blue}{\rho} \, Z(\textcolor{blue}{T})^{-1} \, \exp \left(-\frac{|v-\textcolor{blue}{u}|^2}{2 \textcolor{blue}{T}} - \frac{I}{\textcolor{blue}{T}} \right)

1. \(2^{nd}\) principle of thermodynamics

Quasi-resonant H Theorem

H Theorem for quasi-resonant collisions

same as standard polyatomic

Boltzmann with quasi-resonant collisions: properties

Conjecture

If \(f\) solution to the quasi-resonant Boltzmann equation with parameter \(\lambda\) "small" enough, then

time

\(T_i\) & \(T_k\) relax to each other

\(f\) (almost) stays a two-temperature Maxwellian (\(T_i\) & \(T_k\))

\(f\) relaxes to a two-temperature Maxwellian

short-time

long-time

derivation of explicit ODE:

Landau-Teller

Two main properties:

1. Quasi-resonant dynamic \(\sim\) resonant dynamic /

2. Quasi-resonant equilibrium : one temperature

resonant equilibrium: two temperatures

LANdau-Teller and numerical validation

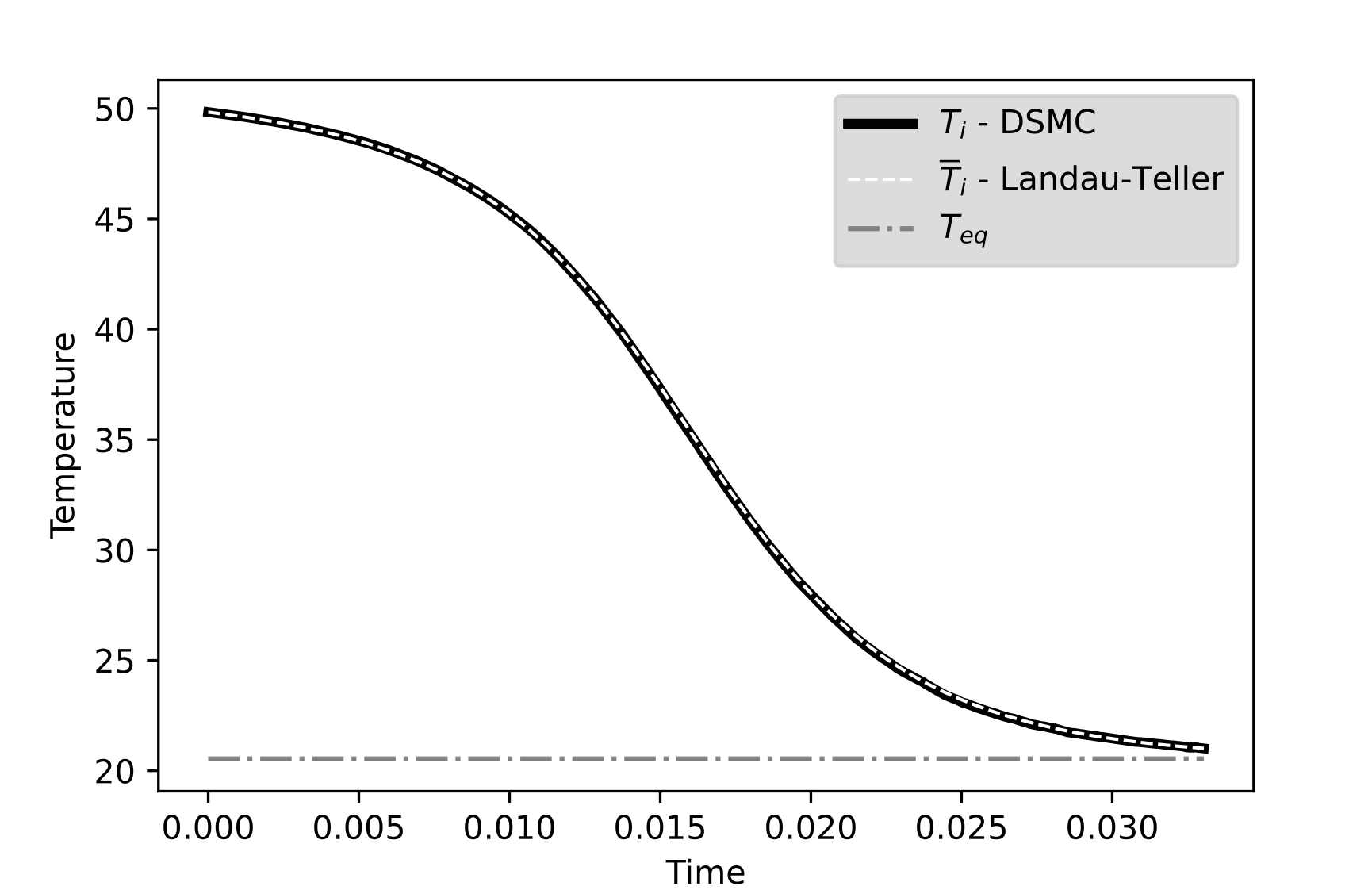
parameters: \(\lambda = 0.1\), \(T_i^0 = 50\), \(T_k^0 = 1\), \(T_{eq} = 20.6\)

relative \(L^2\) error \(\sim 10^{-3}\)

Numerical experiment

Simulate Boltzmann with DSMC : \(T_i\)

Solve Landau-Teller : \(\overline{T}_i\)

Landau-Teller equations:

\begin{align*} \overline{T_i}'(t) &= \textcolor{red}{\lambda^2} \, \mathcal{c}(\overline{T_i},\overline{T_k}) \, (\overline{T_k} - \overline{T_i}) \\ \overline{T_k}'(t) &= \textcolor{red}{\lambda^2} \, \mathcal{c'}(\overline{T_i},\overline{T_k}) \, (\overline{T_i} - \overline{T_k}) \end{align*}

T_i,T_k \approx \overline{T}_i, \overline{T}_k

For a quasi-resonant dynamic:

with \(\lambda\) "small"

for a certain class of collision kernels

perspective

Asymptotic-Preserving (AP) scheme

To simulate the quasi-resonant Boltzmann equation with parameter \(\lambda\) "small",

time

\(t_0\)

\(\mathcal{O}(\lambda^{-2})\)

Get \(T_i\) & \(T_k\) by solving the corresponding Landau-Teller system

Take the solution to be a two-temperature Maxwellian (\(T_i\) & \(T_k\))

Simulate the corresponding resonant Boltzmann equation

numerically cheap

numerically expensive

Sources of error:

Shape of the distribution (not exactly a two-temperature Maxwellian)
Higher order terms in \(\lambda\) (Taylor expansion) for Landau-Teller equation
Finite number of numerical particles

theoretical

numerical

Part \(\mathrm{III}\).

Boltzmann-Fermi-Dirac equation

Means

Entropy methods: functional inequalities

\implies

known

new!

Motivation

Explicit rate of relaxation to equilibrium for solutions to the Boltzmann-Fermi-Dirac equation

entropy inequality

classic Boltzmann

entropy inequality

Boltzmann-Fermi-Dirac

explicit rate of relaxation to equilibrium

with B. Lods

[5]

[4]

[4] T. B.: "Extending Cercignani's conjecture results from Boltzmann to Boltzmann-Fermi-Dirac equation", J. Stat. Phys., 2024.

[5] T. B., B. Lods: "Quantitative relaxation towards equilibrium for solutions to the Boltzmann-Fermi-Dirac equation with cutoff hard potentials", preprint, 2024.

Entropies

to equilibrium

A. The Boltzmann-Fermi-Dirac equation

C. Transfer of entropy inequalities

B. Entropy methods and relaxation to equilibrium

outline of part \(\mathrm{III}\)

D. Relaxation to equilibrium for Boltzmann-Fermi-Dirac

a. the Boltzmann-fermi-dirac equation

(\partial_t + v \cdot \nabla_x) f_{t,x}(v) = Q_{\textcolor{purple}{\delta}}(f_{t,x})(v)

\(f \equiv f_{t,x}(v)\) density of fermions

BFD equation:

the Boltzmann-Fermi-Dirac equation

Q_{\color{purple} \delta}(f)(v) = \iint_{\R^3 \times \mathbb{S}^2} \left[f' f'_* \textcolor{purple}{(1 - \delta f) (1-\delta f_*)} - f f_* \textcolor{purple}{(1 - \delta f')(1-\delta f'_*)} \right] B \; \mathrm{d} v_* \, \mathrm{d} \sigma

Collision operator:

\begin{align*} v' = \frac{v+v_*}{2} + \frac{|v-v_*|}{2} \sigma \\ v'_* = \frac{v+v_*}{2} - \frac{|v-v_*|}{2} \sigma\\ \end{align*}

\newcommand{\Sb}{\mathbb{S}} \sigma \in \Sb^2

Conserved quantities

mass, momentum & energy

\begin{align*} v+v_*&=v'+v'_* \\ |v|^2 + |v_*|^2 &= |v'|^2 + |v'_*|^2 \\ \end{align*}

Pauli exclusion principle

quantum parameter \(\textcolor{purple}{\delta} > 0\)

0 \leq f_{t,x} \leq \frac{1}{\textcolor{purple}{\delta}}

2 fermions cannot occupy the same state

v_*

v'_*

Boltzmann-fermi-dirac: H Theorem

\partial_t f_t(v) = Q_{\textcolor{purple}{\delta}} (f_t)(v),

2. \(D_{\textcolor{purple}{\delta}}(g) = 0 \iff g = M_{\textcolor{purple}{\delta}} \), a Fermi-Dirac statistics:

characterization of equilibria

Boltzmann-Fermi-Dirac H Theorem

1. If \(f \equiv f_t(v)\) solves

\(2^{\rm nd}\) principle of thermodynamics

then

\newcommand{\dd}{\mathrm{d}} \frac{\dd}{\dd t}H_{\textcolor{purple}{\delta}} (f_t) = - D_{\textcolor{purple}{\delta}}(f_t) \leq 0,

\newcommand{\dd}{\mathrm{d}} H_{\textcolor{purple}{\delta}}(g) = \int_{\R^3} \{g \log g +\textcolor{purple}{\delta}^{-1} (1- \textcolor{purple}{\delta} g) \log (1- \textcolor{purple}{\delta} g)\} (v) \, \dd v

\displaystyle M_{\textcolor{purple}{\delta}}(v) = \frac{\displaystyle e^{\textcolor{blue}{a} - \textcolor{blue}{b}|v-\textcolor{blue}{u}|^2}} {\displaystyle 1 + \textcolor{purple}{\delta} e^{\textcolor{blue}{a} - \textcolor{blue}{b}|v-\textcolor{blue}{u}|^2}}

\frac{1}{\textcolor{purple}{\delta}}

\textcolor{blue}{u}

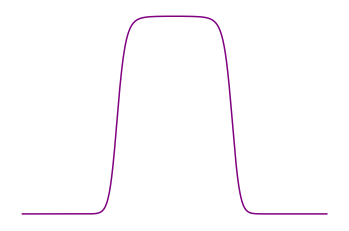
\(\searrow T°\)

\( T°=T_{\min}\)

or saturated state

\displaystyle F_{\textcolor{purple}{\delta}}(v) = \frac{1}{\textcolor{purple}{\delta}} \; \mathbf{1}_{\mathcal{B}(\textcolor{blue}{u},\textcolor{blue}{r}_{\textcolor{purple}{\delta}})}

Fermi-Dirac entropy:

- Existence & stability of solutions to homogeneous BFD for cutoff hard potentials

[Lu, Wennberg]

Existence and uniqueness of solutions to inhomogeneous BFD for cutoff kernels

[Dolbeault]

- Relaxation to equilibrium of such solutions:

either \(f_0 =\) or \(f_t \; \underset{t \to \infty}{\overset{L^1}{\rightharpoonup}}\)

Derivation of the equation from particles system (partially formal)

[Benedetto, Castella, Esposito, Pulvirenti]

at which rate?

some results on bfd

saturated state

Fermi-Dirac stat.

B. relaxation to equilibrium and entropy methods

entropy and equilibrium

entropy : \(\displaystyle H\)

equilibrium associated to \(f\): \(M^f\)

\textcolor{blue}{\text{mass}}(f),\textcolor{blue}{\text{momentum}}(f),\textcolor{blue}{\text{energy}}(f)

\(M^f = \argmin H \)

H(f|M^f) := H(f) - H(M^f) \geq 0

relative entropy to equilibrium

( of \(f\) )

"distance" to equilibrium

\partial_t f_t = Q(f_t)

\(t \mapsto H(f_t) \; \searrow \)

\partial_t f_t = Q(f_t)

Entropy dissipation \(D\)

\(D \) non-negative operator

Try to prove \(D(g) \gtrsim {H(g|M^g)}^{1+\alpha}\)

(functional inequality)

Entropy / entropy production inequality

To obtain \(H(f_t|M^{f_0}) \lesssim t^{-1/\alpha}\)

\displaystyle \frac{\mathrm{d}}{\mathrm{d} t} H(f_t|M^{f_0}) = - D(f_t)

Try to prove \(D(g) \gtrsim H(g|M^g)\)

To obtain \(H(f_t|M^{f_0}) \lesssim e^{-Ct} \)

(Grönwall)

Csiszar-Kullback-Pinsker

\|f_t - M^{f_0}\|_{L^1}^2 \lesssim H(f_t|M^{f_0})

entropy method

Fermi-Dirac entropy

Boltzmann entropy

H_{\textcolor{green}{0}}(g) = \int g \log g - g

H_{\textcolor{purple}{\delta}}(f) = \int f \log f + {\textcolor{purple}{\delta}}^{-1}\int (1 - {\textcolor{purple}{\delta}} f) \log (1-{\textcolor{purple}{\delta}} f)

M_{\textcolor{green}{0}}(v) = e^{a - b|v-u|^2}

\displaystyle M_{\textcolor{purple}{\delta}}(v) = \frac{e^{a - b|v-u|^2}}{1 + \textcolor{purple}{\delta} e^{a - b|v-u|^2}}

Equilibrium: Fermi-Dirac statistics

Equilibrium: Maxwellian

entropies and equilibria

Boltzmann

Boltzmann-Fermi-Dirac

Fermi-Dirac entropy

H_{\textcolor{green}{0}}(g) = \int \Phi_{\textcolor{green}{0}}(g(v)) \, \mathrm{d} v

H_{\textcolor{purple}{\delta}}(f) = \int \Phi_{\textcolor{purple}{\delta}}(f(v)) \, \mathrm{d} v

M_{\textcolor{green}{0}}(v) = (\Phi_{\textcolor{green}{0}}')^{-1} \left(\alpha + \beta \cdot v + \gamma |v|^2 \right)

\displaystyle M_{\textcolor{purple}{\delta}}(v) = (\Phi_{\textcolor{purple}{\delta}}')^{-1} \left(\alpha + \beta \cdot v + \gamma |v|^2 \right)

Equilibrium: Fermi-Dirac statistics

Equilibrium: Maxwellian

entropies and equilibria

Boltzmann

Boltzmann-Fermi-Dirac

\Phi_{\textcolor{purple}{\delta}}'(x) = \log \left(\frac{x}{1 - \textcolor{purple}{\delta} x} \right)

\Phi_{\textcolor{green}{0}}' = \log

entropy \(\displaystyle H : h \mapsto \int \Phi(h)\) \(\Phi\) \(\mathcal{C}^2\) st. convex

equilibrium

M = (\Phi')^{-1} (\alpha \, \textcolor{blue}{\text{mass}} + \beta \cdot \textcolor{blue}{\text{momentum}} + \gamma \, \textcolor{blue}{\text{energy}})

Boltzmann entropy

M = (\Phi')^{-1} (\textcolor{blue}{\text{something conserved}})

D_0(g) \gtrsim H_0(g|M_0^g)^{1 \textcolor{grey}{+ \alpha}}

Boltzmann

Toscani, Villani

D^L_0(g) \gtrsim H_0(g|M_0^g)^{1 \textcolor{grey}{+ \alpha}}

Landau

D^L_{\delta}(f) \gtrsim H_{\delta}(g|M_{\delta}^g)^{1 \textcolor{grey}{+ \alpha}}

LAndau-Fermi-Dirac

Desvillettes, Villani

Alonso, Bagland Desvillettes, Lods

D_{\delta}(f) \gtrsim H_{\delta}(g|M_{\delta}^g)^{1 \textcolor{grey}{+ \alpha}}

Boltzmann-FERMI-DIRAC

known entropy inequalities

C. transfer of inequalities

\forall \, g \in \mathcal{G}, \qquad D_0(g) \gtrsim H_0(g|M_0^g)^{1 + \alpha}

entropy inequality for classical Boltzmann

\forall \, f \in \mathcal{F}, \qquad D_{\delta}(f) \gtrsim H_{\delta}(f|M^f_{\delta})^{1 + \alpha}

entropy inequality for Boltzmann-Fermi-Dirac

\implies

known

new!

(Toscani, Villani)

transfer of inequalities

D_0(g) \gtrsim H_0(g|M_0^g)^{1 + \alpha}

D_{\delta}(f)

H_{\delta}(f|M_{\delta}^f)^{1 + \alpha}

we know:

D_{\delta}(f) \geqslant \kappa^{4} D_{0}\left(\frac{f}{1 - \delta f}\right)

\gtrsim \; \; D_{0}\left(\frac{f}{1 - \delta f}\right)

\gtrsim

entropy inequality for Boltzmann

Fermi-Dirac dissipation of \(f\)

\gtrsim \; \; H_0 \left(\frac{f}{1- \delta f} \left| M_0^{\frac{f}{1- \delta f}} \right. \right)^{1 + \alpha}

entropy inequality for Boltzmann-Fermi-Dirac

1 - \delta f \geq \kappa,

\kappa \in (0,1),

\left\{ \phantom{\begin{pmatrix} 0 \\ 0 \\ 0 \\ 0 \end{pmatrix}} \right.

1 / \delta

\kappa / \delta

we want:

Boltzmann dissipation of \( \displaystyle \frac{f}{1-\delta f} \)

\( \gtrsim\)

H_{\textcolor{green}{0}}\left(\left.\frac{f}{1 - \textcolor{purple}{\delta} f}\right|M^{\frac{f}{1 - \textcolor{purple}{\delta} f}}_{\textcolor{green}{0}}\right) \geqslant H_{\textcolor{purple}{\delta}}(f|M^f_{\textcolor{purple}{\delta}}).

whenever all terms make sense,

Boltzmann relative entropy to equilibrium of \(\displaystyle \frac{f}{1-\textcolor{purple}{\delta} f}\)

Fermi-Dirac relative entropy to equilibrium of \(f\)

Theorem.

[B.]

f \in L^1_2(\R^3)

\frac{f}{1 - \delta f} \in L^1_2(\R^3) \cap L \log L(\R^3),

\displaystyle 0 \leqslant f < \frac{1}{\delta}

For all

such that

and

\delta > 0

and

comparison of relative entropies

R_g : \delta \in \R_+ \mapsto H_{\delta}\left( \frac{g}{1 + \delta g} \left|M^{\frac{g}{1 + \delta g}}_{\delta} \right. \right).

Let

Then \(R_g\) is decreasing on \(\R_+\).

Proposition.

R_g(0) = H_{0}\left(\left.\frac{f}{1 - \delta f}\right|M^{\frac{f}{1 - \delta f}}_{0}\right)

g = \frac{f}{1 - \delta f},

R_g(\delta) = H_{\delta}(f|M^f_{\delta})

take

\geq

then

0 \leq g \in L^1_2(\R^3) \cap L \log L(\R^3)

and

\implies

Proof of the theorem

proof of the proposition

Key elements:

Taylor representation of the relative entropy to eq.
differentiation of \(R_g\) in \(\delta\)
general link between entropy and equilibrium
fact that \(x \mapsto -\left(\frac{x}{1+\delta x} \right)^2\) is decreasing

Other technicalities:

differentiability on \(\R_+^*\)
continuity at \(\delta = 0\)

general considerations

specific use of Fermi-Dirac features

\displaystyle H(f|M^f) = \int_0^1 (1-\tau) \int(f - M^f)^2 \, \Phi''(M^f + \tau (f-M^f)) \, \mathrm{d} v \, \mathrm{d} \tau

\(\displaystyle H(f) = \int \Phi(f) \, \mathrm{d} v\) with \(\Phi\) \(\mathcal{C}^2\) s.t. convex

\displaystyle H(f|M^f) = \int \, \int_{M^f(v)}^{f(v)} \, (f(v) - x) \, \Phi''(x) \, \mathrm{d} x \, \mathrm{d} v

Remark: suited to obtain general Cszisar-Kullback inequalities

M^f = (\Phi')^{-1} (\textcolor{blue}{\text{something conserved}})

Link between entropy and equilibrium

Taylor representation of relative entropy to equilibrium

entropy:

R_g : \delta \in \R_+ \mapsto H_{\delta}\left( \frac{g}{1 + \delta g} \left|M^{\frac{g}{1 + \delta g}}_{\delta} \right. \right).

Let

Then \(R_g\) is decreasing on \(\R_+\).

Proposition.

0 \leq g \in L^1_2(\R^3) \cap L \log L(\R^3)

and

Taylor representation of the relative entropy to eq.
differentiation of \(R_g\) in \(\delta\)
general link between entropy and equilibrium
fact that \(x \mapsto -\left(\frac{x}{1+\delta x} \right)^2\) is decreasing

<proof on the blackboard>

Proposition.

[B.]

0\leqslant f \in L^1_2(\R^3)

\displaystyle 1 - \delta f \geqslant \kappa,

For all

such that

\delta > 0, \;\; \kappa_0 \in (0,1)

and

Classical / Fermi-Dirac equivalence

H_{\textcolor{purple}{\delta}}(f|M^f_{\textcolor{purple}{\delta}}) \leqslant H_{\textcolor{green}{0}}\left(\left.\frac{f}{1 - \textcolor{purple}{\delta} f}\right|M^{\frac{f}{1 - \textcolor{purple}{\delta} f}}_{\textcolor{green}{0}}\right) \leqslant e^{ 16 \, \frac{1-\kappa}{\kappa} } \cdot H_{\textcolor{purple}{\delta}}(f|M^f_{\textcolor{purple}{\delta}})

D_{\textcolor{purple}{\delta}}(f) \leqslant D_{\textcolor{green}{0}}\left(\frac{f}{1 - \textcolor{purple}{\delta} f}\right) \leqslant \kappa^{-4} \cdot D_{\textcolor{purple}{\delta}}(f)

For Boltzmann (& Landau) equation:

entropy inequality for classical Boltzmann

entropy inequality for Boltzmann-Fermi-Dirac

1 - \delta f \geq \kappa_0

\iff

\delta f

\kappa

\Phi_0'' \circ(\Phi'_0)^{-1} \geqslant \Phi_1'' \circ(\Phi'_1)^{-1}

H_0(\varphi (f)|M_0^{\varphi(f)}) \leqslant H_1(f|M_1^{f})

\varphi = (\Phi_0')^{-1} \circ \Phi'_1

\leqslant

\geqslant

with

Perspective

conjecture:

then

Let \(\displaystyle H_0(f) = \int \Phi_0(f) \), \(\displaystyle H_1(f) = \int \Phi_1(f) \) with \(\Phi_0,\Phi_1\) \(\mathcal{C}^2\) s.t. convex.

D. Relaxation to equilibrium for Boltzmann-Fermi-Dirac

\|f^{\delta}_t-M_{\delta}\|_{L^p_k} \leq C \, (1+t)^{- \eta/p},

\(p \in [1,\infty), \, k \geq 0\), and with \(C,\eta\) explicit and uniform in \(\delta\).

Relaxation to equilibrium for Boltzmann-fermi-dirac

Theorem 1.

[B., Lods]

Let \(0\leqslant f^{\rm in} \in L^1_3(\R^3)\). Then \(\exists \delta^{\rm in} > 0\) such that \(\forall \delta \in (0,\delta^{\rm in})\), if \(f^{\delta} \) sol. to Boltzmann-Fermi-Dirac w/ cut-off hard potentials,

(\(\delta\) is the quantum parameter)

Proof's core ingredients:

\(L^{\infty}\)-bound on \(f^{\delta}\) independent of \(\delta\)
Entropy/entropy production inequality
Control of moments
Maxwellian lower-bound
Csiszar-Kullback-Pinsker inequality

1 - \delta f^{\delta} \geq \kappa

D_{\delta}(f_t^{\delta}) \geqslant C_t \; H_{\delta}(f_t^{\delta}|M^{f_t^{\delta}}_{\delta})^{1 + \alpha}

C_t \geqslant \widetilde{C}

\|f^{\delta}_t-M_{\delta}\|^2_{L^1_k} \leqslant C'\, H_{\delta}(f_t^{\delta}|M^{f_t^{\delta}}_{\delta})

\partial_t f_t^{\delta} = Q_{\delta} (f_t^{\delta}), \; \; f_0^{\delta} = f^{\rm in},

then

Proof's strategy:

\sup_{t \geq 0}\|f^{\delta}_t\|_{L^\infty} \leq \mathbf{C}^{\rm in}

the \(L^{\infty}\)-bound

Theorem 2.

[B., Lods]

Let \(0\leqslant f^{\rm in} \in L^1_3(\R^3)\). Then \(\exists \,\mathbf{C}^{\rm in} > 0\) such that \(\forall \delta> 0\), if \(f^{\delta} \) sol. to Boltzmann-Fermi-Dirac with cut-off hard potentials,

\delta \in (0, (1-\kappa) \mathbf{C}^{\rm in}) \; \; \implies \; \; 1 - \delta f^{\delta} \geq \kappa

Q_{\delta} \leqslant Q^+_0 + \widetilde{Q}^+_0 - Q^-_0

Q_{0} = Q^+_0 - Q^-_0

independent of \(\delta \)

\(f_t^{\delta}\) "sub-solution" to an eq. resembling classical Boltzmann

\(\widetilde{Q}^+_0\) "adjoint" to \(Q^+_0\)

(almost) copycat proof of same fact for classical Boltzmann

[Alonso, Gamba]

then

\partial_t f_t^{\delta} = Q_{\delta} (f_t^{\delta}), \; \; f_0^{\delta} = f^{\rm in},

overall recap

Monoatomic

Polyatomic

Resonant

Fermions

Entropy

Conserved quantities

Equilibrium

H(f) = \int \Phi_0(f)\\ \Phi_0' = \log

1 \\ v \\ |v|^2

v \mapsto

M(v) = \\ (\Phi_0')^{-1} (\textcolor{blue}{\alpha} \, 1 + \textcolor{blue}{\beta} \cdot v + \textcolor{blue}{\gamma} \,|v|^2)

1 \\ v \\ \frac12|v|^2 + \varepsilon(\zeta)

v, \zeta \mapsto

M(v,\zeta) = \\ (\Phi_0')^{-1} (\textcolor{blue}{\alpha} \, 1 + \textcolor{blue}{\beta} \cdot v + \textcolor{blue}{\gamma} ( \frac12|v|^2 + \varepsilon(\zeta)) )

1 \\ v \\ |v|^2 \\ I

v, I \mapsto

M(v,I) = \\ (\Phi_0')^{-1} (\textcolor{blue}{\alpha} \, 1 + \textcolor{blue}{\beta} \cdot v + \textcolor{blue}{\gamma_1} \, |v|^2 + \textcolor{blue}{\gamma_2} \, I)

H(f) = \int \Phi_{\delta}(f)\\ \Phi_{\delta}'(x) = \log \left( \frac{x}{1 - \delta x} \right)

1 \\ v \\ |v|^2

v \mapsto

M(v) = \\ (\Phi_{\delta}')^{-1} (\textcolor{blue}{\alpha} \, 1 + \textcolor{blue}{\beta} \cdot v + \textcolor{blue}{\gamma} \, |v|^2)

\psi_1, \psi_2, \dots, \psi_n

M = (\Phi')^{-1} \left( \sum_{i=1}^n \textcolor{blue}{\alpha_i} \, \psi_i \right)

Entropy

Equilibrium

Conserved quantities

\newcommand{\dd}{\mathrm{d}} H(f) = \int \Phi(f)

\newcommand{\dd}{\mathrm{d}} \Phi \; \; \mathcal{C}^2

st. convex

general link

Lagrange multipliers

Functional to minimize

constraints

Minimizer

perspectives

BONUS: general weighted \(L^p\) Csiszár-Kullback-Pinsker

General weighted \(L^p\) Csiszár-Kullback-Pinsker

\|f-M^f\|^2_{L^p_{\varpi}} \leqslant {\small C_{\Phi, \varpi, p, f, M^f}} \; H(f|M^f),

Proposition.

(general entropy)

with \(\displaystyle H(f) = \int\Phi(f)\), \(\Phi \; \; \mathcal{C}^2\) st. convex, \(M^f\) equilibrium, and

C_{\Phi, \varpi, p,f,M^f} = \left(\int_0^1 (1-\tau) \left\| \Phi''((1-\tau)M^f + \tau f)^{-1} \right\|_{L^{\frac{p}{2-p}}_{\varpi^2}}^{-1} \, \mathrm{d} \tau \right)^{-1}

For any \(f\), any \(p \in [1,2]\) and \(\varpi\) weight \(\geqslant 0\),

\|f-M_0^f\|^2_{L^p_{\varpi}} \leqslant 2 \max \left(\|f\|_{L^{\frac{p}{2-p}}_{\varpi^2}}, \|M_0^f\|_{L^{\frac{p}{2-p}}_{\varpi^2}} \right)\, H_{0}(f|M_0^f),

Corollary.

For any \(0\leq f \in L^1_2\cap L \log L(\R^3)\), \(p \in [1,2]\) and \(\varpi : \R^3 \to \R_+\),

(Boltzmann entropy)

with \(\displaystyle H_0(f) = \int f \log f\) and \(M_0^f\) Maxwellian.

[simplified]

[T. B.]

\(\mathrm{I}\). Boltzmann equation for polyatomic gases

\(\mathrm{II}\). Boltzmann equation for polyatomic gases with (quasi-)resonant collisions

\(\mathrm{III}\). Boltzmann-Fermi-Dirac equation

Bonus: weighted \(L^p\) Csiszar-Kullback-Pinsker inequalities

- General modelling framework

- Relationships between models

- Compactness result in resonant setting

- Modelling & study of quasi-resonant Boltzmann

- Entropy/entropy production inequalities via a transfer method

- Relaxation to equilibrium with explicit rate

w/ Lods

(Desvillettes)

w/ Bisi, Groppi

w/ Boudin, Mathiaud, Salvarani

(Boudin)

Thank you for your attention!

Première version soutenance pour backup

By Thomas Borsoni

Première version soutenance pour backup