Efficient and Optimal Fixed-Time Regret with Two Experts
Research Proficiency Exam
Victor Sanches Portella
PhD Student in Computer Science - UBC
October, 2020
The Two-Experts' Problem
Prediction with Expert Advice
Player
Adversary
\(n\) Experts
0.5
0.1
0.3
0.1
1
0
0.5
0.3
Probabilities
Costs
x_t
\ell_t
Player's loss:
\langle \ell_t, x_t \rangle
Goal: sublinear regret in the worst-case
\displaystyle
\mathrm{Regret}(T) = \sum_{t = 1}^T \langle \ell_t, x_t \rangle - \min_{i = 1, \dotsc, n} \sum_{t = 1}^T
\ell_t(i)
Known Results
Multiplicative Weights Update method:
\displaystyle
\mathrm{Regret}(T) \leq \sqrt{\frac{T}{2} \ln n}
Optimal for \(n,T \to \infty\) !
If \(n\) is fixed, we can do better
\(n = 2\)
\(n = 3\)
\(n = 4\)
\sqrt{\frac{T}{2\pi}} + O(1)
\sqrt{\frac{8T}{9\pi}} + O(\ln T)
\sim \sqrt{\frac{T \pi}{8}}
Player knows \(T\) !
Minmax regret in some cases:
What if \(T\) is not known?
\displaystyle
\frac{\gamma}{2} \sqrt{T}
Minmax regret
\(n = 2\)
[Harvey, Liaw, Perkins, Randhawa FOCS 2020]
They give an efficient algorithm!
\displaystyle
\gamma \approx 1.307
Known Results
Multiplicative Weights Update method:
\displaystyle
\mathrm{Regret}(T) \leq \sqrt{\frac{T}{2} \ln n}
Optimal for \(n,T \to \infty\) !
If \(n\) is fixed, we can do better
\sqrt{\frac{T}{2\pi}} + O(1)
Minmax regret for 2 experts:
[Harvey, Liaw, Perkins, Randhawa FOCS 2020]
\(O(1)\) time per round
[Cover '67]
Player knows \(T\) (fixed-time)
Player doesn't know \(T\) (anytime)
\displaystyle
\frac{\gamma}{2} \sqrt{T}
\displaystyle
\gamma \approx 1.307
\(O(T)\) time per round
Dynamic Programming
Stochastic Calculus
[Greenstreet]
Our results:
A complete theoretical analysis of the fixed-time algorithm
The case of 2 Experts
Player knows \(T\) (fixed-time)
Player doesn't know \(T\) (anytime)
\(O(1)\) time per round
\(O(T)\) time per round
Stochastic calculus and discretization techniques
Dynamic programming
?
[Greenstreet]
\(O(1)\) time per round
[Harvey et al. '20]
\frac{\gamma}{2} \sqrt{T}
minmax regret
\sqrt{\frac{T}{2\pi}} + O(1)
minmax regret
[Cover '67]
Our results:
An efficient and optimal algorithm for two experts
regret
\sqrt{\frac{T}{2\pi}} + O(1)
Gaps and Cover's Algorithm
Binary costs
We will consider only 0 or 1 costs (no fractional costs!) Enough for the worst case
1
0
0
1
0
0
1
1
Equal costs are a "waste of time", so we do not consider those
Cover's algorithm strongly relies on these assumptions
Gap between experts
Thought experiment: how much probability mass to put on each expert?
Cumulative Loss on round \(t\)
\(\frac{1}{2}\) is both cases seems reasonable!
Takeaway: player's decision could depend on the gap between experts
Gap = |42 - 20| = 22
Lagging Expert
Leading Expert
42
20
2
2
42
42
Cover's Dynamic Program
Path-independent player:
Choice on round \(t\) depends only on the gap \(g_{t-1}\) of round \(t-1\)
Choice doesn't depend on the specific past costs
Path-independent player \(\implies\)
\(V_p[t,g]\) depends only on \(\ell_{t+1}, \dotsc, \ell_T\) and \(g_t, \dotsc, g_{T}\)
\displaystyle
V_p[0, 0] =
Maximum regret of \(p\)
p(t, g_{t-1})
on the Lagging expert
1 - p(t, g_{t-1})
on the Leading expert
We can compute \(V_p\) backwards in time!
We then choose \(p^*\) that minimizes \(V^*[0,0] = V_{p^*}[0,0]\)
\displaystyle
V_p[t, g] =
Maximum regret-to-be-suffered on rounds \(t+1, \dotsc, T\) if gap at round \(t\) is \(g\)
Regret and Player in terms of the Gap
Path-independent player:
If
round \(t\) and gap \(g_{t-1}\) on round \(t-1\)
p(t, g_{t-1})
1 - p(t, g_{t-1})
on the Lagging expert
on the Leading expert
Choice doesn't depend on the specific past costs
p(t, 0) = 1/2
for all \(t\), then
\displaystyle
\mathrm{Regret(T)}
= \sum_{t = 1}^{T}
p(t, g_{t-1})(g_t - g_{t-1})
gap on round \(t\)
A discrete analogue of a Riemann-Stieltjes integral
A formula for the regret
A Dynamic Programming View
\displaystyle
V_p[t, g] =
Maximum regret-to-be-suffered on rounds \(t+1, \dotsc, T\) when gap on round \(t\) is \(g\)
Path-independent player \(\implies\) \(V_p[t,g]\) depends only on \(\ell_{t+1}, \dotsc, \ell_T\) and \(g_t, \dotsc, g_{T}\)
\displaystyle
V_p[t, 0] = \max\{p(t+1,0), 1 - p(t+1,0)\} + V_p[t+1, 1]
Regret suffered on round \(t+1\)
Regret suffered on round \(t + 1\)
\displaystyle
V_p[t, g] = \max \Bigg\{
\displaystyle
V_p[t+1, g+1] + p(t + 1,g)
\displaystyle
V_p[t+1, g-1] - p(t + 1,g)
A Dynamic Programming View
\displaystyle
V_p[t, g] =
Maximum regret-to-be-suffered on rounds \(t+1, \dotsc, T\) if gap at round \(t\) is \(g\)
We can compute \(V_p\) backwards in time!
Path-independent player \(\implies\)
\(V_p[t,g]\) depends only on \(\ell_{t+1}, \dotsc, \ell_T\) and \(g_t, \dotsc, g_{T}\)
We then choose \(p^*\) that minimizes \(V^*[0,0] = V_{p^*}[0,0]\)
\displaystyle
V_p[0, 0] =
Maximum regret of \(p\)
A Dynamic Programming View
For \(g > 0\)
\displaystyle
p^*(t,g) = \frac{1}{2}(V_{p^*}[t, g-1] - V_{p^*}[t, g + 1])
Optimal player
\displaystyle
p^*(t,0) = \frac{1}{2}
Optimal regret (\(V^* = V_{p^*}\))
\displaystyle
V^*[t,g] = \frac{1}{2}(V^*[t+1, g-1] + V^*[t+1, g + 1])
For \(g = 0\)
\displaystyle
V^*[t,0] = \frac{1}{2} + V^*[t+1, 1]
For \(g > 0\)
For \(g = 0\)
A Dynamic Programming View
Optimal regret (\(V^* = V_{p^*}\))
\displaystyle
V^*[t,g] = \frac{1}{2}(V^*[t+1, g-1] + V^*[t+1, g + 1])
\displaystyle
V^*(t,0) = \frac{1}{2} + V^*[t+1, 1]
For \(g > 0\)
For \(g = 0\)
g
t
4
3
2
1
0
0
0
0
0
0
0
0
\frac{1}{2}
0
0
0
0
0
0
0
0
0
0
0
0
0
1
2
3
Connection to Random Walks
\displaystyle
V^*[0,0] =
Maximum regret of \(p^*\)
Theorem
\displaystyle
V^*[0,0] =
Expected # of 0's of a Sym. Random Walk of Length \(T\)
\displaystyle
\frac{1}{2}
\displaystyle
\Big(
\displaystyle
\Big)
\displaystyle
[\tfrac{2}{5}, 1] + \sqrt{\frac{2T}{\pi}} =
Theorem
For any player, if the gaps are random and distributed like a reflected symmetric random walk,
\displaystyle
\mathbb{E}[\mathrm{Regret}(T)] \geq
Expected # of 0's of a SRW of Length \(T - 1\)
\displaystyle
\frac{1}{2}
\displaystyle
\Big(
\displaystyle
\Big)
Continuous Regret
A Probabilistic View of Regret Bounds
Formula for the regret based on the gaps
\displaystyle
\mathrm{Regret(T)}
= \sum_{t = 1}^{T}
p(t, g_{t-1})(g_t - g_{t-1})
Discrete stochastic integral of \(p\) with respect to the reflected RW \(g\)
Moving to continuous time:
Random walk \(\longrightarrow\) Brownian Motion
Insight:
Regret bound \(\equiv\) almost sure bound on the integral
Gaps are on the support of a reflected random walk
A Probabilistic View of Regret Bounds
Formula for the regret based on the gaps
\displaystyle
\mathrm{Regret(T)}
= \sum_{t = 1}^{T}
p(t, g_{t-1})(g_t - g_{t-1})
Random walk \(\longrightarrow\) Brownian Motion
\displaystyle
\mathrm{ContRegret(p, T)}
= \int_{0}^{T}
p(t, |B_t|)\mathrm{d}|B_t|
Reflected Brownian motion
Conditions on the continuous player \(p\)
Continuous on \([0,T) \times \mathbb{R}\)
p(t,0) = \frac{1}{2}
for all \(t \geq 0\)
Stochastic Integrals and Itô's Formula
How to work with stochastic integrals?
\displaystyle
f(T, |B_T|) - f(0, |B_0|) = \int_{0}^T \partial_g f(t, |B_t|) \mathrm{d}|B_t| + \int_{0}^T \overset{*}{\Delta} f(s, |B_s|) \mathrm{d}s
Itô's Formula:
\displaystyle
\overset{*}{\Delta} f(s, |B_s|)
= \partial_t f(s, |B_s|) + \frac{1}{2} \partial_{gg} f(s, |B_s|)
\displaystyle
\mathrm{ContRegret}(\partial_g f, T)
Different from classic FTC!
\(\overset{*}{\Delta} f(t, g) = 0\) everywhere
ContRegret doesn't depend on the path of \(B_t\)
\displaystyle
\implies
Backwards Heat Equation
Goal:
Find a "potential function" \(R\) such that
(1) \(p = \partial_g R\) is a valid continuous player
(2) \(R\) satisfies the Backwards Heat Equation
A Solution Inspired by Cover's Algorithm
For Cover's algorithm, we can show
p^*(t,g) =
Lagging expert finishes leading
\mathbb{P} \Bigg(
\Bigg)
Gaps ~ Reflected RW
Law of Large Numbers:
\displaystyle
= \mathbb{P}\Big(\mathcal{N}(0,T - t) > g\Big)
\displaystyle
\Big\} \eqqcolon Q
= \mathbb{P}(S_T > 0 | S_t = -g)
Itô's Formula \(\implies\)
\displaystyle
\mathrm{ContRegret}(Q, T) \leq
\displaystyle
\sqrt{\frac{T}{2\pi}}
\displaystyle
\approx \mathbb{P}(B_T > 0 | B_t = -g)
\(Q\) satisfies BHE
\(R(t,g)\) such that
\implies
Calculus trick
\displaystyle
\Bigg\{
\(R\) satisfies BHE
\(\partial_g R = Q\)
\(R(t,g) \leq \sqrt{T/2\pi}\)
But we wanted a potential R satisfying BHE
Discretization
Discrete Derivatives
p^*(t,g) = \frac{1}{2} \big( V^*[t, g-1] - V^*[t, g+1]\big)
\approx \partial_g V^*[t,g]
\eqqcolon V_g^*[t,g]
V^*[t, g] - V^*[t-1, g]
= \frac{1}{2}( V^*[t, g-1] - V^*[t, g]) - \frac{1}{2}(V^*[t, g] - V^*[t,g+1])
\coloneqq V_t^*[t,g]
\coloneqq \frac{1}{2}V_{gg}^*[t,g]
\partial_t V^*[t,g] \approx
\approx \frac{1}{2}\partial_g V^*[t,g-1]
\approx \frac{1}{2} \partial_g V^*[t,g]
\approx \frac{1}{2} \partial_{gg} V^*[t,g]
Discrete Derivatives
p^*(t,g) = \frac{1}{2} \big( V^*[t, g-1] - V^*[t, g+1]\big)
\approx \partial_g V^*[t,g]
\eqqcolon V_g^*[t,g]
V^*[t, g] - V^*[t-1, g]
= \frac{1}{2}( V^*[t, g-1] + V^*[t, g+1] - 2V^*[t,g])
\coloneqq V_t^*[t,g]
\coloneqq \frac{1}{2} V_{gg}^*[t,g]
\(V^*\) satisfies the "discrete" Backwards Heat Equation!
Discretizatized player:
q(t,g) \coloneqq R_g(t,g)
Bound regret with a discrete analogue of Itô's Formula
Hopefully, \(R\) satisfies the discrete BHE
Bounding the Discretization Error
In the work of Harvey et al., they had
R_t(t,g) + \tfrac{1}{2} R_{gg}(t,g) \geq 0
In this fixed-time solution, we are not as lucky
Negative discretization error!
g
t
T = 1000
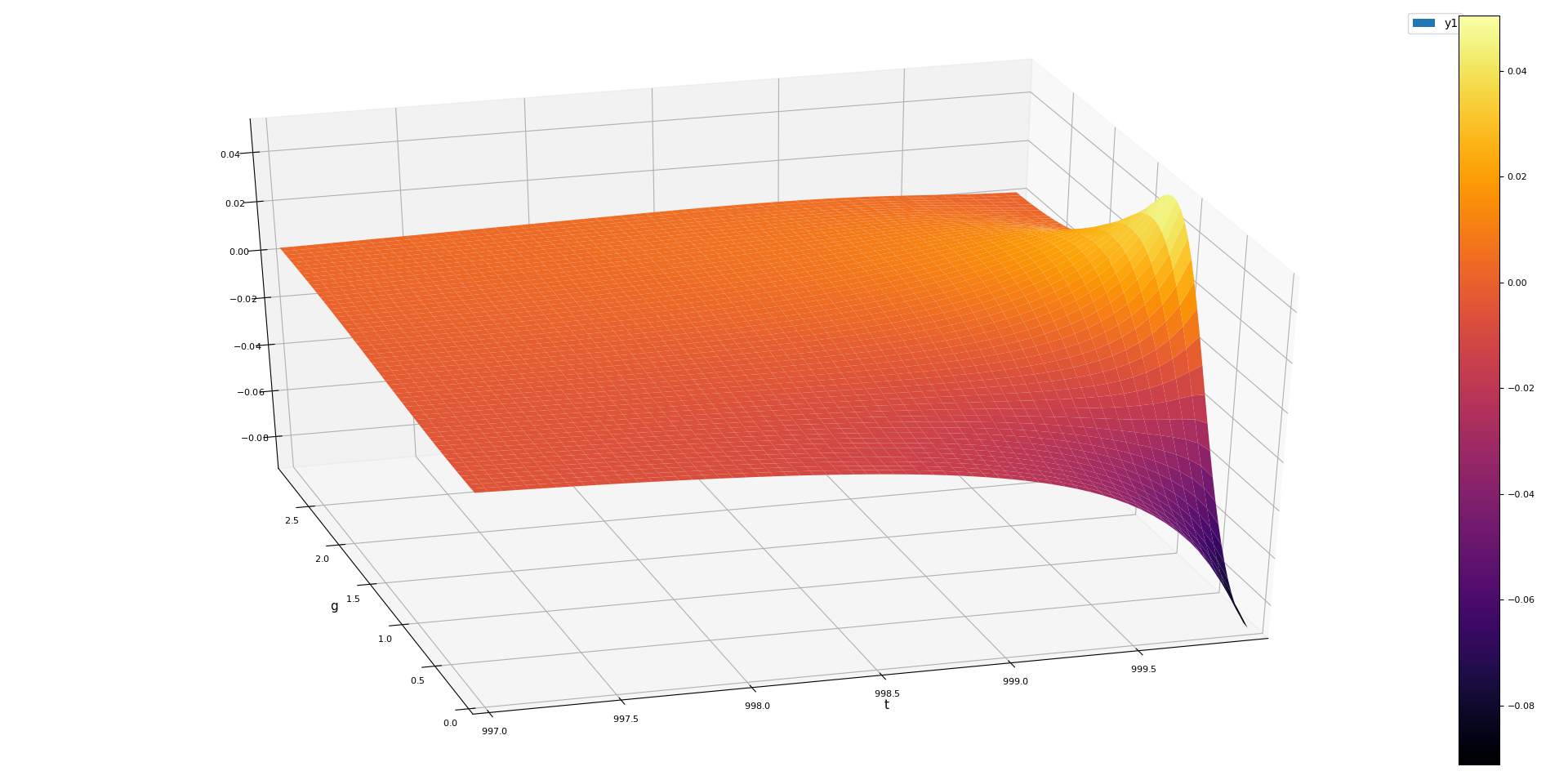
Bounding the Discretization Error
Main idea
\(R\) satisfies the continuous BHE
\implies
R_t(t,g) + \frac{1}{2} R_{gg}(t,g) \approx
Approximation error of the derivatives
\implies
\leq 0.74
\displaystyle
\mathrm{Regret(T)} \leq \frac{1}{2} + \sqrt{\frac{T}{2\pi}} + \sum_{t = 1}^T O\Bigg( \frac{1}{(T - t)^{3/2}}\Bigg)
Lemma
\partial_{gg}R(t,g) - R_{gg}(t,g)
\partial_t R(t,g) - R_t(t,g)
\in O\Big( \frac{1}{(T - t)^{3/2}}\Big)
\Bigg\}
Efficient and Optimal Fixed-Time Regret with Two Experts
Research Proficiency Exam
Victor Sanches Portella
PhD Student in Computer Science - UBC
October, 2020
RPE Presentation
By Victor Sanches Portella
